近物面爆炸气泡溃灭与射流载荷特性研究
古 滨, 刘亮涛, 魏铭利, 邱清水, 姚熊亮, 王志凯
(1.西华大学土木建筑与环境学院, 成都 610039;2.哈尔滨工程大学船舶工程学院, 哈尔滨 150001)
引 言
水下爆炸指炸药、鱼雷、炸弹或核弹等在水中的爆炸。爆炸后在水中形成向四周扩展并不断减弱的冲击波。爆炸产物形成的气泡在水中膨胀,然后回缩,进行振荡并不断上浮,同时向四周发出二次压力脉冲。当冲击波遇到物体时发生反射、折射和绕射,物体在冲击波和二次压力脉冲的作用下发生位移、变形或破坏。冲击波到达水面和气球突出水面后,在水面激起表面波。水下爆炸已有了较为系统的研究,并取得了较丰硕的成果,如古滨等[1-2]通过ALE方法结合数值模拟研究了水下冲击波作用下双层壳结构的响应特征,姜忠涛等[3]研究了近场水下爆炸气泡射流载荷冲击船体外板的动响应。
水下气泡在不同边界条件附近会呈现出不同的运动特性,由于气泡周围边界条件的不对称,会使气泡周围压力分布朝某个方向产生梯度,在坍塌过程中气泡将会朝压力梯度大的方向产生射流,并穿透气泡。根据边界类型的不同,射流产生的方向会发生改变,如在自由液面附近,射流远离自由液面,而壁面附近的气泡将会朝向壁面产生射流,这种射流现象最早由Naude和Ellis(1961)[4]、Benjamin和Ellis(1966)[5]等在实验中观测到,并被认为是结构空化剥蚀的主要原因。对于近物面的气泡,除了距离对气泡运动特性影响显著之外,初始参数的不同,气泡的运动形式和射流载荷特性也会呈现出不同的特征。对于爆炸气泡等尺度较大的气泡,浮力对气泡的作用较为显著。而对于空化等尺度较小的气泡,粘性对气泡的作用逐渐凸显。对于存在自由液面影响的气泡,由于物面和自由液面的耦合作用,气泡射流又会有不一样的表现形式。
尽管气泡在不同边界附近的运动特性已经被很多学者深入地研究,如王加夏等[6]通过电火花气泡装置和高速摄像设备对气泡与附近刚性/柔性边界间的耦合现象进行了实验观测和研究;贺铭等[7]利用欧拉有限元数值模型对近场水下爆炸气泡与双层破口结构的相互作用机理进行了研究,主要分析了舱室涌流及流场演化等物理属性;李梅[8]等研究了双爆源气泡与水面的相互作用过程;朱锡、张阿漫等[9-13]都开展过小当量真实装药水下爆炸产生气泡的实验,研究气泡脉动周期和最大半径等参数,得到了气泡全周期的运动形态。但是,由于很多方面的局限性,目前对于近物面,尤其一些极近物面不同参数下的气泡坍塌运动和射流载荷特性的研究并不系统。
为此,本文基于不可压缩流体控制方程建立气泡脉动及射流载荷特性的计算模型。通过分析不同物面深度下射流特征参数分别与药包质量和无量纲距离参数的变化趋势,开展了考虑水下爆炸气泡射流速度、射流宽度和射流高度等方面的较为系统的研究,基于数值模拟与模型实验相结合的方法,验证了计算方法的有效性,并提出了3种有效的数值预报模型。
1 计算模型
1.1控制方程
假设流体绝热,气泡内部和外界流场不存在质量和热交换。气泡在外界流场的速度在大部分时间内都要远小于声速,因此外界流场的可压缩性忽略不计。气泡运动之前,假设流体静止,随后气泡的运动被认为是轴对称的,如图1所示,因此流体的运动由不可压缩、粘性的Navier-Stokes方程控制,柱坐标下的Navier-Stokes方程有如下表现形式:
(1)
(2)
(3)
式中,
其中:x和y分别为轴对称坐标轴r和z;u和v分别表示坐标轴x和y方向的速度;ρ1表示流体密度;p表示流体压力;gy表示沿y方向的重力加速度;υ表示运动粘性系数。当式(1)~式(3)中的粘性项不考虑时,方程变为不可压缩Euler方程。

图1 轴对称坐标示意图
1.2气体状态方程
如果直接采用流体控制方程求解气泡内部可压气体和外部不可压液体,界面处的数值不稳定将是个巨大的挑战。为了避免出现这种情况,通常假设气泡内部压力均匀分布,把压力作为外界流场的压力边界条件。这种假设对气泡的运动影响较小,因此是合理的,此时气泡内部的气体的状态可以用理想气体状态方程表示。气泡内部压力由常值蒸汽压力和随体积变化的非冷凝气体压力组成,根据绝热假设,气泡内部的理想气体状态方程可以转化成另一种表现形式:
(4)
其中:pb表示气泡内部压力;pv表示饱和蒸汽压力;p0表示气泡初始压强;V0对应的非冷凝气体压力;Vt表示气泡在任一时刻的体积;ϑ表示气体的比热。
1.3边界条件
在求解气泡外界流场之前,需要确定流场的边界条件。垂直于对称轴和刚性壁面的速度分量满足不可穿透条件,可以写成:
v·n=0
(5)
其中,v表示流场的速度矢量,n表示边界指向流场的单位法向速度。
无穷远处的压力边界条件由静水压力表示:
pout=p
(6)
其中,pout表示无穷远处的静水压力。
由于气泡内部气体的运动状态不予以直接求解,因此需要把压力当成外界流场的压力边界条件。在气泡界面处,切向压力条件和法向压力条件需要同时满足。由于气泡内部气体的粘性极小,通常忽略不计,因此切向压力边界条件可以写成:
μ·τ·δ·n=0
(7)
其中:τ表示界面的单位切向量;δ表示偏应力张量。
法向压力边界条件需要满足:
(8)
其中,pl表示在外界流场一侧边界处的压力,σ表示表面张力系数;κ表示气泡表面的局部曲率,可以通过Young-Laplace方程进行求解:
(9)
其中,R1和R2分别表示沿x和y轴的主曲率半径。对于轴对称模型气泡表面质点的位置x(s)和y(s)可以当成弧长s的函数,因此主曲率半径R1和R2可以表示成:
(10)
(11)
2 计算结果验证与分析
2.1气泡溃灭运动过程验证
实验验证的工况见表1。这里采用相同的工况对边界积分方程进行理论验证,理论验证主要将边界积分方程计算的结果和Rayleigh-Plesset方程的理论值进行对比,包括半径曲线和气泡表面节点速度。在这之前,先对边界积分方程进行收敛性验证,确定气泡表面节点数量N和Δφ速度势变化值。气泡的初始半径R0=0.0204,初始内部压力P0=66.928 MPa。图2给出了不同速度势变化值Δφ下的气泡射流时历曲线。当Δφ取值较大时,射流速度不稳定,出现明显的振荡现象。当Δφ取值减小时,射流速度逐渐收敛。当Δφ等于0.01时,射流速度基本收敛。因此在随后的计算中,将速度势变化值Δφ取为0.01。图3中给出了气泡表面不同节点数量的射流速度收敛曲线,当节点速度大于60时基本收敛,随后的计算将节点数量N取为60。图4和图5分别给出边界积分方程数值解和Rayleigh-Plesset方程理论解两者关于气泡表面节点速度和气泡半径的对比曲线。由图4和图5可见,无论是节点速度曲线还是半径曲线,边界积分方程的数值结果和理论解都吻合得较好。

表1水下爆炸实验初始参数

图2 速度势变化值Δφ收敛性分析
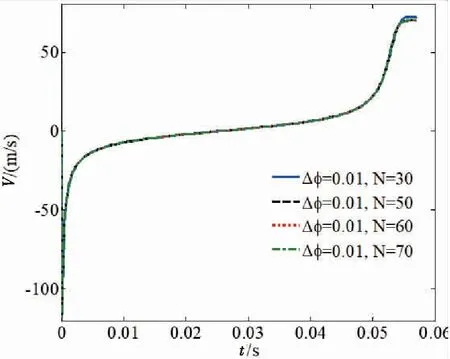
图3 气泡表面节点数量收敛性分析

图4 边界积分方程数值解和理论解关于气泡节点速度对比
采用边界积分方程模拟的数值结果与实验对比情况如图6所示,数值结果中的箭头表示速度方向,云图表示流场压力。由图6可知,除了环状阶段的凸起,数值结果与实验结果吻合良好。由于凸起主要由气液混合组成,里面包含了很多破碎的小气泡,因此很难采用边界积分方程对气液混合物进行模拟,通常在计算过程中会忽略不计。因此采用边界积分方程来研究水下爆炸气泡射流特征参数是合适的。

图5 边界积分方程数值解和理论解关于气泡半径对比

图6 水下爆炸气泡数值与实验对比
2.2气泡射流载荷计算
2.2.1 射流速度模型
气泡射流与无量纲距离参数的关系可以采用多项式来表示,通过比较一系列不同的数学模型,最后选用以下数学模型来描述射流速度V与药包质量和无量纲距离参数之间的关系:
(12)
其中,ai(i=1,2,3,4,5)表示未知系数。不同物面深度下未知系数ai的取值情况见表2。

表2不同物面深度下的射流速度系数
图7给出了物面深度等于50 m和250 m时射流速度数学模型与边界元数值结果的整体对比。从图中可以看出,边界元数值结果散落在射流速度数学模型周围,通过计算,两者之间的最大误差不超过2%。

图7 射流速度数学模型与边界元数值结果的整体对比
为了进一步验证式(12)中的射流速度数学模型和表2中系数的准确性,对射流速度数学模型与边界元数值结果的进行局部对比分析。图8给出了物面深度h等于50 m和250 m时射流速度数学模型与边界元数值结果随着药包质量变化的局部对比,其中无量纲距离参数分别等于0.65、1.0和1.5。无论从曲线的变化趋势上,还是从结果的吻合程度上来看,射流速度数学模型在药包质量这个变化方向上的结果和边界元数值结果吻合较为一致。图9给出了物面深度h=50 m和250 m时射流速度数学模型与边界元数值结果随着无量纲距离参数变化的局部对比,其中药包质量W分别等于50 kg, 500 kg和1000 kg。从图9中可以看出,边界元的数值结果与射流速度数学模型计算的结果吻合较为一致。即使射流速度在无量纲距离参数γ=0.7存在拐点,射流速度数学模型也能对边界元数值结果进行完美表示,如图9(b)所示。

图8 射流速度数学模型与边界元数值结果随着药包质量变化的局部对比

图9 射流速度数学模型与边界元数值结果随着无量纲距离参数变化的局部对比
2.2.2 射流宽度模型
射流宽度与无量纲距离参数的关系采用多项式进行表示。通过对多种数学函数模型进行比较,选取以下数学模型来描述射流宽度D与药包质量和无量纲距离参数之间的关系:
肉牛养殖中,胃肠道疾病是十分常见的一类疾病。引起肉牛胃肠道疾病的致病原因多样,包括致病原因和饲养管理。在具体诊治中,应该结合肉牛临床症状,明确致病原因,采取针对性措施进行治疗,避免随意用药,增加药物耐药性,降低治疗效果。
(13)
其中,ai(i=1,2,3,4,5)表示未知系数。不同物面深度下未知系数ai的取值情况见表3。
图10给出了物面深度分别等于50 m和250 m时,射流宽度数学模型与边界元数值结果的整体对比。从两者相对位置来看,边界元数值结果的散点几乎都座落在数学模型曲面上,最大误差只有1.4%。可见,射流宽度数学模型结合相应的物面深度系数能较精确地表示射流宽度。
通过图10中数学模型曲面上颜色的分布情况,能很直观地反映出射流宽度随着药包质量和无量纲距离参数的变化趋势。射流宽度沿着无量纲距离参数这个方向的变化不是很明显,较大的射流宽分布在药包质量较大的红色区域。

表3不同物面深度下的射流宽度系数

图10 射流宽度数学模型与边界元数值结果的整体对比
2.2.3 射流高度模型
射流高度与无量纲距离参数的关系也采用多项式进行描述。通过多个函数对比和筛选,选择以下数学模型来描述射流高度L与药包质量和无量纲距离参数之间的关系:
(14)
其中,ai(i=1,2,3,4,5)表示未知系数。不同物面深度下未知系数ai的取值情况见表4。

表4不同物面深度下的射流高度系数
图11给出了物面深度分别等于50 m和250 m时,射流高度数学模型与边界元数值结果沿着药包质量和无量纲距离参数这两个方向的整体对比情况。从图11可以看出,射流高度数学模型的曲面结果和边界元数值结果吻合得较为一致,通过分析,两者之间最大误差不超过3.1%。通过射流高度数学模型曲面颜色的分布情况,能很直观的看出射流高度随着药包质量和无量纲距离参数的变化趋势。随着药包质量的增加,每一药包质量下对应的最大射流高度逐渐朝着无量纲距离参数增大方向偏移。

图11 时射流高度数学模型与边界元数值结果的整体对比
2.2.4 射流载荷模型
由于气泡射流载荷的复杂性,目前关于气泡射流载荷的表现形式并没有明确的定论。但是,国内外关于水射流的砰击特性却做了较为系统的研究,并取得了较丰硕的成果[14-16],因此这一节将在射流速度数学模型、射流宽度数学模型、射流高度数学模型和水射流理论的基础上,研究描述射流载荷变化趋势的数学模型,旨在为近物面水下爆炸气泡射流载荷工程预报提供一定的指导。
当水射流以较高的速度砰击到结构表面时,由于速度较快,流体会被瞬间压缩产生冲击波,如图12所示,因此高速水射流砰击平板那一瞬时的压力通常认为是水锤压力。在一维假设下,基于可压缩流体力学的质量和动量定理,水射流作用在刚性板表面时,在砰击区域中心点处的初始压力Pm可以表示如下:
Pm=ρ1cV
(15)
其中:ρ1表示流体密度;c表示冲击波传播速度;V表示水射流速度。

图12 水射流砰击过程
水锤压力持续的时间很短,其持续的时间为稀疏波从水射流边界传播到中心的时间(图12),因此水锤压力作用的时间τ可以表示为:
(16)
其中,D为水射流宽度。
水锤压力释放之后,砰击区域中心点处的压力逐渐趋于稳定,即进入驻压阶段(图12),该阶段的水动压力大小为:
(17)
当考虑材料变形对水射流砰击的影响时,需要对公式(15)中的压力进行修正,修正后砰击区域中心点处的初始压力可以表示为:
(18)
其中:ρ1和ρ2表示流体和材料的密度;c1和c2表示冲击波在流体和材料中的传播速度。
图13给出较典型的水射流以570 m/s冲击平板时中心点处的压力曲线。压力曲线的峰值压力为850 MPa,数值与实验水锤压力几乎相等(未超过10%)。水锤压力持续的时间约为1 μs与式(16)计算的较为一致,这里水射流的宽度为3 mm。随后,压力进入驻压阶段,该阶段的压力约为式(17)计算的压力值。接下来,在图13水射流实验载荷的基础上,建立水射流载荷数学模型。通过对实验数据分析可知,稀疏波从水射流边缘传播到中心这个阶段,水锤压力主要以指数形式进行衰减,而在稳态阶段,压力趋于平稳,因此建立以下数学模型来描述水射流载荷的变化趋势:
P=Aexp(-Bt)+C
(19)
其中:A,B和C为未知系数;通过初始时刻压力峰值Pm,τ时刻的压力Pτ和无穷远时刻的压力Pe可以对未知系数进行求解,然后再将系数代入就可以得到水射流载荷随时间变化的表达式:
(20)


图13 水射流载荷数学模型与实验数据对比
3 结束语
针对水下爆炸气泡射流速度、射流高度、射流宽度和射流载荷缺乏系统性研究的这一问题,本文基于边界积分方程研究了水下爆炸气泡射流特性与药包质量、无量纲距离参数和物面深度之间的关系。通过分析不同物面深度下射流特征参数分别与药包质量和无量纲距离参数的变化趋势,建立了射流速度、射流宽度和射流高度3种数学模型,并验证了它们的有效性。爆炸气泡射流速度随着药包质量的增加而减小,变化趋势符合幂函数Wa(0

