协调接触微动面裂纹萌生位置研究*
王 军,刘 勇
(中北大学 能源动力工程学院,山西 太原 030051)
0 引言
机械结构在交变载荷作用下,接触表面间发生微米量级的相对运动称为微动。微动现象普遍存在于连接件、紧固件和夹持机构之间[1-2]。微动会造成接触表面的损伤,进而会引起零件疲劳。研究表明,微动损伤对各种机械装置危害巨大,微动会使材料疲劳极限降低20%~50%,最高可达80%[3]。微动根据接触形式分为两大类,协调接触(面接触)微动和非协调接触(点接触、线接触)微动。由于非协调接触压头的接触状态相对更为明确,接触应力更容易获得,在微动的研究中应用较多。对于协调接触,由于压头与试件间不易获得严格意义上的面-面接触,接触压力的分布难以精确控制,因而研究相对较少。但实际零件在工作中更多地是处于面-面协调接触状态,而且协调接触结构接触边缘的奇异应力分布导致比非协调接触条件下更容易产生微动疲劳裂纹[4],对其进行实验及理论研究具有更强的工程实用价值。
作者前期已经通过对亚共晶铝硅合金ZL702A微动疲劳试验研究,对协调接触条件下材料的微动疲劳性能、微动区擦痕、断面等进行了现象分析[5]。微动接触表面的应力分布是引发微动疲劳的重要因素,是研究微动机理需要明确的关键参数。但由于接触表面的应力梯度很大,应变片无法精确测定应变,接触表面间仅有几十微米的相对滑移量,而且接触表面封闭在试件与压头之间,在现有试验条件下很难对微动区复杂的应力状态和相对滑移量进行精确测量。为了更好地理解协调接触条件下材料的微动疲劳机理,本文使用接触非线性有限元分析方法建立了协调接触微动疲劳仿真模型,对试验条件下微动区的应力响应特征、断裂位置以及轴向载荷、法向载荷等因素对微动滑移量的影响进行研究。
1 协调接触有限元分析模型的建立
协调接触微动试验中试件与压头的结构及配合关系如图1(a)所示。考虑到结构属于双对称条件,建立1/4平面有限元模型(如图1(b)所示)对微动疲劳时试件的应力分布进行仿真。对应分析试件的矩形L×B中,L=4B=20 mm,微动压头半宽a=4 mm,接触面到微动压头施加载荷位置的距离h=2 mm。使用二维4节点平面应变四边形完全积分单元(Plane182)剖分网格,试件与压头接触处(即微动接触面)剖分规则的10 μm×10 μm细网格(如图1(c)所示),远离接触区域网格数量逐步减少。最后得到有限元模型的节点数28 198个、单元数27 934个。微动压头与试件之间的接触使用ANSYS软件接触面-目标面规则进行定义,压头的下表面定义为接触面(Conta172单元),试件的上表面定义为目标面(Target169单元),接触面节点与目标面节点成对出现,形成接触对。试件使用亚共晶铝合金ZL702A,弹性模量69 GPa,泊松比0.31,压头使用合金钢42 CrMo,弹性模量206 GPa,泊松比0.28。通过两个载荷步按顺序施加载荷,在第一个载荷步在压头上施加2 kN法向力P使微动压头与试件表面保持p=62.5 MPa名义接触压力,第二个载荷施加循环载荷中的最大轴向应力σ=69.17 MPa。建模时网格剖分、载荷及约束施加在有限元前处理软件ANSA中进行,计算及后处理在有限元软件ANSYS中完成。
2 结果及分析
2.1 应力分布特征
试件剪应力、切向应力、法向应力和等效应力分布分别如图2、图3、图4和图5所示。图中对试件微动面及靠近微动面区域处应力云图按图1(b)所定义坐标系进行了长度标注,x轴从0到4 mm范围对应试件的微动接触面区域。
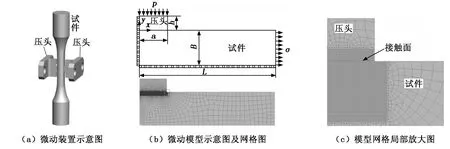
图1 微动疲劳模型

图2 压头与试件剪应力分布
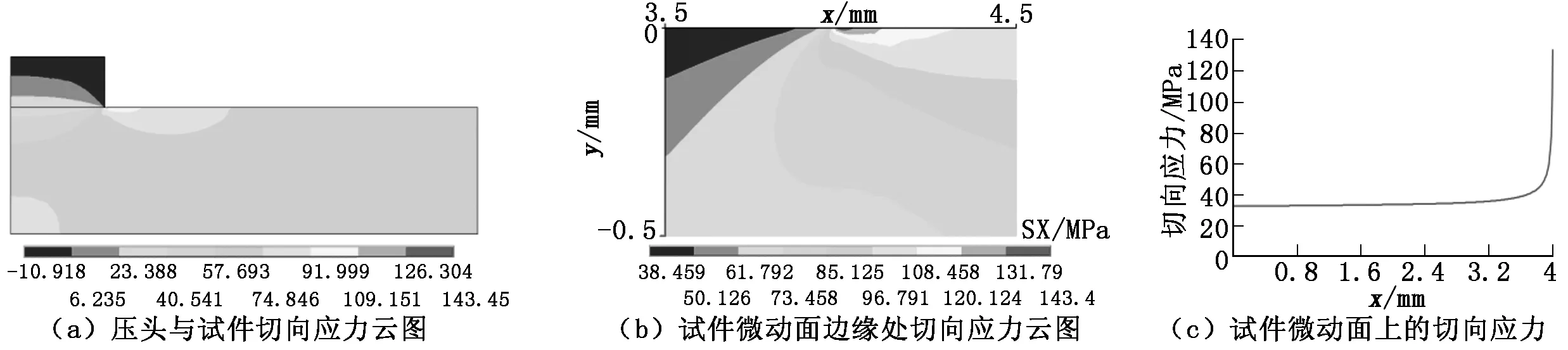
图3 压头与试件切向应力分布
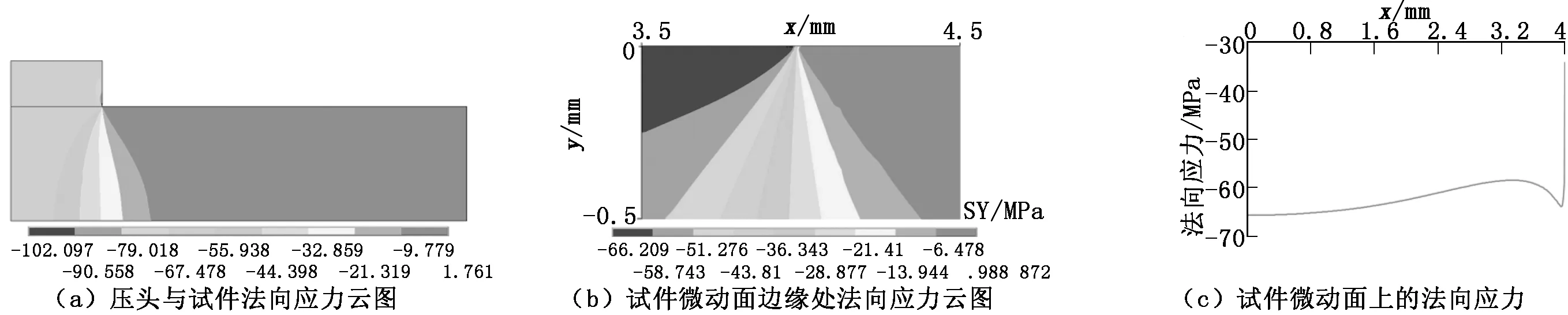
图4 压头与试件法向应力分布

图5 压头与试件等效应力分布
图2表明:试件表面剪应力从接触中心(x=0 mm)到边缘逐渐增大,在试件距微动区边缘0.2 mm处达到最大,为-21.6 MPa,然后迅速减小;在试件内部,剪应力最大为13.2 MPa,位于试件接触边缘正下方约2 mm深度位置。图3表明:试件表面从0到3.6 mm范围,切向应力基本保持在40 MPa左右;在距微动区边缘约0.4 mm处切向应力开始明显变大,到微动区边缘处(x=4 mm)达到最大,为143.5 MPa。图4表明:试件表面从接触中心到3.8 mm范围,法向应力先缓慢减小,然后又增大,但整体在-65 MPa到-60 MPa范围波动,即在名义法向压力62.5 MPa左右波动;从3.8 mm开始法向应力开始明显减小,到微动区边缘处(x=4 mm)达到最小,为36.5 MPa。图5表明:试件表面从接触中心到3.6 mm范围,等效应力基本保持在85 MPa左右;在试件表面距微动区边缘约0.4 mm处等效应力开始明显变大,到微动区边缘处(x=4 mm处)达到最大,为147.0 MPa。整体上看,试件接触表面上的各类应力最大区域处于与压头右侧接触边缘附近,该处存在较大的应力梯度。
2.2 微动裂纹萌生位置分析
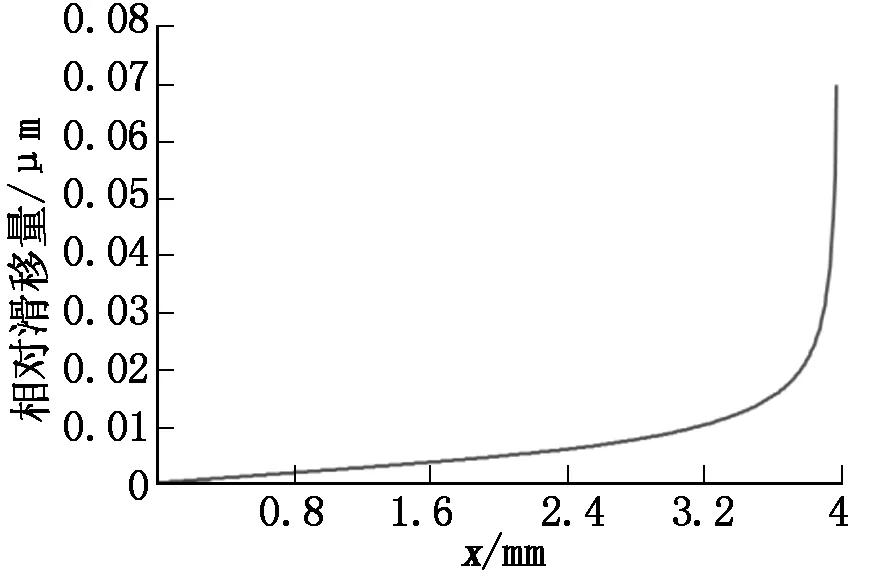
对考虑摩擦的接触问题,接触体受到法向和切向载荷共同作用,在切向载荷不足以使接触体发生整体滑动时,接触面产生微滑区和粘着区,随切向载荷的增加,微滑区逐步扩展到整个接触区域,从而产生宏观上的整体滑动[6]。库仑摩擦模型定义等效剪应力qx为接触面之间开始出现相对滑移时法向应力σn的分量,即qx=μσn,μ为摩擦系数,取0.5。当微动面上的剪应力τ≥μσn时,两接触面之间将相对滑移;当τ 图6 微动面τ/qx分布 采用目前广泛使用的微动综合参数R[10]来进一步验证裂纹可能的萌生位置[11],微动综合参数R最大的地方会首先萌生微动裂纹,R定义如下: R=μ×|σn|×|δ|×στ. (1) 其中:μ为摩擦因数;σn为法向应力;δ为相对切向位移;στ为切应力。该参数本质上是通过摩擦功反映磨损率(即磨损程度),磨损程度越大越有利于裂纹的萌生。 分别提取微动接触区域每个节点在最小轴向载荷和最大轴向载荷时的轴向位移和以及对应的压头位置节点的轴向位移和,即得到试件与压头在一个疲劳循环周期中的最小及最大轴向位移,则可算出试件与压头在一个疲劳循环周期中的轴向位移分别为: Uxs=Uxsmax-Uxsmin. (2) Uxp=Uxpmax-Uxpmin. (3) 则试件与压头的相对滑移幅度δ为: δ=Uxs-Uxp. (4) 试件微动面不同位置的相对滑移量如图7所示。由图7可见:对于面-面协调接触形式,试件微动面与压头的相对滑移量从中心位置(x=0 mm)到接触边缘(x=3.6 mm)基本呈线性缓慢增长;从x=3.6 mm到4 mm区间,相对滑移量迅速增加。根据式(1)计算出的微动综合参数R的分布如图8所示,R最大值在x=3.99 mm处,说明在该条件下裂纹萌生位置最可能出现在微动接触区边缘,与前述分析结果一致。 图7 微动面的相对滑移量 图8 微动综合参数R的分布 针对不同法向载荷、轴向载荷微动试验工况,从有限元分析结果中提取试件与压头微动接触面每个节点x方向的位移值,按式(2)、式(3)、式(4)计算出试件与压头的相对滑移量,得到微动滑移图如图9所示。图9表明:①滑移量几乎总是随轴向疲劳载荷的增加而增加,但在较低轴向载荷(<77.82 MPa)时,不管接触载荷有多大,滑移量均接近且较小,约为0.05 μm;②法向接触载荷越大,最大滑移量越小,法向载荷从62.5 MPa增加到125 MPa,最大滑移量从1.012 μm降到0.192 μm。 图9 不同法向压力σn、不同轴向载荷的微动滑移图 对于协调接触微动疲劳情形,微动表面并不一定必然存在微动滑移区,可能处于完全粘着状态,接触状态与轴向疲劳载荷、法向压力均有关系,滑移量几乎总是随轴向疲劳载荷的增加而增加,法向接触载荷越大,最大滑移量越小。如果存在微动滑移区,试件断裂位置处于粘滑过渡区;对于完全粘着微动状态,试件断裂的位置处于压头与试件的接触边缘。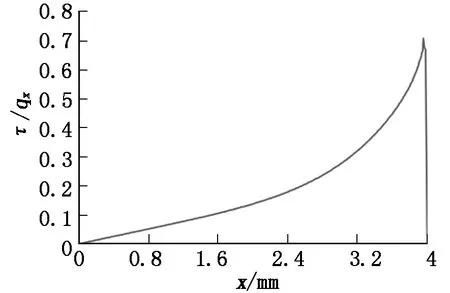

2.3 载荷对微动滑移量的影响

3 结论

