基于改进SIFT立体匹配算法的双目三维重建研究*

童 欣，殷晨波，杜雪雪，马 伟

(南京工业大学 机械与动力工程学院，江苏 南京 211800)

0 引言

基于双目的三维重建技术是立体视觉的一种重要实现方式，它基于仿生学原理，模拟人的双眼效应，利用两台位置固定而且参数相同的CCD摄像机获取同一景物的两幅图像[1]，使用立体匹配算法计算获得图像特征点对，并通过视差计算最终获取物体深度信息。双目立体视觉是被动获取被测物体深度信息的有效方法，由于其可以直接通过算法完成三维重建，且具有很强的适应性，因此近些年获得了广泛的关注。

立体匹配是双目立体视觉从平面图像中恢复立体信息过程中的关键技术。近年来，随着计算机技术的不断进步，双目立体匹配技术得到了长足发展。得益于双目立体匹配算法的速度与精度不断提高，以双目三维重建技术为主的立体视觉技术的应用场景进一步扩大，并已广泛应用于工业生产、自动化流水线、智能驾驶汽车、智能手机、移动支付和安全识别等领域[2]。尽管双目立体匹配的应用越来越广泛，但是仍然存在很多未解决的技术难题。这是由于双目立体匹配是一种过程性问题，在实验过程中其精度与速度变化的原因很难确定[3]。截至目前，还没有一种算法可以完美地对复杂立体匹配的整个流程进行处理，为此,本文提出一种改进SIFT立体匹配算法，主要针对双目匹配中图像视差计算和图像像素匹配效率低这一问题进行改进。

1 双目视觉

双目立体视觉算法是基于视差原理并利用成像设备从不同的位置获取被测物体的两幅图像，通过计算图像对应点间的位置偏差来获取物体三维几何信息的方法。

1.1 双目测距原理

双目摄像头能够测量物体到摄像头之间的距离，这是因为两个摄像头在拍摄物体时分别与物体存在一定的夹角，双目立体视觉算法可以根据夹角的数学关系推算物体与两摄像头之间的距离[4]。两台经过标定的摄像机在不同视角下同时获得被拍摄物体的图像或视频，用于恢复几何信息并重建其3D轮廓。双目测距的原理如图1所示。

图1 双目测距原理

图1中，Cl和Cr分别为左、右两个摄像头感光元件的中心，Pl和Pr分别为空间中任意的一点P在左、右相机成像平面上的投影点,Pl和Pr点所在的水平实线代表双目相机的成像平面，L为左、右两个摄像头感光元件中心的距离，f为感光元件到成像平面的距离，即焦距。假设分别以左、右两侧的摄像头光轴为Z轴，成像平面为X轴建立如图1所示的坐标系，则Pl和Pr的横坐标分别是Xl和Xr。从图1可以看出,△PPlPr∽△PClCr，根据三角形相似原理则有：

(1)

1.2 相机标定

本文采用以张定友标定法编写的OpenCV自带的相机标定算法对双目摄像机进行标定。该方法采用棋盘格作为标定模板，从3个以上不同的角度拍摄一组标定模板的图像即可对相机进行标定。在拍摄的过程中，只需要固定摄像机或模板任意一方，而不需要对摄像机或者被拍摄物体的运动参数进行求解。同时，张氏标定法假定摄像机的内部参数不变，只有外部参数发生变化。

使用OpenCV自带的Calibration文件在编译前需要设置一些基本参数：棋盘的高W,本文设置为6个黑白交界点；棋盘的长h,本文设置为8个黑白交界；棋盘格单个格子的长度s本文设置为2 mm。在进行具体标定操作时，标定板中棋盘格的长和高的个数需要确定，否则标定程序无法识别出相应的角点。

经过标定最终可以得到双目相机的内、外参数，分别包括单目标定后的内参矩阵、外参矩阵和畸变参数。经标定后的参数如表1所示。

表1 标定好的左、右相机参数

2 改进的立体匹配算法

双目立体匹配可以理解为寻找世界坐标系中同一个点在左、右两幅图片中像素点的坐标,这是由于双目立体匹配是一种过程性问题，在实验过程中其精度与速度变化的原因很难确定。截至目前，还没有一种算法可以完美地对复杂立体匹配的整个流程进行处理，本文提出一种主要针对双目匹配中图像视差计算和图像像素匹配效率低这一问题的改进算法。

2.1 经典的SIFT算法

在进行目标图片和源图片之间的特征匹配之前，检测出各自的特征并使用相应的特征描述子表示特征是非常重要的环节。检测算子是计算机视觉领域用于特征检测、描述和提取的综合算子,目前图像特征的检测算子有很多，不同的检测算子应用场景和性能也不相同，在实际运用中找到合适的检测算子是非常重要的。因此在研究三维重建的立体匹配算法时，采用了经典的SIFT算法进行图像的特征检测和匹配。

SURF、SIFT、ORB、FAST和Harris角点都是最常用的检测算法[5]。SURF算法相比于SIFT算法，其特征点的检测速度提升的很快，因此在大多数实时视频等流媒体的匹配上有着很广泛的应用。SIFT算法特征匹配的精度很高，所以其特征匹配的计算量也巨大，这使得双目匹配的过程花费时间相比SURF算法长很多，为此在一些需要实时处理的应用场景下SIFT应用较少。综上所述，SIFT算法检测的特征点更加精确，SURF算法检测的特征点速度更快，因此，在匹配精度要求较高且不考虑匹配速度的场合使用SIFT算法。经典的SIFT算法流程如图2所示。

图2 经典的SIFT算法流程

经典的SIFT算法中使用了高斯函数作为尺度空间表达的卷积算子，其计算公式如下：

(2)

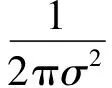
2.2 自适应模糊引入

由于经典的SIFT算子在特征检测时使用了二维高斯函数作为尺度空间表达的卷积算子，极大地降低了计算速度，严重影响了计算效率。高斯函数本身是一种指数函数，实际计算时对计算资源消耗较大，不能满足三维重建的实时性要求。为此结合SIFT立体匹配算法的步骤，将经典的SIFT算子中高斯模糊改成自适应模糊,其关键在于使用一种较小的平均加权模板与源图像进行迭代卷积[6]，每次迭代时自适应地改变各像素加权系数，以替代在SIFT匹配算法中的高斯模糊。设f(x,y)为输入图像，则一次迭代的计算步骤如下：

(1)梯度分量Gx(x,y)、Gy(x,y)的确定。梯度分量Gx(x,y)、Gy(x,y)由式(3)、式(4)计算:

(3)

(4)

(2)模板系数的确定。模板系数由公式(5)计算:

(5)

其中：k为参数，在计算之前需要设定，其大小对保留的突变边缘幅值进行了约束，本文k取值为10。

(3)对图像进行加权平均。使用公式(6)对图像进行加权平均：

(6)

其中：n为迭代次数，本文取为5。

3 实验结果与分析

通过使用不同的算法对左、右视角的图片进行特征点匹配处理，获得的图片如图3所示。由图3可以看出：处理的效果差别并不大，完成三维重建过程的经典SIFT算法的匹配率在89%左右，而改进之后的算法匹配率在91%左右，符合实验的要求。

图3 经典SIFT算法和本文算法处理图片的结果

经典SIFT算法和本文改进算法对不同分辨率图片进行特征匹配的运行时间对比如图4所示。

由图4可以看出：相比于经典的SIFT算法，本文的算法所花费的时间较少；随着分辨率的提高，两种算法所用时间不断增大，改进的算法所花费时间比经典SIFT算法也越来越少。由此可见，改进后的SIFT算法可以有效地降低双目立体匹配的运行时间。

图4 经典SIFT算法和本文改进算法花费时间对比

4 结语

本文针对在双目三维重建视觉匹配中图像视差计算和图像像素匹配效率低的问题，对已有立体匹配SIFT算法进行改进。实验表明：改进后的算法有效降低了双目立体匹配的运行时间，并为今后的双目三维重建工作提供了基础。