玻璃钢板的振动特性研究

陈 哲

(郑州机电工程研究所 第一研究室，河南 郑州 450015)

0 引言

纤维增强树脂基复合材料质量轻、耐腐蚀、可设计性强、比强度高，其在舰艇等工业领域正逐渐代替传统材料。英国的“威尔逊”号扫雷艇、“亚宾吉-21”号摩托艇都采用玻璃钢作为主体材料，俄罗斯AK-630型舰炮、美国MK42型舰炮均采用玻璃钢作为炮塔的材料，轻量化效果显著。与传统金属材料相比，纤维树脂基复合材料既能保证结构的承载能力，又能有效地提高结构的阻尼性能，对振动控制具有十分重要的意义。国内外学者针对玻璃钢的振动特性开展了一系列研究，徐宁等[1]采用实验方法研究了纤维用量和纤维排布方式对玻璃钢板的辐射效率和损耗因子的影响；武海鹏等[2]通过实验分别测试了纤维体积含量为60%的玻璃纤维和碳纤维复合材料的阻尼，发现单层纤维的角度对阻尼性能影响显著；史盼等[3]以约束阻尼复合结构为研究对象，采用动态黏弹谱仪和悬臂梁共振法研究了它的阻尼特性，发现采用玻璃钢作为约束层可以把复合结构的高阻尼性能拓展至宽频域和宽温域；贾宝惠等[4]通过理论推导与有限元仿真，探究了温度和湿度对正交各向异性复合材料层合板振动特性的影响；Lee S K等[5]采用试验方法研究了碳纤维铺层方向对碳纤维-环氧树脂基层合板振动性能的影响，研究发现可以通过改变纤维铺设角度来控制声压级；漆文凯等[6]采用多点激励、单点拾振的模态测试方法，分别对无损伤和有开孔损伤工况下的复合材料层合板进行自由振动和强迫振动测试，研究发现，开孔损伤的位置和大小对复合材料层合板的振动特性影响显著；Landge A D[7]采用有限元方法研究了具有不同类型材料配置和纤维角度的层合板的自由振动与强迫振动。然而，针对玻璃钢板的振动研究还不充分，尚不能满足工程应用的需要。

为了更加准确地预报玻璃钢复合材料层合板整体的振动特性，本文借鉴Matter等[8-9]提出的修正复合材料基本动态力学参数的方法，结合试验和仿真来确定单向玻璃纤维铺层的基本动态力学性能：首先对玻璃钢层合板进行模态试验，获得其各阶模态振型、固有频率和阻尼比；然后建立玻璃钢层合板的有限元模型，并代入材料参数初始值进行仿真分析，对比分析试验和数值仿真的结果，在保证试验和仿真得到的各阶模态振型一致的前提下，通过不断迭代优化有限元模型的相关参数，使有限元仿真结果不断趋近于模态测试获得的各阶固有频率，直至满足精度要求。

1 模态试验

试验模型为玻璃钢层合板，铺层采用单向玻璃纤维增强复合材料，单层表现为正交各向异性。玻璃钢层合板的几何参数为900 mm×900 mm×6 mm。对模型进行自由振动测试，获得模型的模态参数，为玻璃钢层合板模型参数的修正奠定基础。经反复迭代修正后的单向玻璃纤维铺层材料参数如表1所示，其中，E1、E2为材料在两个主方向上的弹性模量，G12、G13、G23为在三个平面内的剪切模量，υ12、υ13、υ23为在三个平面内的泊松比。

表1 单向玻璃纤维铺层材料参数

图1为模态试验装置。模型按照6×6等分，对每个节点进行编号，从左至右每一列编号依次为1～7、8～14、…、43～49。模态测试采用柔性绳悬挂法近似等效自由边界条件，加速度传感器的固定方式为石蜡粘合，模态辨识方法为多点激励、单点拾振，通过力锤敲击测试模型，敲击5次取平均得到其频响函数，根据频响函数辨识出各阶固有频率和模态振型。

图1 模态试验装置

2 试验结果

此处为了表达清晰和方便比较，只给出了结构前3阶弯曲模态。模态试验和有限元模拟得到的玻璃钢板前3阶弯曲模态对比分别如图2～图4所示。试验获得的玻璃钢板前3阶弯曲模态固有频率和阻尼损耗因子如表2所示。试验和仿真得到的玻璃钢板前3阶弯曲模态固有频率对比如表3所示。

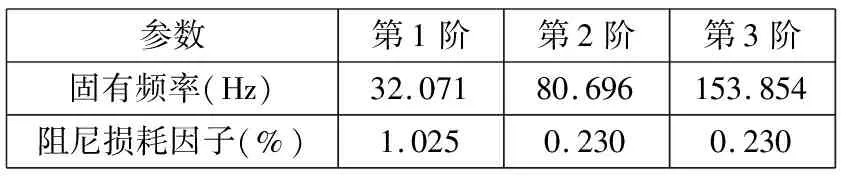
表2 试验得到的玻璃钢板前3阶固有频率和阻尼损耗因子

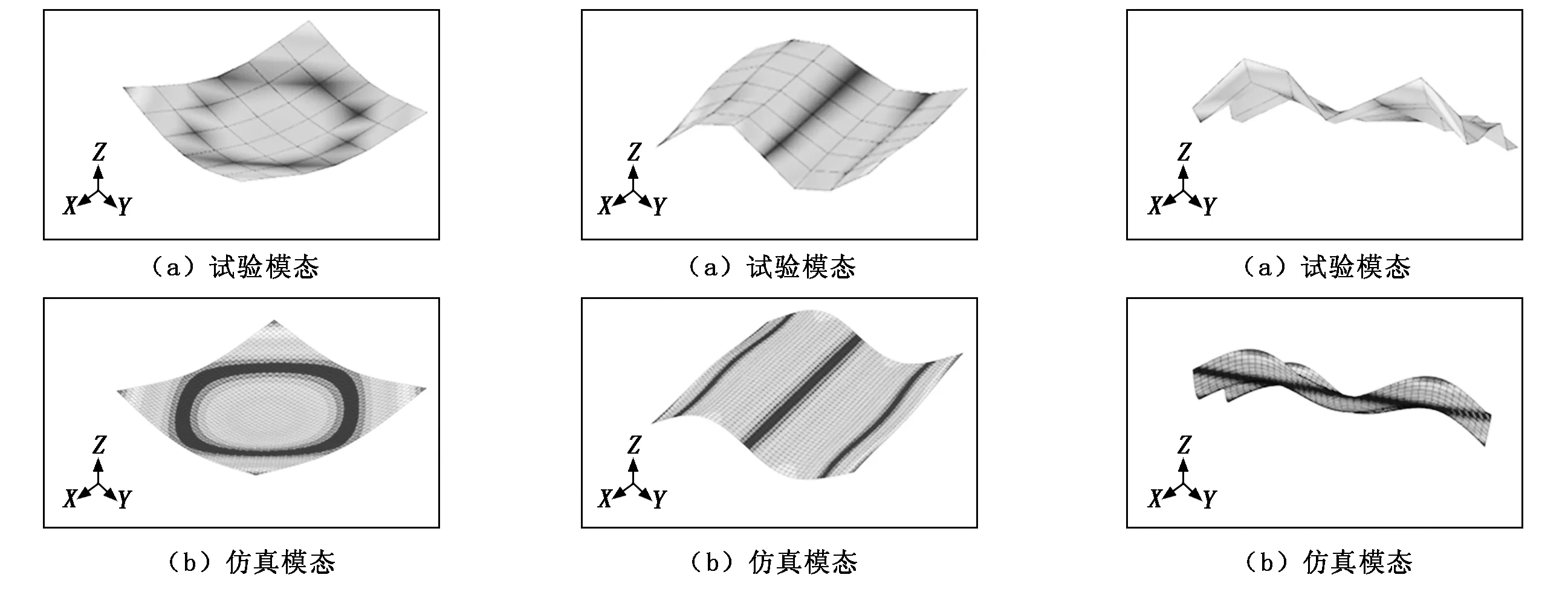
图2 玻璃钢板的1阶弯曲模态对比 图3 玻璃钢板的2阶弯曲模态对比 图4 玻璃钢板的3阶弯曲模态对比

从表3可以看出：采用迭代方法修正后的有限元模型进行仿真，得到的固有频率与试验结果的误差最大不超过3.9%，满足精度要求，说明建立的玻璃钢复合材料板的有限元模型可靠。经分析，误差产生的原因主要是有限元建模时忽视了真实模型的残余应力、界面缺陷以及局部纤维不规则排列(如图5所示)等因素。

表3 玻璃钢板前3阶固有频率试验和仿真结果对比

图5 玻璃纤维局部排列不规则

3 仿真分析

采用有限元软件ABAQUS建立玻璃钢层合板的数值计算模型。虽然模型在几何上是薄板，但是玻璃钢板的剪切模量相对较低，横向剪切变形不可忽略，所以为了在提高计算精度的同时降低计算量，本文模型采用模拟厚壳问题的Shell S4R单元。模型主要参数如下：正方形玻璃钢板边长L=0.9 m，厚度为6 mm；激励力作用在中心(x/2，y/2)处，幅值为1 N；测量频率f=1 000 Hz；边界条件为四边自由；空气中声速c=340 m/s，空气密度ρ空=1.225 kg/m3。

3.1 交替铺层角度改变对玻璃钢板振动性能的影响

对于纤维增强复合材料来说，在对纤维层的铺层角度设计时，为了避免纤维层合结构出现分层破坏，相邻铺层应尽量避免出现相同的铺层角度。此处选取±15°、±30°、±45°三种交替角度对玻璃钢板进行铺层，每层厚度为0.3 mm，总层数为20层，模态试验修正后的模型材料参数如表1所示。

图6为3种交替铺层角度下玻璃钢板的振动频响曲线。从图6中可以看出：在中低频段(0 Hz～800 Hz)，±15°和±45°两种铺层角度下的均方振速除峰值外大致重合，而且低于±30°角度下的情况；800 Hz～1 000 Hz频段内，±45°铺层角度的均方振速低于另外两种铺层角度。因此在进行铺层设计时，可以适当增大±45°铺层角的铺层比例。

图6 3种交替铺层角度下玻璃钢板的振动性能曲线 图7 多点激励对玻璃钢板振动性能的影响 图8 力的分布形式对玻璃钢板振动性能的影响

3.2 力激励的分布形式对玻璃钢板振动性能的影响

船舶的动力装置是船舶主要的噪声源之一，动力装置主要通过基座与船体相连，与基座的连接方式主要有点连接、线连接和面连接等。对于同样的振源设备，采用不同安装方式会导致不同的振动响应，工程中常需要选择使结构振动响应最小的安装方式。因此，本文分析了力激励的不同分布形式对玻璃钢板振动性能的影响。

3.2.1 多点激励对玻璃钢板振动性能的影响

力的激励个数及位置如下：

(1)单点：在(L/2,L/2)处施加幅值为1 N的简谐力。

(2)双点：在(L/3,L/2)和(2L/3,L/2)处各施加幅值为0.5 N的简谐力。

(3)四点：在(L/3,2L/3)、(L/3,L/3)、(2L/3,L/3)、(2L/3,2L/3)处各施加0.25 N的简谐力。

图7为激励点个数对玻璃钢板振动性能的影响。由图7可知：随着激励力个数的增加，玻璃钢板的均方振速明显降低。

3.2.2 点力激励、线力激励和面力激励对玻璃钢板振动性能的影响

分别选择单点激励、线力激励和面力激励进行比较，探究3种激励力对玻璃钢板振动的影响。力的分布形式及位置如下：

(1)单点激励：在(L/2,L/2)处施加幅值为1 N的简谐力。

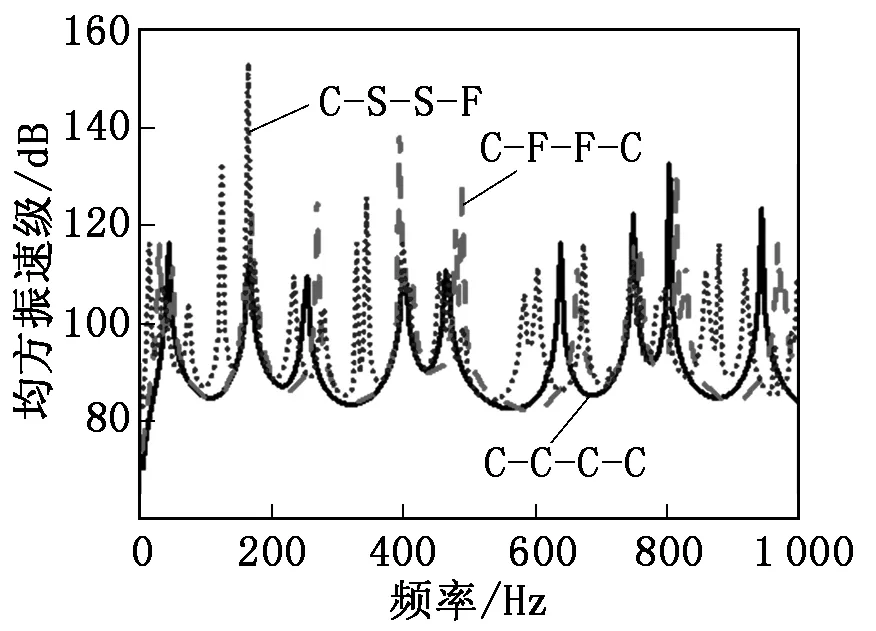
(2)线力激励：在(L/3

(3)面力激励：在(L/3

图8为力的分布形式对玻璃钢板振动性能的影响。由图8可知：在低频段，玻璃钢板的均方振速频响曲线在3种激励方式下非常接近;在中高频段，单点激励下的均方振速最大，面激励下的均方振速最低。由此可见，在工程应用中可以通过增大振源和玻璃钢板的接触面积来降低玻璃钢板的振动响应。

3.3 一般边界条件对玻璃钢板振动性能的影响

实际工程中，结构的边界条件通常比较复杂，不仅是典型边界条件如四边简支(S-S-S-S)、四边固支(C-C-C-C)、自由(F-F-F-F)等，还有可能是几种形式的组合,因此有必要探究非典型边界条件下玻璃钢层合板的振动特性。

图9为不同边界条件对玻璃钢板振动性能的影响。从图9可以看出：边界条件对玻璃钢层合板的振动特性影响显著，对比不同边界条件下的均方振速曲线发现，C-S-S-F边界条件下的共振峰最密集，C-F-F-C边界条件下的共振峰次之，C-C-C-C边界条件下的共振峰数量最少。由此可知：随着边界约束条件的增强，玻璃钢层合板振动曲线的共振峰数量减少，辐射能量也减小。因此，在工程实际中可通过增强层合板结构的边界约束条件来降低其振动水平。

图9 不同边界条件对玻璃钢板振动的影响

4 结论

本文以玻璃钢板为研究对象，基于模态试验对玻璃钢板的参数进行修正，采用有限元方法实现了复合材料层合板结构的振动特性预报。在验证玻璃钢复合材料板模型有效性的基础上，探究了纤维层铺设角度、力激励的不同分布形式和一般边界条件对玻璃钢板振动特性的影响规律。研究结果表明：

(1)对于交替铺层角度的玻璃钢板，±45°铺层角在0 Hz～1 000 Hz频段内具有更好的振动性能。

(2)增加激励力的个数或者将等大载荷分布在尽量大的面积上，可以明显降低玻璃钢板的振动水平。

(3)增强玻璃钢板的边界约束条件能够有效降低其振动水平。