带有体制转换特征的随机波动率模型下信用违约互换定价研究

陈文婷

(江南大学 商学院， 江苏 无锡 214122)

一、研究背景与理论意义

当今社会，金融危机时常发生，对经济和社会的发展造成了极大的危害。自20世纪30年代以来，最大的一次金融危机发生在2008年，这场危机给整个社会带来了前所未有的灾难，它不仅导致数以百计的大型金融机构相继倒闭或被政府接管，还导致了全球股市和房产市场出现严重下滑和低迷。在2015年政府工作报告中，李克强总理指出，我国需要“发展金融衍生品市场，创新金融监管，防范和化解金融风险”。对许多金融机构而言，其本质就是在经营风险，而信用风险是金融机构面临的主要风险之一，也是导致区域性乃至全球性金融危机的关键因素之一，它是贷款或投资债券中经常发生的一种风险，即借款者违约的风险[1]。近年来，随着互联网金融的蓬勃发展，有效地管理和控制信用风险成了我国乃至世界亟需解决的问题之一。

有效管理和控制信用风险的工具之一是信用衍生产品。它们具有分散信用风险、增强资产流动性、提高资本回报率、扩大金融市场规模与提高金融市场效率等五个方面的功效[2-3]。信用衍生产品在西方发展十分迅猛，而目前在我国尚处于初始阶段。自2016年以来，我国金融市场上违约事件频频发生。考虑到利用信用衍生产品有助于缓解银行业出现的“惜贷”、化解金融不良资产以及缓解中小企业融资难等问题，2016年9月23日，中国银行间市场交易商协会(NAFMII)发布了《银行间市场信用风险缓释工具试点业务规则》及配套业务指引文件，首次在中国推出了“中国版”信用衍生产品，该衍生产品在我国具有极大的应用前景，因此，对信用衍生产品定价展开研究具有强烈的时代意义，并且能够在很大程度上促进我国国民经济的良性发展。

在所有信用衍生产品中，信用违约互换(Credit Default Swap，简称CDS)是债券市场中最常见和最基本的信用衍生产品。针对某一特定的公司违约风险，信用违约互换合约为其提供了保险，其中，该公司被称为参考实体，该公司的违约被定义为信用事件。信用违约互换的买入方在信用事件发生时有权以债券面值的价格将公司债券卖给信用违约互换的卖出方，债券的面值被定义为信用违约互换的名义本金。信用违约互换的买入方有义务在合约期间向卖出方定期付款，直到该合约结束或者信用事件发生，定期付款行为发生在付款时间段的期末，但是合约的买入方也可以提前付款，或者每半年或每一年付款。当发生违约事件时，对合约进行交割的方式有支付现金或者交付债券实物，违约事件通常是指应当付款时未能支付、债务重组或者破产。从信用违约互换的运作流程来看，它的本质是信用违约互换合约的购买者将债券以面值递送给出售者，从而有效规避信用风险[4-5]。由于信用违约互换定义简单、容易实现标准化、交易简洁，自90年代以来，该金融产品在国外发达金融市场得到了迅速发展。

与普通的互换合约类似，对信用违约互换定价就是指确定其互换溢价。近年来，由于信用违约互换的迅猛发展，对其进行精确定价得到了业界和学术界的广泛关注。例如：Longstaff和Schwartz(1995)解决了在一个外生过程中信用差价期权的定价问题[6]，De Malherbe(2006)使用概率的方法确定了泊松过程下的信用违约互换的价格[7]。随着随机强度模型被用于违约事件，Brigo和Chourdakis(2009)在交易对手的违约和违约的信用违约互换参考信用之间存在关联的情况下考虑了该合约的交易对手风险[2]。

需要指出的是，能否给信用违约互换进行准确定价的必要条件之一是选取合适的信用风险模型。在现有文献中，信用风险模型主要分为两大类，各自代表着对违约过程形成的两种截然不同的看法：第一类模型，即简化模型，认为违约的产生是受短期冲击的影响造成的，具有突然性和不可预测性。这类模型主要由Artzner和Delbaen(1990)等学者提出[8]，并由Lando(1998)、Madan和Unal(1998)等学者通过修正得到进一步发展[9-10]。这类模型主要通过分析市场数据来提炼出公司的破产概率，在数学上比较容易处理，因而很受欢迎。然而这类模型比较严重的缺点是忽略了公司间破产的相关性。第二类模型也被称为结构化模型，是由默顿(Merton)(1974)在Black-Scholes期权定价模型的基础上发展而来的。[5]这类模型通常认为违约发生于公司价值低于某个阀值的情况，而公司价值的变化服从一个扩散过程，公司价值的突然下跌是不可能的，因此，违约的发生决不是意料之外的事件，而是在公司经营变化过程中逐渐产生的。

虽然默顿模型在信用衍生产品定价领域得到了广泛的应用，但是它的假设有诸多不合理[4][11]。譬如违约只是发生在债券到期日，这个假设与现实情况不相符。其次，它假设参照资产收益变化是一个布朗运动，其将来的分布为对数正态分布[5]，但这与实证研究的结果是相悖的。有学者指出，资产收益变化具有偏离布朗运动的特征，例如资产收益的变化具有长时间相关性，与标准对数正态分布相比，资产的分布往往具有更肥厚的尾等[12-13]。因此，许多学者试图修正默顿模型。一种思路是假设资产收益变化遵循非几何布朗运动，如假设参考资产价格服从一个泊松过程[7]、跳跃扩散过程[14]、广义分数阶布朗运动[4]等；另一种思路是假设参考资产价格由一个随机波动率模型控制，如Hull-White模型[15]、Stein-Stein模型[16]、海斯顿随机波动率模型[17]、单尺度随机波动率模型[18]、多尺度随机波动率模型[19]等。需要指出的是，在所有随机波动率模型中，海斯顿随机波动率模型受到了最为广泛的关注，该模型不仅满足了市场的一些基本特征，如能够体现波动率的非负性和它围绕着一个长期均值水平来回波动等，海斯顿还找出了该模型下欧式期权的一个半封闭形式的解析解，使得该模型可以快速而精准地进行校正，从而可以很好地运用到实际金融市场中去。

尽管上述模型都在一定程度上修正了经典的默顿模型，但是它们中的绝大部分仍然无法捕捉到真实市场状态不断变化的事实，因此，体制转换模型也就应运而生了。体制转换模型可以合理解释经济状况、宏观经济环境的变化，体制转换模型反映了金融市场中的利率、汇率、股票回报等均与经济状态有关，它假定在给定市场经济状态时，风险资产价格演变过程由某个特定的模型来刻画；当市场经济状态发生变化时，价格演变过程切换到另外的模型中去。我们可以认为体制转换模型符合一般的经济周期理论。体制转换模型最早由Hamilton(1990)提出并运用到金融计量领域[20]，大量的实证研究也证实了金融市场中确实存在体制转换的特征[21-23]。Bollen等(2000)学者利用体制转换模型来刻画汇率的波动情况[21]。So等(1998)学者将体制转换引入到随机波动率模型中，得到了一个带有体制转换特征的随机波动率模型[22]。Vo(2009)指出，So等(1998)学者提出的模型不仅能够加强随机波动率模型对资产价格的预测能力，同时也能够反映金融市场中重大事件的发生对资产价格的影响。[23]由于海斯顿随机波动率模型在数学上具有很强的处理性，带有体制转换特征的海斯顿随机波动率模型引起了学术界和业界的共同关注。例如：Elliott和Lian(2013)在海斯顿模型的长期回归均值水平中引入体制转换机制，并考虑了在该模型下波动率互换产品的定价。[24]He和Zhu(2018)假设了波动率的波动率可以在不同状态下进行切换，并利用渐近展开法得出了相应的欧式期权价格的一个近似解[25]。最近，He和Chen(2020)将体制转换特征引入到随机波动率利率模型中，提出了一个带有体制转换特征的混合随机波动率利率模型。(1)He X J, Chen W T. A semi-analytical formula for European options under a hybrid Heston-CIR model with regime switching[J]. International Journal of Finance and Economics, 2020, doi: 10.1002/ijfe.1792.通过严格的数学推导，他们找出了该模型下欧式看涨期权的解析表达式，并通过实证研究，证明了该模型在模拟资产走势方面的优越性。

为了使模型能够更好地模拟公司资产(参考资产)的价格走势，本文以Elliott和Lian(2013)提出的带体制转换特征的海斯顿随机波动率模型为蓝本[24]。在该模型下，假设波动率的长期均值水平可以在不同的状态中进行切换，由于该模型参数众多，在此模型下无论是从解析角度还是数值角度考虑金融衍生产品的定价都并非易事。尽管如此，本文依然推导出了在该模型下信用违约互换价格封闭形式的解析表达式。文中还通过数值模拟实验定量研究了各种参数变化，特别是引入体制转换特征对信用违约互换价格的影响。值得一提的是，本文所提出的方法具有一定的普适性，在一定程度上可以推广到求解带体制转换特征的模型下其他金融衍生产品的价格。

二、信用违约互换价格的解析表达式

本文从解析解的角度重点研究带体制转换特征的海斯顿随机波动率模型下信用违约互换的定价问题。首先，简单介绍默顿模型和带有体制转换特征的海斯顿随机波动率模型；其次，推导出在带有体制转换特征的海斯顿随机波动率模型下参考资产的破产概率；最后，通过分析现金流进一步确定新模型下信用违约互换的价格。

1. 定价模型

如前文所述，对信用违约互换合约进行合理定价的关键在于选取合适的定价模型。我们将首先回顾经典的默顿模型，在此基础上，引入带有体制转换特征的海斯顿随机波动率模型。

默顿模型是结构化模型的重要代表[5]。这里的“结构”指的是公司的资本结构，即为债券和股权之间的资本关系。结构化模型的基础思想是通过分析企业的财务资本结构情况进而判断企业违约风险的可能性，简而言之就是通过比较企业资产市场价值和其债务市场价值之间的关系来做出违约风险的判断。默顿模型的基本思想是把负债经营的企业视为债权人所持有的证券，同时也将其看作是一个被股东所持有的以该证券为标的物的看涨期权，当企业总资产的市场价值高于债务的市场价值时，股东行使看涨期权，偿还公司债务，进而继续拥有公司；可是如果当债务市场价值高于企业总资产的市场价值时，则公司发生破产，公司将被公司所有人出售给债权人，由债权人拥有公司。期权的价值和企业违约的可能性之间存在着重要的联系，并且企业资产价值与企业负债面值之间的差额的期望与公司波动率的比值也是影响期权价值的重要因素。违约率是债务到期时企业资产的市场价值小于或者等于企业负债的账面价值的概率。在默顿模型中，市场被假定是完全的，也就是说，不存在任何的交易成本，同时，公司资产被假定为不存在流动性的调整，公司资产的价值被假设为服从几何布朗运动。然而，正如前文指出，该假设具有诸多不合理性，比较突出的是这种假设不仅忽略了公司资产价格的波动率不是常数这一事实，也无法将重大事件的发生对公司的影响考虑在内。

针对以上两点，本文选用带有体制转换特征的海斯顿随机波动率模型来模拟公司资产价格的走势。在这个模型下，参考资产的波动率被假设为服从一个均值回归过程，且其长期均值水平可在不同的状态下进行切换。具体来说，假设参考资产的价值St在风险中性测度Q下满足带体制转换特征的随机波动率模型，即令t为当前时间，vt、r分别为参考资产价格变化的波动率和无风险利率，St满足：

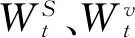
且在这两个状态下的转移率服从一个泊松过程，即

P(tij>t)=e-λijt(i，j=1，2，i≠j)

其中(·)T是向量的转置，tij是随机变量Xt在状态i中的逗留时间，λij为随机变量Xt从状态i转至状态j的转移率。此外，在这种情形下，波动率的长期均值可以分别表述为

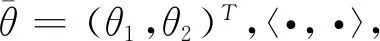
dYt=μ(Yt)dt+Σ(Yt)dWt，

(1)

其中

zt=lnSt，W1，t与W2，t是两个线性无关的几何布朗运动，μ(Yt)是漂移率，其定义为

其中，

∑(Yt)是波动率矩阵，它可以表述为

进一步可表述为

其中，H是个2×2×2的矩阵，其元素Hij(1≤i，j≤2)是2×1的向量，具体为

由于漂移项也可以表述为一个仿射函数，因此，上述随机过程(1)具有仿射相关性，该性质也是求解公司破产概率的重要性质之一。本文接下来将重点阐述如何在该模型下求解公司的破产概率。

2.公司破产概率

公司的破产概率是信用违约互换合约中最重要的因素之一，它代表公司在一定时期内发生违约的可能性，这也是信用违约互换合同价格推导的关键一步。本文将考虑如何定量地确定这个重要因素。

令D为信用违约互换的破产障碍，即参考资产价格一旦下跌至D，则公司违约发生。根据金融意义，可知公司发生破产的概率为PQ(ST≤D)，其中PQ是在测度Q下的概率。进一步令zT=lnST，那么就有PQ(ST≤D)=PQ(zT≤lnD)。

再根据期望与矩母函数的关系，可得

其中j是虚数单位，a=(0，0)T，b=(-1,0)T，Im(·)是取虚数部分运算，f(φ,Yt,Xt,t,T)是广义矩母函数，具有如下定义f(φ,Yt,Xt,t,T)=E[eφ·YT|Yt,Xt]，其中φ=(φ1,φ2)T。从上述过程可以看出，如果这个矩母函数可以顺利求出的话，那么破产概率也可以很容易的求得。

值得指出的是，由于马尔科夫链Xt的存在，直接计算广义矩母函数f很困难。为了简化求解过程，本文重新将广义矩母函数表述为

f(φ,Yt,Xt,t,T)=E{E[eφ·YT|Yt,XT]|Xt}=E[m(φ,Yt,t,T|XT)|Xt]，

其中m(φ,Yt,t,T|XT)是广义条件矩母函数。从f与m的关系可以看出，一旦确定了m，f就可以通过再求一次期望获得。因此，求解破产概率在现阶段的首要任务变为确定m。下面的定理阐述了该条件矩母函数的确定方法。

定理1. 如果标的资产价格和其波动率遵循随机微分方程(1)，则其广义条件矩母函数可以表述为m=eC(φ;τ)+D(φ;τ)·Yt，其中·代表向量的点积，τ=T-t，

证明：根据Duffie等(2000)中提出的仿射跳跃扩散过程的性质[26]，可知广义条件矩母函数可以表述为m=eC(φ;τ)+D(φ;τ)·Yt，其中函数C(φ;τ)、D(φ;τ)满足如下的耦合常微分方程组：

根据D(φ;τ)的定义，可得

很显然，D1(φ;τ)是一个关于τ的常数。为了求解D2(φ;τ)，采用平移变换D2(φ;τ)=D2(φ;τ)-φ2，可得如下齐次初始条件的Riccati方程：

其解为

有了D(φ;τ)的表达式，C(φ;τ)只需在其满足的常微分方程两端对τ做积分。这就完成了整个定理1的证明。

上文中既然已计算出广义条件矩母函数m(φ,Y,t,T|XT)的具体表达式，那么只需将最外层的期望计算出来即可确定广义矩母函数f，即

f(φ,Yt,Xt,t,T)=E[m(φ,Yt,t,T|XT)|Xt],=eD(φ;τ)·YtE[eC(φ;τ)|Xt]。

根据Elliott和Lian(2013)中的结论[24]，E[eC(φ;τ)|Xt]可以通过以下方式显式地计算出来，即

其中，I=(1，1)T，<·>代表向量内积，A是马尔科夫链Xt的转移概率矩阵，定义为

而对角矩阵B可以表述为

其中diag[·]代表该矩阵是对角矩阵，且其对角线上的元素是由该函数作用的向量的每个元素组成。因此，广义矩母函数f(φ,Yt,Xt,t,T)最终可以写为

f(φ,Yt,Xt,t,T)=eD(φ;τ)·Yt，

其中

至此，我们已经推导出了公司破产概率PQ(ZT≤lnD)的解析表达式，即

(2)

这可以认为是进一步确定信用违约互换合约价格的关键一步。本研究将通过分析现金流来进一步确定该合约的价格。

3.信用违约互换合约的价格

本研究将根据上述得到的破产概率进一步分析相应信用违约互换价格的解析表达式。需要指出的是，和一般的金融衍生品不同，信用违约互换的价格是指合约买方需要定期支付给卖方的金额，通常用参考资产名义价值的百分比来表示。

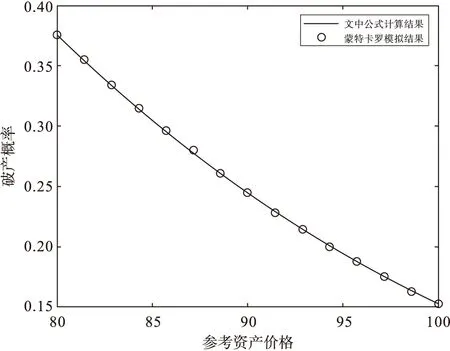
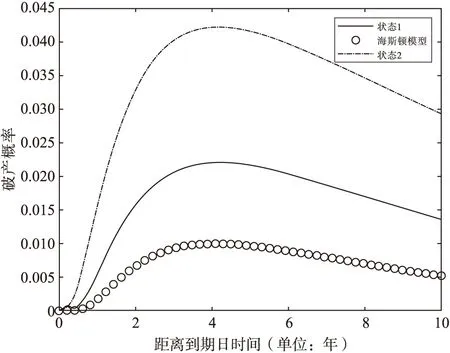
为了确定该信用合约的价格，首先需要分析买卖双方的现金流状况。假设c为信用违约互换的价格，M为该合约的面值，并假设在离散时间点ti(i=0，1，2，…，N且0=t0

其中r是无风险利率。另一方面，对于卖方来说，当且仅当公司在T时刻发生破产时，需要支付给买方(1-L)M现金，因此，卖方的现金流为P2=e-rTM(1-L)PQ(ST≤D)，对于互换合约来说，由于其建立在对买卖双方都公平的基础上，因此，它的初始价值为0，因此，有P1=P2，即

根据上一小节中的结论，可以推导出c的最终表达式为

从上述价格的解析表达式可以看出，该表达式只包含一个一重积分，因此，它可以很容易在计算机上实现。进一步的，有了该解析表达式，信用违约互换的各种风险参数，如Δ、Γ等的解析表达式都可以通过对价格表达式c做相应参数的微分得到。此外，由于解析表达式的易实现和可以达到任意精度的特点，使用该解析表达式可显著提高模型校正效率。因此，本研究中的理论工作大大增强了模型的实用性和可推广性。此外，上述信用违约互换价格的解析表达式也有助于定量分析相关参数变化对价格的影响。

三、数值模拟与讨论

上文从数学角度严格推导出了信用违约互换合约价格的解析表达式。因此，在理论上没有必要再进行数值模拟来讨论该价格的精度。然而，为了使读者更信服我们的结论，本文将公式(2)计算出的结果与其他方法计算出的结果进行比较，此外，本文还将定量分析不同参数的变化，特别是在引入体制转换特征后对信用违约互换价格的影响。

在下面的算例中，除非进行特殊说明，统一采用如下的参数设置。在带体制转换特征的海斯顿随机波动率模型下，假设当前的状态为状态1，无风险利率r=0.03，破产障碍D=80，当前参考资产价格S0=90，当前波动率水平为v0=0.05，相关系数ρ=-0.8，均值回归速度κ=10，波动率的波动率σ=0.1，转移率λ12=λ21=10，距离合约到期T-τ=5，并规定在合约生存期内完成20次支付。状态1对应的θ1=0.05，状态2对应的θ2=0.1。对于将要进行对比的海斯顿随机波动率模型，参数设置如下：r=0.03，D=80，S0=90，v0=0.05，ρ=-0.8，κ=10，σ=0.1，T-τ=5，θ=0.05。

首先将检验新推导出的信用违约互换价格的正确性。由于破产概率是信用违约互换价格中最重要的一部分，为了方便起见，该实验将针对计算破产概率进行。我们将从公式(2)中计算出的破产概率与由蒙特卡罗方法直接计算出的破产概率进行比较，由于蒙特卡洛的计算结果将作为一个精确解来做为对比参照物，因此需要大量的样本路径来模拟资产价格走势。在本实验中，我们采用了100，000条路径来完成蒙特卡罗模拟。两种方法下的计算结果如图1所示。从图1-a中可见二者吻合的非常好，从图1-b可观察到二者间的点对点相对误差不超过1%。这些都有力地支撑了我们新推导出的公式的准确性，表明了该公式可以很安全地运用到实际金融市场中去。另一方面，从图1-a也可以看出，当参考资产的价格变大时，公司破产概率也逐渐变小。这是非常合理的，在不考虑价格有较大的跳跃变化的前提下，如果参考资产价格越大，那么在短时间内公司资产越不容易触及破产障碍，公司就越不容易破产。

图1-a 计算结果与蒙特卡罗算法比较

图1-b 点对点相对误差

有了该公式的正确性检验，下面我们将定量研究不同参数变化对破产概率的影响。首先研究的是引入体制转换机制的影响。在图2中展示了在带体制转换特征的海斯顿随机波动率模型与海斯顿随机波动率模型下，破产概率对距离到期日的变化。从这张图中可以观察到一个有趣的现象，即在这两个模型下，破产概率都是先单调递增，达到某个水平后，然后再递减趋于平缓。进一步仔细观察可以发现，即便将海斯顿随机波动率模型下的波动率长期均值水平设置成与带有体制转换特征的海斯顿随机波动率模型下状态1中相同的长期均值水平，前者的破产概率也要低于后者的破产概率。从金融角度分析，这是十分合理的。由于可在不同的状态中进行切换，从平均意义的角度来说，带有体制转换特征的海斯顿随机波动率模型的长期均值水平会处于状态1与状态2之间，将略高于相应的海斯顿随机波动率模型下的长期均值水平，导致带有体制转换特征的模型波动率水平总体高于相应的不带体制转换特征的波动率水平，因此，前者的破产概率高于后者。

图2 两种模型下破产概率的比较

在新的模型中，体制转换的频率主要由转移率来决定。因此，为了进一步定量研究引入体制转换的影响，下面一个数值实验将从转移率变化引起信用违约互换价格变化的角度展开。在新的模型下，为了简化起见，不妨假设两个转移率相等，即λ12=λ21=10*z，其中z为缩放参数。图3展示了在本文所采取的模型和海斯顿随机波动率模型下，信用违约互换价格关于z的函数图像。从图中可以清楚地看出，无论转移率如何变化，海斯顿随机波动率模型下信用违约互换的价格不随着转移率的改变而改变，这是非常合理的，因为海斯顿随机波动率模型本身就与转移率无关。而在带有体制转换特征的海斯顿随机波动率模型下，当转移率都为0时，该模型就不具备体制转换特征，因此，此时该模型下信用违约互换的价格与海斯顿随机波动率模型下的价格一致。由图3还可以看出，当状态1中的长期均值水平小于状态2中的长期均值水平(θ1(=0.05)<θ2(=0.2))时，新模型下信用违约互换的价格是一个关于转移率的单调递增函数；反之，如果当状态1中的长期均值水平大于状态2中的长期均值水平(θ1(=0.05)>θ2(=0.01))时，新模型下信用违约互换的价格是一个关于转移率的单调递减函数。此现象的发生与模型的金融本质是密不可分的。从金融角度分析，转移率的增加，意味着从状态1转移到状态2的概率增加，当状态1中的长期均值水平小于状态2中的长期均值水平时，转移到状态2中频率的增加会引起参考资产平均波动率的增加，进一步引起公司破产概率的增加。由于信用违约互换价格与破产概率是正相关的，因此，在状态1中的长期均值水平小于状态2中的长期均值水平的前提下，从状态1转移到状态2的频率增加将最终导致信用违约互换的增值，反之亦然。

图3 信用违约互换价格关于缩放因子的函数图

图4展示了信用违约互换价格与距离到期日时间的关系。从该图中可以清楚地发现，与破产概率类似，信用违约互换价格与距离到期日时间是一个先单调递增后单调递减的函数。这个现象也可以从信用违约互换价格与破产概率是正相关的角度来解释。

图4 信用违约互换价格关于时间的函数图

最后我们研究的是信用违约互换价格与支付次数的关系。如图5所示，当支付次数增加时，信用违约互换价格降低，反之亦然。从金融的角度来考虑，这是非常合理的，因为在补偿金保持不变的情况下，信用违约互换买方支付的次数越多，每次支付的金额就越少。

图5 信用违约互换价格关于支付次数的函数图

四、结论与研究展望

本文主要研究了在带有体制转换特征的海斯顿随机波动率模型下信用违约互换的定价问题。通过分析现金流和公司的破产概率，本文得到了在新模型下信用违约互换价格的一个解析表达式，并将其与蒙特卡罗方法计算出的结果进行比较，证实了该价格表达式的正确性。基于该价格表达式，本文还进行了数值模拟实验，特别是引入了体制转换特征，从定量的角度充分分析了不同参数变化对信用违约互换价格造成的影响。

需要指出的是，在本文中虽然新的模型和原来经典的默顿模型相比更加精确，同时也更加符合实际的情况，但是新模型依然有许多的不足之处。例如：将波动率的长期均值水平假设为可在不同状态中进行切换的合理性有待利用实际市场数据进一步验证；其次，在新模型中，利率被假设为常数，且没有考虑公司资产的回报率等，显然，这与现实之中的情况有很大的出入。另一方面，在本文考虑的信用违约互换合约中，公司只有在信用违约互换合约到期时才有可能会发生破产，这显然是不合理的，现实的经济活动中公司破产会发生在任意时刻，而并不是只能在到期日时发生。在这些与实际并不完全吻合的假设下建立模型，依据该模型计算出的结果往往与现实情况还存在着误差，因此，修正后的新模型还是不能够精准地描述市场状态。

为了使定价结果更加精确，我们应该对模型的假设前提进行不断优化和修正，不断对模型进行调整改进，使它更加符合实际的市场情况，同时也让模型在实际市场的运用之中发挥着更大的作用，这将是今后的一个重要研究方向。