基于观测器的楼宇恒压供水控制系统故障诊断

刘迎松，杨 帆，赵莹莹

（天津城建大学 控制与机械工程学院，天津300384）

随着人民生活水平的不断改善，对高层楼宇供水质量的要求也越来越高，不仅要安全稳定，而且要节能环保[1-2]. 高层楼宇恒压供水控制系统具有非线性、纯滞后、大惯性等特性，在使用时难免会发生故障，影响住户正常用水[3-5].然而在目前的故障诊断方法研究中，对于恒压供水控制系统故障诊断的研究相对较少.

在现有的故障诊断方法中，对于控制系统中执行器或者传感器产生的故障，往往采用观测器即故障检测滤波器，通过产生残差来实现故障诊断.但是在故障检测中难免存在一些不确定的干扰信号，使检测出来的信号与原信号之间存在一定误差，造成观测器对故障信号不敏感.关于系统的故障诊断方法，大量学者进行了研究.文献[6]基于子空间识别和Kalman 滤波技术对风力涡轮机传感器故障检测与隔离进行了研究；文献[7-9]更多采用了滑模控制技术进行系统的故障检测.如基于解析模型的检测方法、运用滑模控制技术，实现了PWSM 驱动系统的故障检测[7]；通过分解原系统实现故障与干扰的分离的检测方法[8]；基于初始故障检测的双旋翼直升机自适应滑模观测器综合设计，实现了对系统微小故障的检测与诊断[9].文献[10]考虑的是非线性系统传感器故障检测与隔离，利用滑模控制得以实现.

本文主要解决楼宇恒压供水控制系统中的执行器故障.考虑到实际应用为广义非线性系统并且存在未知干扰，首先通过设计全维观测器证明了系统状态误差为全局渐近稳定；然后通过设计H∞观测器实现系统的鲁棒故障诊断；并且引入了解耦合的方法来解决干扰解耦问题，通过产生残差信号，对系统的故障进行诊断，对未知干扰更加具有鲁棒性，具有一定的实际意义.

1 恒压供水控制系统分析

1.1 供水过程分析

恒压供水控制系统是楼宇自动控制系统中的重要部分.恒压供水系统主要由变频器、PLC、压力变送器和终端水泵机组组成[11]，供水系统的工艺流程如图1 所示.

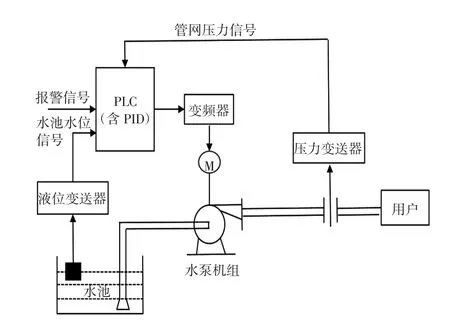
图1 恒压供水系统工艺

本恒压供水系统构成了一个完整的闭环控制系统：当管网压力不足时，通过压力变送器传递信号给控制器，即PLC；然后传递信号给变频器，通过变频器控制水泵机组在合适的速度转动，使得管道供水流量一直处于一个恒定状态[12].恒压供水控制系统方框图如图2 所示.

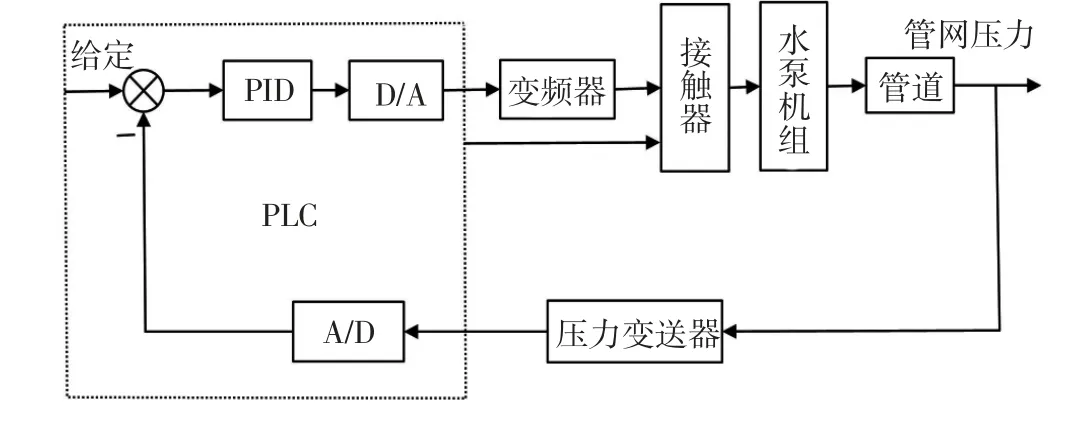
图2 恒压供水控制系统方框

1.2 恒压供水系统建模

恒压供水控制系统的数学模

式中：x∈Rn为恒压供水系统的状态向量；u∈Rk为系统的控制输入向量；η∈Rq为未知输入；y∈Rp为管网压力信号；φ 为恒压供水系统中的非线性部分；f（t）∈Rm为恒压供水系统中的故障向量；A、B、C、D、F 为适当维数的矩阵；E 为奇异常数矩阵.

系统中的非线性部分满足Lipschitz 条件，即‖φ（x，u，t）-φ（x^，u，t）‖≤γ‖x-x^‖，其中Lipschitz 常数为γ.

2 观测器设计与稳定性分析

2.1 全维观测器设计

为了判断楼宇恒压供水系统的状态误差是全局渐近稳定的，设计如下形式的全维观测器为

其中：L 为待定观测器参数；x^（t）为对x（t）的估计向量.首先定义e=x-x^为观测器状态估计误差向量.那么由式（1）和（2）可以得到的方程为

本文应用李雅普诺夫稳定性理论以及线性矩阵不等式的处理方法，为了确保状态估计误差的渐近收敛性，以下定理给出确保状态误差近收敛于零的充分条件.

假设1 N∈Rp×n与非奇异矩阵N∈Rn×n为线性矩阵不等式的解，具有增益L=M-TNT的式（2）为系统式（1）的全维观测器，误差状态e（t）全局渐近稳定.

定理1在系统式（1）中，存在形如式（3）的全维观测器的充分必要条件是使下列线性矩阵不等式有解，其中存在M 和N 两个矩阵.

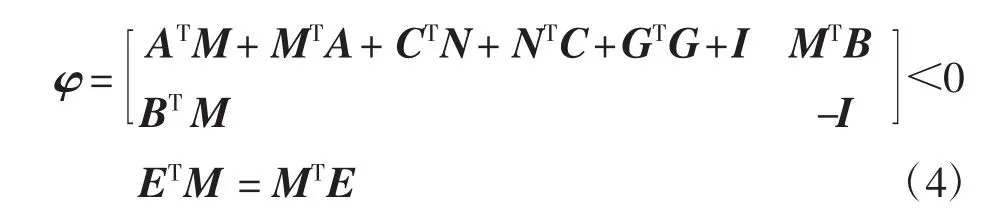
证明方法类似于文献[13]，就是把设计观测器的问题转化成了求解线性矩阵不等式的问题[13].

要想将不等式（4）转化为严格的线性矩阵不等式.设E⊥∈R(n-s)×n满足E⊥E=0，且rank（E⊥）∈n-s，则有以下引理.

引理1[13]从定理1 的条件中可得知存在正定矩阵X∈Rn×n，矩阵Y∈R(n-s)×n和Z∈R(r×n)使得以下矩阵不等式可解.

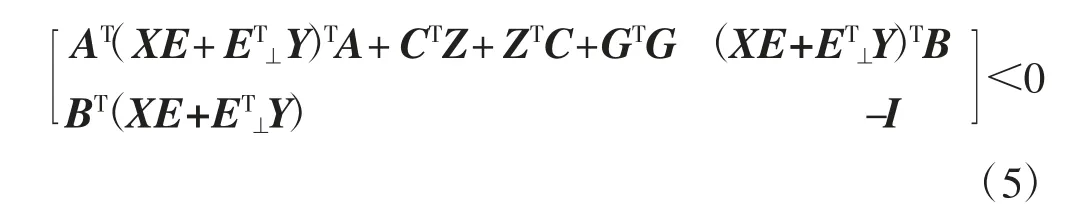
证明类似于文献[13]，由以上引理1 和定理1 可得，若存在正定矩阵X∈Rn×n和矩阵Y∈R(n-s)×n，则系统可进行全维观测器的设计，存在Z∈R(r×n)使得线性矩阵不等式（5）成立.

2.2 状态误差稳定性分析

为了对楼宇恒压供水系统中的管网压力和水池水位状态信号的稳定性进行分析，采用了基于李雅普诺夫稳定性理论的分析方法.

若AC=A+LC，选取V=eTETMe 李亚普诺夫函数，设λ0=λmin（-Ω）及φ=φ（x，u，t）-φ（x^，u，t），那么λ0＞0 且‖φ‖≤‖Ge‖.

于是V 与误差系统（3）的导数为

引入记号λm= λmax（ETM），则λm＞0 且V =eTETMe≤λm‖e ‖2，即那么V˙≤-λ0这就可以得到其中

根据Schur 补引理[14]，可得式（4）中的不等式为

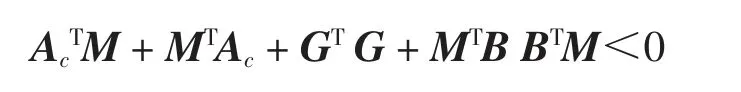
等价于不等式为

根据上文中的分解式可得

所以存在充分小标量ε0＞0，使得（1+δ0）GTGQ2＜

不失一般性，仅考虑n-s≤p，其他情况类似.利用P2B 矩阵的奇异值分解可得其中：W1∈R(n-s)×(n-s)；W2∈Rp×p为正交矩阵；Δ∈R(n-s)×(n-s)为对角矩阵，对角位置上的元素都是降维排列的正数.那么

注意到e = Q1e1+ Q2e2以及e1= P2Bφ，那么由得

进一步，根据上文推导可得

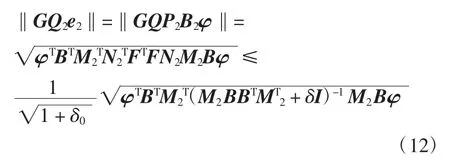
3 H∞观测器的设计与故障诊断

3.1 H∞观测器的设计

为了实现对楼宇恒压供水控制系统的故障检测，本节是要设计如下式的观测器对系统向量x（t）进行估计，即

其中：z（t）为观测器的状态；H，K，O，R 为适当维数的矩阵.

定义观测器误差向量为

接下来由观测器误差推导可得e˙= z˙-KEx^.

由假设联合式（14）的推导取O=O1+O2，O1=HR，可得

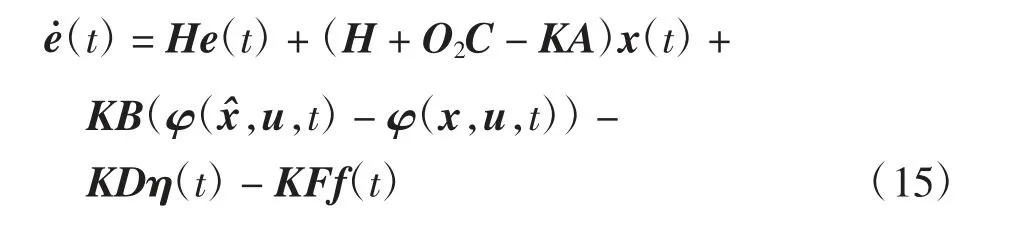
定理2根据观测器的动态方程，若满足下列假设，观测器误差指数收敛于0，即指数x^（t）收敛于x（t）.

假设3 H+O2C-KA=0，KD=0，KF=0.

证明类似于文献[15]，如果上述假设3 中KD≠0，那么误差方程为

由式（14）的推导可以得出O2是唯一要计算的量，那么取李雅普诺夫函数为V（t）=e（t）TPe（t），P 正定对称实矩阵，计算关于t 的导数可得在假设2 下，如果存在适当维数矩阵W＞0，O2以及实常数θ＞0，通过Schur 补引理可得LMI 为

有解，可以求得O2和K，从定理3 的假设3 可以求得H.H∞观测器设计完成.

3.2 鲁棒故障诊断

为了实现恒压供水系统的故障检测，残差信号必须对未知的干扰不敏感，而且还要做到对系统中的故障敏感.供水系统的残差产生于控制系统的干扰和故障，根据文献[16]得恒压供水系统的残差信号为

式中：re（t）∈R 是供水系统的实际故障与故障观测器对比产生的残差信号，U1∈R；U2∈R；e（t）∈Rd是系统的状态误差向量，re（t）即故障的显示器.为了避免不必要的干扰，这就需要故障诊断方案满足定理3 的条件2 中的KD=0，同时为了残差信号能对故障作出反应要满足条件KF≠0.

这样残差信号可以描述为

未知干扰被完全解耦，残差信号独立出来即

由上文中式（18）可以求出K，代入式（21）可以求出U1和U2.那么根据式（19）就可以求出残差信号，然后通过设定阈值，就可以实现对恒压供水系统的故障诊断.

4 仿真实验分析

为了验证对楼宇恒压供水控制系统故障诊断的有效性，以某高层住宅楼恒压供水系统为例，并联多台水泵共同运行；采用三相四线保证系统稳定供电，PLC 选择S7-300、压力变送器输出4～20 mA 的标准电流信号，控制变频器的频率在0～50 Hz.通过实际测试收集一组参数，并且使用上文中设计的故障观测器，利用MATLAB 进行仿真实验.其参数矩阵为

解不等式（4）可得

对楼宇恒压供水控制系统中的压力电流信号状态量x1和水位电流信号状态量x2，它们的状态误差稳定性分析的仿真结果如图3-6 所示.

图3 状态量x1 与状态量x1 的估计

图4 状态量x1 与其估计量x^1 的误差e1

图5 状态量x2 与状态量x2 的估计

图6 状态量x2 与其估计量x^2 的误差e2

通过对仿真结果的分析，从图3 和图4 中看出，系统的状态量x1与其估计量x^1的误差e1逐渐收敛为0，那么可以得到误差e1全局渐近稳定.从图5 和图6中可看出，系统的状态量x2与估计量x^2的误差e2亦逐渐收敛于0，则误差e2也是全局渐近稳定.最终可以得到系统的状态误差是全局渐近稳定的.

对于楼宇恒压供水控制系统的故障诊断，是在设计H∞观测器的基础上，产生残差信号re（t），并通过设置阈值来判断系统是否发生故障.然而在实际供水控制系统中，如果阈值太小或者太大，检测结果将不太清晰，为了更好地检测到故障信号，所以将阈值设置为1，阈值逻辑故障诊断仿真如图7 所示.

图7 阈值逻辑仿真

从图7 中可以看出，对于楼宇恒压供水控制系统，当残差信号re（t）超过所设阈值而且继续增长时，说明系统发生了故障.因此，也证明了基于观测器的方法能检测出楼宇恒压供水控制系统执行器故障的发生.

5 结 论

本文为了对楼宇恒压供水控制系统中的执行器故障进行检测，设计了全维观测器，并且得到系统状态误差是全局渐近稳定的，最终得到了状态误差和状态估计误差的关系.利用H∞观测器解决了阈值的设计问题，并且引入了解耦合的方法来解决干扰解耦问题，通过产生残差信号re（t），对系统的故障进行诊断.最后利用MATLAB 对系统进行仿真，得到了如图7 的仿真图，当残差信号re（t）超过所设阈值而且继续增长时表明系统发生了故障，从而验证了本文所提方法是有效的.