面向电力变压器油中溶解气体的卷积神经网络诊断方法

裴小邓，罗 林，陈 帅，王 乔

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

电力变压器是电力系统中关键电气设备之一，一旦变压器因故障而停止工作，将会对整个区域的生产生活造成不可估量的损失。因此，实时识别电力变压器的运行状态是非常必要的[1]。电力变压器在实际运行条件下受电气应力、机械应力和热压力等因素的影响，其绝缘材料与变压器油会发生缓慢的化学变化，进而放出CO2、CO 气体以及生成某些碳氢化合物（CH4、C2H6等）溶解在油中。当变压器发生故障时，将加速这些化学反应的进行，所生成的化合物种类及比例与放电、放热等故障有着密切的联系[2]。

基于DGA 的电力变压器故障诊断方法主要分为传统诊断方法和人工智能诊断方法。传统诊断方法主要有特征气体法和比值法（包括IEC 三比值法、改进的IEC 三比值法）。虽然这些方法便于工程应用，但是编码并不完备，对于某些故障很难找到与之对应的编码，因此诊断的准确率较低。人工智能诊断方法主要包括模糊理论[3]、专家系统[4]、神经网络[5]、支持向量机[6]等。虽然这些方法取得了较好的应用效果，提高了故障识别率，但同时存在着一定不足。模糊理论诊断法隶属函数难以确定，需要大量的实际故障数据；专家系统诊断法需要大量的专家经验，获取到的经验难以表达，推理能力较弱；神经网络诊断法存在易陷入局部最优、收敛速度慢、泛化能力差等缺点；支持向量机诊断法在本质上属于二分类问题，处理多分类问题时需要经历“一对一”或“一对多”等复杂的过程，核函数和正则化参数选择困难。

随着机器学习的发展，深度学习的发展推动了人工智能技术在变压器DGA 故障诊断方面的诸多应用，如深度置信网络（Deep Belief Network，DBN）[7]、深度自编码网络(Deep Auto -Encoder Network，DAEN)[8]、卷积神经网络(Convolutional Neural Network，CNN)[9]。文献[10]提出了一种基于深度置信网络构建变压器故障诊断模型，利用快速歧化算法加快了网络收敛速度，在诊断的准确率上较BPNN 和SVM 有了提升。文献[11]提出了一种基于贝叶斯正则化深度信念网络的电力变压器故障诊断方法，克服了传统的DBN 方法在大量无标签样本的情况下才能得到较高准确率的缺点。文献[12]提出了一种基于深度自编码网络的电力变压器故障诊断方法，解决了一些样本数据缺少标签的问题，但是该方法需要大量的预训练样本，在预训练样本数据较少时，诊断的效果并不理想。文献[13]提出了一种基于卷积神经网络的变压器故障诊断方法，虽然克服了一些浅层机器学习方法存在的问题，但是池化类型和网络深度的选择并未说明，卷积网络强大的特征提取能力并未得到展示。

本文提出了一种基于卷积神经网络的变压器故障诊断方法，利用卷积层提取特征和池化层强化重要特征的能力来解决特征提取和过拟合的问题，达到提高诊断准确率的目的。

1 卷积神经网络的基本原理

一个完整的卷积神经网络一般是由输入层、卷积层、池化层、展开层、全连接层、输出层组成,其中卷积层和池化层是整个网络的核心。

1.1 卷积层

卷积层是通过使用卷积核对上一层的部分区域进行卷积运算，提取出相应的特征信息。卷积层最重要的两个特点是稀疏连接和权值共享，这两点也是卷积神经网络和普通的神经络本质上的区别。稀疏连接和全连接的不同之处在于卷积层中的神经元只与上一层的部分神经元相连，权值共享的优点在于特征提取时可以不考虑局部特征的位置，同时可以有效地减少卷积层网络参数的数量，从而降低因参数过多而发生过拟合的几率。全连接、稀疏连接、权值共享示意图如图1 所示。

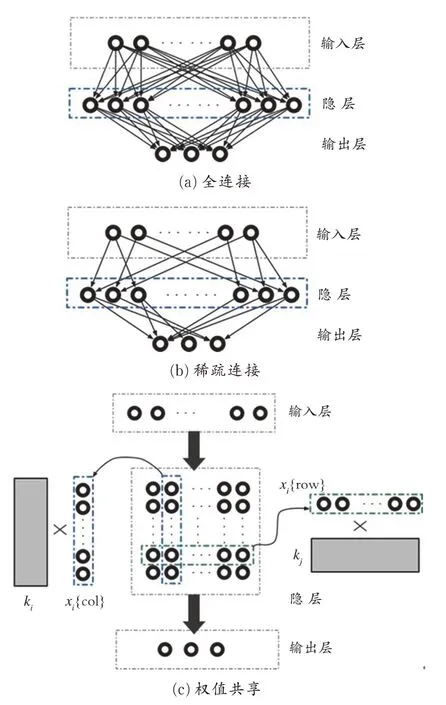
图1 全连接、稀疏连接、权值共享示意图

卷积层的输出结果为：

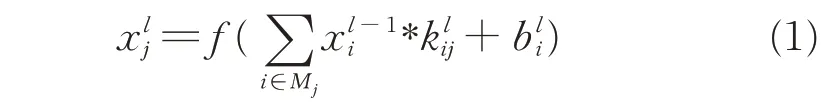
1.2 池化层

卷积层提取到的特征在传入下一层之前，可以对其进行处理，池化是最常用的处理方式。通过池化层的处理，卷积层提取到的特征维度得到有效的压缩，可以减少网络中参数的数量，网络的计算量得到降低，同时也降低网络发生过拟合的几率。池化有最大池化和平均池化两种方式，最大池化是对某个区域的特征取最大化的操作，可以滤去一些不重要的特征信息。平均池化是对某个区域的特征进行平均化的操作，对一些不重要的特征信息并不像最大池化那样完全滤去，而是淡化，以此来强化那些重要的特征信息。由此可见，模型经过池化处理后，其抗干扰能力和稳定性都得到加强。

池化层的输出结果为：

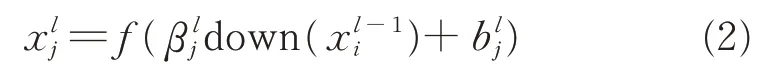
1.3 Softmax 回归模型

本文采用Softmax 回归模型。Softmax 回归模型是Logistic 回归模型的推广,常用于求解多分类问题。假设训练集为{(x(1)，y(1))，(x(2)，y(2))，…，(x(m)，y(m))}，其中x(i)∈Rn+1，y(i)∈{1，2，3，4，…，k}，当输入样本为x 时，可由激励函数hθ(x)求出样本属于任意类别时的概率p(y=j|x)。假设函数将要输出一个k维的向量来表示k 个估计的概率值，这些向量元素之和为1。激励函数可表示为：

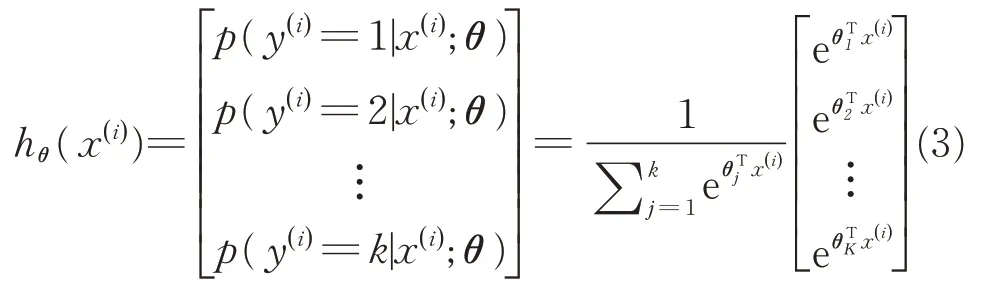
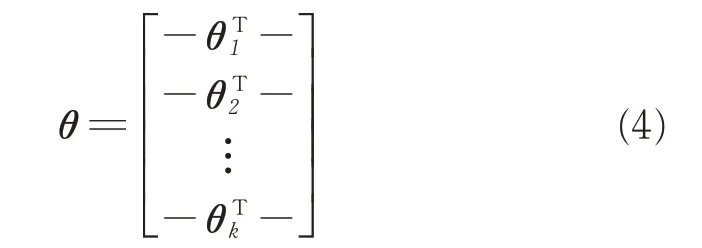
式中，θ1,θ2,…,θK∈Rn+1为模型参数项是对概率分布进行归一化处理，使所有概率的和等于1。将θ 用一个K×(n+1)的矩阵可表示为：

接下来对Softmax 回归代价函数进行分析。代价函数J(θ)见式（5）。在式（5）中，1{·}是指示性函数，运算规则为：1{表达式的值为真}=1，1{表达式的值为假}=0。

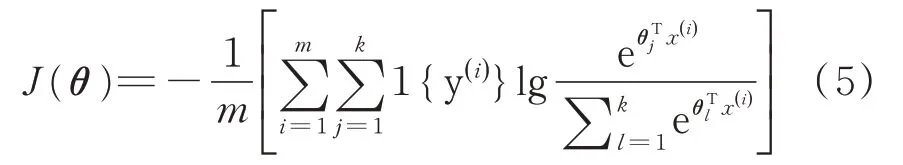
将样本x 分类，分为第j 类的概率为：

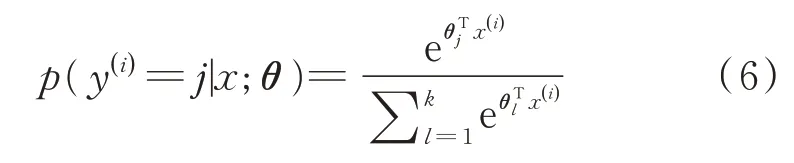
在实现softmax 回归算法时,通过在式中添加一个权重衰减项对过大的参数值进行惩罚。回归代价函数公式将表示为：

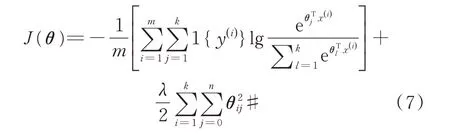
增加权重衰减项后，代价函数成为一个凸函数，这样能防止优化过程中陷入局部收敛，得到最优解。为对其进行优化，需要计算J(θ)的导数，其梯度公式为：

式中，∇θjJ(θ)为向量，第l 个元素是J(θ)对θj第l 个分量的偏导数。利用梯度下降法对代价函数J(θ)进行最小化。每次迭代过程中都需要对参数进行更新。

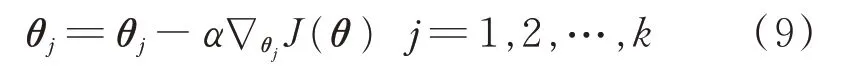
式中，α 为学习率。

2 卷积网络诊断模型的搭建

2.1 输入和输出向量的选择

根据《变压器油中溶解气体分析和判断导则》可知，变压器发生故障状态时共有氢气（H2）、甲烷（CH4）、乙烷（C2H6）、乙烯（C2H4）、乙炔（C2H2）、一氧化碳（CO）、二氧化碳（CO2）七种气体存在，本文选取其中五种气体（H2、CH4、C2H6、C2H4、C2H2）作为变压器故障诊断的输入特征向量。选取正常N、局部放电PD、低能放电D1、高能放电D2、中低温过热T1、高温过热T2 作为卷积神经网络的输出向量。

2.2 数据预处理

本文将每种气体（共五种）体积与气体总体积之比作为卷积网络诊断模型的输入，按照式（10）做规范化处理。

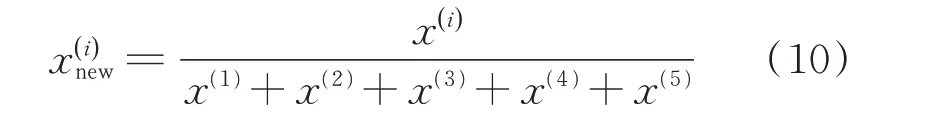
2.3 变压器故障编码

对六种变压器故障类型进行二进制编码，结果如表1 所示。

2.4 CNN 模型诊断结构图

卷积神经网络处理的数据一般是m×n 的二维格式，但是本文用于诊断变压器故障的数据是m×1 的一维格式，所以采用一维卷积神经网络搭建诊断模型。由于数据维度小，只搭建了单层和双层两种诊断模型。

表1 变压器故障类型编码

CNN 模型诊断结构如图2 所示。输入层的大小为5×1，因此卷积层C1卷积核的大小有1×1、2×1、3×1、4×1 四种选择。为了体现卷积层稀疏连接的优势，C1层只选择卷积核大小为2×1、3×1、4×1三种进行实验。

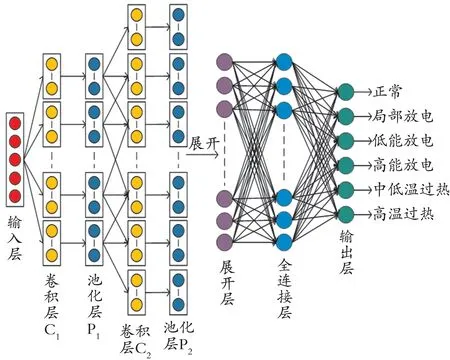
图2 CNN 模型诊断结构

2.4.1 单层卷积诊断模型 当卷积层有K 个大小为m×1(m=2,3,4)的卷积核，可以提取到K 个大小为(6-m)×1 的特征图。当池化层的大小为2×1，可以得到K 个大小为的 特征图，经展开后共获得K(6-m)/2 个特征。

2.4.2 双层卷积诊断模型

(a)当卷积层C1有K1个大小为2×1 的卷积核，可以提取到K1个大小为4×1 的特征图。当池化层P1的大小为2×1，可以得到K1个大小为2×1 的特征图。当卷积层C2有K2个大小为2×1 的卷积核，可以提取到K2个大小为1×1 的特征图，当池化层P2的大小为1×1，可以得到K2个大小为1×1 的特征图，经展开后共获得K2个特征。(b)当卷积层C1有K1个大小为3×1 的卷积核，可以提取到K1个大小为3×1的特征图。当池化层P1的大小为2×1，可以得到K1个大小为2×1 的特征图。当卷积层C2有K2个大小为2×1 的卷积核，可以提取到K2个大小为1×1 的特征图。当池化层P2的大小为1×1，可以得到K2个大小为1×1 的特征图，经展开后共获得K2个特征。

全连接层的神经元个数设为32，卷积层和全连接层的激活函数为Relu。为防止过拟合，在全连接层后面使用Dropout 技术，比率设为0.2，学习率设为0.000 1，迭代次数设为2 500。

3 实验分析

本文变压器故障实验基于python3.7 语言环境，在操作系统为Windows10 家庭中文版(64 位)、CPU为Intel(R) Core(TM) i5-5200U (2 201 MHz)、内存为8 G 联想80FA 电脑上完成。

3.1 样本数据的选取

本文从相关文献中一共获取了393 条完整的变压器DGA 数据进行实验。将故障样本按照7∶3 的比例划分为训练集和测试集。训练集和测试集的分布状况如表2 所示。

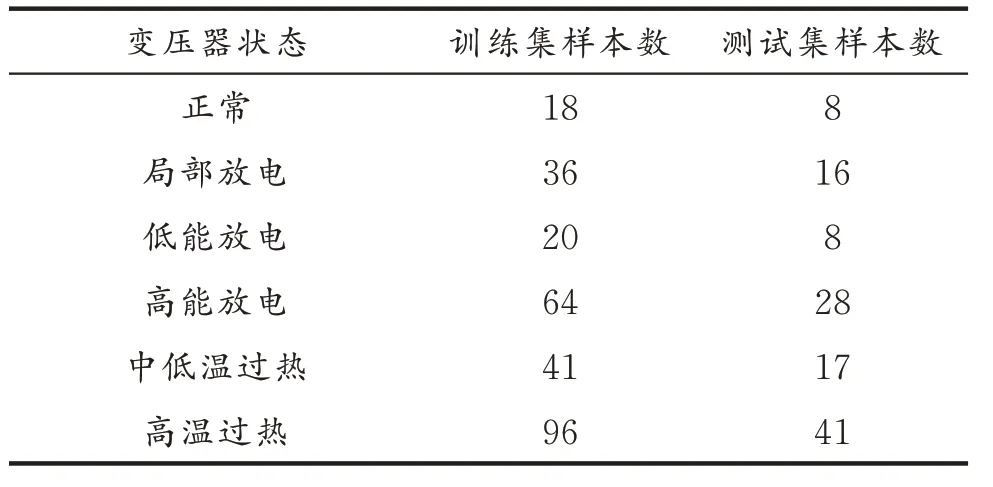
表2 训练集和测试集的分布情况

3.2 卷积核数目对模型性能的影响

为了保证实验的准确性，将卷积网络其他参数的设置保持一致（包括卷积核大小、池化类型的选择、全连接层单元数目、学习率、Dropout 比率等参数）。卷积核数目对训练集准确率、测试集准确率以及训练损失的影响如图3 所示。

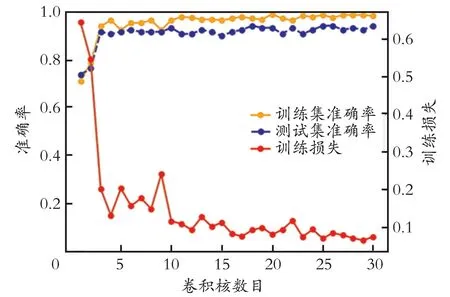
图3 卷积核数目对训练集准确率、测试集准确率以及训练损失的影响

从图3 可以看出，当卷积核数目从1 增加到3时，训练集准确率和测试准确率不断提高，卷积核数目从3 增加到30 时训练集准确率和测试准确率趋于平稳。当卷积核数目从1 增加到4 时，训练损失大幅减少，卷积核数目从4 增加到17 时总体上为下降趋势，卷积核数目从17 增加到30 时有小幅度变化，总体是趋于平稳的。由此可以得出，随着卷积核数目的增加，训练集和测试集的准确率并不会一直增大，训练损失也不会一直减小。为了使训练集和测试集准确率高，同时使训练损失小，卷积核数目为17 时最为合适。

3.3 卷积核大小对模型性能的影响

在卷积核数目为17、其他参数保持相同的情况下，选择卷积核大小为2×1、3×1、4×1 来测试卷积核对模型性能的影响，从训练损失和训练准确率两方面来比较说明。不同卷积核的训练损失及训练集准确率迭代图如图4 所示。

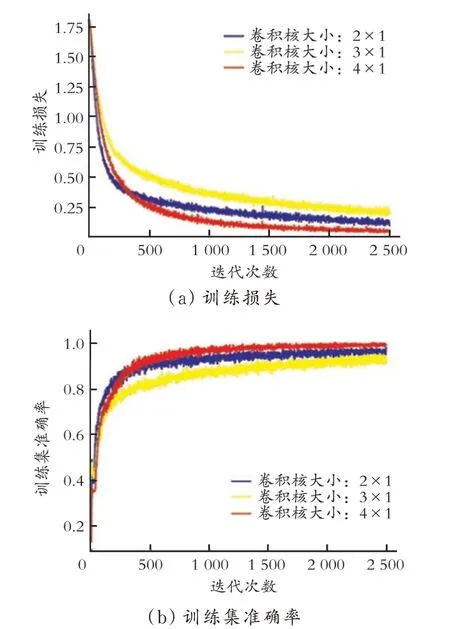
图4 不同卷积核的训练损失及训练集准确率迭代图

从图4 可以看出，当卷积核大小为3×1 时，训练损失最大，训练集准确率最低；当卷积核大小为4×1 时，训练损失最小，训练准确率最高。该实验证明，并不是卷积核越小训练集准确率越高，训练损失越小。为了使训练集准确率高同时训练损失小，卷积核大小为4×1 最为合适。

3.4 池化层对模型性能的影响

分别测试最大池化和平均池化对模型性能的影响，选择卷积核数目为17，卷积核大小为4×1，池化层大小为2×1，其他的参数保持相同。不同池化层下的训练损失、训练集准确率、测试集准确率如表3 所示。从表3 可以看出，最大池化的训练集和测试集准确率更高，训练损失更小，证明最大池化使模型的诊断性能更为优秀。

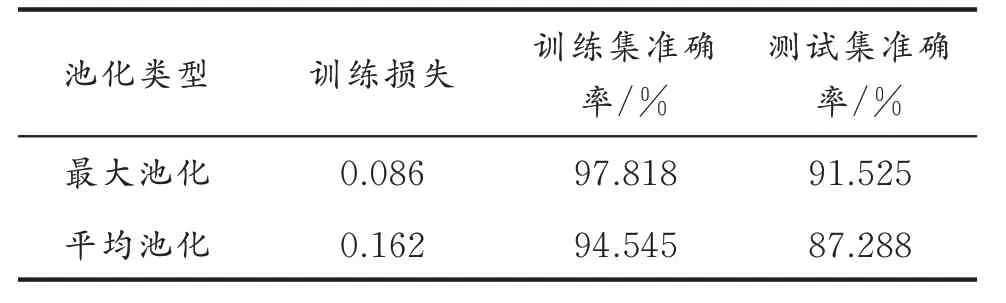
表3 不同池化层的训练损失、训练集准确率、测试集准确率

3.5 学习率和Dropout 比率对诊断结果的影响

为了优化模型性能，测试学习率和Dropout 比率对变压器诊断结果的影响，结果如图5 所示。

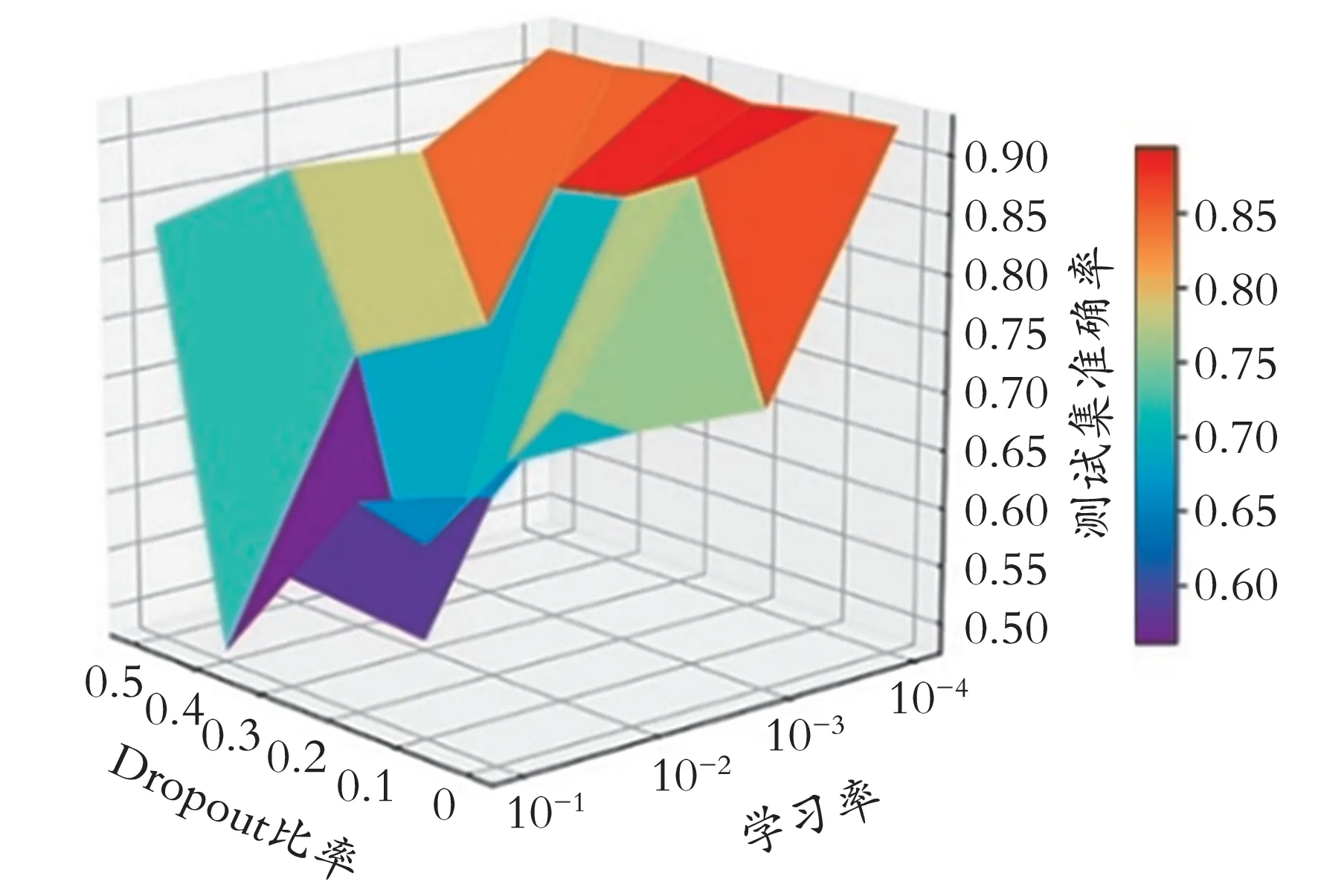
图5 学习率和Dropout 比率对变压器诊断结果的影响

从图5 可以看出，当Dropout 比率一定时，诊断的准确率会随着学习率的减小而增加。当学习率为0.100 0、0.010 0、0.001 0 时，Dropout 比率对诊断结果影响较大，当学习率为0.000 1 时，Dropout 比率对于诊断结果没有影响。实验结果表明，当学习率选择合适时，模型并不会发生过拟合现象，证明了卷积层的稀疏连接和权值共享能够有效地防止过拟合，同时也证明了池化层增强了模型的稳定性。

3.6 网络深度对模型性能的影响

为了测试网络深度对模型诊断性能的影响，本实验将对单层和双层（单个卷积层加上单个池化层为一层网络）卷积诊断模型的性能进行对比。单层模型参数选择实验最佳参数，即卷积核数目为17，卷积核大小为4×1，池化层选择最大池化。双层模型有2 种方式，单层卷积和双层卷积诊断模型性能如表4 所示。卷积层中17-4×1 表示卷积核数目为17，卷积核大小为4×1，池化层中2×1表示池化层大小为2×1，池化类型同样选择最大池化。其余的参数单层和双层保持一致（从结构上讲，双层是单层网络的复制，仅设定单层网络初始参数）。从表4 可知，单层和双层的训练损失、训练集准确率、测试集准确率几乎相同，证明了单层和双层诊断模型的性能相同，这是由于DGA数据结构简单，受网络深度影响较小。

表4 单层卷积和双层卷积诊断模型性能

3.7 实验对比

从混淆矩阵、ROC 曲线、PR 曲线等多个方面来比较CNN、SVM、BPNN 模型诊断性能。CNN、BPNN、SVM 的混淆矩阵如图6 所示。从图6 可以看出，CNN 模型对于正常、低能放电、高能放电、中低温过热、高温过热状态预测上效果较好，局部放电状态的预测效果一般；BPNN 模型在高能放电、中低温过热、高温过热状态的预测效果较好，在正常、局部放电、低能放电状态的预测效果较差；SVM模型在高能放电、中低温过热、高温过热状态的预测效果较好，在局部放电状态的预测效果一般，在正常、低能放电状态预测效果非常差。尤其是低能放电状态，SVM 模型预测准确率为0，BPNN 模型预测准确率为50%，而CNN 模型预测准确率为100%。实验证明了CNN 模型的分类性能要明显优于BPNN 模型和SVM 模型。

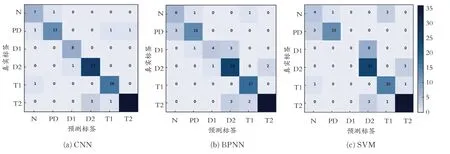
图6 CNN、BPNN、SVM 的混淆矩阵

不同模型的训练集和测试集准确率如表5所示。

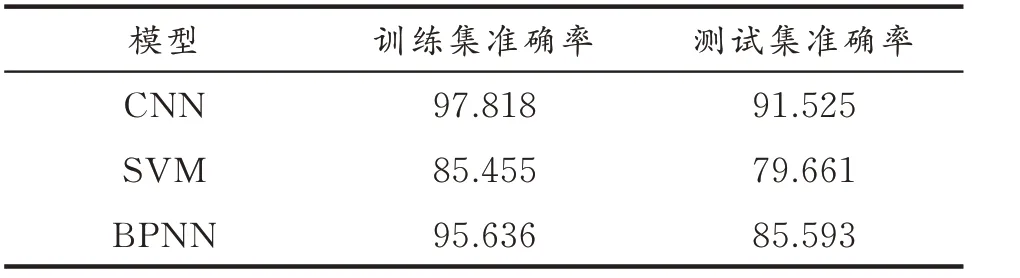
表5 不同模型的训练集和测试集准确率 %

从表5 可以看出，CNN 模型的训练集准确率和测试集准确率都超过了90%，明显高于SVM 模型和BPNN 模型，这是由于CNN 模型特征提取能力要比SVM 和BPNN 强。SVM 模型训练集和测试集的准确率都不高，说明SVM 模型在多分类问题上分类能力一般。BPNN 模型虽然训练集准确率高达95.636%，但是训练集的准确率只有85.593%，说明BPNN 模型的泛化能力较差，容易发生过拟合。

不同模型的ROC 曲线如图7 所示。从图7 可以看出，CNN模型ROC 曲线AUC 值高达0.99，比SVM 模型AUC 值高0.02，比BPNN 模型AUC 值高0.01，AUC 值接近的原因是由于样本不平衡造成的，AUC 值受样本数量影响较大，从混淆矩阵中可以看出BPNN、SVM 模型在高能放电、高温过热状态预测结果非常出色，最终导致AUC 值接近。但是，CNN 模型的分类和泛化能力比SVM 和BPNN模型要优秀。

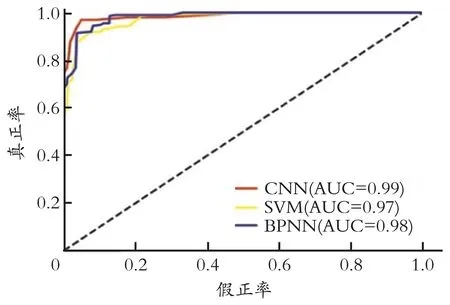
图7 不同模型的ROC 曲线

PR 曲线跟ROC 曲线相比，AUC 的值受样本不平衡影响较小。不同模型的PR 曲线如图8 所示。

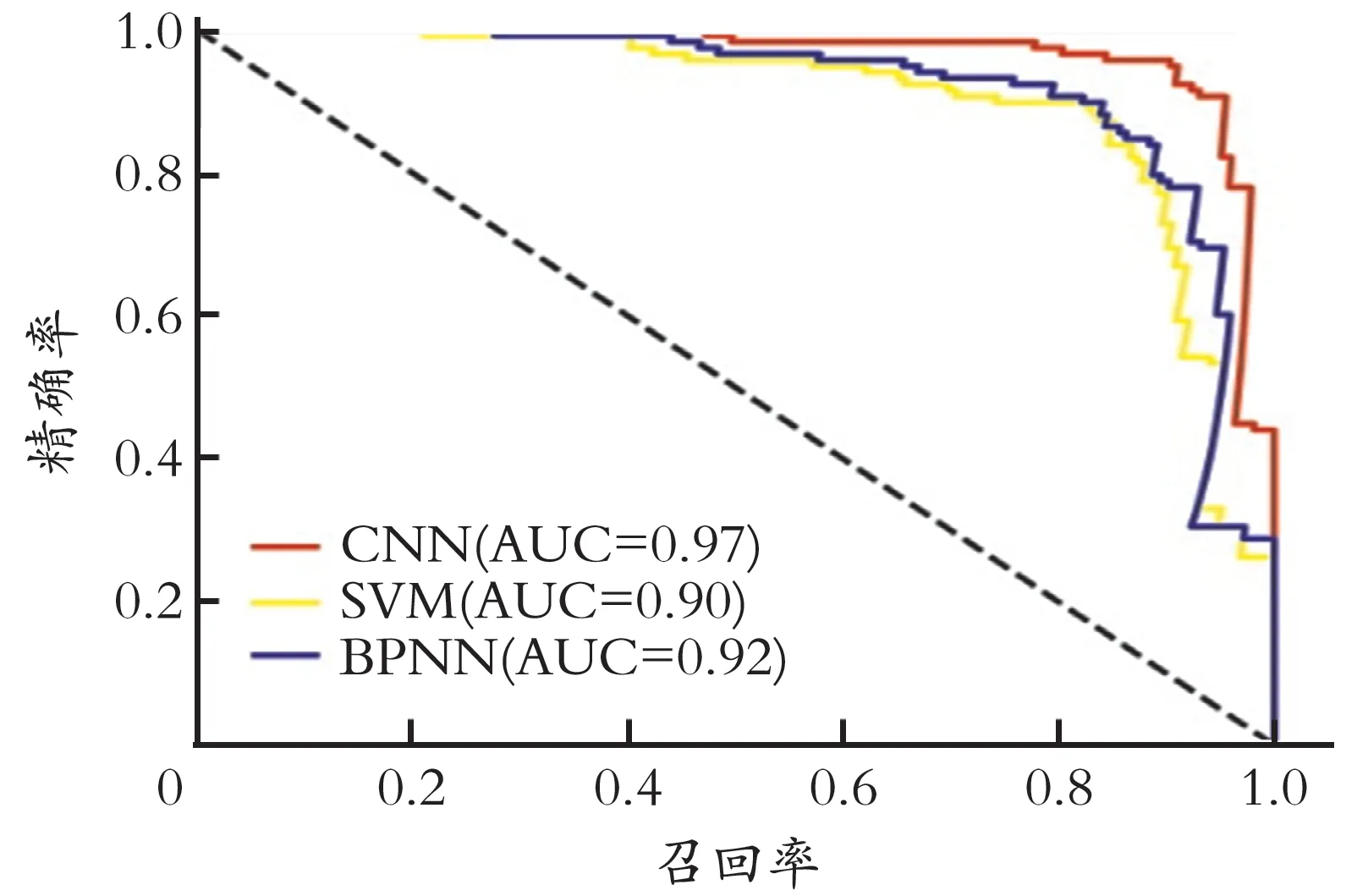
图8 不同模型的PR 曲线

从图8 可以看出，CNN 模型PR 曲线AUC 值高达0.97，比SVM 模型AUC值高出0.07，比BPNN模型AUC 值高出0.05,证明CNN 模型的泛化和分类能力更为优秀。

3.8 特征可视化

CNN 模型诊断准确率高的原因之一在于它强大的特征提取能力。为了验证CNN 模型强大的特征提取能力，采用t-SNE（t-Distributed Stochastic Neighbor Embeding）技术，把CNN 模型提取到的高维特征映射成二维特征，并以散点图的形式可视化出来。首先把CNN 模型的全连接层提取到的393个样本的三十二维特征提取出来，然后利用t-SNE技术将393 个样本的三十二维特征降为二维并展示出来。CNN 模型特征可视化如图9 所示。从图9 可以看出，相同的类聚集在一起，不同的类有一定的距离，聚类的准确率在98%以上，说明CNN 模型提取到的特征可分性好，证明CNN 模型有着优秀的特征提取能力。

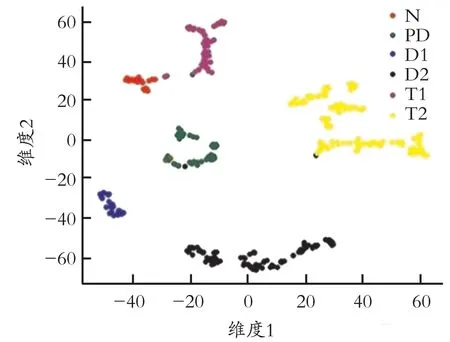
图9 CNN 模型特征可视化

4 结 论

在变压器诊断领域，浅层机器学习诊断方法虽然在诊断的精度上较传统的方法有所提升，但是还存在着一些缺点，为克服这些缺点，构建基于卷积神经网络的变压器故障诊断模型。通过混淆矩阵、ROC 曲线、PR 曲线多方面实验验证，基于卷积神经网络的变压器故障诊断方法跟支持向量机、BP 神经网络相比，特征提取和泛化能力更强，诊断的准确率更高。实验结果表明，双层卷积网络模型诊断准确率不一定比单层的高，卷积核的数量并不是越多越好，卷积核的尺寸并不是越小越好，因此卷积网络的深度、核数目、核大小要根据数据的实际情况来选择。对于池化层的大小和全连接层神经元数目的选择并未讨论，这也是下一步研究的重点。