彭罗斯镶嵌与建筑生成探讨

张旭颖，靳铭宇

(北方工业大学 建筑与艺术学院，北京 100144)

1 引言

镶嵌图形在建筑中已被广泛应用，但人们对其数学原理知之甚少，对其在建筑中应用方式也缺乏创新，本文从数学理论在建筑中应用的层面，通过对镶嵌图形原理的论述与对建筑中镶嵌理论实际应用案例的分析，以彭罗斯镶嵌为重点，展现数学理论对建筑生成的创新方法与意义，为建筑生成提供借鉴。

2 镶嵌图形的原理与特点

图形的拼接是一种常见的装饰，从中国古建的门窗格栅到现代墙壁上的瓷砖，从伊斯兰世界的地毯到中国的刺绣，美轮美奂的镶嵌图形以其特有的几何魅力在装饰界深深吸引着人的注意。镶嵌图形在建筑装饰中的应用历史悠久。数学几何作为装饰元素经久不衰，研究其内在原理，剖析镶嵌的基本结构，对镶嵌在装饰上的应用会有更深层次的理解。

空间镶嵌的形式是指依据某种对称性秩序的空间规律，重复排列某一“单元形”，使其能够不留任何缝隙且完全无重叠地填满自身所在的整个空间，在二维空间中的镶嵌又叫做图形的密铺[1]。根据镶嵌所主导的对称操作的不同，镶嵌又可以分为两大类：由平移所主导的周期性镶嵌和由平移与旋转共同主导的准周期镶嵌[2]。

这些特殊的图案形成来源于一个思考：如何用一种或几种图形来铺满整个平面？显然，正方形、正三角形和正六边形是可以进行平面的密铺的，它们的内角分别为90°、60°和120°，以一个角点为拼接点的话可以铺满360°，这些由平移主导的镶嵌图案就是被称为周期性镶嵌的平面图形的密铺；而正五边形在进行平铺时，不能做到无缝拼接，因为五边形的每个角的度数为108°，如果三个五边形进行拼接，那么三个五边形的角度之和为324°，如果4个五边形进行拼接的话，那么四个角的度数之和为432°，均不等于360°，因此，只用单纯的正五边形无法进行平面的无缝的周期性平铺，见图1。

但是，如果采用另一种形状如来补全正五边形拼接图案的缺口的话，即可得到密铺的平面。实际上，若采用多种形状的瓷砖组合，就能得到无穷尽的密铺方案。这种方法得出的图案与正方形所密铺的图案又有所不同，正方形所组成的图案具有平移对称性[3]，它由平移操作所主导，可以通过图形平移得出，是周期性的，而采用多种形状组合的图案则可能是非周期性的，它并不能通过一个单元重复平移得到。

图1 正多边形的密铺

这就使得平面密铺图案有了更多的变化。不同于对称与重复的美感，非周期平面图形密铺带来了一种充满数学奥妙的图案，它看似有规律却找不出重复的单元，图形在平面上不断拼贴却永没有重复的图案，如同无理数一样永不循环，但相比与直白的数字又多了些几何的美感。对于建筑师来说这是一种新的美学，数学家则致力于研究采用更少的图形得出非周期性的平面图形密铺。

3 准周期镶嵌

1973年，英国的数学家和物理学家罗杰·彭罗斯(rogerpenrose)提出了一种具有5次旋转对称的拼图。他发现正五边形可以分割为6个小的正五边形和5个三角形，对小五边形进行再一次分割后就产生了一个五角星形和一个类似帆船的形状。利用这四个形状，就能不重复地对平面进行密铺。这就是由平移与旋转共同主导的准周期镶嵌，见图2。

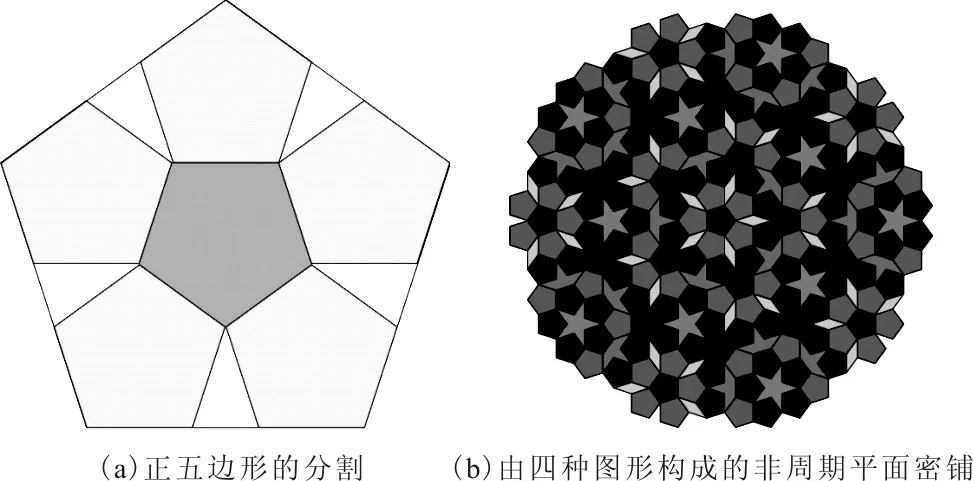
图2 P1型彭罗斯镶嵌

第二年，彭罗斯对这些形状进行了修改，只运用了两种不同的图案，就创造出了一种新型的拼接方式。他将一个菱形分割成两部分，这两种图案分别形象地被称为“风筝”和“飞镖”，见图3。

图3 a“风筝”，b“飞镖”

从图中可以看出，一个内角分别为72°，108°，72°，108°的菱形，由上图中的分割方法分割成飞镖形和风筝形，飞镖形的内角为分别为36°，72°，36°和216°，风筝形的内角分别为72°，144°，72°和72°。这些角的°数，都是36°的整数倍，这几种度数通过不同的组合方法，都可以组成360°，而且，菱形的四条边具有等长性，且分割出的飞镖和风筝的边都有互相对应的等长的边。边缘可以完全对应，角度也可以完全对应，因此，飞镖形和风筝形可以进行平面的无缝拼接，见图4、5。

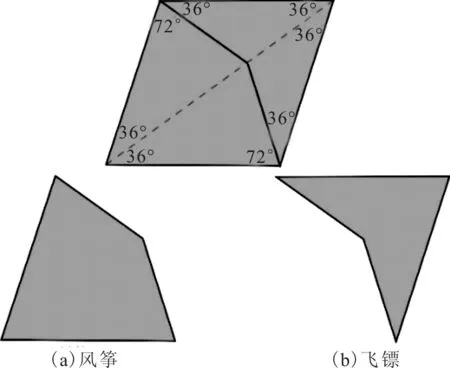
图4 P2型彭罗斯镶嵌，由“风筝”和“飞镖”组成

图5 P2型彭罗斯镶嵌

彭罗斯创造出的第3种非周期平面图形密铺方案是由一个36°、72°菱形和一个72°、108°菱形构成的。这三种镶嵌方式本质上都是五重旋转[4]，只是表现形式不同。这些镶嵌方式以发现者彭罗斯的名字进行命名，被称之为“彭罗斯镶嵌”，它们都与数学中的黄金分割[5]有关。彭罗斯发明的这种图案的拼接方式，实际上是把人工发明的黄金比例的数学概念与日常生活中的数学关联到了一起。第一种类型的彭罗斯镶嵌是通过五边形的不断膨胀不断延伸而成，它的膨胀率为黄金分割值的平方，第二种彭罗斯镶嵌中，风筝图案和飞镖图案的数量之比等于黄金分割值；第三种的基础图形为菱形，经过一次延伸后，面积为原来的黄金分割值的平方倍，它们都和黄金分割有着密不可分的联系[6]，这也与建筑设计中常见的黄金比例不谋而合，见图6。

图6 P3型彭罗斯镶嵌

4 彭罗斯镶嵌在建筑中的应用

彭罗斯镶嵌从其诞生开始，其所具有的独特结构就引起了多方关注，它不仅使彭罗斯在数学界广为人知，在装饰与艺术界也被许多人所青睐。设计师们被准周期结构所具有的随机的、不重复的美感所吸引，这种“有趣”的图形让人不禁仔细观察，摆脱拼贴的“一次性”的吸引力。

墨尔本皇家理工学院的斯托雷厅改造项目就采用了彭罗斯镶嵌作为其建筑视觉主题，设计师对彭罗斯镶嵌进行了立体化处理，使彭罗斯镶嵌表现出浮雕一般的效果，两种菱形搭配两种颜色的灯光，成功营造了一种多层次、充满科学神秘感的神奇氛围。见图7。

牛津大学数学系安德鲁·威尔斯大楼门前则采用了P3型彭罗斯镶嵌作为地砖。铺路由两块不同的菱形花岗岩铺设，被饰以不锈钢圆弧的花岗岩砖永不重复地排列下去，以独特的方式展现建筑中数学的魅力，见图8。

图7 墨尔本皇家理工学院的斯托雷厅

图8 牛津大学数学系门前铺路

5 结语

彭罗斯镶嵌还应用在了多个地方。西澳大利亚大学bayliss大楼中庭的地板、芬兰赫尔辛基市keskuskatu街的行人路都采用了彭罗斯镶嵌图案(图9)。这些图形将数字的魅力带入装饰，以严谨又随机的秩序创造出千姿百态的图形，以无规律可言的方式在平面上拼接，产生了不可思议的变化，令当时的人们啧啧称奇。彭罗斯镶嵌对建筑装饰界带来了新的美学，至今仍以独特的魅力吸引着人的目光。

图9 芬兰赫尔辛基市keskuskatu街行人路