失谐设计在叶片自激振动减振中的应用

刘一雄，陈育志，丛佩红，伊 锋，杜少辉

（中国航发沈阳发动机研究所，沈阳110015）

0 引言

航空发动机压气机转子叶片屡次发生高周疲劳断裂故障，且叶片的振动模式不是通常存在的整阶次强迫振动，而是由于气流攻角等因素改变，引发气动弹性不稳定现象，进而导致叶片产生非整阶次高振幅的自激振动[1]，自激振动一旦发生，叶片会剧烈振动，在短时间内断裂，后果极其严重，因此有必要开展气流诱导叶片自激振动抑制技术研究。工程中常见的自激振动主要是颤振和非同步振动，非同步振动的发作区域远离经典颤振区，也远离失速区，其振动特征与经典颤振并无差别，抑制手段与颤振类似[2]。

在不改变叶片结构和降低发动机性能的条件下，失谐设计是航空发动机叶片抑制颤振的有效手段。实际上由于受材料不均匀性和加工工艺限制，真实的叶盘结构都是失谐的。国外针对失谐对叶片气动弹性稳定性影响开展了大量研究工作。Whitehead[3]和EWins[4]的研究表明失谐叶片结构对颤振有一定的抑制作用；Kaza 等[5]和Kielb 等[6]深入研究了错频结构对颤振和强迫振动的影响，指出错频可以提高叶片振动系统气动弹性稳定性；Kazawa 等[7]研究了交替错频对平面振荡叶栅颤振特性的影响；Sadeghi 等[8]从振荡叶栅非定常气动响应的角度，研究了叶片相位角失谐和频率失谐对叶栅气动弹性稳定性的影响。中国在失谐对叶片气动弹性稳定性研究方面也进行了较为深入的研究工作。郑赟等[9]采用流固耦合能量法研究了错频对叶片气动弹性稳定性的影响；张小伟等[10]研究了叶片相位角对叶片颤振的影响；付志忠等[11-12]采用影响系数法详细研究了各种错频模式和错频量等因素对叶片气动弹性稳定性的影响规律。另外，一些学者从强迫振动的角度出发，力图降低叶片强迫振动应力。王建军等[13]阐述了失谐叶盘结构振动局部化的基本问题和研究进展；袁惠群等[14-15]基于改进的嵌套遗传算法对叶片进行减振安装优化，以降低强迫振动响应幅值；赵志彬等[16]开展了叶盘结构受迫振动响应特性和主动失谐技术试验研究。上述研究大多需要进行较为复杂的数值计算，在实际发动机叶片错频设计和装配现场叶片安装排布时缺乏可操作性。

本文采用发展的特征值法[17]对某压气机转子叶片进行气动弹性稳定性分析，在此基础上，开展隔离带错频设计对叶片自激振动的减振效果影响研究和试验验证。

1 研究方法和模型

某压气机转子叶片多次发生叶根断裂故障，叶片振动特征与强迫振动不同，主要表现为激振频率不是转速基频的整数倍，出现锁频、锁相现象，整圈叶片的频率锁定在1 阶弯曲频率附近。在转动坐标系中叶片的动频与在静止坐标系中压力脉动频率存在一定关系，符合后行波特征。同时，叶片发生故障的区域与典型失速颤振不同，并未发生在近喘边界，而是发生于共同工作线，且呈现大幅稳定振动。故障现象与文献[2]中提及的非同步振动类似，分析认为其归属于气流诱发的叶片自激振动问题范畴。由于叶片的结构和工作载荷不可改变，不能采用改变叶片固有频率或激振频率等方法进行减振设计，在这种情况下对叶片进行错频设计是最具操作性的减振措施。

采用发展的特征值法，仅考虑由叶片振动引起的非定常气动力，则运动方程为

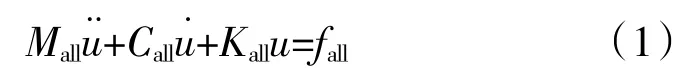
式中：Mall、Call、Kall分别为质量、阻尼和刚度矩阵。

当考虑叶片的前l 阶模态时，第k 个叶片的位移为

式中：Uk为第k 个叶片的前l 阶复数模态振幅向量；φ为适用于所有叶片的前l 阶模态。将式（2）代入式（1）并前乘φT，得到

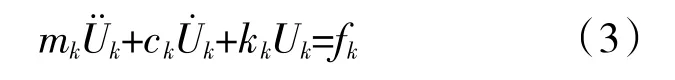
式中：mk、ck、kk分别为第k 个叶片的模态质量、模态阻尼和模态刚度矩阵；Fk为第k 个叶片的模态气动载荷。

叶片的模态气动载荷组成的向量为

式中：m、c、k 分别为叶片的模态质量、模态阻尼和模态刚度矩阵。

假设叶片做简谐振动，振动频率为ω，则模态运动方程为

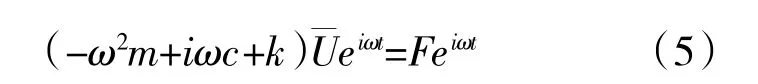
将式（6）代入式（5）可得

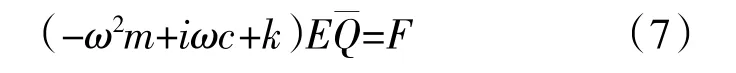
对于一般的振动形式，气动力可以通过单个行波叠加获得，对于任意行波振动，第n 节径的广义气动力可以表示为气动力影响系数an乘以复数模态振幅的线性形式

将式（8）代入式（7）并前乘E 的共轭转置矩阵E*，可得行波坐标系下的振动方程

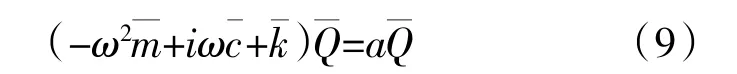
式中：a 为对角矩阵，其对角线元素an为行波坐标系下节径数为n 的气动力影响系数

将式（10）代入式（9）可得

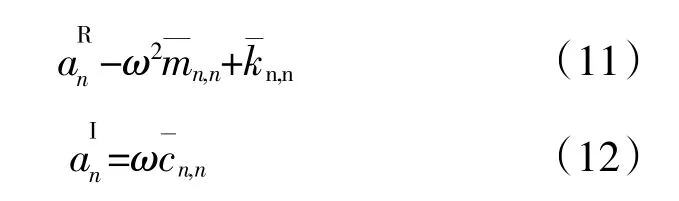
通过将物理坐标系下的振动方程转换到模态坐标系并进一步转换到行波坐标系，得到表征叶片气动弹性稳定性的特征值，以特征值虚部的最小值评估叶片的气动弹性稳定性。特征值法优点是可以采用调整密度或者弹性模量的方式分析不同叶片频率排布对特征值的影响。

某压气机转子叶片的有限元模型和1 阶弯曲模态分布如图1 所示，在计算过程中考虑了榫头对叶片频率和振型的影响。

图1 某压气机转子叶片的有限元模型和1 阶弯曲模态

在非定常流场分析时如果按整圈叶片进行计算会消耗大量计算资源且耗时较长，结合文献[11、17-19]可知，假设叶片在某1 阶模态振荡作用下，只有参考叶片振动，其它叶片不动，则通过在不同叶片间相位角下对所有叶片的非定常气动力叠加，即可获得行波运动形式下的气动阻尼。同时，参考叶片对其它叶片的影响随着距离的增加而迅速减小，如图2 所示。分析认为7 个通道的流体模型即可保证足够的计算精度，所建立的流体模型如图3 所示。

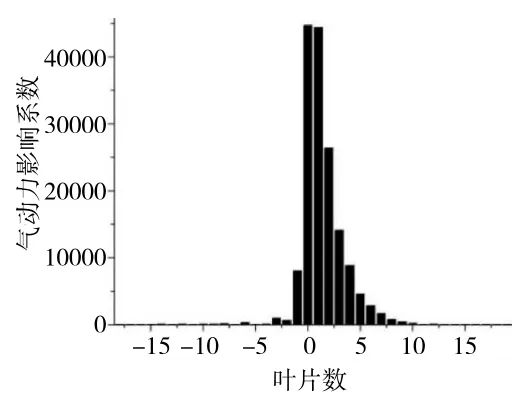
图2 气动力影响系数幅值

图3 7 通道流场模型

2 叶片失谐设计

工程中经常采用频率隔离带的形式来实现错频设计，对频率较低的叶片错频量为5%～10%，对频率较高的叶片错频量一般为3%～5%，通常的频率错频是指叶片静频。

错频设计主要考虑2 方面内容：

（1）频率分布：主要包括隔离带的数量和位置、隔离带之间叶片分布形式设定等；

（2）叶片频差：主要包括隔离带频差、隔离带内叶片之间的频差、整级频差等。

为研究不同的错频模式和错频量对于叶栅气动弹性稳定性的影响，本文主要从隔离带的数量、位置、其内叶片频率分布等几方面开展基于特征值法的某压气机转子叶片的气弹稳定性影响分析。

2.1 谐调叶片气弹稳定性分析

某压气机转子叶片共有38 片，静频为520 Hz，谐调叶片的特征计算值如图4 所示。从图中可见，特征值虚部最小为0.19，根据特征值法的定义，叶片气弹稳定性随特征值虚部的增大而增大，为此本文的主要目标是寻找到合适的错频方案以提高叶片特征值虚部的最小值。

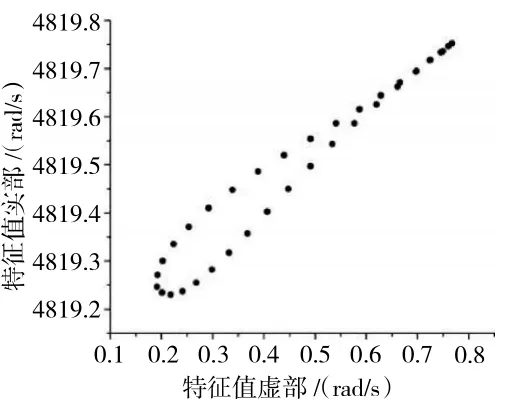
图4 谐调叶片特征值在复平面分布

2.2 隔离带数量影响

在谐调叶片的基础上引入隔离带的概念，主要做法是选择若干频率较高的叶片，将其在周向以一定的规律分布，目的是破坏叶片的循环周期对称性，使得当发生自激振动时，振动系统无法轻易将所有叶片调制到同一频率。

隔离带数量可根据整圈叶片数量调整，隔离带数量为3 时的频率分布如图5 所示。

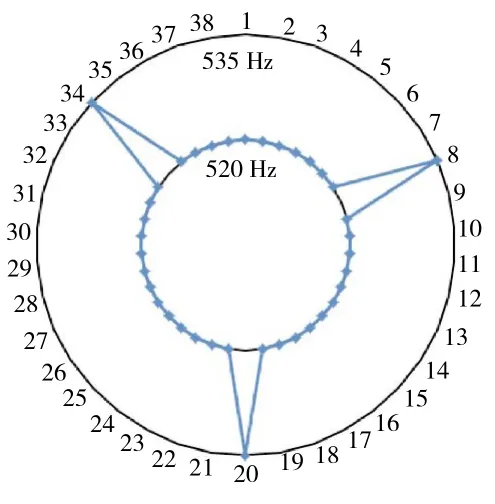
图5 隔离带错频分布

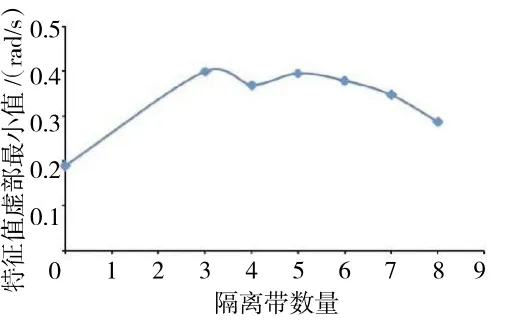
图6 隔离带数量对特征值虚部最小值影响

以某压气机叶片为例，分析了隔离带数量为3～8 时叶片特征值虚部的变化情况，根据工程经验，隔离带与相邻叶片的频差取为3%。不同数量的隔离带对叶片特征值虚部最小值的影响规律如图6 所示。从图中可见，特征值虚部最小值由0.19 增大到0.40，有显著提升，说明引入隔离带能够有效提高叶片的气弹稳定性。同时，隔离带设置时数量不宜太多，否则无法体现隔离作用；奇数隔离带比偶数隔离带作用更为明显。

2.3 隔离带位置影响

隔离带在周向的分布形式对特征值也有一定影响，以5 个隔离带为例，制定了6 种隔离带错频方案，如图7 所示。

计算得到了叶片特征值虚部最小值随隔离带位置的变化规律，如图8 所示。从图中可见，当隔离带在周向均布时，特征值虚部最小值较大，能够有效破坏叶片循环对称周期性，提高系统的稳定性。当隔离带连续排布时，特征值虚部最小值减小，隔离作用不明显。

图7 隔离带不同位置分布

2.4 隔离带内相邻叶片频率分布影响

为了更加有效地提高叶片气弹稳定性，在设置隔离带的基础上，将隔离带内叶片也进行错频，为便于说明，本文均以相邻叶片交叉错频模式开展研究，如图9 所示。真实开展错频设计时，隔离带内叶片不仅限于交叉错频方式。

计算了3～6 个隔离带均布时，隔离带内相邻叶片呈交叉错频时，错频量对特征值虚部最小值的影响，如图10 所示。

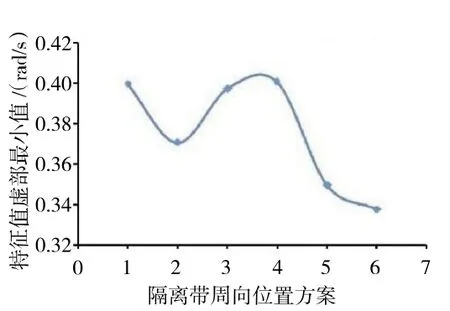
图8 隔离带位置对特征值虚部最小值影响

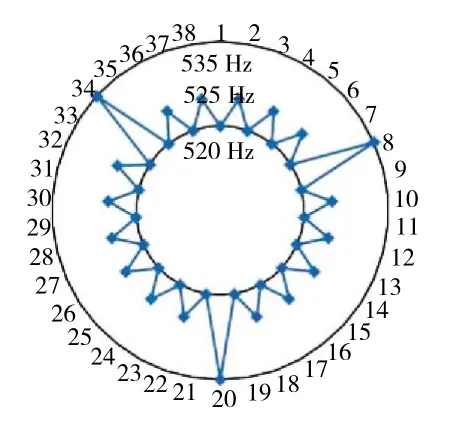
图9 隔离带内叶片交叉错频

3 失谐方案和试验验证

3.1 失谐方案设计

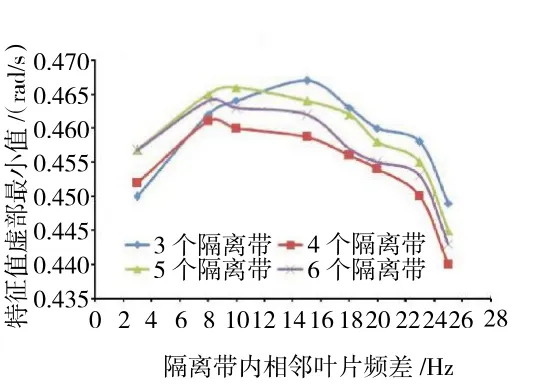
图10 隔离带内相邻叶片频差影响

根据上述研究结论，提出1 种基于隔离带的失谐叶片降低自激振动应力的设计方法，设计流程如图11 所示。其主要思路是对装配现场已有叶片进行频率或质量排序，根据叶片频率大小和叶片数量确定隔离带数量和周向位置，然后确定隔离带内叶片频率排布，最终在达到平衡配重要求的基础上完成叶片失谐方案设计，这种方法充分考虑了装配现场的实际情况，在不需改变叶片结构的基础上，仅通过频率大小即可确定相对较优的安装方案，减振效果好，工程实用性强，应用成本低。

据此设计了某压气机转子叶片失谐方案，如图12 所示。其中，方案1 隔离带不明显；方案2 为3 个隔离带，隔离带内交叉错频；方案3 在方案2 的基础上每个隔离带的交叉错频量不一致；方案4 在方案3的基础上将隔离带扩展为5 个。

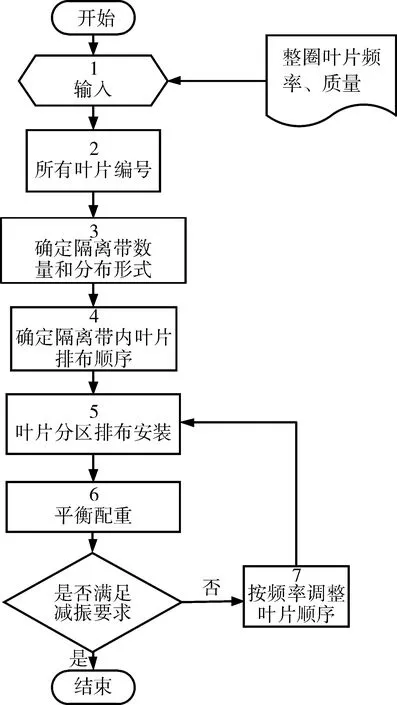
图11 航空发动机叶片失谐减振设计流程

图12 某压气机叶片失谐减振方案设计

计算得到的各种方案下特征值在复平面的分布，如图13 所示。从图中可见，根据制定的叶片失谐方案计算得到的特征值虚部最小值相对于谐调叶片振动系统已经有了明显改善，方案3 和方案4 的特征值虚部最小值基本相当，比方案1 和方案2的大。

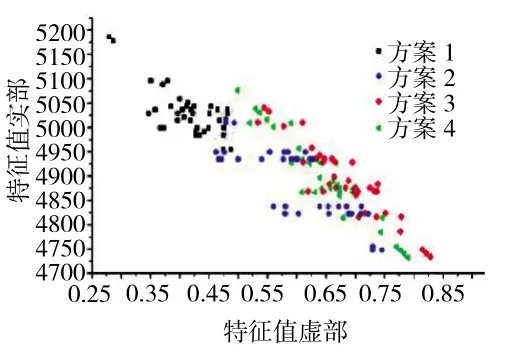
图13 各方案下特征值在复平面分布

3.2 试验验证

为验证隔离带失谐设计方法的实用性及数值仿真的准确性，开展整机动应力测试，布置应变片和光纤监控叶片的振动情况，安装压力脉动传感器用以获取转动坐标系与静止坐标系之间的关系。获得了4 种不同失谐设计方案的实测光纤与特征值虚部最小值之间的关系，如图14 所示。

根据理论分析与试验结果可以发现：

（1）对比方案1 和其它方案的结果可以发现，隔离带不明显时，特征值虚部最小值较小，实测的光纤值也偏高，其对自激振动的抑制能力较差，设置隔离带可有效提高叶片振动系统的稳定性；

（2）方案2 和方案3 结果对比表明，在隔离带内相邻叶片交叉错频的减振效果相对较差，可适当调整隔离带内相邻叶片频率分布以打破对称性从而提高稳定性；

（3）方案3 和方案4 的结果对比表明，对于固定数量的叶片振动系统，隔离带数量有1 个较佳值，本文研究的压气机叶片系统有3 个隔离带时减振效果较好，低于3 个隔离带减振效果不明显，隔离带数量超过该值后气弹稳定不再显著提升；

（4）方案3 中叶片稳定性的理论计算结果最高，而其试验光纤值最低，说明特征值虚部最小值可以有效表征叶片系统的气弹稳定性。

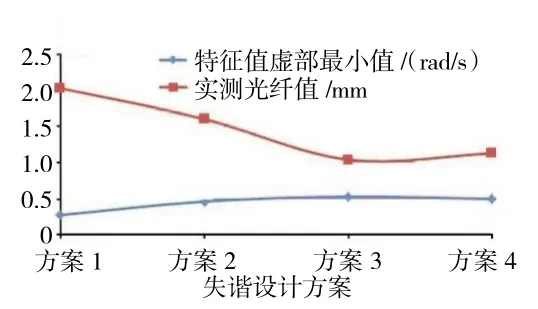
图14 各方案下特征值虚部最小值与实测光纤值

4 结论

本文采用特征值法分析了隔离带错频设计对航空发动机转子叶片自激振动的影响规律，提出了1 种工程可用的隔离带失谐设计方法，得出以下结论：

（1）设置隔离带可以打破叶片振动系统的周期对称性，提高叶片的气弹稳定性，极大改善了由自激振动带来的叶片振动问题。对于固定数量的叶片振动系统，可以通过合理设置隔离带数量和隔离带内相邻叶片频率分布，获得较佳的隔离带减振方案；

（2）特征值虚部最小值与由自激振动引起的振动之间的对应关系较好，可以有效表征叶片系统的气弹稳定性，对于盘榫结构叶片排布安装和整体叶盘结构的失谐设计均具有重要意义。

（3）隔离带错频设计可根据装配现场实际情况进行叶片安装排布，且不需要对叶片结构进行修改，发动机性能不会降低，在某压气机转子叶片减振设计的应用表明，该设计工程实用性强。