基于PCA-LMD 的滚动轴承信号混合特征选取与故障诊断

朱天煦，臧朝平

（南京航空航天大学能源与动力学院，南京210016）

0 引言

航空发动机的滚动轴承长期工作在高温、高压和交变负载条件下，是故障发生频率较高的部件之一[1]。滚动轴承的故障诊断方法研究对航空发动机的维护与减少飞行事故具有重要意义[2]。滚动轴承故障特征往往呈现于振动信号中，可以利用振动信号进行滚动轴承故障诊断。

基于轴承振动信号的故障诊断，主要由轴承振动信号预处理、特征提取及故障诊断3 部分组成。故障特征提取及其故障诊断方法可分为时域法[3]、频域法[4]及时频域法[5]。由于轴承信号往往呈非平稳、非线性[6]，且信号常淹没在噪声当中[7]，如何进行信号的预处理以及提取正确的轴承故障特征是诊断的难点。近年来预处理常用方法有小波降噪[8]、奇异值分解（Singular Value Decomposition，SVD）降噪[9]、主成分分析（Principle Component Analysis，PCA）降噪[10-11]等。本文采用PCA 降噪的方法进行轴承振动信号预处理，旨在研究1 种在PCA 降噪基础上的时域特征提取及故障诊断方法。轴承振动信号的时域特征提取方法包括原始信号的时域特征直接提取、基于自适应分解的轴承振动信号分解及分解得分量的时域特征提取及上述2种方法的组合。基于时域特征的故障诊断多利用智能化的方法实现。Xu 等[12]通过对信号进行混合降噪，将提取降噪后信号LMD 分解得到的能量比特征作为故障特征，通过最小二乘支持向量机（Least Square Support Vector Machine，LSSVM）实现了滚动轴承的故障诊断；刘乐等[13]通过提取经LMD 分解得到的模糊熵作为轴承的故障特征，并通过概率神经网络（Probabilistic Neural Network，PNN）实现滚动轴承的故障诊断；黄文静[14]将原始信号的均值、标准差、峭度、偏度、样本熵和经LMD 分解得到的能量特征结合以表征轴承的真实运行情况，并使用粒子群优化的BP 神经网络进行诊断，获得了不错的结果。尽管上述方法都取得了很好的结果，却忽略了轴承在不同故障深度情况下，不同类型故障信号的时域特征的分析情况；也没有分析故障深度变化对故障分类效果的影响。事实上，故障信号的时域特征随着轴承故障深度的加大而发生变化，但不同故障信号的时域特征变化情况不同，会导致不同故障类型、不同故障深度的时域特征有所重叠，给故障诊断带来困难。

本文在对轴承振动信号进行PCA 降噪处理的基础上，分析了不同故障类型信号经LMD 分解所得PF分量的几种时域特征分别在不同故障深度下，对不同故障类型的分类情况及故障深度变化对所选取的时域信号分类效果的影响；并采用处理小规模数据具有一定优势[15]的支持向量机（SVM）机器学习方法对故障信号进行分类与判断。

1 基于PCA-LMD 混合特征及SVM 的滚动轴承故障诊断方法

本文的轴承故障诊断方法主要由以下4 个步骤组成，其流程如图1 所示。

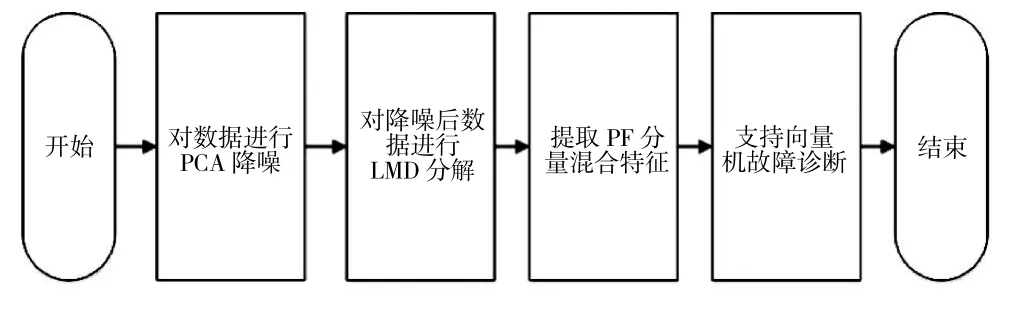
图1 轴承故障诊断方法流程

首先，对轴承振动信号进行PCA 降噪；其次，对降噪后的轴承振动信号进行LMD 分解；再次，提取分解得到的PF 分量混合特征以表征轴承的运行情况；最后，将提取到的混合特征输入到支持向量机多分类器进行诊断。

1.1 PCA 降噪

近年来，PCA 降噪的主要思路为：对单一信号进行相空间重构，将信号扩展为多维，而后进行主成分分解与重构，PCA 降噪的具体方法见文献[11]。

1.2 局部均值分解

LMD 局部均值分解是1 种自适应时频分析方法，对于1 个信号，局部均值分解可以将其分解为一系列PF 分量，每阶PF 分量都是由1 个包络信号和1个纯调频信号相乘得到的单分量调幅-调频信号，其具体的步骤见文献[16]。对1 个降噪后的轴承振动信号XR(nt)的分解结果为

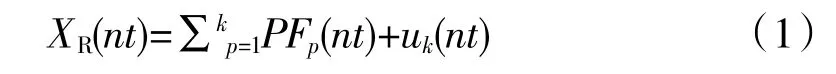
式中：PFp为LMD 分解得到的第p 阶PF 分量；uk为LMD 分解完成后的残余分量。

局部均值分解可采用滑动平均法[17]对局部均值函数和局部包络函数[18]进行平滑处理。滑动平均法的步长对于分解结果的好坏有很大影响，轴承振动信号的非平稳特性使得滑动平均法分解结果并不理想；通过样条插值代替滑动平均求取局部均值和局部包络函数，则可以在一定程度上提高分解效果。故本文采用3 次样条插值代替滑动平均法求取局部均值函数和局部包络函数。

1.3 PF 分量特征提取

提取了降噪后信号XR经LMD 分解所得PF 分量的能量比特征、样本熵特征、均方根特征、均值特征、歪度特征、峭度指标特征、波形指标特征、脉冲指标特征及裕度指标特征共9 类特征。通过使用单一特征进行故障诊断与分类，得到一系列故障诊断结果。根据诊断结果最终选取对于不同故障数据可分性较好的能量比特征、样本熵特征、均方根值特征、峭度指标特征及波形指标特征作进一步分析与选取。

1.3.1 能量比特征

对于降噪后的轴承振动信号XR，LMD 可以将其分解为多阶PF 分量，各阶PF 分量的能量与总能量的比值为能量比特征，反映了各阶分量在能量上的混乱程度。其第k 阶PF 分量能量比特征为

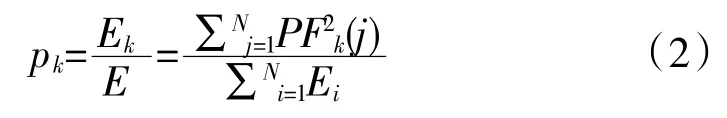
式中：PFk为第k 阶PF 序列第j 个元素值；Ei为第i阶PF 分量所包含的能量；E 为各阶PF 分量的总能量；pk为第k 阶PF 分量的能量占比。

1.3.2 样本熵

样本熵可以反映时间序列的复杂程度，对于第k阶PF 分量[PFk(1),PFk(2),PFk(3)…PFk(N)]，其样本熵计算步骤如下。

给定维数m，根据原始序列形成矢量M（i）

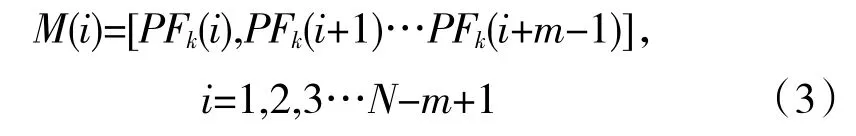
定义矢量M(i)与M(j)之间的距离为

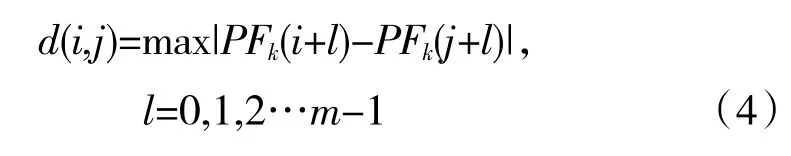
设定相似容限参数r，对于每个给定的M(i)，统计其小于r 的d(i,j)的点位数Ki及其与样本总数N-m+1的比值，记作

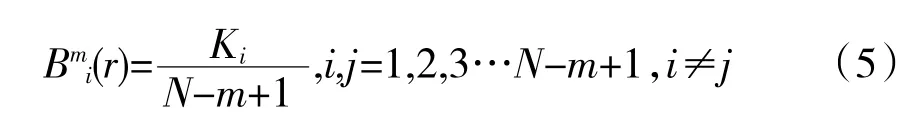
求取Bmi(r)的平均值得

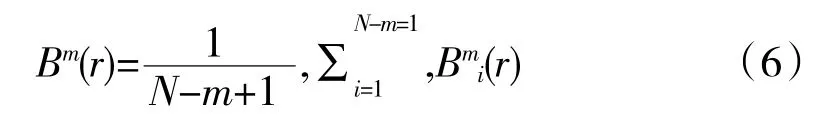
令m+1，重复步骤（3）～（6），得到Bm+1(r)；由此，可得此PF 分量序列的样本熵为

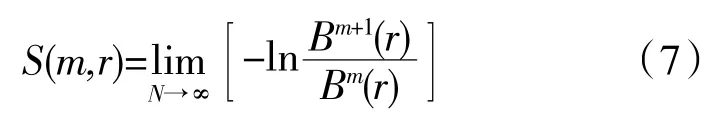
若N 为有限值，那么长度为N 的序列的样本熵的估计值为

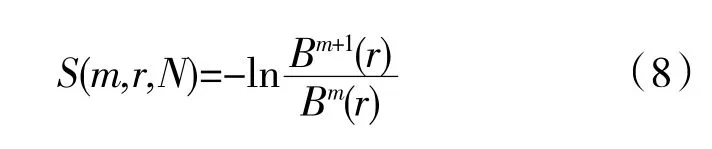
本文设置样本熵模式维数为2，对其相似容限参数设置为0.25stdk，stdk为选取序列的标准差。

1.3.3 均方根值

均方根值是1 种传统的有量纲时域特征，对长度为N 的第k 阶PF 分量序列，均方根值特征定义为

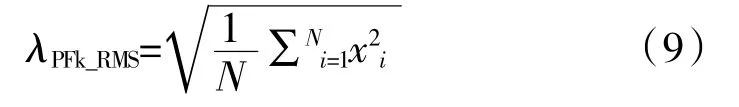
1.3.4 峭度指标

峭度指标特征是1 种传统的无量纲时域特征，反映了轴承的冲击成分，对于长度为N 的第k 阶PF 分量序列，其峭度指标特征定义为

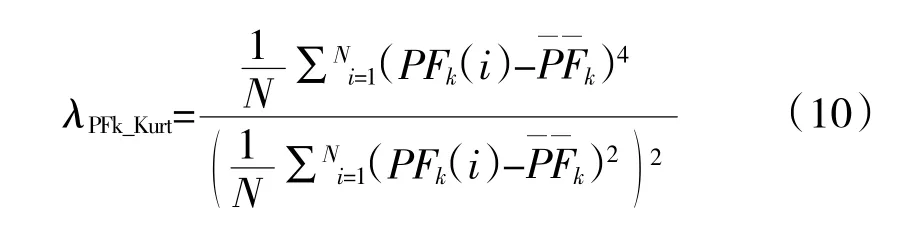
1.3.5 波形指标

波形指标是1 种传统的无量纲时域特征，对长度为N 的第k 阶PF 分量序列，其波形指标特征定义为

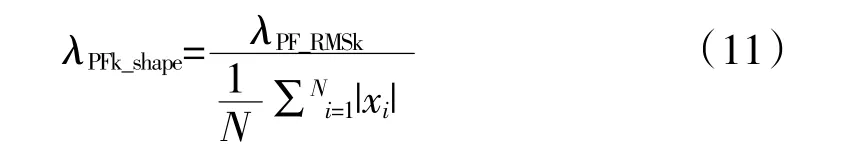
1.4 支持向量机

支持向量机是1 种二分类器，是1 种机器学习方法，在处理小规模数据分类方面，其效果优于神经网络等分类器，支持向量机的主要步骤见文献[18]。由于支持向量机只能处理二分类问题，而轴承的故障诊断是多目标分类问题，必须对支持向量机使用方法做出改变，才可适用。传统的支持向量机多目标分类器有1对1 和1 对多2 种形式，本文采用1 对1 的形式构建支持向量机多目标分类器，用于滚动轴承的故障诊断。

2 试验分析

试验数据来源于美国凯斯西储大学实验室的轴承故障数据库[19]，试验用轴承为SKF6205RS 深沟球轴承，轴承的内、外径和宽度分别为25、52、15 mm，钢球直径为7.94 mm，节圆直径为39.04 mm。轴承位于电机驱动端，采用加速度传感器采集信号，采样频率为12 kHz，使用电火花切割轴承内、外圈，滚动体制造单点损伤，电机转速为1797、1772、1750 及1730 r/min，损伤点直径分别为0.1778、0.3556 和0.5334 mm，其不同损伤点直径对应的故障信号分别定义为轻微、中度和严重故障信号。使用每组信号前40960个点位的数据进行截断，截断成10 组，每组长4096个点位，共400 组，由于转速为1750 r/min、中度故障的滚动体故障信号缺失，使用转速为1772 r/min、中度故障的滚动体故障信号后40960 个点位代替。

2.1 PCA 降噪

以轴承转速为1772 r/min、轻微内圈故障信号为例，验证PCA 降噪的效果。内圈故障的时、频域信息如图2 所示。从图中可见，信号存在明显的噪声，据文献[13]，噪声会使轴承振动特征频率产生偏移，增加故障特征提取的难度。因此，需要对原始信号进行预处理。

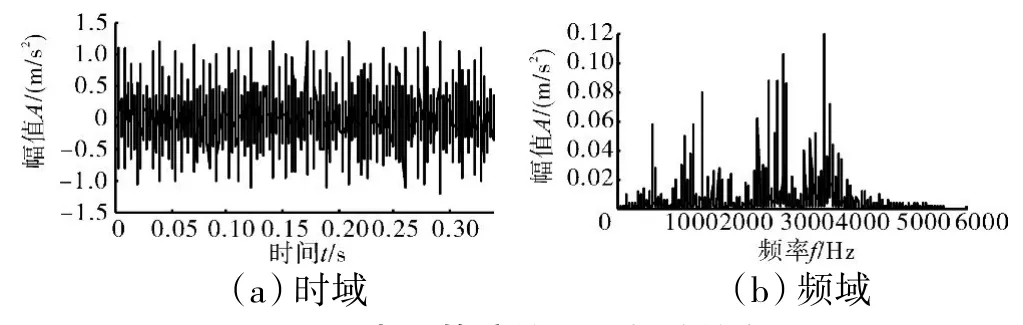
图2 内圈故障信号时频域信息

选取Hankel 矩阵的行数m=2048，列数n=2049，则Hankel 矩阵的主成分数为2049，可用特征值数为2048，对根据内圈故障数据构建的Hankel 矩阵进行主成分分解，得到其特征值λ 和累计方差贡献率如图3 所示，累计方差贡献率及特征值见表1。从图中可见，对于分解得到特征值，其主要特征值集中在前500 个，对应的累计方差贡献率为0.9543，而后方1548 主成分的贡献率仅为0.0457。从表中可见，随着特征值数的增大，每提升0.05 的累计方差贡献率所需的特征值数也在不断增加，从0.90 增大到0.95 需要164 个特征值，而从0.95 增大到0.99，则需要435 个特征值。

可见，后方较小的特征值及其所对应的主成分对数据的贡献率较小，且随着特征值数的增加，其对数据的贡献率在不断减小，因此，选取贡献率为0.90 为判据进行降噪，结果如图4、5 所示。

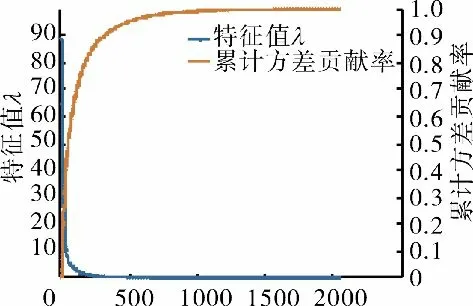
图3 特征值λ 及其累计方差贡献率

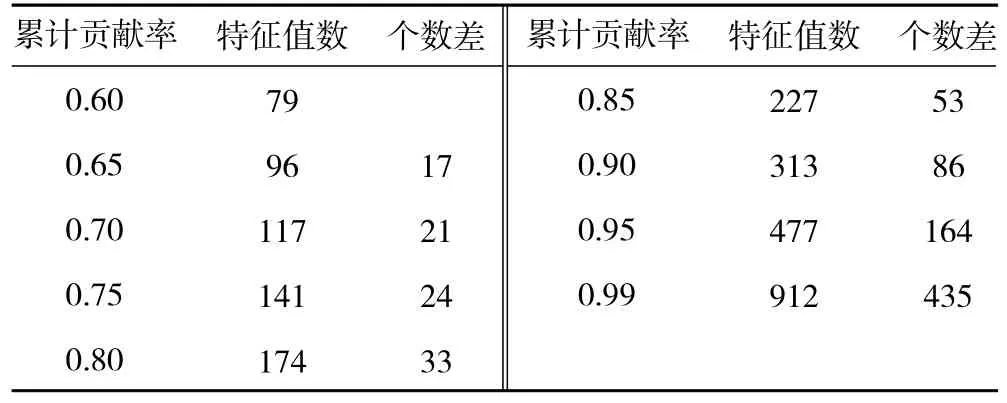
表1 累计方差贡献率及特征值

从图4、5 中可见，降噪后信号的域波形没有发生太大变化，而其频谱的毛刺被去除很多，变得更加光滑，且突出了故障特征频率。据此，在PCA 降噪的基础上进行特征提取是有效的。

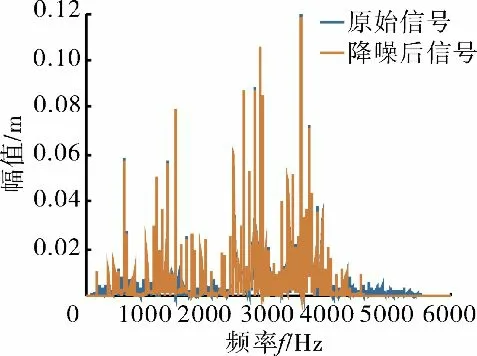
图4 降噪信号与原始信号频域图像

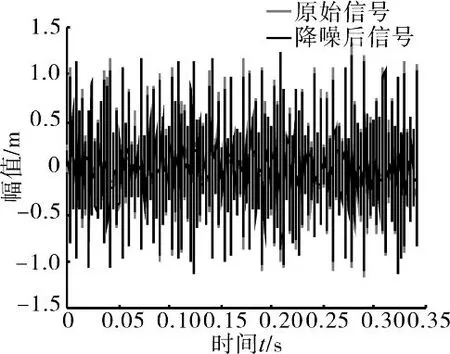
图5 降噪信号与原始信号时域图像

2.2 混合特征提取

对降噪后的内圈故障信号进行LMD 分解，得到的结果如图6、7 所示。从图6 中可见，LMD 将信号自适应分解成6 个PF 分量；从图7 中可见，6 个分量所处频段大小依次降低，同时，发现其主要的频率信息集中在前5 阶PF 分量中，故本文选取前5 阶PF 分量作为分析用PF 分量。

图6 信号LMD 分解时域信息

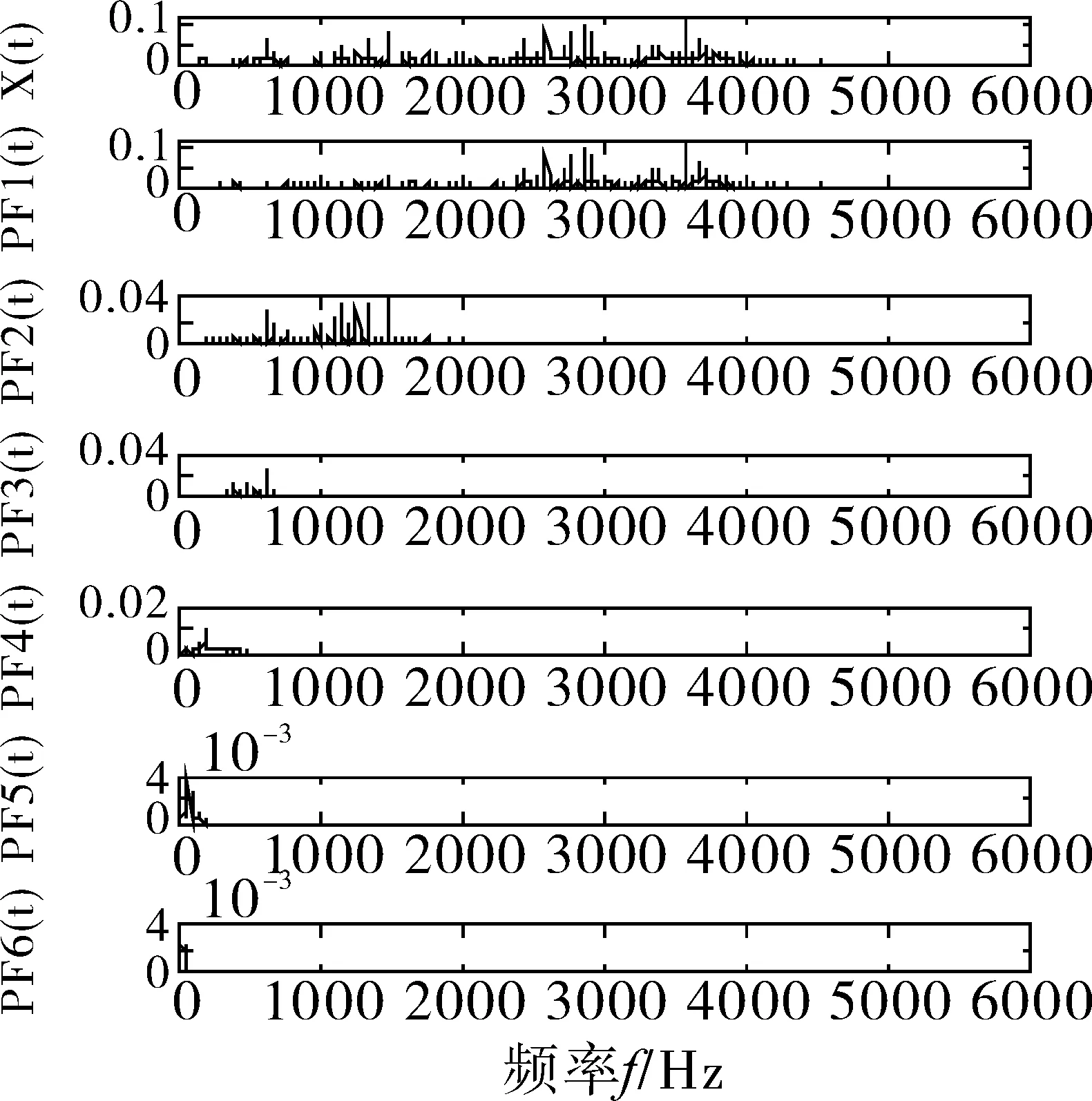
图7 信号LMD 分解频域信息

2.2.1 能量比特征

现以在1730 r/min 转速下，3 种故障深度的滚动体、内圈与外圈故障为例，进行故障特征的研究与选取，每种深度的故障信号8 组，所得的结果如图8、9 所示。

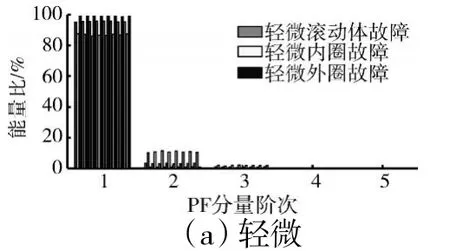
图8 不同故障不同程度的信号PF 分量能量比值特征

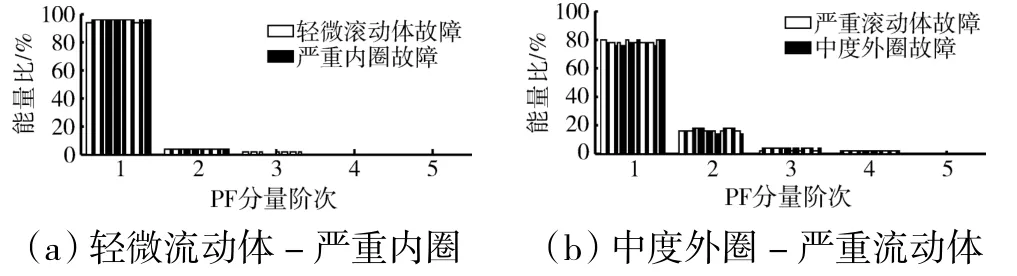
图9 故障深度变化引起的PF 分量能量比特征重叠

从图8 中可见，在单一故障深度下，PF 分量能量比特征可以区分轻微故障信号和中度故障信号。对于轻微故障，可分性较好的特征为前2 阶；对于中度故障，可分性较好的特征为第2、3 阶；对于严重故障，其对内外圈故障信号的可分性不大，但可区分滚动体故障与其余2 类故障。由故障深度的变化，轻微滚动体故障信号和严重内圈故障信号PF 分量能量比特征产生一定的重叠，严重滚动体故障信号和中度外圈故障信号的PF 分量能量比特征也产生一定的重叠（图9）。综上，采用能量比特征作为混合特征之一，但由于能量比特征产生了多处重叠，需要其他特征来补充能量比特征的不足。

2.2.2 峭度特征

进一步对比不同故障、不同深度的故障信号PF 分量的峭度指标特征，如图10、11 所示。

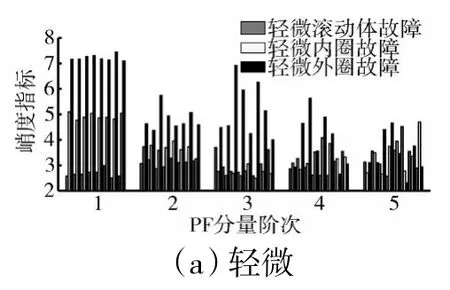
图10 不同故障不同程度的信号PF 分量峭度指标特征

从图10 中可见，在同一故障深度下，PF 分量峭度指标特征可以在一定程度上区分3 种故障信号，故可以对PF 分量能量比特征起到一定的补充作用。但是，PF 分量峭度指标特征稳定性较差；对于轻微故障，外圈故障信号后4 阶特征稳定性较差，内圈与滚动体故障信号后3 阶特征稳定性也较差；对于中度故障，滚动体信号和内圈信号的第1 阶特征稳定性不好；对于严重故障，外圈故障信号的PF 分量峭度指标特征稳定性不好。

从图11 中可见，由于故障深度的变化以及受PF分量峭度指标特征本身稳定性的影响，轻微滚动体故障信号和中度外圈故障信号的PF 分量峭度指标特征产生了一定重叠。

虽然PF 分量峭度指标特征对于故障信号有一定的可分性，且可以对能量比特征起到一定的补充作用，但其稳定性不好，本文最终未选取PF 分量峭度指标特征作为故障诊断用特征。

各所属公司也积极利用国家加大对水务、环保投入的有利大环境，努力争取国家和当地政府的政策性支持，开源节流，降本增效，推行精细化管理，为公司运营营造了良好的内外部环境。

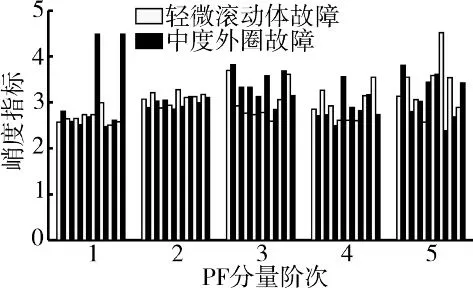
图11 故障深度变化引起的PF 分量峭度指标特征重叠

2.2.3 波形指标

同样，对比不同故障、深度的故障信号PF 分量的波形指标特征如图12、13 所示。

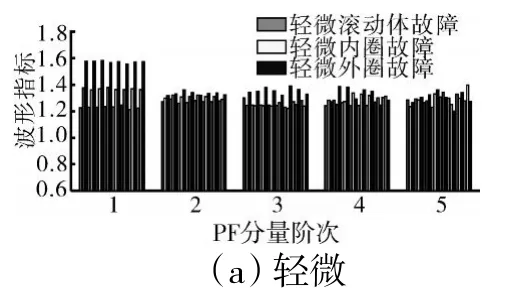
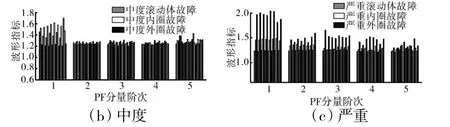
图12 不同故障不同程度的信号PF 分量波形指标特征

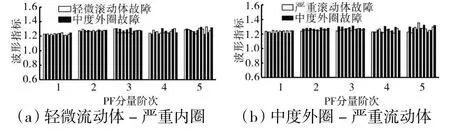
图13 故障深度变化引起的PF 分量峭度指标特征重叠

从图13 中可见，随着故障深度的变化，轻微与严重滚动体故障信号同中度外圈故障信号的PF 分量波形指标特征产生一定的重叠，但轻微滚动体故障信号和严重内圈故障信号的PF 分量波形指标特征并未因故障深度的变化而产生重叠，可以对PF 分量能量比特征起一定的补充作用。

PF 分量波形指标特征对故障信号有一定的可分性，且可以对PF 分量能量比特征起一定的补充作用，本文采用PF 分量波形指标特征作为混合指标的1 种，但仍需要其他特征来补充其不足。

2.2.4 样本熵特征

对比不同故障、深度的故障信号PF 分量的样本熵特征，如图14、15 所示。

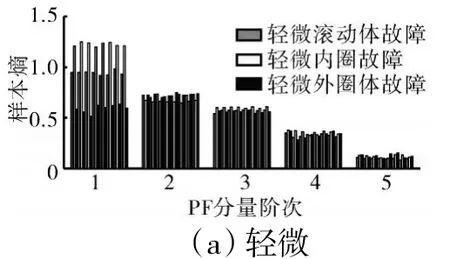
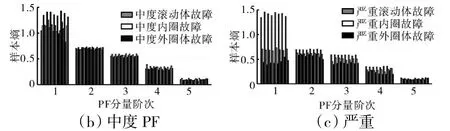
图14 不同故障不同程度的信号PF 分量样本熵特征

从图14 中可见，在同一故障深度下，PF 分量样本熵特征可以区分轻微故障信号和严重故障信号。对于轻微故障，前3 阶PF 分量样本熵可以在一定程度上区分3 种故障信号；对于严重故障，前4 阶PF 分量样本熵特征有一定的可分性；对于中度故障，由于滚动体故障信号第1 阶PF 分量样本熵稳定性不好，滚动体与内圈故障信号的PF 分量样本熵特征会产生一定重叠。

本文选用PF 分量样本熵特征作为混合特征的1种，但需要其他特征补充PF 分量样本熵特征的不足。

2.2.5 均方根值特征

最后，对比不同故障、深度的故障信号PF 分量的均方根值特征，如图16、17 所示。

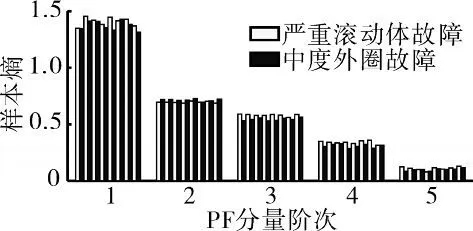
图15 故障深度变化引起的PF 分量样本熵特征重叠

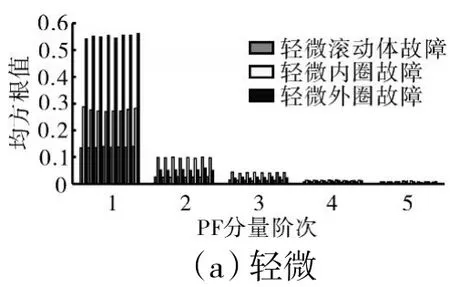
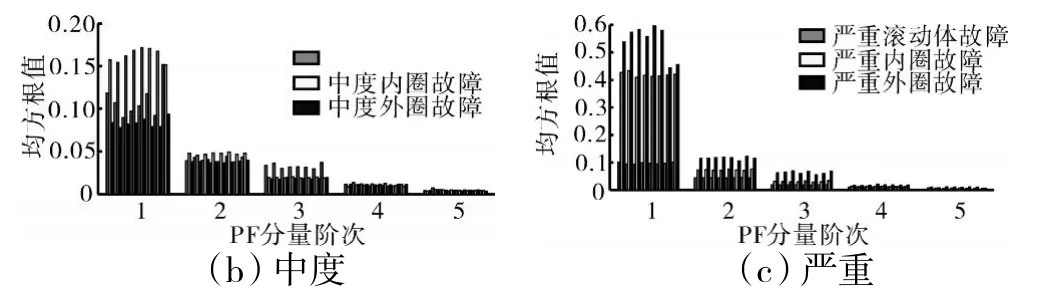
图16 不同故障不同程度的信号PF 分量均方根值特征

从图16 中可见，在同一故障深度下，PF 分量均方根值特征可以有效地区分故障信号，可分性较好的特征为前3 阶PF 分量均方根值特征。通过对比，发现故障深度的变化并未使PF 分量均方根值产生太大的重叠。从图17 中可见，严重滚动体故障信号和中度外圈故障信号的PF分量均方根值特征并未产生重叠，故可以对前面所选取的特征起到很好的补充作用。

由PF 分量均方根值特征可以有效地区分故障信号，且可以对前面所选特征起到补充作用，本文选取PF 分量均方根值作为混合特征之一。

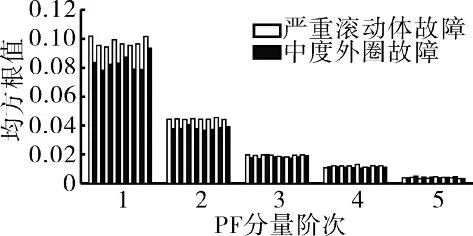
图17 严重滚动体故障与中度外圈故障的信号PF 分量均方根值特征

2.3 SVM 故障诊断的验证

采用1 对1 的形式构建支持向量机多目标分类器进行故障诊断，考虑到转速对故障诊断的影响，使用各种转速下故障与正常信号前5 组特征作为训练集，其余特征作为检验集，共有训练集200 组，检验集200 组，具体的数据见表2。

为验证本文方法的有效性，采用本文特征（特征a）进行SVM 故障诊断，得到的结果见表3。

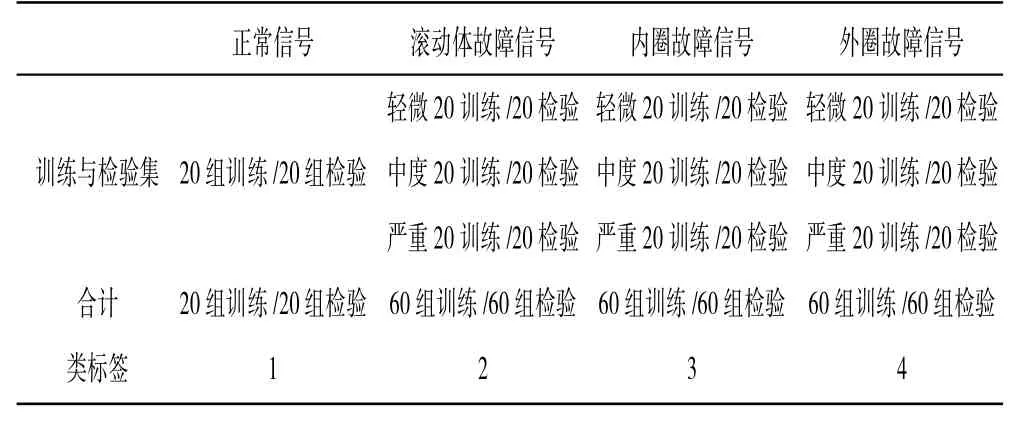
表2 故障信号数据

表3 故障诊断结果1

从表中可见，故障诊断结果在中度滚动体故障处出现4 个错误，故障诊断正确率为98%。

为检验考虑PF 分量峭度指标混合特征的诊断效果，使用特征b，用峭度指标代替波形指标和特征c，同时引入峭度指标和波形指标进行对比验证，得到的结果见表4。

表4 故障诊断结果2

从表中可见，对于特征b，将PF 分量峭度指标特征替换掉PF 分量波形指标特征后，滚动体故障、内圈故障和外圈故障均出现了误诊，诊断率降为95%；相较于特征a，分类效果变差。对于特征c，在本文所选特征的基础上加入PF 分量峭度指标，对中度和严重内圈故障诊断各出现1 个错误，故障诊断率略有降低。

进一步采用本文所使用特征与文献[13]使用的特征d、文献[14]使用的特征e，进行故障分类对比；在本文所选取的分类条件下，所得结果见表5。

表5 故障诊断结果3

从表中可见，对于特征d，经过SVM 故障诊断后，在中度和严重滚动体故障处各出现5 个和1 个错误，在中度和严重内圈故障处各出现14 个和2 个错误，在轻微外圈故障处出现13 个错误，错误主要集中在内圈与外圈故障处；对于特征e，发现其诊断结果在中度和轻微滚动体故障处各出现2 个和1 个错误，在轻微内圈故障处出现7 个错误，在中度和严重外圈故障处各出现3 个和1 个错误，主要在内圈故障处出现一些错误。2 种方法的正确诊断率与本文方法对比明显降低。

3 结束语

提出1 种基于PCA-LMD 混合特征的故障特征提取方法，用PCA 对轴承振动信号去噪，采用PF 分量样本熵、能量特征、均方根值和波形指标所构成的混合特征进行支持向量机故障诊断，可以同时综合识别轴承的不同故障类型、不同深度的故障，提高故障诊断率。本方法可推广应用于航空发动机轴承的故障诊断。在实际工程中常常存在同一特征对应多种不同故障，同一故障又有多个特征的现象，给轴承的故障诊断带来困难，使得利用混合特征进行诊断尤为重要。如何融合各信号特征，特别是多种故障和多种故障程度同时存在时的正确诊断，还有待于进一步深入研究。