煤层开采对地表变形影响的数值模拟研究

孙 超，魏发达，冯智慧

吉林建筑大学 测绘与勘查工程学院,长春 130118

我国领土幅员辽阔,具有丰富的煤矿资源,随着我国经济的增长和开采工艺的成熟,对于地下埋深较大的煤层开采和使用已有成熟的开采方法[1],特别是“三下压煤”开采使得我国采煤利用率大幅提高[2].在开采“三下压煤”时对地上建筑物或构筑物的沉降和水平位移等指标有严格的控制[3],因此，在煤层开采前有必要对其开采后采空区的顶部沉降和对地上建筑物或构筑物位移影响进行计算.随着计算机数值模拟技术不断成熟，通过数值模拟可以直观的看到开采后的沉降及应力的变化,并在投入成本较小的情况下对方案进行调整,为地面建筑物提供安全性保证[4-5].本文采用FLAC3D数值模拟软件[6-7],选取摩尔-库伦、弹性及德鲁克-普拉格3种常用的岩土体本构模型,分别模拟煤层开采对地表建筑物竖直沉降和水平位移的影响,并与概率积分理论计算[8]结果进行对比分析，以期为地表竖直和水平位移的设计控制及合理选择数值模拟本构模型提供理论依据.

1 工程概况

该模拟工程属于“三下压煤”工程中的建筑物下压煤,煤矿开采标高为-225 m，开采厚度为5 m,开采宽度为200 m,地上建筑物为18层住宅楼，距离煤矿开采边缘20 m.该工程共分为六层地质层.第一层为粉质粘土层,厚度为20 m;第二层为砂泥岩交互层,厚度为50 m;第三层为泥质砂岩层,厚度为60 m;第四层为粉砂岩层,厚度为70 m,第五层为煤层,厚度为50 m;第六层为砂岩层,厚度为70 m,地层及尺寸如图1所示.

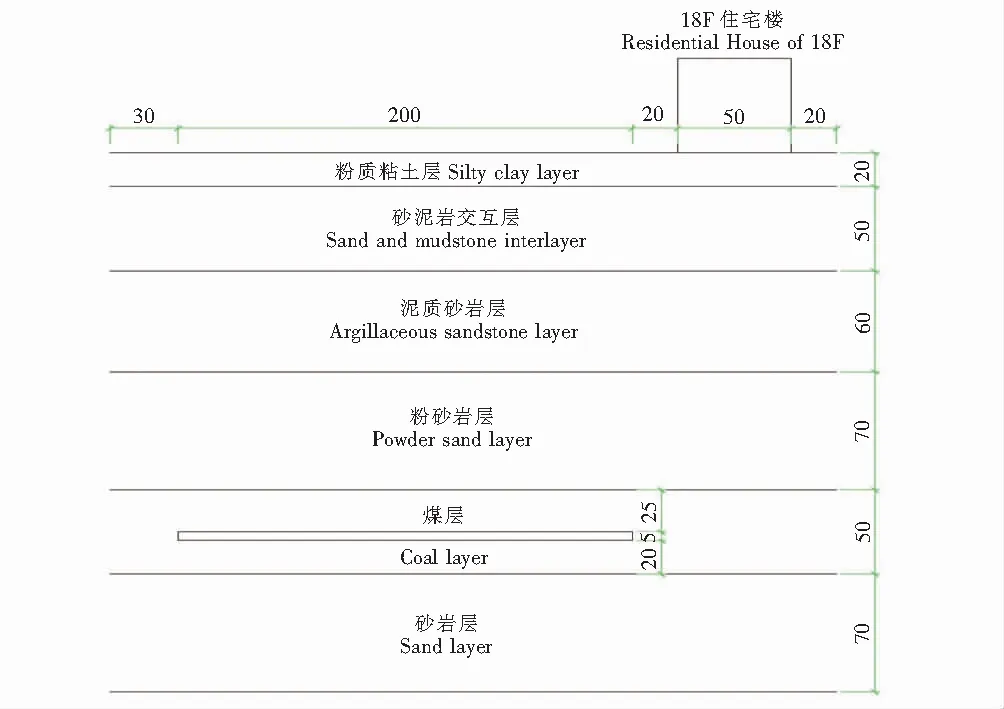
图1 地层及尺寸

2 概率积分法理论计算

概率积分法是应用最广泛的预算方法之一，因其所用的移动和变形预算公式中含有概率积分(或其导数)而得名.通过对单元开采进行积分可以得出开采工作面对地表任一点的移动与变形计算公式,即：

(1)

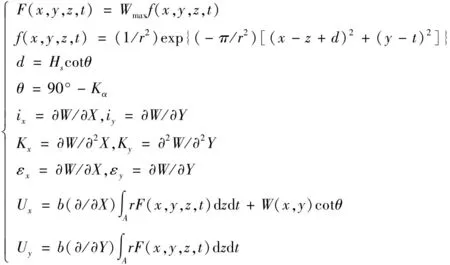
式中,ψ为x轴与j方向的夹角,°;Wmax为最大沉降值,mm;α为煤层倾角,°;A为有效开采面积,m2;r为有效影响半径,m;b为水平移动系数;θ为影响传播角度,°;K为影响传播系数;Hs为开采深度,m;x,y为假定坐标系中的坐标,m;z,t分别是沿上山方向和走向方向的积分变量,m.

3 FLAC3D数值模拟

3.1 模型建立

为了保证数值模拟的准确度和模型的计算速度,本次模拟选取的是标准段位置的截面,取模型尺寸为320 m×320 m×1 m,具体尺寸如图1所示.网格尺寸取为1 m×1 m×1 m,模型网格如图2所示.模拟采用的是留设煤柱的方式进行开采,取煤柱宽度为7 m，煤柱间距为20 m.为了监测开采后地表沉降对地表建筑物住宅楼的影响程度沿A点至B点每隔10 m设置一个监测点，共设置6个监测点用来监测地表住宅楼的竖直沉降位移和水平位移,并且在采空区顶部设置监测点用来观察采区顶部沉降情况.

图2 模型网格

3.2 参数选取

本模型地质层共分为六层,土层及及寸信息见图1，土层参数如表1所示[9].

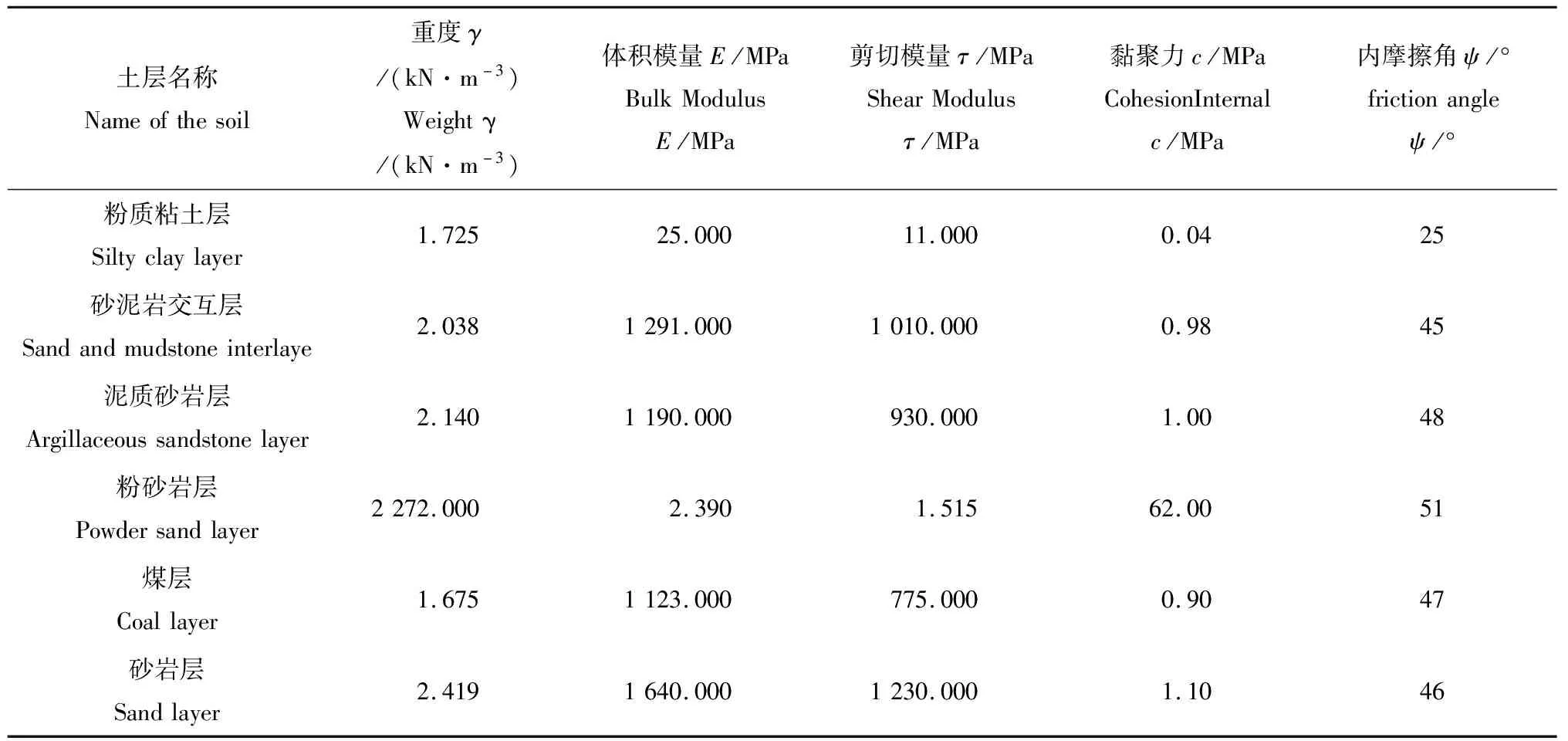
表1 土层参数

3.3 模拟结果及分析

通过3种本构模型分别进行FLAC3D数值模拟初始地应力平衡云图,如图3所示.

图3 摩尔-库伦本构模型,弹性本构模型,德鲁克-普拉格本构模型初始地应力平衡云图

由图3可以直观的看出,摩尔-库伦,弹性及德鲁克-普拉格3种本构模型计算得出的最大初始地应力分别为7.07 MPa,7.08 MPa,7.90 MPa.

4 理论与模拟计算结果对比分析

通过FLAC 3 D数值模拟计算及概率积分法计算建筑物的竖直位移曲线如图4 所示,水平位移曲线如图5所示.

图4 建筑物竖直位移曲线图

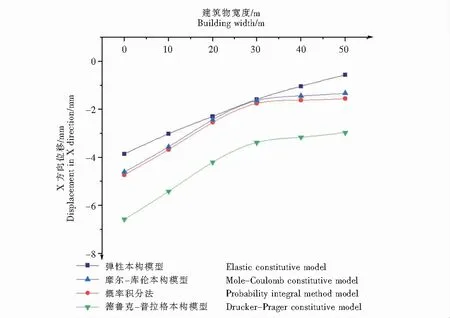
图5 建筑物水平位移曲线图

由图4、图5看出,相对于4种计算结果,弹性本构模型模拟所得结果相对较小,最大沉降为49.3 mm,沉降差为4.1 mm,最大水平位移为4.6 mm,水平位移差为3.3 mm；德鲁克-普拉格模拟所得相对较大,最大沉降为65.3 mm,沉降差为7.2 mm,最大水平位移为6.5 mm,水平位移差为3.3 mm；摩尔-库伦本构模型所得结果中,最大沉降为52.7 mm,沉降差为4.7 mm,最大水平位移为4.6 mm,水平位移差为3.3 mm；概率积分理论计算法中,最大沉降为52.6 mm,沉降差为4.7 mm,最大水平位移为4.7 mm,水平位移差为3.2 mm.

由此可见,摩尔库伦与概率积分理论计算结果较为接近，且符合规范开采要求[10],故更适合煤层开采对地表建筑物影响的数值模拟研究.

同时,由图4、图5可以看出,竖直和水平位移均为靠近开采处逐渐增大,远离开采处逐渐减小并趋于稳定.

5 结论

通过3种本构模型下FLAC3D数值模拟计算结果与概率积分法理论计算结果的对比分析,可得以下结论：

(1)数值模拟计算与理论计算均可得出竖直和水平位移均为靠近开采处逐渐增大,远离开采处逐渐减小并趋于稳定.

(2)相对于4种计算结果,弹性本构模型模拟所得结果相对较小,而德鲁克-普拉格本构模型模拟所得结果相对较大,可见弹性本构模型适用于应力-应变呈线性关系各向同性连续介质材料中,德鲁克-普拉格本构模型更加适合适用软粘土的地质情况中.

(3)摩尔-库伦本构模型更适合煤层开采对地表建筑物影响的数值模拟研究.