一种基于温度动态估计的AUV 锋面跟踪算法
曲向宇 ,李一平
(1. 中国科学院沈阳自动化研究所 机器人学国家重点实验室,辽宁 沈阳 110016;2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;3. 中国科学院大学,北京 100049)
海洋锋面是指海洋中存在两种或多种理化性质显著不同的水体的区域,该区域水文要素呈现较高的水平梯度,在空间上呈狭长带状结构[1]。因为锋面区域内的能量交换非常强烈,所以海洋锋面在海洋动力学的研究中十分重要。同时,由于锋区内存在特殊的物理过程,特别是上升流现象,使得该区域海水富营养化,海水初级生产力提高,与海洋产业活动联系十分紧密。另外,海洋锋面对水声通信技术的影响也非常明显。因此,研究和观测海洋锋面这种海洋现象,对于海洋科学、海洋渔业以及海洋军事作战具有重大意义[2]。
常规的海洋特征观测方法如潜标、浮标,使用相应的传感器,在固定的位置或在漂流状态下进行观测。而自主水下机器人(AUV)利用自身搭载的传感器,可以实现对目标区域水文要素的连续动态观测,相较于常规方法具有快速性和自主性的优点[3]。由于锋面这种海洋特征,易受风、海流等因素影响,水文要素复杂且变化较快,为了快速对指定区域采样,通常使用AUV 进行海洋特征的观测[4]。
AUV 通常采用梳状观测方法,对感兴趣区域进行覆盖观测,但该方法缺乏自主性和灵活性,不适合作为海洋特征观测的方法[5-6]。Zhang Y 等[7-8]提出了一种基于温度梯度阈值的“之”字锋面跟踪算法,该方法设置了锋面的温度梯度阈值,用来判断AUV是否进入锋面,并通过对航向角的调整,实现AUV在观测区域内的往复锋面跟踪。Wang D[9]根据实时观测到的温度数据,利用最小二乘法估计锋面区域的梯度方向,保持AUV 沿着温度梯度上升或下降的方向前进,当到达设定的等温线进行折返,实现AUV 在指定温度边界之间的锋面跟踪。考虑到锋区的形态往往较为复杂,需要锋面跟踪算法具有较高的环境适应性,避免陷入特定区域重复观测。基于以上考虑,本文提出了一种基于温度动态估计的锋面跟踪算法,在AUV 到达锋面边界时,通过沿等温线跟踪一段距离,来加快锋面跟踪速度,并脱离“陷阱”区域,保持了对锋面的持续跟踪能力;选用高斯过程回归(GPR),替代最小二乘法作为温度动态估计的方法,增加了近邻区温度预测的准确性[10-12]。
1 锋面区域模拟
1.1 研究区域
中国的东部近海在冬季有着稳定丰富的海洋锋面现象。本文选取一个典型的沿岸锋面——山东半岛南部“N”形锋面作为研究对象。该锋面在冬季位置稳定,具有规则的形态,在121°E 西面平行于海岸线,在 121°E,36°N(A 区域)以东呈离岸走势,向东南方向约伸展到 122°E,35.5°N 附近,在该位置东面,沿东北方向分布至山东外海。该锋面呈现了一个完整的“N”形结构,在12 月中旬至2 月中旬之间,锋面丰富且形态成熟,3 月份之后逐渐消亡[13]。考虑到AUV 的续航力有限,无法对整个锋面全部观测,故本文选取“N”形锋面的A 区域,用于锋面跟踪算法的仿真验证。
1.2 温度数据获取与处理
本文选用MODIS 海温卫星遥感资料作为锋区温度数据来源,MODIS 的L3 级数据产品可提供全球范围的遥感数据。文中所需的海水表层温度(SST)数据由美国国家航空航天局(NASA)网站免费提供,下载的数据集名称为AQUA_MODIS.20191211.L3m.DAY.SST.sst.4 km.NRT.nc,空间分辨率为4.64 km,时间分辨率为1 d。通过对数据集的处理,可以绘制出“N”形锋面的SST 图像。如图1 所示,给出了在2019 年12 月11 日该区域的海水温度情况。

图1 山东半岛南部“N”形锋面
从图中可以明显地观察到“N”形锋面的形态和位置,其中锋面的 A 区域在 121°E、36°N 附近。进一步缩小数据集范围,A 区域SST 图像如图2 所示。
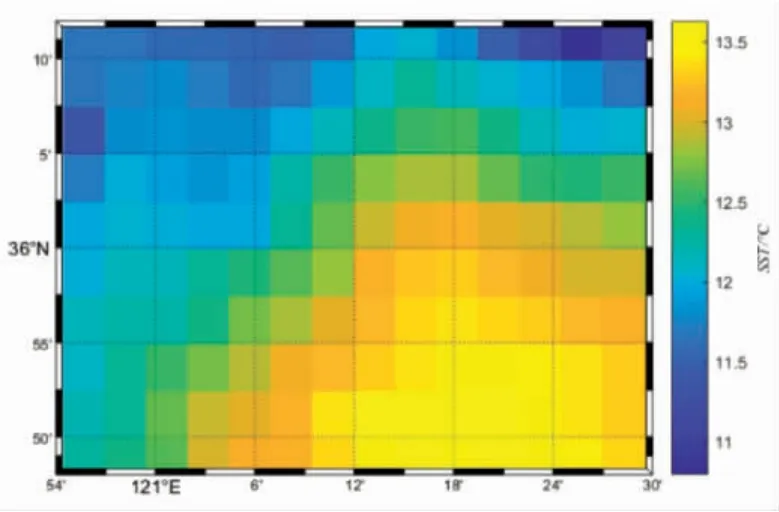
图2 锋面A 区域
考虑数据集中温度值的空间分辨率为4.64 km,图2 中所示区域内的数据点过少,无法满足在锋面跟踪任务中对算法对采样数据的处理需求。因此,本文利用样条函数插值的方法对所选区域的数据点进行插值处理。定义了一个长度为45 km、宽度为35 km 的任务区域,设置温度数据点的间距为0.1 km,经插值后得到的A 区域温度场如图3 所示。至此,本文完成了任务所选锋面区域的温度场模拟。

图3 插值后的锋面A 区域
2 锋面跟踪算法
考虑到海洋特征的水平与垂直性质,AUV 通常采用水平分层观测或者垂直剖面观测的方法进行特征跟踪。由于锋面具有较高的温度水平梯度,一般令AUV 在固定的深度执行锋面观测任务。本文利用AUV 近一段时间内采集的温度数据,通过高斯过程回归的方法预测近邻区温度分布,并根据预测结果,选取AUV 下一次锋面跟踪的路径点。在路径规划阶段,首先判断AUV 所处锋区位置,若在锋区内部,则保持跟踪路径沿着温度梯度方向,在锋区内执行梯度下降或上升的锋面跟踪动作;当航行到锋面边界时,采取沿等温线跟踪的动作。本文提出的锋面跟踪算法流程图如图4 所示。
2.1 预规划
本文令AUV 在观测区内的等温线Thot和Tcold之间(冷热水团分界面),进行锋面跟踪任务。当开始执行任务时,假定AUV 的任务初始点在任务区域外,令其沿着预定义航向运动到等温线Thot或Tcold上,之后开始执行锋面跟踪算法。这样做有两个好处,一是AUV 的布放位置可以有更多的选择,二是为温度预测累计输入样本。
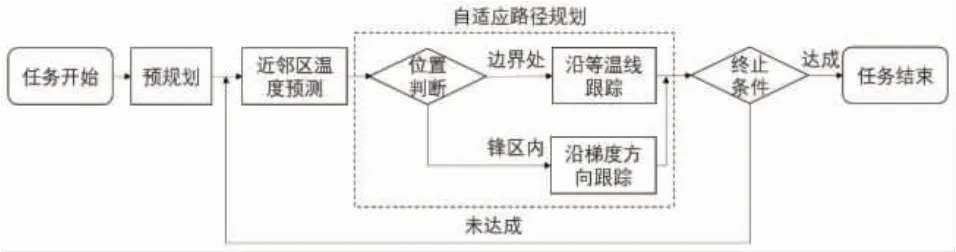
图4 本文锋面跟踪算法流程图
2.2 近邻区温度预测
高斯过程回归(GPR)是一种优秀的环境模型估计方法,本文利用GPR 方法对AUV 一段时间内采样的温度数据进行分析,来预测当前位置附近区域的温度场分布。已知AUV 在锋区近一段时间内n次温度采样的数据,其中输入位置集合X={xi∈Rd|i=1,2,…,n},对应有温度集合 y={yi|i=1,2,…,n},共同构成训练数据集D={X,y}。利用GPR 方法,可对D 找到反映出训练集合内输入与输出之间的函数映射关系,并根据测试位置X*,求出对应的预测值y*,获得了指定位置的温度预测值。
在任务区域内,AUV 保持固定航速,Δt 为相邻采样时间间隔,相邻采样点之间的距离为R0。随着任务执行时间的不断增加,AUV 温度采样的数据越来越多。若将所有的数据都作为GPR 的样本输入,无疑会增加温度预测的数据处理时间,并且较早的历史数据会干扰当前位置的预测结果。本文通过设定预测窗口宽度m,来定期更新GPR 的样本输入数据集合。如果采样点无法填满窗口,将宽度m 临时调整为此时的采样点数量。
2.3 自适应路径规划
AUV 的自适应路径规划主要被分为两种情况,沿梯度方向跟踪和沿等温线跟踪。通过判断AUV当前位置,决定其下一步规划执行的具体任务。如图5 所示,为自适应路径规划的示意图。
2.3.1 位置判断方法 本文将温度阈值作为对AUV 位置进行判断的条件,表示为:
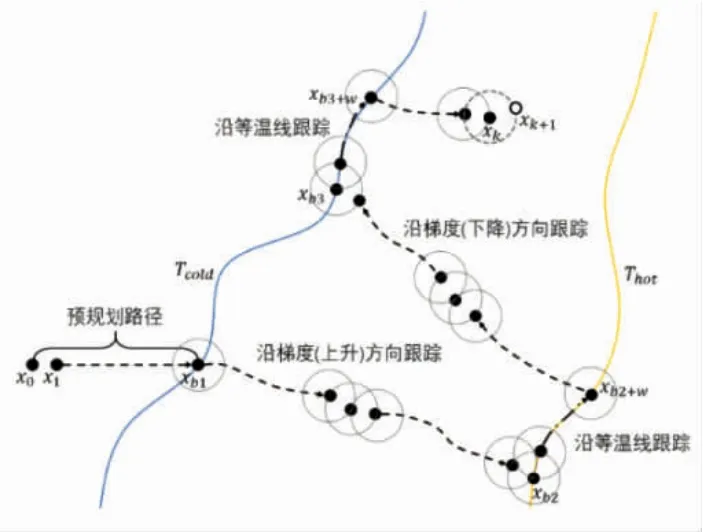
图5 自适应路径规划示意图

式中:Tk表示当前位置的温度值;Tb为上一次所达边界的温度值;阈值当满足ΔT≥Tth时,判断当前位置位于等温线边界,开始执行沿等温线跟踪任务,并且令Tb=Tk,更新边界温度;若不满足,判断位于锋区,继续执行沿梯度方向跟踪任务。
2.3.2 沿梯度方向跟踪 锋区具有较高的温度水平梯度,本文定义从温度边界Thot向Tcold运动时,执行梯度下降搜索策略,反之执行梯度上升搜索策略。海洋锋面是动态变化的,为了提高观测速度,结合实时预测的温度场可以确定锋区内AUV 相邻观测点之间的最优距离R。考虑预测温度场的准确性随距离成负相关,观测点之间的距离不宜过大,定义Ri∈[R0hR0],其中h 为常数。若AUV 当前位置为xk,温度值为yk,利用GPR 对与当前位置距离为Ri的圆形观测区域的温度场进行估计,可以获得温度预测集合YRi,对应位置坐标集合PRi。若为梯度上升方向,对应Ri的估计梯度值GRi表示为:

若为梯度下降方向,GRi表示为:

式中:αRi为距离权重因子,衡量预测半径对估计值的影响,表示为:

i最优观测距离R=Ri,表示对应期望观测点的锋面强度最高。接下来求取期望观测点的坐标,考虑对应R的坐标集合温度预测值集合Y=R若为梯度上升搜索,则YR;若为梯度下降搜索,则将对应的作为 AUV 的第 k+1 次观测位置 xk+1。考虑AUV 的采样间隔为R0,则观测目标之间的采样路径点数记为R/R0,分布在相邻观测点所在位置之间的直线上,沿梯度方向路径点选取如图6 所示。

图6 沿梯度方向路径点选取
2.3.3 沿等温线跟踪 当AUV 沿着梯度方向运动到温度边界时,根据锋面跟踪算法,将路径规划策略切换为沿等温线跟踪。该部分将观测距离固定为R0,便于控制跟踪路径长度。本文定义跟踪等温线的路径点数量为w,那么一次等温线跟踪的路径长度为w·R0。沿等温线方向路径点选取的示意图,如图7 所示。
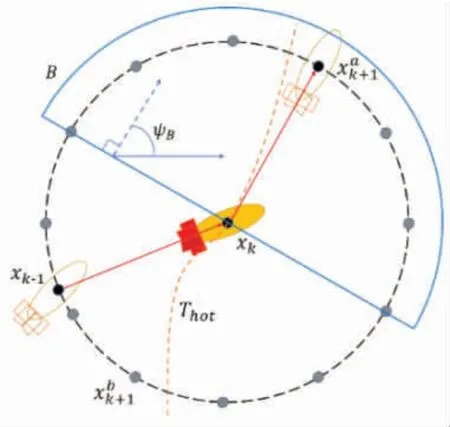
图7 沿等温线方向路径点选取
当AUV 第k 次观测到达温度边界Thot时,将采取沿等温线跟踪的动作。近邻区位置坐标集合调整为 PB_circle,温度预测值集合为 YB_circle,令选择预测值最接近Thot的位置作为新的观测点。半圆B 的方向角度为ψB,它决定了半圆内的可选观测点范围,即PB_circle。ψB的值为上次跟踪等温线的方向,即上次等温线跟踪路径上末点与始点之间的方向角,用来预测当前跟踪的等温线角度。每次AUV 切换到沿等温线跟踪的动作时,ψB都会被重新计算。当AUV 沿着等温线跟踪的累计距离为w·R0时,将重新切换为沿梯度方向跟踪。
3 仿真实验
3.1 锋面跟踪算法验证
已知观测区域A 尺寸为35 km × 45 km,设置AUV 的采样间隔R0=0.1 km,固定航速V=1.5 m/s,定义Thot=13℃,Tcold=12.4℃,路径点总数为Num=1 500(150 km),起始位置为(8,10)。在选取不同等温线跟踪长度w 的情况下,文中提出算法的仿真结果如8 所示。

图8 不同w 下本文算法仿真结果
从仿真结果可以发现,当w=20 时,AUV 在锋带弯折区域内观测较为密集,速度较慢,耗费了较多的时间;当w=25、w=30 时,算法均迅速地摆脱了弯折区域,较快地完成了锋面跟踪任务;当w=35 时,AUV 在路径点Num=1 201 时就完成了该区域的跟踪任务,但是过快的跟踪速度导致了锋面观测效率变低。
基于以上分析,本文算法通过改变w 的大小,可以调整AUV 在锋面跟踪过程中的精细观测程度。w 应根据具体任务选取一个合适的值,若要加快跟踪速度、覆盖更广的锋面区域,则适当提高w 的值;若要提高对当前区域的锋面跟踪精细程度,应适当减小w 的值。
3.2 环境实时预测效果分析
为了验证GPR 环境模型估计方法的准确性,本文利用不同时刻预测的近邻区温度场和对应的实际温度场的均方误差进行描述。均方误差的表达式为:
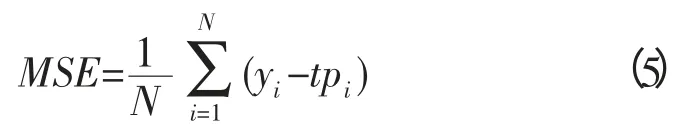
式中,yi表示预测值,tpi表示真实值。选取算法(w=25)执行期间的4 个不同时刻,GPR 不同预测半径R 对应的均方误差如图9 所示。
图中不同的Num 值描述了AUV 任务期间的不同时刻所处的位置。由上图可知,GPR 的预测半径R 越小,对环境的预测误差值越低;任务执行的越久,GPR 对环境估计的越准确。算法中的预测半径R 一般不超过0.5 km,此时预测误差量级约为10-4,可以较为准确地估计当前AUV 近邻区的温度场,表现了GPR 对锋面观测区域优秀的温度估计能力。

图9 GPR 环境实时预测的均方误差
3.3 性能分析
为了分析算法性能,将传统的锋面之字跟踪算法(简称为对比方法1)和基于最小二乘法的锋面之字跟踪算法(简称为对比方法2),与本文算法(w=25)进行对比仿真实验。本次仿真不对路径点数目进行限制,直至完成观测区域内的锋面跟踪任务。其余仿真参数不变,各算法的仿真结果如图10 所示。

图10 对比仿真结果1
由上图仿真结果可知,对比算法1 在锋面弯折区域失去了对锋面的跟踪能力,无法完成对锋面的跟踪;对比算法2 和本文算法均可在上述仿真情况下完成锋面跟踪任务。
为了比较算法的观测效率,定义了平均路径锋面温度梯度值GM,代表了单位观测路径长度上锋面所占的比重,表示为:

式中:Gi为对应观测位置的温度梯度值,采用sobel 梯度算子对插值后的温度场进行计算而得到。算法的快速性可通过任务总时间TA 来表示:

在上述仿真结果下,对比算法2 和本文算法的性能指标如表1 所示。

表1 性能指标
本文算法在观测效率上与对比算法2 相近,在跟踪速度上快了约39.4%,体现了本文算法锋面跟踪的快速性。
接下来重点考虑算法的稳定性和环境适应能力。设置Thot=13.2℃,Tcold=12.3℃,扩大了待观测的锋面区域,并将起始位置调整为(5,10),保持其他参数不变,对比算法2 和本文算法的仿真结果如图11所示。
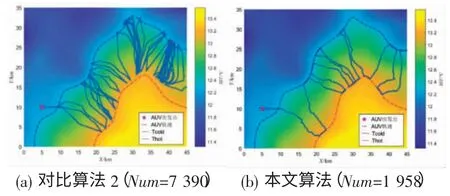
图11 对比仿真结果2
对比算法2 执行任务的过程中于3 处区域陷入了重复观测,整个任务耗费了大量时间。可以发现,当锋面的形态变化较为显著时,锋面跟踪任务要求算法具有一定的抗干扰能力。本文算法通过沿等温线(即锋区边界)跟踪,不断摆脱“陷阱”,即便边界形态变化较大,算法也能持续地跟踪锋面,并且保持了快速的跟踪速度。可见本文提出的锋面跟踪算法,具有良好的环境适应能力,且能够稳定、快速地跟踪锋面。
4 结论
本文提出了一种基于温度动态估计的AUV 锋面跟踪算法,该算法利用更新的环境信息实时预测近邻区温度分布,并根据当前位置选择不同的路径规划策略。若在锋区内部,则沿梯度方向跟踪来搜索锋面,通过实时预测的环境确定最优观测距离,从而提高锋面观测速度;若在锋区边界,则沿等温线跟踪来加速摆脱锋面,通过改变边界跟踪长度,可以实现对锋面不同程度的精细观测。使用该算法对不同观测区域的锋面进行仿真,结果显示,本文算法较于常规算法,在观测速度和环境适应能力上有更好的表现,可应用于不同锋面区域的跟踪任务。本文研究中的锋面观测区域是水平方向的,下一步计划是结合锋面在垂直方向上的特性,进行空间上的AUV 锋面跟踪算法研究。

