浅海声速剖面结构变化对声呐作用距离的影响
赵建昕,过武宏
(海军潜艇学院,山东 青岛 266199)
声呐作用距离是水声环境应用中的重要指标,对它的预报不仅依赖于声传播模型,而且还决定于海洋环境参数和目标特性。声传播速度是海洋环境参数温度、盐度和静压力的函数,是影响声传播最基本的物理参数,它的不确定性将影响声呐作用距离[1]。
笪良龙[1]以某个声速剖面为基准,利用蒙特卡洛方法获取声速剖面的不确定性,进而研究了声呐作用距离的随机分布,得到了声速的随机不确定性到声呐作用距离不确定性的传递规律。声速剖面结构变化也是一种声速不确定性的表现,它对声传播的影响巨大。这方面现有研究成果主要包括:张旭等[2]研究了声跃层结构变化对深海汇聚区声传播的影响;潘长明等[3]研究了浅海温跃层对水声传播损失场的影响;庄益夫等[4]研究了深海声速剖面结构变化对会聚区偏移特性的影响分析。李佳等[5]研究了印度洋中北部声速剖面结构的时空变化及其形成机理。谢亮等[6]讨论了海洋混合层声速剖面的结构对声传播的影响。马志康等[7]研究了台风对混合层声速剖面的扰动带来的声传播的影响。本文将重点研究浅海环境中均匀层、负梯度、正梯度和负跃层4 种声速剖面不同结构变化对声呐作用距离的影响。
1 声速剖面模型
声速剖面反映了一定范围海区的声速垂直结构,对水声传播影响巨大。针对浅海环境的特点,本文主要研究4 类声速剖面:均匀层声速剖面、负梯度声速剖面、正梯度声速剖面和负跃层声速剖面,并利用解析函数模型来模拟声速剖面,通过调整模型中的参数得到声速剖面的结构变化。
负梯度和正梯度声速剖面利用布列霍夫斯基[8]给出的声速剖面解析公式:

式中:a 为尺度参数;b 为形状参数,不同取值可以得到不同的凹凸曲线。
负跃层声速剖面,首先利用GDEM(Generalized Digital Environmental Model)模型[9-10]的幂函数形式描述海洋温跃层结构,具体为[9]:

式中:z 表示水深;A 表示跃层的平均深度;B 表示跃层中温度梯度的变化率。再次利用式(3)的线性映射得到具有式(2)结构的随深度变化的温度函数:

式中:T(z)表示温度;z1,z2为跃层顶部和跃层底部的位置,于是浅海温跃层的结构为:
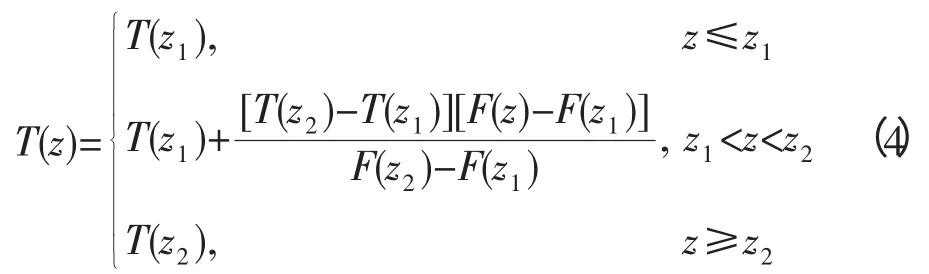
进一步,结合Wilson 公式[8]

2 数值仿真
采用Kraken 模型来计算声场,主要参数见表1,水深80 m,频率100 Hz,优质因子选择了75 dB 和80dB 两种,用来比较不同的优质因子在计算声呐作用距离时,对于声呐作用距离不确定性的影响。对于均匀层、负梯度和正梯度声速剖面,声源深度选择7 m,接收深度选择15 m。对于负跃层声速剖面,声源深度和接收深度分别选择7 m 和15 m,7 m 和40 m,15 m 和 7 m,40 m 和 7 m 这 4 种情形,旨在研究声源和接收器在跃层上、下时,对于声呐作用距离不确定性的影响。在以下的分析中,首先根据表1 中的声速剖面模型建立一个参考剖面,通过改变模型参数控制剖面的结构变化,进而讨论这些变化对声呐作用距离产生的影响。
声呐作用距离是利用非相干方法得到的声场传播损失和优质因子相等计算得到。

表1 Kraken 声传播模型的主要参数
2.1 均匀层声速剖面
选择声速为 1 510~1 528 m/s,间隔为 2 m/s 的均匀层声速剖面,见图1 的左侧子图,右侧子图给出了不同的声速剖面,优质因子为75 dB 时,对应的声呐作用距离,距离的变化范围是[8 650, 10 650]m,最大误差达到2 000 m,最大误差与声呐作用距离的最小值比为23%,可见均匀层声速剖面的误差对声呐作用距离有影响。2 m/s 的误差带来的声呐作用距离的估计误差相差200 m 以上,当优质因子选择80 dB时,距离的变化范围是[27 300, 33 550]m,最大误差达到6 250 m,最大误差与声呐作用距离的最小值比为23%,2 m/s 的误差带来的声呐作用距离的估计误差相差650 m 以上。可见随着优质因子的增加,虽然声呐作用距离大了,但是估计的最大误差在增加,原因就是声呐作用距离的估计方法,非相干方法得到的声场的传播损失曲线,如图2 所示,随着水平距离的增加,曲线的梯度绝对值趋小,带来的影响是,当声速剖面有误差代入时,同样的优质因子的声呐作用距离估计变化大,导致了上述结果。

图1 均匀层声速剖面及其声呐作用距离
2.2 负梯度声速剖面
负梯度声速剖面由式(1)获得,其中参数b 是形状参数,可用来刻化曲线的凹凸性的,选择了b=0.5,1.2 分别表示曲线上凸和下凸,不同的a 值的选择见表2,表示声速剖面在海面的声速变化大,还是海底声速变化大,见图3~图6 的左侧子图,表达了凹凸性确定情形下,不同的声速剖面,由此构成了4类不同的负梯度声速剖面。
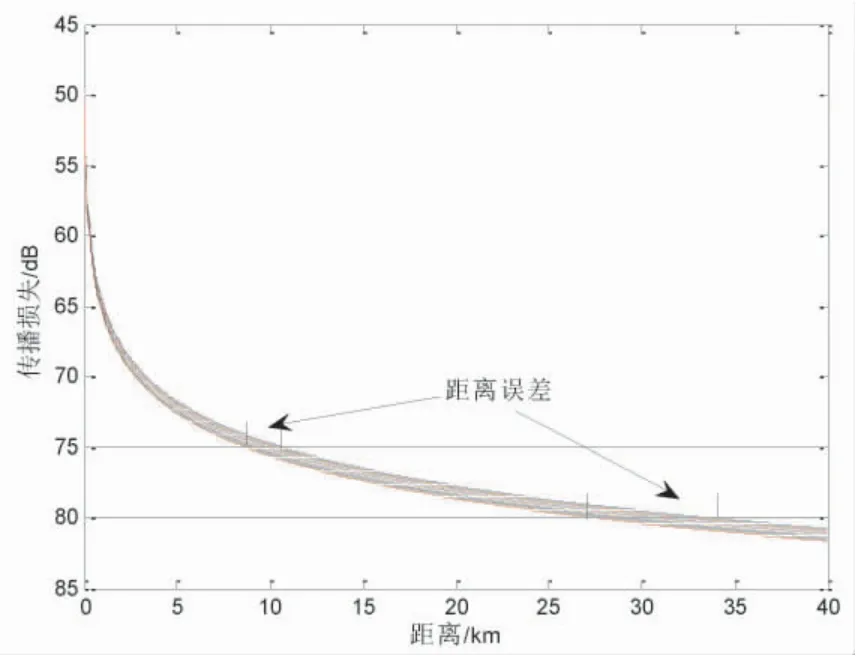
图2 均匀层声场传播损失
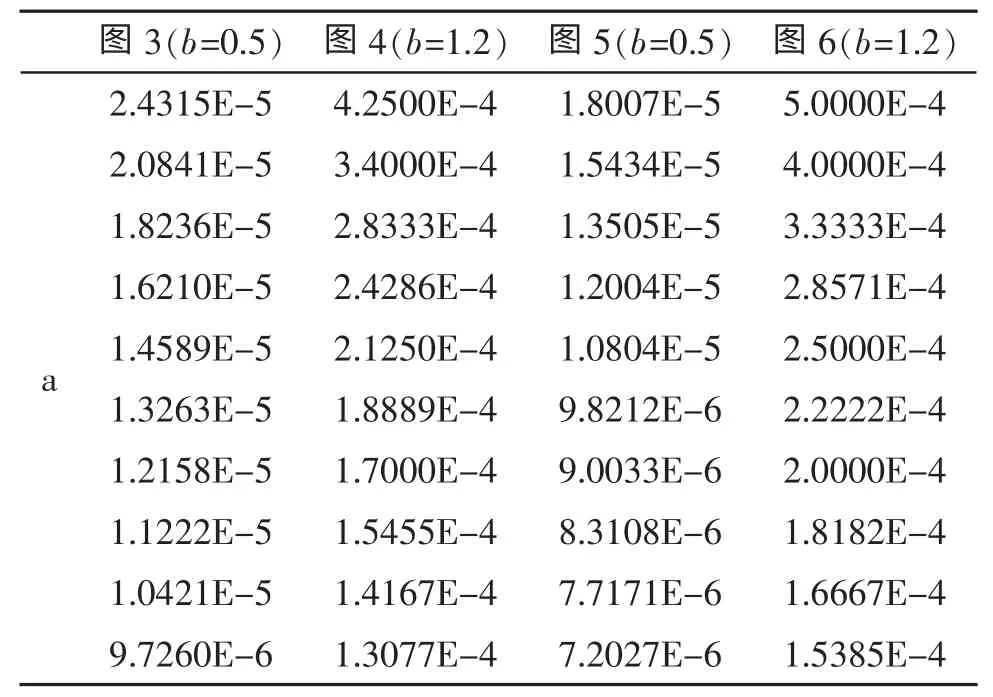
表2 负梯度声速剖面模型的主要参数

图3 上凸1 型负梯度声速剖面及声呐作用距离
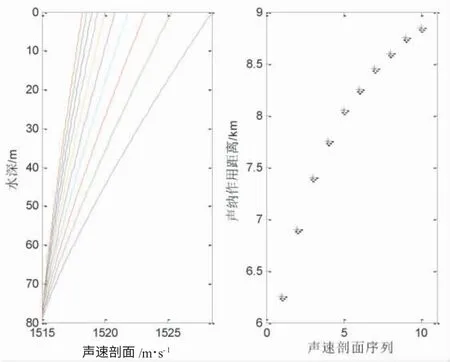
图4 上凸2 型负梯度声速剖面及声呐作用距离
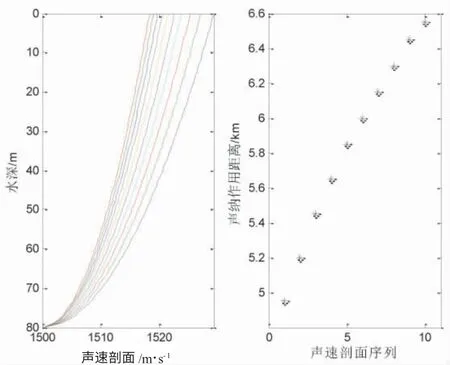
图5 下凸1 型负梯度声速剖面及声呐作用距离

图6 下凸2 型负梯度声速剖面及声呐作用距离
图3~图6 给出声源深度7 m,接收深度15 m,优质因子为75 dB 的仿真结果。各图的左侧子图是声速剖面图,右侧子图是不同声速剖面的声呐作用距离,表3 列出了4 种情形下的声呐作用距离。表3 可见,声呐作用距离范围分别是[6 350,7 050]m,[6 250,8 850]m,[4 950,6 550]m 和 [5 450,7 050]m。图3 和图5 对应的海底和海面的声速误差是一样的,对应的最大误差分别为700 m 和1 600 m,最大误差与声呐作用距离的最小值比分别是11%和32%,由此得到海面声速误差对声呐作用距离的影响更大。图4 和图6 对应的海面和海底的声速误差是一样的,对应的最大误差分别是2 600 m 和1 600 m,最大误差与声呐作用距离的最小值比分别是42%和29%,由此得到海面声速误差对声呐作用距离的影响更大。由表3 计算结果看,负梯度的声速剖面结构误差对于声呐作用距离影响大,最小的占比误差为11%,最大的占比误差高达42%。海底和海面同样的声速误差,海面的声速误差相比于海底声速的误差对于声呐作用距离影响更大。表2 和表3 实质上建立了给定参数b 取值,不同参数a 取值下,声呐作用距离的定量变化规律。此外,当优质因子增大时,声呐作用距离的最大误差有加大的趋势,与2.1 中结果类似。

表3 负梯度声速剖面下声呐作用距离(声源深度7 m,接收深度15 m)
2.3 正梯度声速剖面
正梯度声速剖面由式(1)获得,同2.2,参数b是刻化曲线的凹凸性的,选择了b=0.4,0.5,1.2 分别表示曲线上凸和下凸,不同的a 值的选择见表4,表示了声速剖面是海面声速变化大,还是海底声速变化大,由此构成了4 类不同的正梯度声速剖面。
图7~图10 给出了声源深度7 m,接收深度15 m,优质因子为75 dB 的仿真结果,表5 列出了4 种情形下的声呐作用距离。由表5 可见,声呐的作用距离范围分别是 [20 000,27 550]m,[11 200,19 950]m,[22 500,35 300]m 和[13 150,195 00]m。图 7 和图 9 对应的海底和海面的声速误差是基本一样的,对应的最大误差分别是7 550 m 和12 800 m,最大误差与声呐作用距离的最小值比分别是38%和57%,由此得到海面声速误差对声呐作用距离的影响更大。图8,图10 对应的海面和海底的声速误差是一样的,对应的最大误差分别是8 750 m 和6 350 m,最大误差与声呐作用距离的最小值比分别是78%和48%,由此得到海面声速误差对声呐作用距离的影响更大。由表5 中的计算结果看,正梯度的声速剖面结构误差对于声呐作用距离影响大,最小的占比误差为38%,最大的占比误差高达78%。海底和海面同样的声速误差,海面的声速误差相比于海底声速的误差对于声呐作用距离影响更大。表2 和表3 实质上建立了给定参数b 取值,不同参数a 取值下,声呐作用距离的变化规律。表4 和表5 实质上建立了给定参数b 取值,不同参数a 取值下,声呐作用距离的变化规律。当优质因子增大时,声呐作用距离的最大误差有加大的趋势,与2.1 中结果类似。
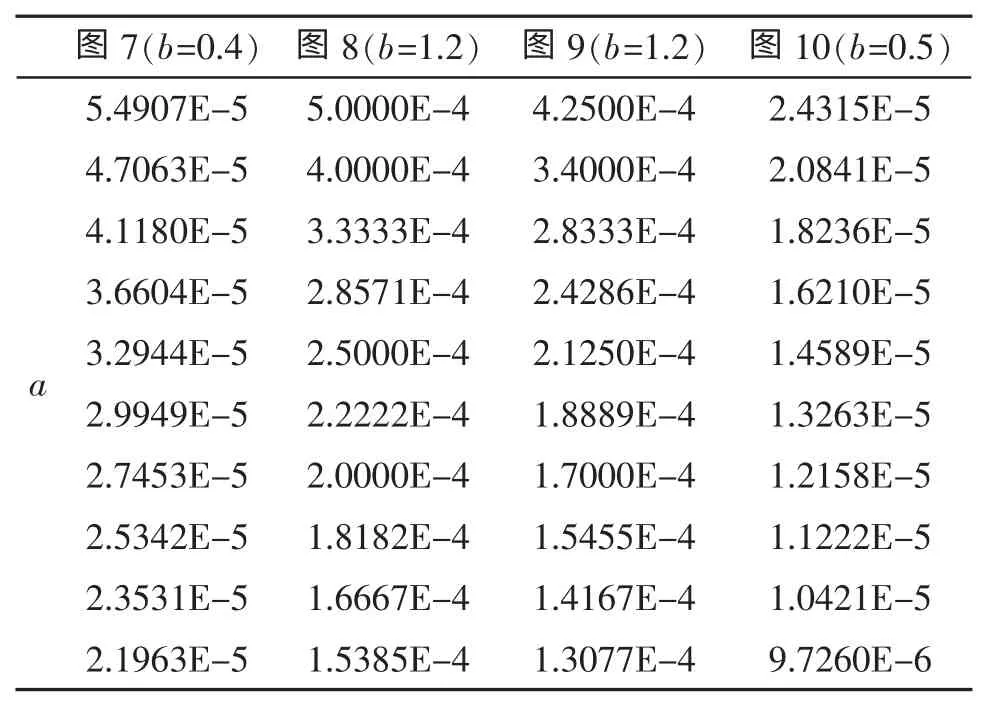
表4 正梯度声速剖面模型的主要参数
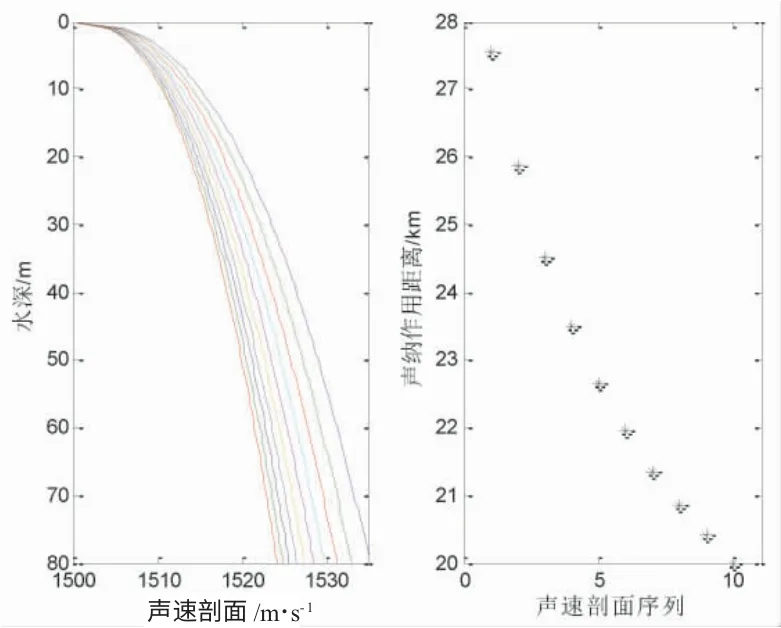
图7 上凸1 型正梯度声速剖面及声呐作用距离

图8 上凸2 型正梯度声速剖面及声呐作用距离
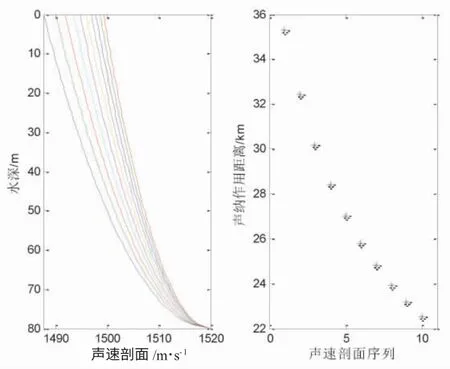
图9 下凸1 型正梯度声速剖面及声呐作用距离

图10 下凸2 型正梯度声速剖面及声呐作用距离

表5 正梯度声速剖面下声呐作用距离(声源深度7 m,接收深度15 m)
2.4 负跃层声速梯度
负跃层声速剖面由式(4)和Wilson 公式计算得到,其中参数A 表示跃层的平均深度;B 表示跃层中温度梯度的变化率。考虑了固定跃层深度,A=20的两类负跃层声速剖面,一是变温度梯度变化率B见表6 的第2 列和第3 列,分别对应不同的接收深度15 m 和40 m;二是温度梯度变化率B=2,选择不同的海表温度,即跃层以上的均匀层声速是变化的,见表6 的最后两列,对应着不同的声源深度15 m和40 m。
图11~图14 给出了优质因子为75 dB 的仿真结果,表7 列出了4 种情形下的声呐作用距离。由表7 可见,声呐作用距离范围分别是[3100,3550]m,[2800,3250]m,[3700,4600]m 和[2750,3750]m。图 11和图12 是负跃层厚度20 m,不同的接收器深度,声呐作用距离随着温度梯度变化率的变化情况,结果显示温度梯度变化率对声呐作用距离有影响。图11和图12 显示同样的声源深度下,接收器在跃层以上或以下,声呐作用距离的最大误差均是450 m,最大误差与声呐作用距离的最小值比分别是15%和16%。图13 和图14 是负跃层厚度20 m, 温度梯度变化率均为2,不同的声源深度,声呐作用距离随着跃层以上均匀层声速的变化情况,结果显示,均匀层声速的变化对声呐作用距离有影响,而不同的声源深度,分别选择15 m 和40 m,声呐作用距离最大误差分别是900 m 和1 000 m,最大误差相对于声呐作用距离的最小值分别是24%和36%,相比于接收器的误差占比,声源深度的影响更大。表6 和表7本质上建立了温度梯度变化率、均匀层声速与声呐作用距离的定量关系。
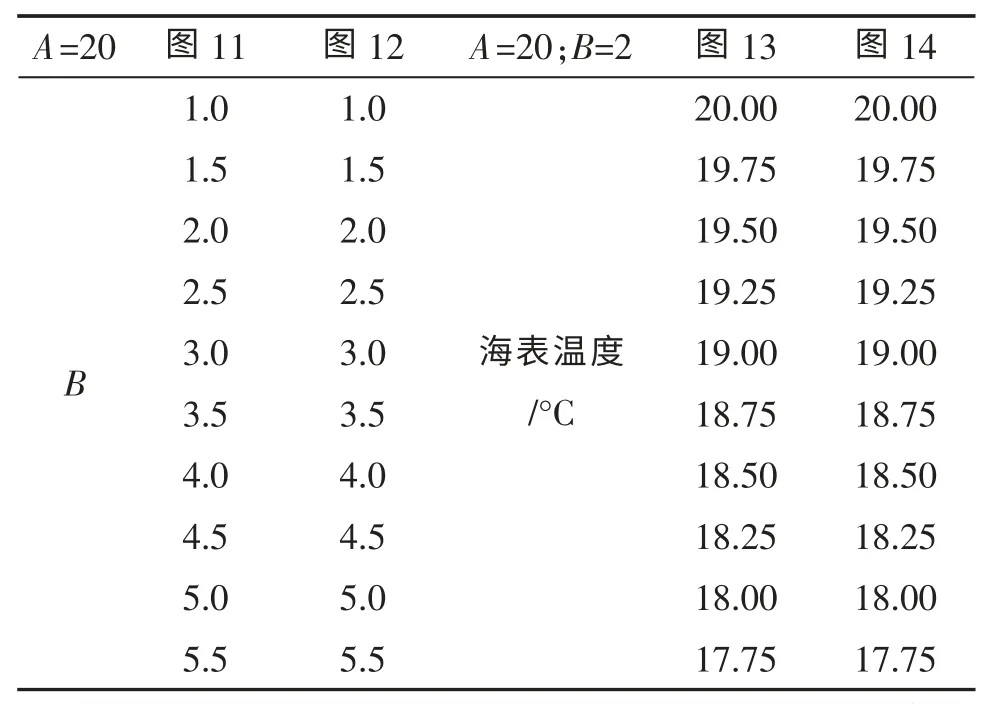
表6 负跃层声速剖面模型的主要参数

图11 变温度梯度变化率的声速剖面及声呐作用距离(接收深度15 m)

图12 变温度梯度变化率的声速剖面及声呐作用距离(接收深度40 m)

图13 变海表温度的声速剖面及声呐作用距离(声源深度15 m)

图14 变海表温度的声速剖面及声呐作用距离(声源深度40 m)

表7 负跃层声速剖面下声呐作用距离
由上分析可见,温度梯度变化率和跃层上均匀层的声速是影响声呐作用距离的两个因子,海表声速的影响大一些。优质因子增大时,声呐作用距离的最大误差有加大的趋势,与2.1 节研究结果类似。
3 结论
本文针对浅海4 种不同的典型声速剖面,通过声速剖面的数学解析函数,选择不同的参数取值,构造了不同结构的声速剖面,结合Kraken 声传播模型对于声呐作用距离进行了仿真计算。仿真结果显示,不同的声速剖面的结构变化对于声呐作用距离的影响是不同的,其中正梯度声速剖面的结构变化,对于声呐作用距离影响最大。在模拟的结果中,也显示了对于同样大小的误差,海面的声速误差相比于海底声速的误差对于声呐作用距离影响更大。对于其它频率的情形也作了仿真,结果类似。对于负跃层声速剖面的结构变化,在跃层深度不变的情况下,温度梯度变化率和跃层以上均匀层的声速是影响声呐作用距离不确定的两个因素。
此外,增加优质因子的数值仿真结果揭示了,随着优质因子的增加,声呐作用距离增大,声呐作用距离的误差也增大。这说明,优质因子增大,除了声呐作用距离增大,还需要注意估计的误差也会增大。当然,仿真不可能穷尽所有可能情形,这里给出的结果仅仅表达了论文条件下的一种认识。但是可以确定的是,在浅海环境中,声速剖面的结构变化同样会导致声呐作用距离估计的误差,这启发研究人员,在声呐的实际应用中,由于声速剖面是带有误差的,用一次观测得到的声速剖面,作为声场预报的输入,进而确定的声呐作用距离是不准确的,更合理的做法是,还应给出这个估计值的某个范围,即应该给出某个置信区间,这方面的结论还有待于理论和仿真做进一步的详细研究。

