基于混合粒子群算法的任务分配策略

张 琰，包少彬，涂双平，杨卫星

（1.南京熊猫汉达科技有限公司，江苏 南京 210014；2.南疆军区信息保障队，新疆 喀什 844200；3.联勤保障部队驻湘某预备役旅，湖南 衡阳 421216）

0 引言

多智能体系统（Multi-Agent System，MAS）是由多智能体组成的有机集合，是智能体之间的协调与协作。多智能体系统中，各智能体资源和知识是有限的，处理能力也不相同，对不同类型任务也表现出不同的适应性，所以面向多智能体的任务分配策略问题直接影响到系统的执行效率和任务目标的完成质量，所以任务分配问题也越来越受到关注[1]。

任务分配问题的研究从20世纪70年代后期逐渐展开。1980年Smith和Davis率先提出合同网模型[2]，1981年首次探讨了基于合同网的任务分配方法，对发现任务和分配任务做了定位，并讨论了解决该问题的基本思想和实现该思想的合同网技术。由此引发对合同网的研究，文献[3]在合同网模型中引入了多级协商理念，在合同网投标和评标决策过程中引入边界成本计算，文献[4]在合同网中引入熟人联盟策略，文献[5]中利用商业活动中的拍卖机制改进了合同网协议模型。1982年，Efe等人提出一种试探式的启发式任务分配模型，该方法通过综合和调整两个阶段试图得到更合理的任务分配方案[6]。1988年Lo，V.M.提出一种改进的基于图论的任务分配算法，该算法由迭代、归纳和贪心三个阶段组成，算法终止时可获得最优的分配方案[7]。1997年武汉大学何炎祥教授等人提出了基于遗传算法和模拟退火算法的任务分配算法，借鉴此两种算法的思想来解决任务分配的组合优化问题[8]。本文通过对MAS中任务分配特点的分析和研究，探讨基于混合粒子群算法的任务分配优化策略。

1 问题的提出

基本策略是先对任务或者需求进行分析和分解，再对子任务进行分配，子任务简单和较低的能力与资源要求使得原本无法解决的任务得以顺利进行。子任务往往既有依赖性的务，也存在可并行的子任务，如图1所示。

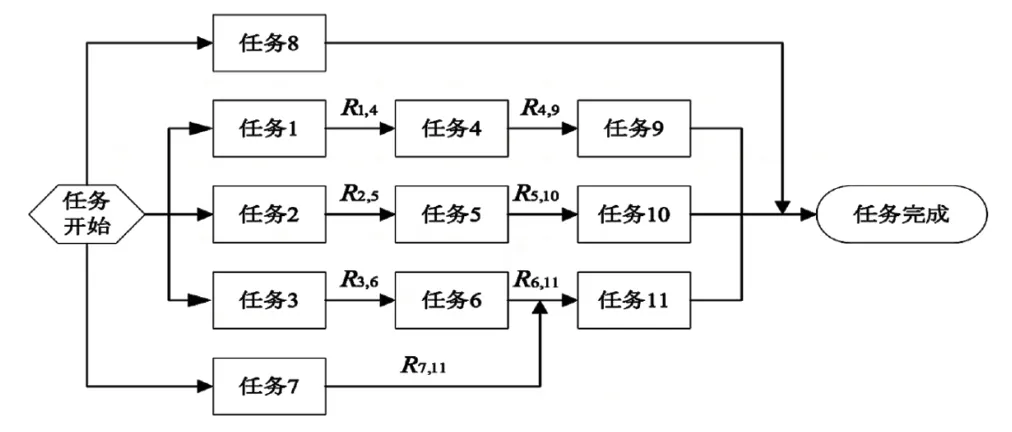
图1 子任务并行与依赖示例图

Rij表示任务j完成依赖于任务i输出，为顺序或依赖关系，任务1、4表现为该关系。任务1、2、8等任务间无依赖关系，属独立任务，为并行关系。

2 数学建模

2.1 问题描述

MAS中多目标问题可归为规划问题，可描述为：n个待完成任务T = {1，2，...，n}，需在MAS系统的m个智能体（Agent）A = {1，2，...，m}上处理完成。调度优化目标是n 个子任务在m个Agent上的运行或完成顺序最优，以使整个MAS系统总体目标（含多个目标）达到最优。为满足研究需要，做如下假设和约束条件：

⊙ 每个Agent上任务的完成顺序相同。

⊙ 给定时间内一个Agent只能处理一个子任务。

⊙ 每个子任务只能由一个Agent完成。

⊙ 每个子任务在任意Agent上处理时间已知。

2.2 数学模型

为研究需要，定义一些符号和变量下：

（1）Ti：i=1，…，n。Ti第i个子任务，T可看作任务集合。

（2）Rij：Rij=，如Rij为1表示是任务Ti优先于任务Tj，意味着任务Tj的执行必须以子任务Ti的完成为前提，可表示为Ti＞Tj（1≤i≤n，1≤j≤n），否则为0。

（3）Sij：任务Ti在智能体Ai上的执行开销。

（4）Wi：任务Ti等待处理的时间。

（5）Cij：任 务Ti所属的Agent与 任 务Tj所属的Agent之间的通信开销。

（6）Ai：i = 1，…，m。m表示Agent的总数。

（7）Dij：Dij= ，如果Dij为1，表示任务Ti分配给智能体Aj处理，否则Dij为0。

从以上定义和说明看出Ti和Ai可看作数组元素，Rij，Sij，Cij和Dij可看作矩阵中元素，所以把T和A看作数组，分别是任务集合和智能体集合，P，S，C和D分别看作矩阵，R和C是n×n矩阵，S和D是m×n矩阵。

为优化方便设计目标函数如下：

（1）执行开销目标函数：

（2）通信开销目标函数：

式中，如果k=ι，则Ck，ι=0。

（3）任务等待开销目标函数：

（4）任务完成总开销目标函数：

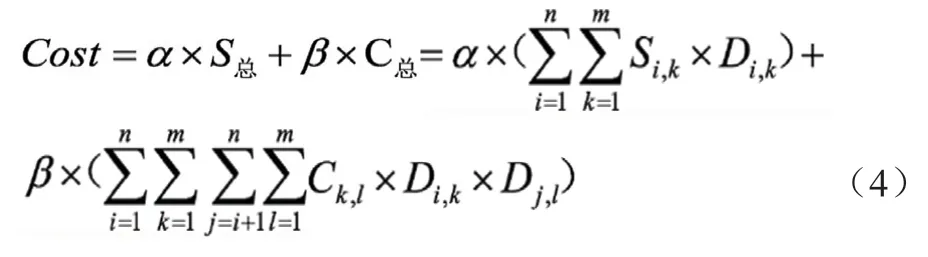
约束条件：

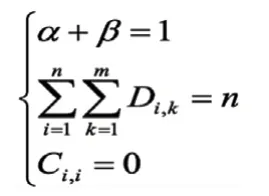
公式（4）由公式（1）和（2）组合而成，选公式（1）和（2）作为本文两个目标函数。可见把对任务分配的优化转变为对公式（4）的函数优化，Cost 值越小表明总开销越小，系统效率愈高。

3 算法设计与描述

3.1 基本的粒子群算法

基本粒子群算法中，粒子根据如下公式更新速度和新位置：

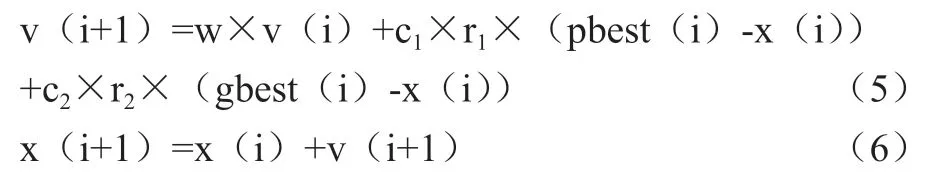
pbest（i）指个体极值，是粒子本身目前所找的最优解；gbest（i）指全局极值，是整个种群目前找的最优解。v（i）当前粒子的速度，x（i）当前粒子的位置，w惯性权重。r1和r2介于（0，1）之间的随机数。c1和c2学习因子，通常c1=c2=2。

公式（5）（粒子速度的更新公式）由三部分构成：代表粒子上一次的速度v（i）影响；代表当前粒子个体最优值pbest（i）对粒子更新速度的引导；代表当前种群全局最优值gbest（i）对粒子更新速度的引导。

3.2 改进方案

（1）基本的粒子群算法中，随着迭代次数增加，粒子更新速度越小，逐渐集中，很有可能造成局部搜索。为了一定程度上克服，参考文献[9]作出不同改进，改进公式（5）：

式中，ve代表扩展速度；λ是一个决定ve是否有效的系数，它取值为0或1，为1时ve有效，为0则无效，它以一定的概率β 取值为1。（β一般情况下值很小）。

（2）引入遗传算法中的交叉操作[10][11]。为了较快的向Pareto最优解集收敛，一定概率的选取精英库中的粒子a和粒子b做交叉操作得到粒子c，这样使得优秀粒子的优秀基因组合以可能获得更优的粒子，如果粒子c支配了精英库中的某些或某个粒子，则删除被支配粒子，加入新粒子c；如果互不支配，则加入精英库，如果精英库已满，则采用小生境策略更新精英库；如果粒子c被支配，则放弃该粒子。

本文引入PMX交叉算子作为更新方式，实现过程如下：

①已知两个父代粒子P 1和P 2（10个任务，5个智能体），从基因编码中随机取两个交叉位置点进行交叉，假定选中2，5。

父代粒子P1

父代粒子P2

②交换交叉位置点之间的基因得到两个新解C1和C2，即两个子代粒子。

子代粒子C1：

子代粒子C2：

（3）遗传算法中的变异操作[10][11]。以一定概率δ取粒子群中的小部分粒子，进行重新初始化操作来完成变异，能够一定程度上避免陷入局部极值，随着迭代次数的增加δ值逐渐变小至0。

（4）精英策略。为克服优化过程中由随机因素而导致优质解丢失问题引入了精英策略。

（5）拥挤策略。为每一个粒子从精英库中选定全局极值gbest 时，采用拥挤策略。

3.3 算法流程描述

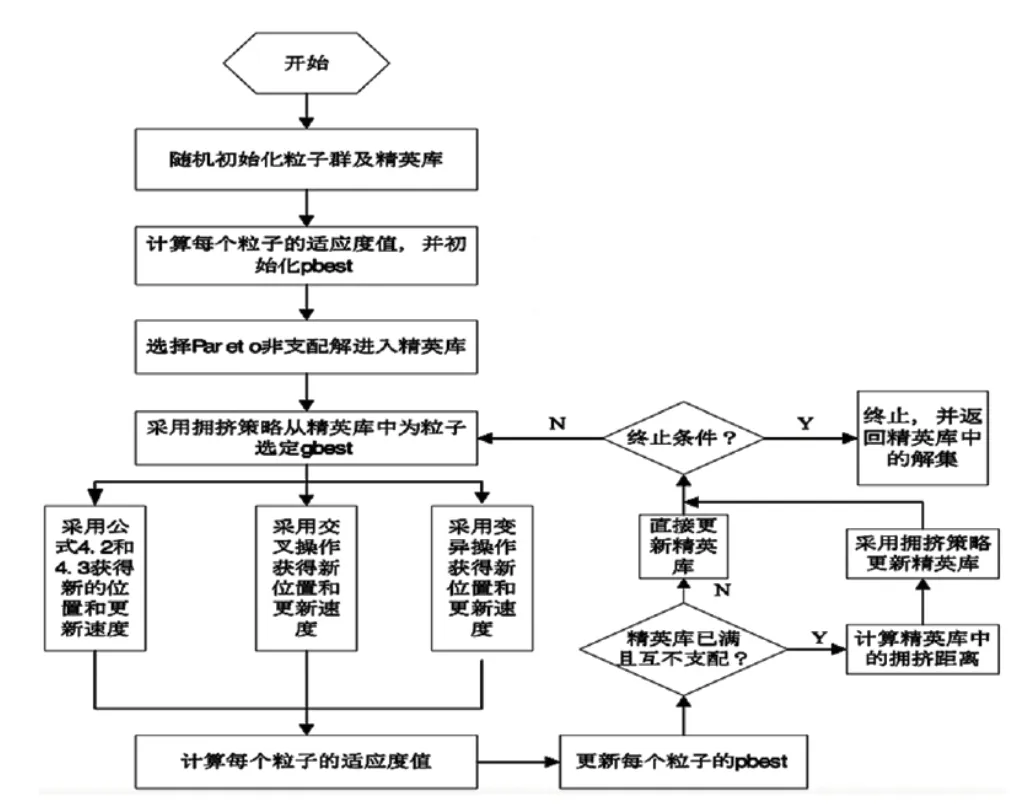
图2 多目标粒子群算法流程图

算法的基本流程：

①初始化粒子群。包括粒子群P和精英库E得规模，并初始化粒子初始位置和初始速度； 计算粒子群P中每个粒子的目标向量值。

②根据粒子的目标向量值，选取其中的Pareto非支配解放入精英库。

③为每个粒子初始最优个体位置pbest，即粒子的初始化位置。

④采用拥挤策略从精英库中随机为每一个粒子选择全局极值gbest 。

⑤采用三种方式更新粒子。采用公式3.7和3.8 更新粒子位置和速度；引入交叉操作，以一定概率选取粒子群中的粒子，随机从精英库中选取一个粒子，对两个粒子作交叉操作，获得子代粒子并替代父代P中的粒子；引入变异操作思想，从粒子群P中随机的以较小的概率选取粒子，对其进行重新初始化，已完成变异操作，在迭代后期，不再进行变异操作。

⑥约束粒子的搜索空间。如果粒子飞出了某个决策变量的界限，则粒子取该边界值，并改变速度方向。

⑦计算粒子群P中的每个粒子的目标向量。比较新粒子的位置与其自身最优位置pbest，如果新解支配了pbest，则更新pbest为当前位置； 如果pbest支配了当前粒子位置，则保持原来的pbest；如果当前位置与pbest互不支配，则随机选择其中一个作为自身的最优位置。

⑧在粒子群P中选择Pareto最优解与gbest 比较，如果存在解与gbest互不支配，或支配了gbest，则把该粒子放入精英库，然在精英库中再选择Pareto最优解留在精英库中，支配解则再次放入粒子群P中，如果来精英库已满，则采用拥挤策略删减精英库中的粒子。

⑨如果达到终止条件，则停止搜索，否则，跳转到④。

4 测试和分析

设定任务数N=20，智能体数M=10，则可能的分配策略有2010种，有使用智能算法的必要。随机初始化执行开销矩阵Execute，通信开销矩阵Comm，任务关系矩阵Rel，初始化粒子群pop，粒子数规模sizepop=30，精英库的规模为sizepop/3，迭代次数i retat ions=500，粒子的最大更新速度Vmax=M/4，最小更新速度Vmin=-M/4，粒子各个维度的边界相同，最大边界popmax=M，最小边界popmin=1。测试数据随机生成。

由图3可以明显看出粒子的初始化具有随机性，符合仿真测试的要求。

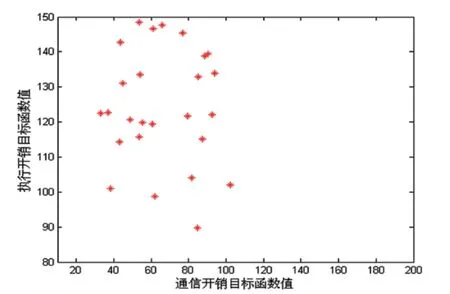
图3 初始化粒子群的适应度值分布图

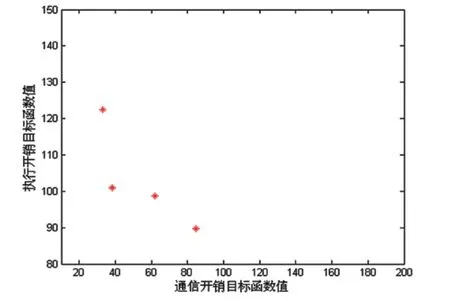
图4 初始粒子群的精英粒子目标函数值分布

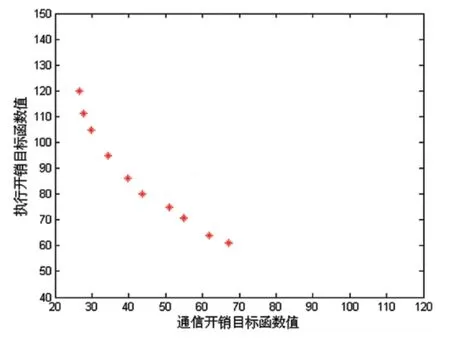
图5 优化后的精英粒子目标函数值分布图

可以明显看出，多目标混合粒子群算法进行优化后的精英粒子的目标函数值分布均匀，质量较高。

从收敛效果看，改进后的多目标粒子群算法优化后的结果优于标准的多目标粒子群算法优化后所得到的结果。未改进的粒子群算法迭代结束后得到的粒子群的目标函数值的分布有些凌乱，改进后的多目标粒子群算法所得到的粒子群的目标函数值的分布则明显比标准的粒子群算法均匀，表明了改进后算法的有效性和优越性。

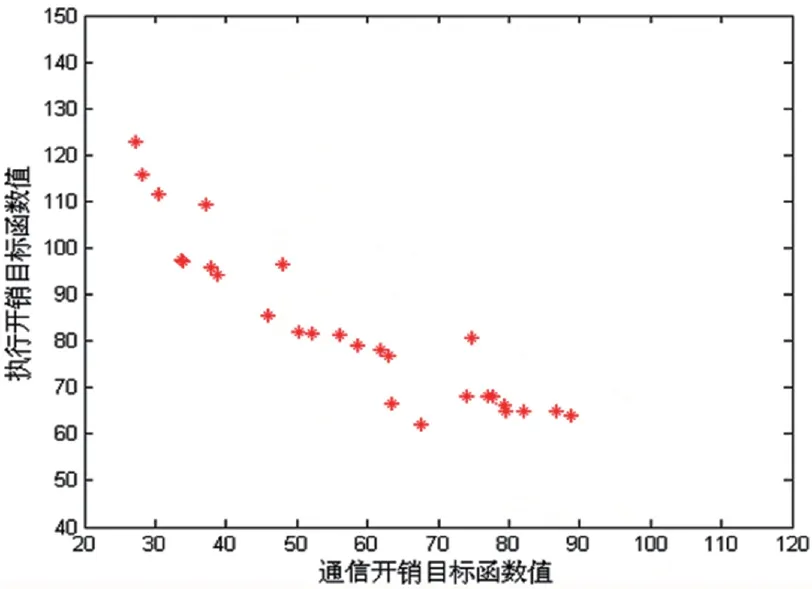
图6 标准多目标粒子群算法粒子目标函数值分布图

5 结束语

基于混合粒子群算法的任务分配策略在针对任务分配上拥有优于单独使用传统任务分配算法的巨大潜力。首先，粒子群算法本身具有特点使得在优化过程中可以较快的收敛；其次，对原公式（5）的改进，一定程度上避免了陷入局部搜索；最后，引入精英策略和交叉操作，在某种程度上保持了优质粒子，并一定程度上克服了由于随机性可能带来的优质解的丢失问题，且没有减慢算法的收敛速度。

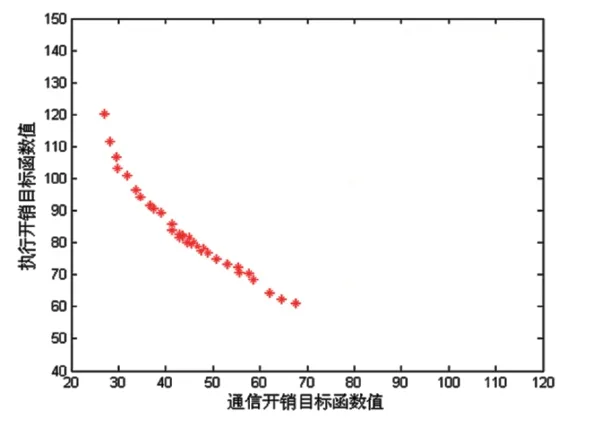
图7 多目标混合粒子群算法优化后的粒子目标函数值分布图