基于熵值和G1法的自动驾驶车辆综合智能定量评价*
李 茹,马育林,田 欢,孙 川,2
(1.清华大学苏州汽车研究院(相城),苏州 215134; 2.清华大学车辆与运载学院,北京 100084)
前言
随着计算机和人工智能等技术的不断发展,自动驾驶车辆的研究也在不断深入[1]。美国、欧洲和我国相继在举办自动驾驶车辆相关的赛事[2-3],包括:美国DARPA组织的多个自动驾驶赛事,如2004年和2005年的Grand Challenge、2007年的Urban Challenge及2012年的Robotics Challenge,比赛借助PerceptOR项目相关测评方法,以完成所有规定项目的时间长短作为指标进行评价[4-5];欧洲的ELROB自2006年起组织了连续14届赛事,比赛环境和任务设计分军用和民用两方面,更加注重车辆感知能力的考核[6];NSFC自2009年起连续举办了11届“中国智能车未来挑战赛”[7-8],具体如表1所示。此外,2010年谷歌公司研发的自动驾驶车辆实车路测[9]、2015年百度自动驾驶车辆在北京五环上实车路测[10]以及意大利帕尔玛大学的洲际挑战赛都引起关注。
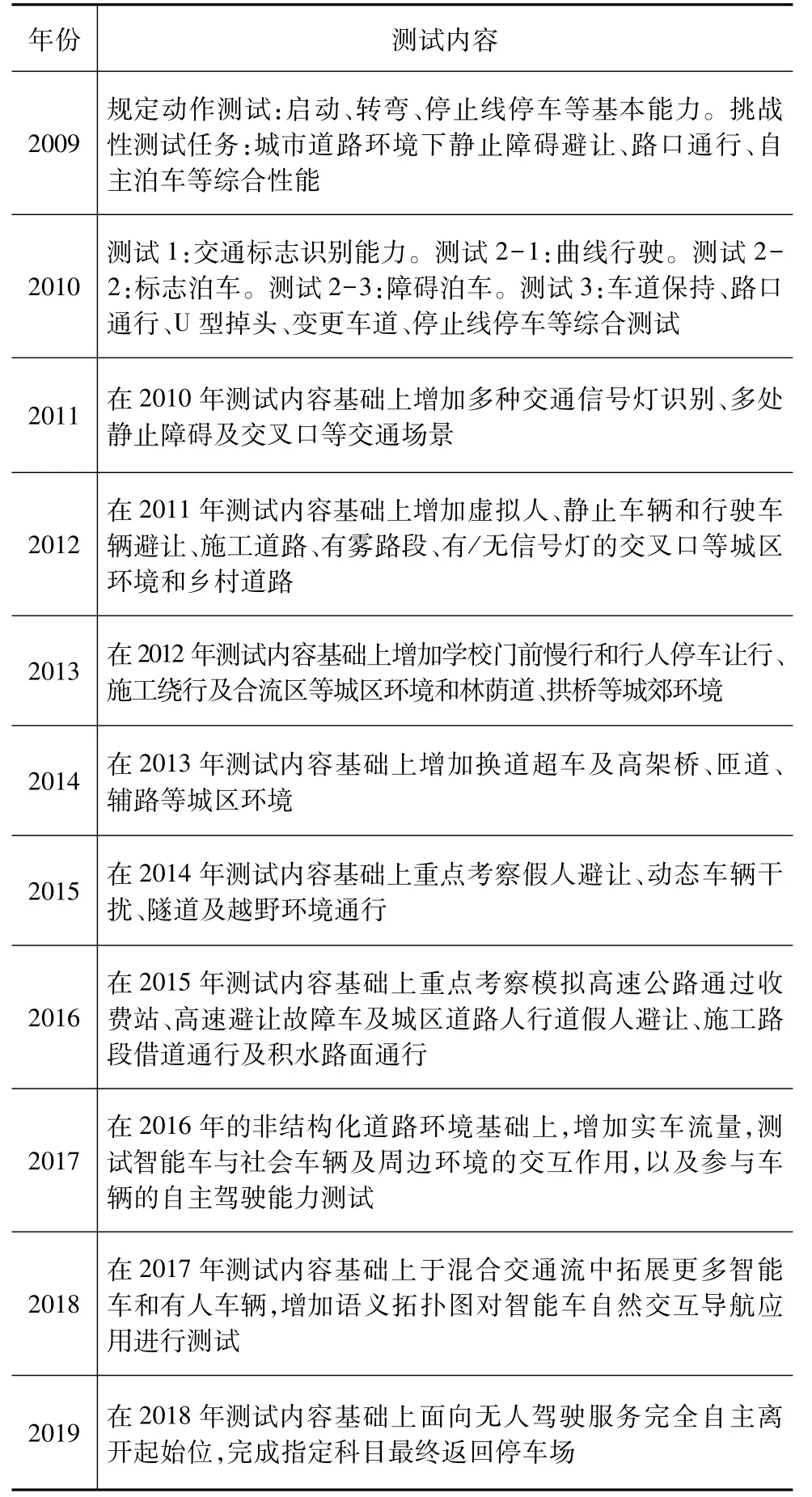
表1 中国智能车未来挑战赛测试内容
然而,不管是国内外对竞赛车辆展开的测试评价研究,还是世界各地的科研机构、高校和企业对测评体系的研究,测评规则大多按照车辆自身的特点进行设计,故而测评体系大多都是定性评价,即使是定量评价,采用的评价方法也存在很多问题,如评价维度单一、主观意识过高、科学性较弱等,不能全面、客观、准确地反映自动驾驶车辆的综合性能。文献[11]中提出了一种基于成本函数的定性与定量相结合的评价方法,该方法虽然可以完成定量评价,但此层次分析法存在判断矩阵过于明确化、一致性检验过程计算量大、盲目性等问题;文献[12]中提出一种模糊可拓展层次分析法,该方法克服了文献[11]中的不足,可避免层次分析法中繁琐的试算工作,但是该方法的评价指标体系中包含主观指标,同时采用的可拓层次分析法须对所有的评价指标进行两两比较从而构造判断矩阵,计算复杂;文献[13]中提出了一种客观赋值权法,该方法可对其评价体系中的“停车精度”、“车速保持”等指标进行客观评价,该方法不受人为因素影响,但获得的指标权重依赖测试结果和评价的对象,即指标权重的确定不具备普适性。
因此,为解决上述存在的计算量大、复杂、盲目性和普适性不高等问题,并全面、客观、准确地评价自动驾驶车辆的综合性能,必须系统地开展自动驾驶车辆行为测评的研究。提出一种熵值法和序关系分析法相结合的确定指标权重系数的方法,同时采用模糊综合评价法对自动驾驶车辆进行综合智能定量评价。通过对自动驾驶车辆进行综合测评,来评价自动驾驶车辆的安全性、系统性、平稳性和速度性4个方面的表现,从而推动自动驾驶技术的发展,进一步完善相关测评体系。
1 评价模型构建
1.1 评价指标建立
本着科学、客观的原则,结合国家出台的相关法规,主要采用从安全性、系统性、平稳性和速度性4个方面进行评价的方法。1级目标层:对自动驾驶车辆测试的评价;2级准则层:自动驾驶车辆的安全性、系统性、平稳性、速度性;3级要素层:安全性评价包括功能安全和碰撞安全,系统性评价包括感知性能、行为决策规划和控制执行,平稳性评价包括车辆操纵平稳性,速度性即为纵向速度;4级指标层即针对要素层每项要素进行具体指标评价。具体如图1所示。
1.2 熵值法
熵值法是利用所需评价指标的实际值来度量其有效信息量的多少,从而确定评价指标的相应权重[14]。熵值越大,系统信息量越小,指标权重越小;反之,系统越确定,信息量越大,指标权重越大[15]。
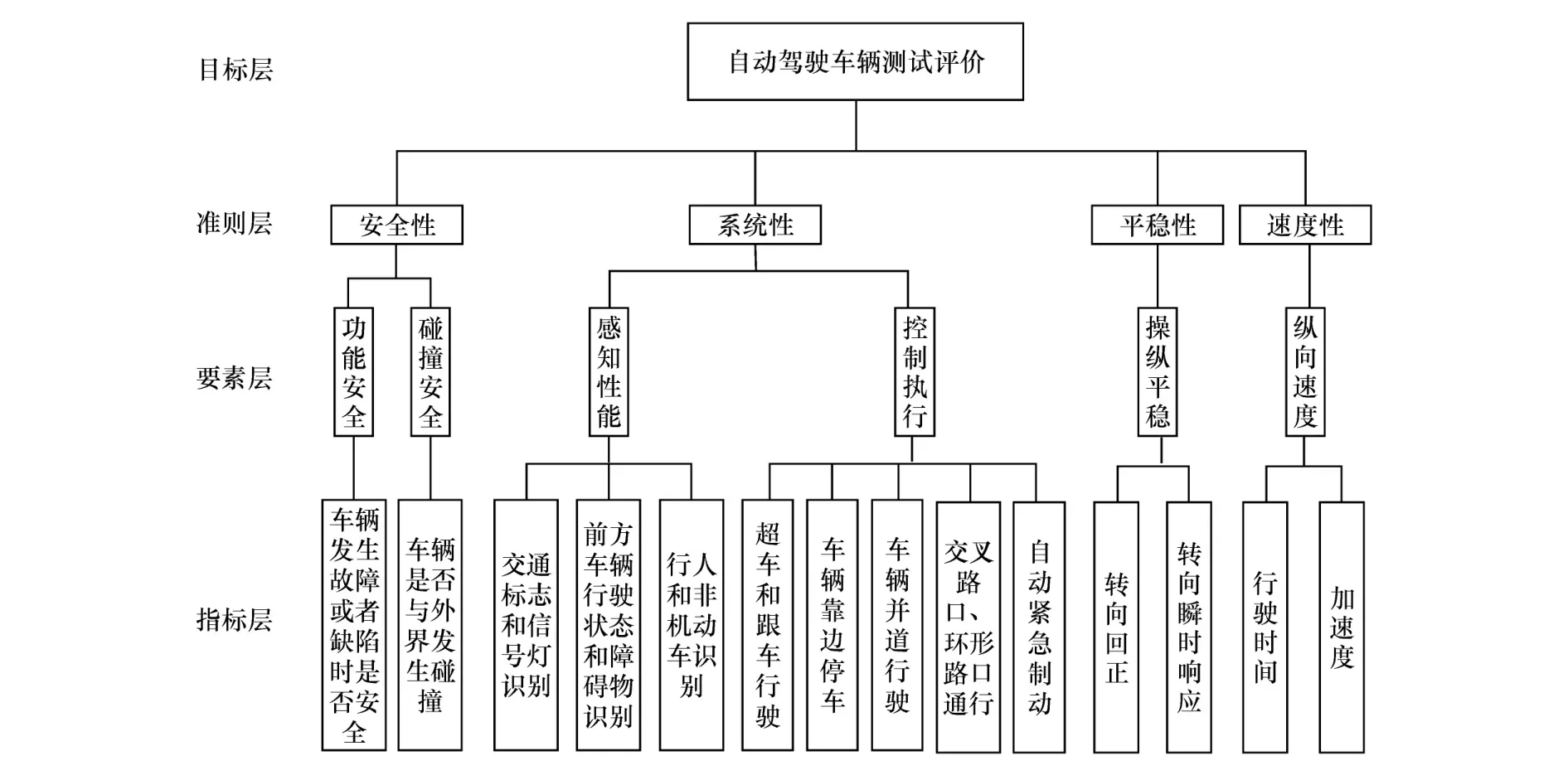
图1 自动驾驶车辆测评体系
根据熵的定义,自动驾驶车辆测试评价各层级j的第i个评价指标的熵值计算公式为

第i项指标权重的熵值计算公式为

根据熵值的性质得到:0≤wi≤1,wi=1,最终可得出评价指标权重集合:w=(w1,w2,…,wm)T。
1.3 序关系分析(G1)法
所述序关系分析法通过在指标集{x1,x2,…,xm}中将指标组成序关系,即

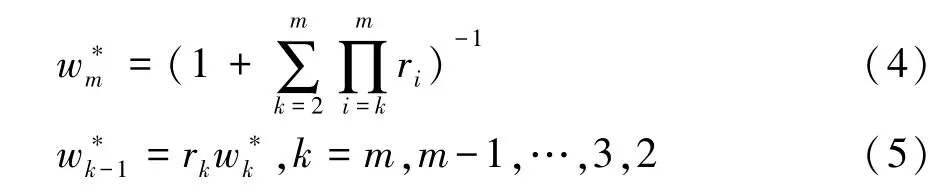

表2 序关系赋值参考表
1.4 模糊综合评价法
模糊综合评价法的自动驾驶车辆测试评价模型建立具体步骤如下。
(1)在指标体系确定的基础上,针对单因素Ui(i=1,2,3,…,m;m为因素数)进行单因素评判,得到对应的评价等级Vj(j=1,2,3,…,n;n为等级数)的隶属度cij。由此,m个因素的评价结果构成一个评价矩阵C,即确定了从U到V的模糊关系C:

一般将C按行或列进行归一化。
(2)确定权重及单因素评价模型。先通过熵值法和序关系分析法结合得到权重集R=(r1,r2,…,rm),然后将其与评价矩阵C进行合成,即得到各因素的模糊综合评价模型:
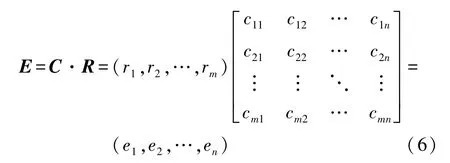
对于多层次的评价模型来说,采用多级模糊评价模型。由最下层开始计算,得到的结果组成上一级评价要素的评价矩阵,以此类推得到自动驾驶车辆测试评价模型E。
(3)计算自动驾驶车辆测试评价得分。为直观地看出评价结果,将隶属度评价等级集(好,较好,一般,较差,差)量化为分数μ。百分制计分下的综合得分S由下式计算得到。

其中μ=[1.0 0.8 0.6 0.4 0.2]。
2 指标综合权重确定
本文中通过熵值法和序关系分析法相结合确定自动驾驶车辆各级评价指标的权重,该方法有效减少了评价者的主观性,使指标权重值的确定更加合理。
2.1 李雅普诺夫指数
由于序关系分析法中确定指标间序关系时更多依赖于专家建议,故而通过李雅普诺夫指数直观地对部分指标进行量化表示,使专家评定时有可靠依据。该方法主要针对自动驾驶车辆行驶轨迹进行分析,对于非线性时间序列采用Wolf方法进行计算[16],具体步骤如下。
(1)通过车辆轨迹偏差数据时间序列{X(ti),i=1,2,…,N}计算平均周期P;
(2)计算出数据序列的时间延迟τ和时间窗口tω,从而得到嵌入维数m,其中,m=tω/τ+1;
(3)重构相空间{Yj,j=1,2,…,M},在相空间中选择每个演化相点J距当前相点I的距离差,找到最近邻点,且>P;
(4)计算相空间中相点的邻点对的i个离散时间步长后最短距离Dj(i):
(5)计算q个相点i非零Dj(i)对应的ln Dj(i),进而得到平均y(i),即
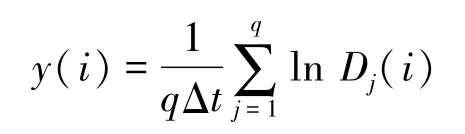
通过最小二乘法做出回归直线,直线的斜率即为要计算的李雅普诺夫指数值。
自动驾驶车辆的定位主要通过组合定位的方式获取精确的定位信息,利用车载数据采集模块获取雷达等传感器数据,进而获得自动驾驶车辆的行驶轨迹。本文中主要选取转弯和避障两个场景进行试验。通过GPS/DR组合定位技术获得自动驾驶车辆转弯和避障时的行驶轨迹,包括车辆实际行驶轨迹和规划的理想路径,对车辆转弯和避障的实际行驶轨迹与规划理想轨迹进行坐标变换得到XOY坐标系的相对坐标,坐标转换后的转弯行驶轨迹如图2和图3所示。
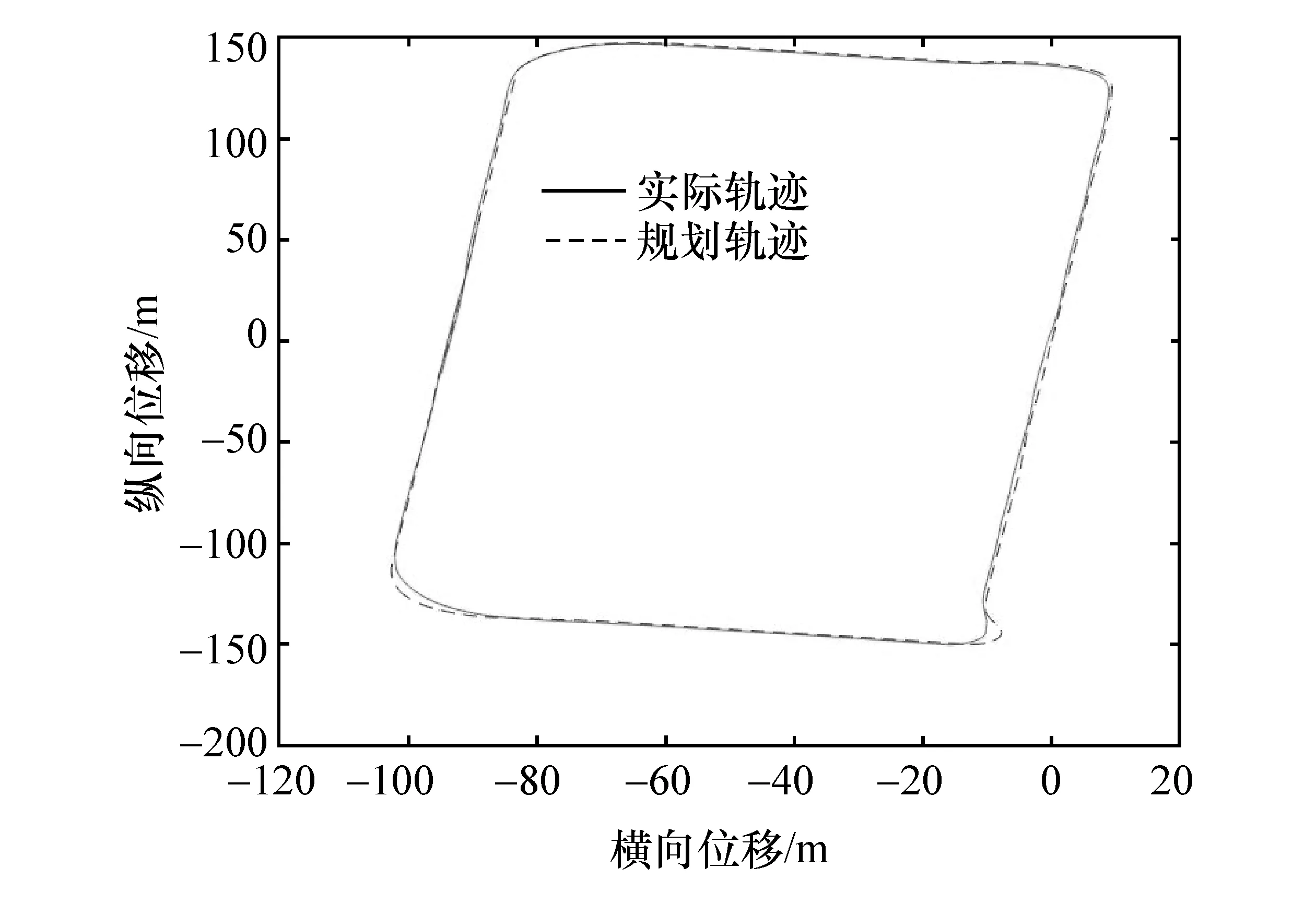
图2 自动驾驶车辆转弯场景实际与规划行驶轨迹对比

图3 自动驾驶车辆避障场景实际与规划行驶轨迹对比
在得到经坐标变换的行驶参数后,计算自动驾驶车辆理想规划轨迹和实际行驶轨迹的偏差时间序列。采用C—C方法确定自动驾驶车辆转弯和避障场景下实际行驶轨迹与理想轨迹偏差时间数据序列的时间延迟和嵌入维数,如图4和图5所示。
根据Wolf方法计算自动驾驶车辆实际行驶轨迹和理想规划轨迹的偏差时间数据序列的李雅普诺夫(Lyapunov)指数,计算结果如表3所示。
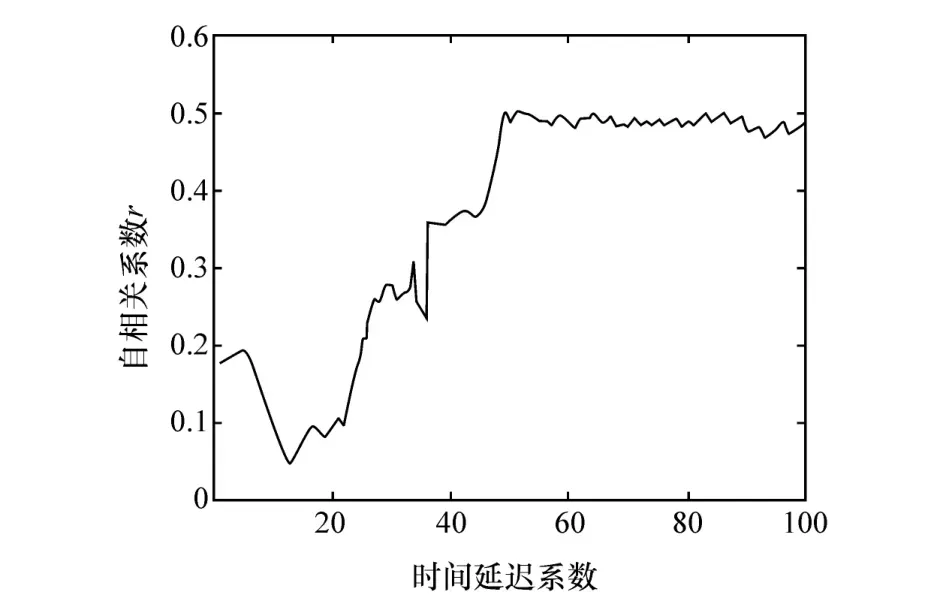
图4 转弯场景时间延迟

图5 避障场景时间延迟
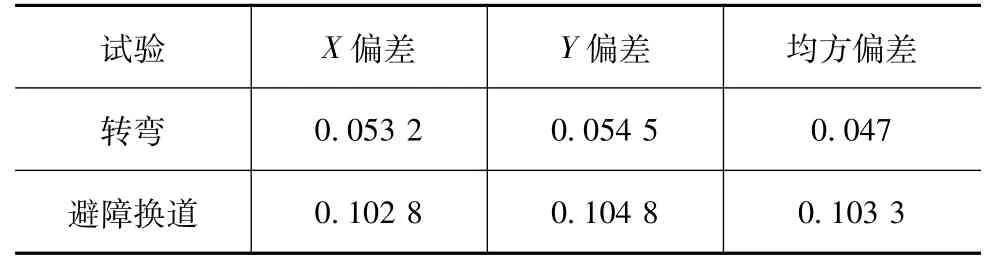
表3 自动驾驶车辆行驶轨迹的Lyapunov指数
经计算,自动驾驶车辆转弯和避障换道行驶轨迹的Lyapunov指数为正值,该指数的大小表征自动驾驶车辆收敛到稳态响应的快慢程度。自动驾驶车辆的一些场景(任务)的指标排序关系可以该指数值作为依据,指数越小则该任务表现相对越好,指标重要度也越低。
2.2 综合权重
在计算出熵值法的指标权重wi和序关系分析法的指标权重wk后,综合权重计算为

最终可得出自动驾驶车辆各级指标的综合权重为ξ=(ξ1,ξ2,…,ξn)T。
3 自动驾驶车辆综合定量评价
历年的i-VISTA自动驾驶汽车挑战赛主要包括行人避让、交通信号灯识别、施工绕行、机动车避障等比赛场景,对车辆的感知、决策等能力进行测试。现以“清华苏州猛狮”车队记录的数据为例,主要对自动驾驶车辆的系统性综合定量评价过程进行阐述。
3.1 各指标权重确定
(1)熵值法指标权重确定
自动驾驶车辆系统性测评体系有3个层级,单个指标有5种不同状态,那么由式(1)求得各层级指标的熵值,以指标层为例,具体如表4所示,从上而下,指标信息熵值为
0.397,0.498,0.311,0.418;0.59,0.498;0.586,0.64;0.379,0.655;0.202,0.472;0.397,0.379;0.558,0.59,0.431;0.586,0.64,0.311,0.558,0.558,0.586,0.59
再由式(2)求得各层级中各指标wi的权重值,即指标层权重为
0.254,0.211,0.29,0.246;0.449,0.551;0.535,0.465;0.643,0.357;0.602,0.398;0.493,0.507;0.311,0.288,0.401;0.131,0.114,0.217,0.139,0.139,0.131,0.129
同样的方法可以求得其他层级的各指标权重。
(2)序关系分析法指标权重确定
通过采用李雅普诺夫指数作为依据,并结合专家经验法对自动驾驶车辆系统性的指标层建立如下序关系:

根据理性赋值法可得指标层:1.2,1.4,1.2;1.2;1.4;1.4;1.2;1.2;1.2,1.4;1.4,1.2,1.2,1.2,1.4,1.2。由式(4)和式(5)可计算得出各评价指标wk对应的权重值为
0.17,0.285,0.204,0.341;0.545,0.455;0.417,0.583;0.583,0.417;0.545,0.455;0.455,0.545;0.245,0.412,0.343;0.079,0.065,0.158,0.11,0.132,0.19,0.266
(3)综合指标权重确定
由指标层各指标已求得的熵值法权重wi和基于序关系分析法求得的权重值wk,通过式(8)可求得各指标的权重值ξt:

表4 “清华苏州猛狮”队车辆综合评价
0.175,0.245,0.24,0.34;0.495,0.505;0.451,0.549;0.716,0.284;0.645,0.355;0.447,0.553;0.229,0.357,0.414;0.07,0.051,0.237,0.106,0.127,0.172,0.237
3.2 权重方法对比分析
针对熵值法和序关系分析法两种主客观权重确定的方法,将其与本文方法进行对比,具体如表5所示。以表4中“路口左转弯”、“路口右转弯”和“主动超车”指标为例,主要从权重系数和评价结果两方面进行对比,权重确定方法的不同影响最终评价结果。
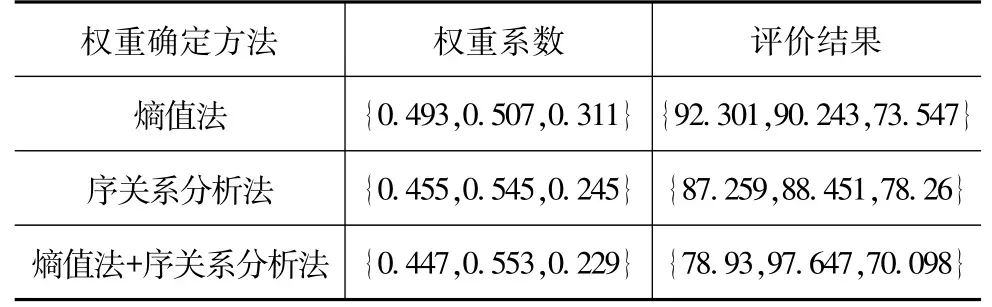
表5 权重方法对比分析
由表5可知,前两种权重确定方法可直观看出评价结果与实际评判结果{80,100,70}相差较大,而本文引入了李雅普诺夫指数,将车辆行驶过程中的横向偏差考虑在内,同时把两种方法结合后的评价结果与实际评判结果更为一致,从而可以证明该方法比原两种方法更为准确、可靠。此外,对于权重系数由于涉及到多层次综合评价,故而权重系数仅对于所属同一层级或类别时有比较关系。
3.3 综合定量评价
自动驾驶车辆系统性综合定量评价主要包含2个评价准则,每个准则中又包含不同的要素,逐层向下,隶属度评价等级集为:V={v1,v2,v3,v4,v5}。
先从指标层开始逐层向上评价,此处以“路段行驶”要素的指标层为例进行综合计算。
(1)构建“路段行驶”要素的评价指标集

(2)构建“路段行驶”要素的评价矩阵C24
评价矩阵主要是依据10位专家和专业知识得到,并通过隶属度方法进行表示,即为

(3)构建“路段行驶”要素的权重矩阵R24

(4)计算“路段行驶”要素的综合评价结果
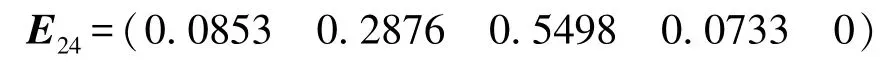
同样地,可以分别求得要素层中其他要素的综合评价结果:
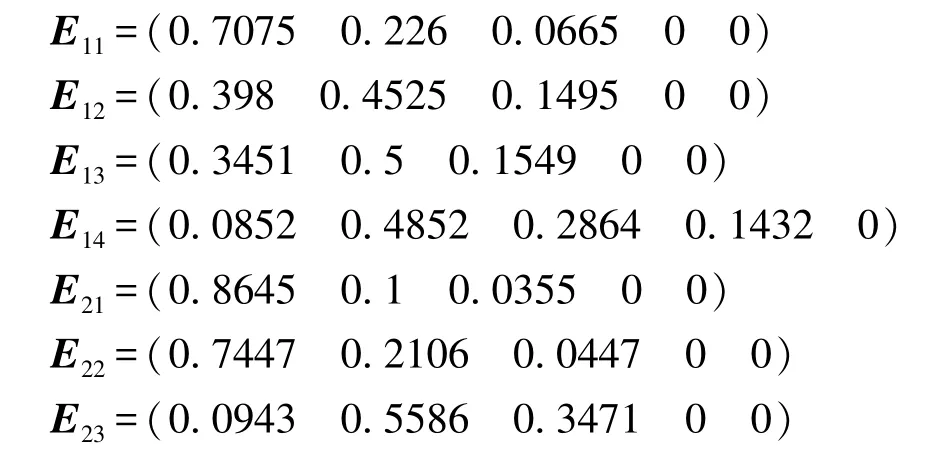
(5)计算“控制执行”准则的综合评价结果E2
与计算“路段行驶”要素的方法相同,向上计算“控制执行”准则的综合评价结果为

(6)计算车队单因素和综合评价分数
自动驾驶车辆系统性综合定量评价的2个准则:感知性能和控制执行,构成最上层的权重矩阵R为

由此可以计算出目标层自动驾驶车辆系统性综合定量评价的综合结果:

那么可以计算出参赛车队在感知性能和控制执行两个准则的分数为

最终可以得出综合的评价分数:
S=83.046
通过分数可以直观看出,该车队总体表现较好,感知性能方面的分数比控制执行方面的分数高,这是由计算的权重系数影响的。虽然控制执行方面在加速和制动等执行器上存在响应误差,导致得到的分数不高,但根据3.2节对提出的评价方法分析比较以及车辆自身的实际情况得出所提出的评价模型,结果是符合实际评判结果的。
4 结论
基于熵值法和序关系分析法相结合确定自动驾驶车辆各级指标的权重,不仅减少了如层次分析法等方法带来的计算量大,又能灵活地将主客观进行统一,同时在序关系分析法中确定指标间序关系时,通过李雅普诺夫指数直观地对部分指标进行量化表示,在一定程度上降低主观性,使评定依据更加准确、可靠。

