严格避撞的车辆队列分布式鲁棒控制*
杨泽宇,黄 晋,胡展溢,谢国涛,钟志华,2
(1.清华大学车辆与运载学院,北京 100084; 2.中国工程院,北京 100088)
前言
车辆编队行驶是一种提高道路通行率、降低行驶能耗、提高交通安全的有效途径[1-2]。随着车车通信(V2V)、车路通信(V2I)、先进车载传感器和智能控制等智能网联技术的发展,队列中车与车之间可实现信息交互,并通过智能控制技术实现协同编队行驶,从而实现更小的车间距,进一步提升交通效率和燃油经济性[3-4]。保证车辆一致行驶速度和期望空间构型的队列协同控制技术是智能网联车辆队列的关键技术,直接影响到队列安全性。
从控制器设计的角度来看,稳定性是系统的基本性能。文献[4]中针对具有对称通信拓扑的非匀质车队,基于3阶线性模型设计了分布式控制器并分析了队列的鲁棒稳定性。Zheng等基于分布式模型预测控制理论,为具有非对称通信拓扑的队列设计了满足一致稳定性的队列控制器[5]。然而,车辆队列是一个多车互联耦合系统,每辆车的稳定性并不能保证队列中所有误差状态的有界性,进而无法保证队列安全性。因此表征误差或外部干扰不沿着队列向两端扩增性质的队列稳定性也得到了广泛研究[6-9]。文献[8]和文献[9]中讨论了通信时延、动力学不确定性条件下队列稳定性的充分条件。
然而,队列稳定性给出的是平衡点附近的局部稳定特性,稳定区域边界很难显示求解[10]。因此为保证队列避撞性,初始误差应保证在平衡位置附近。文献[11]中提出了一种修正的固定车头时距模型,将队列稳定性扩展到大初始偏差条件,由于忽略了控制过程中的超调、收敛速度等瞬态性能,仍存在安全隐患。Huang等采用双射函数将有界的车间距误差转换为无约束状态,并通过非线性鲁棒控制保证了转换状态的有界性,理论上保证了队列的避撞性与紧凑性[12],但是该方法很难适用于具备复杂通信拓扑的队列。
基于以上分析,本文中针对具有复杂通信拓扑以及有界动力学不确定性的车辆队列,提出了一种严格避撞的分布式鲁棒控制方法。将队列的避撞性与紧凑性描述为对车间距误差的有界约束。引入车间距势函数,并将势函数的偏导项添加到鲁棒控制器中。根据LaSalles不变性原理证明了势函数的有界性(保证了避撞性和紧凑性)以及车速误差的队列稳定性。提出了修正期望车间距模型,保证了控制算法在大初始误差工况下的适用性。最后通过数值仿真验证控制算法的有效性。
1 系统建模
智能网联车队的分布式控制问题如图1所示。该队列包含n辆车,依次标号为1,2,…,n。xi、li分别表示第i(i∈χn,χn={1,2,…,n})辆车的位移和车身长度。di表示第i(i∈χn且i≠1)辆车与其前车的距离。假定每辆车都具备V2V、V2I功能,且装载全球定位系统(GPS)、惯导设备和自主式传感器。GPS和惯导设备可用于准确测量自车的速度、加速度等状态信息。自主式传感器(毫米波雷达等)可用于测量自车与前后车的距离[13]。具体的控制流程为:位于云端或队列中某车上的中央控制器(图中虚拟头车)通过集中式优化计算得到队列期望速度曲线,并通过V2I或V2V间歇地发送给每一辆车(图中虚线)。另外每辆车能通过V2V获取邻近车辆的实时状态信息(图中实线)。每辆车基于这些信息并结合测得的自车状态信息,生成分布式控制率,实现队列车速的稳定跟随与车间距的保持。
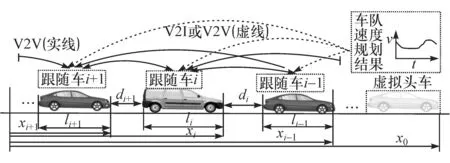
图1 车辆队列巡航示意图
1.1 车辆动力学模型
考虑到实际车辆动力学参数很难被准确辨识,同时还存在复杂的外部干扰,因此建立如下包含复杂不确定性与外部干扰的2阶非线性车辆纵向动力学模型为:
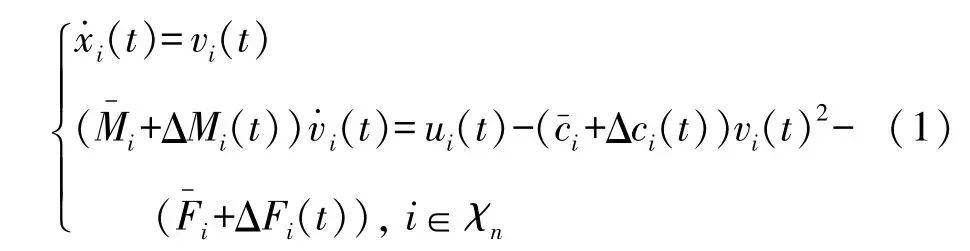
式中:vi、ui分别为车辆速度和控制力输入;分别为车辆质量、风阻系数和外部阻力(包含坡道阻力以及轮胎阻力)的名义量,它们对应的不确定量分别为ΔMi、Δci、ΔFi,这些时变不确定量关于时间t连续。
期望速度vr对每辆车都是已知的,因此可分别定义t时刻的车辆位移误差和速度误差为
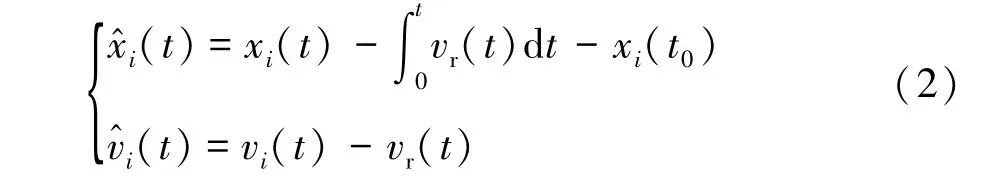
结合式(1)车辆的纵向动力学模型,误差动力学方程可表示为
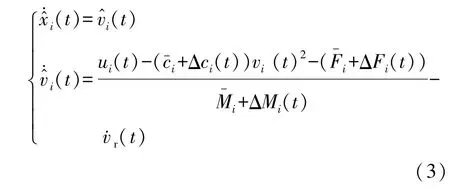
为公式简洁性,在不产生混淆的前提下,下文出现的符号将省去括号里面的参数,并定义如下符号:
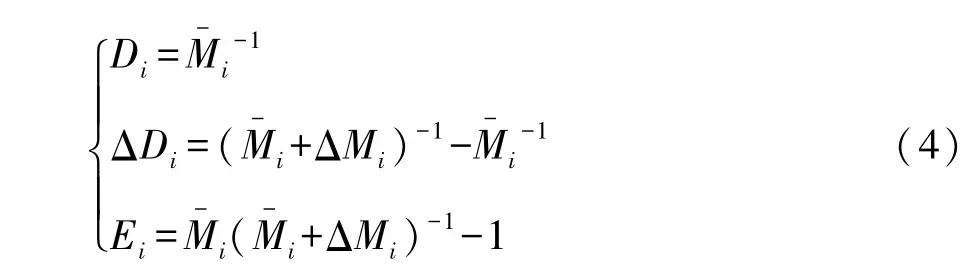
则有ΔDi=DiEi
为简化后续推导,结合式(4),将式(3)描述的误差动力学模型解耦为名义动力学和不确定动力学两部分,可得

1.2 通信拓扑模型
所有的成员车辆间歇地收到队列的期望速度曲线,还能实时获取其周围车辆的状态信息。假设具备理想的通信条件,即无通信量化误差、时延与丢包现象。代数图论技术常被用于描述车辆之间信息传递的信息流拓扑关系[13-14],将车辆抽象为顶点集χn,车辆之间的通信通道抽象为边集ϑn=χn×χn,有向边(i,j)表示车辆i可以获得车辆j的信息,则整个队列的通信关系可描述为加权有向图的结构,其中An=为邻接矩阵,定义为
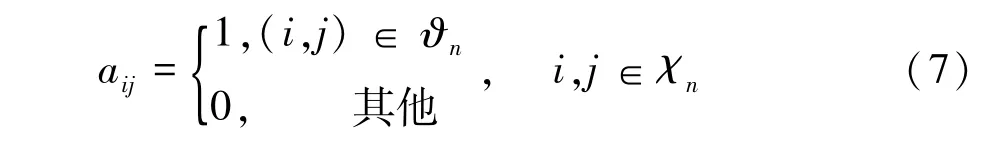
式中:aij=1表示车辆i能获得车辆j的信息。设定aii=0,i∈χn。与有向图gn对应的Laplacian矩阵为L=[lij]n×n,定义为

若有向边(i,j)∈ϑn等价于(j,i)∈ϑn,称该图为无向图。无向图对应的Laplacian矩阵是对称的,其描述的通信拓扑关系称为对称通信拓扑。
这里列出如下几种典型通信拓扑结构的邻接矩阵及对应的Laplacian矩阵。
(1)单向前车跟随(PF):车辆只能获取其前车的信息。

(2)双向前后车通信(BD):车辆能够获得其前后车的信息。
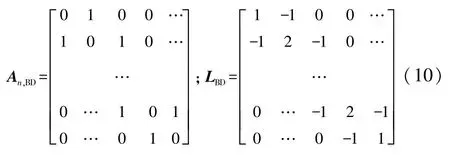
(3)双向前后两车通信(BDD):车辆能够获得其前后各两辆车的信息。
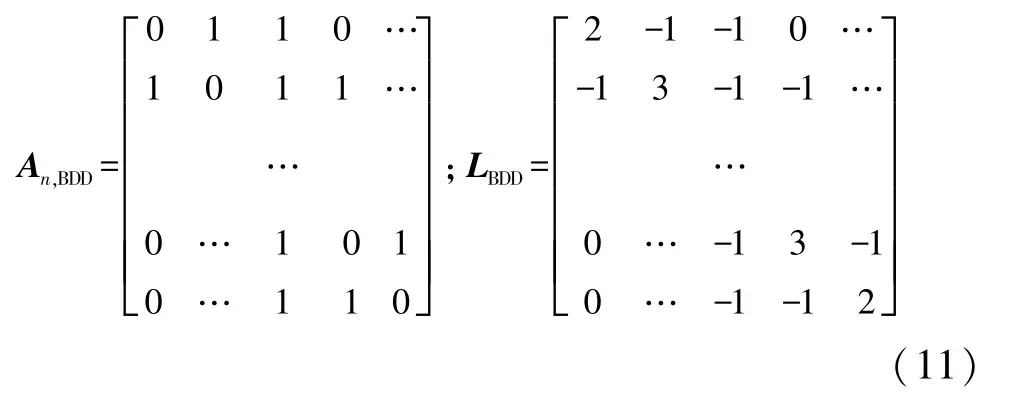
1.3 车间距模型
实际控制过程中使用的车间距数据是通过自主式传感器直接测得。但是在控制器设计过程中,实际车间距采用前后车的位移以及车身长度定义:
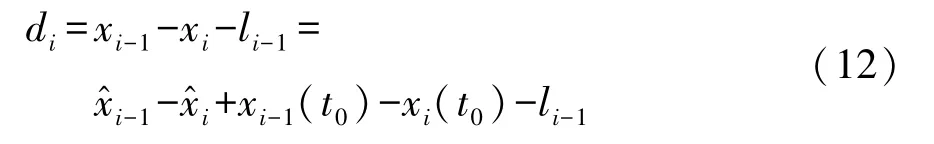
固定车间距模型相比于固定车头时距模型能实现更高的交通流量[15],因此本文设置期望车间距为一个固定的常数。车间距误差定义为
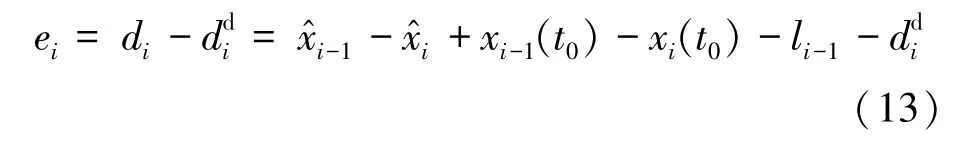
为严格保证队列安全性,同时避免队列过于稀疏(保证紧凑性),设定允许的车间距误差区间为

式中ei,m、ei,M分别为最小、最大允许车间距误差,且满足ei,m<0<ei,M。当车间距误差始终保持在允许的误差区间内时,队列安全性以及紧凑性得以保证。
1.4 车队控制目标
在给出车队控制目标以前,首先引入以下相关定义。
定义1:对任意的t≥t0,i∈χn,若车间距误差满足ei(t)∈( ei,m,ei,M) ,则称车辆队列是严格避撞且紧凑的。
定义2:对任意的t>t0,σ>0,i∈χn,若存在一个实数δ>0,使当ei(t0)∞<δ,i∈χn时,有supiei(t)∞<σ成立,则称车辆队列误差的平衡点(ei=0,i∈χn)是队列稳定的[7]。
定义3:考虑一个维数为n×n实数矩阵X,若对任意的n维向量v∈Rn,有vTXv≥0,则称矩阵X是广义半正定的。
不同于其他队列控制研究,控制目标中要求车速误差以及车间距误差都能严格收敛到0[4-5,8-12]。本研究的控制目标为:(1)车辆队列的严格避撞性及紧凑性;(2)车辆速度误差的队列稳定性。即:保证车间距误差保持在安全性与紧凑性限定区间( ei,m,ei,M) 内的前提下,实现期望速度曲线的稳定跟随。因此本文引入车间距势函数Ui,i-1,其具备以下性质:
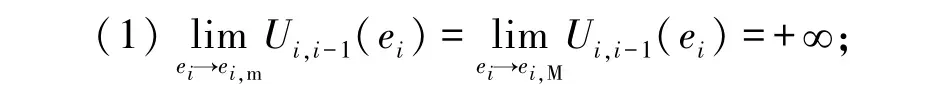
(2)Ui,i-1(ei)≥0,当且仅当ei=0时取等号;
(3)Ui,i-1(ei)1阶连续可导;
(4)当ei>0时,有>0;当ei<0时,有<0。
采用正切函数设计如下满足上述条件的车间距势函数:
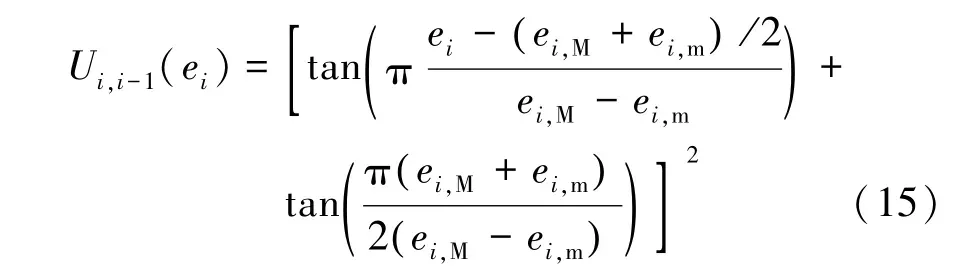
根据车间距势函数的性质,可以得到:Ui,i-1的有界性等价于ei∈( ei,m,ei,M) 。只要设计的控制器能保证Ui,i-1的一致有界性,就能保证队列的避撞性与紧凑性。
2 分布式鲁棒控制器
2.1 控制器设计
当获得队列期望速度曲线、邻近车辆状态以及自身状态信息后,每辆车须根据预设的分布式控制率,计算纵向控制力输入。由于车辆队列系统具有时变动力学不确定性,因此设计的控制器需要具备较强的鲁棒稳定性。针对式(5)中的名义动力学部分,首先设计如下两部分控制力:
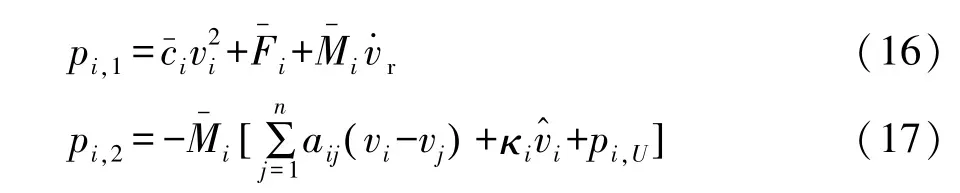
式中κi>0,为可调控制参数。
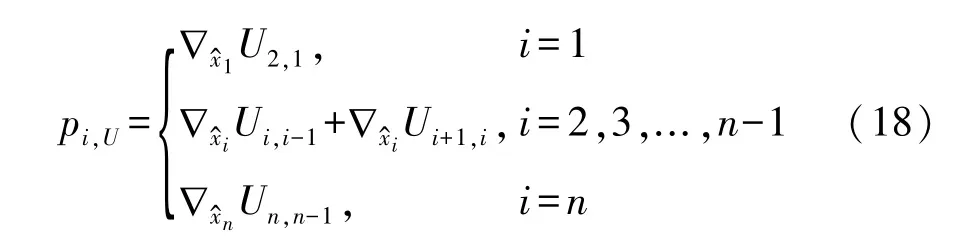
式中∇为偏导符号,例如∇x^1U2,1表示U2,1关于x^1的偏导数。针对式(15),式(18)中的各项分别为
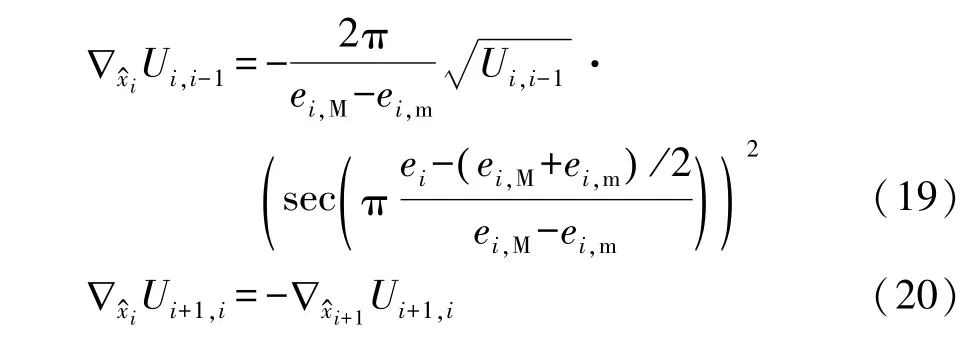
pi,U只与紧邻车辆有关。对队首(队尾)车辆,pi,U只包含后车(前车)车间距势函数产生的控制项;对队列中间车辆,pi,U是前后车间距势函数综合作用的控制量。通过车载自主传感器测得实际车间距后即可获得控制项pi,U。当ei=0时,pi,U=0,不施加调整间距的控制力;当ei≠0时,-为使车间距势函数减小的控制力,且误差偏离零点越远,该控制力越大。因此在-的作用下,车间距势函数可以维持在一个较小值,进而保证车间距停留在允许区间内。
控制力pi,1+pi,2已经能够保证式(5)中的名义动力学系统的性能。为处理动力学不确定性部分,首先给出如下两个合理假设。
假设1:对任意的t>t0,存在一个已知的常数ρEi>-1,使Ei(t)>ρEi。
基于以上假设,设计控制量为
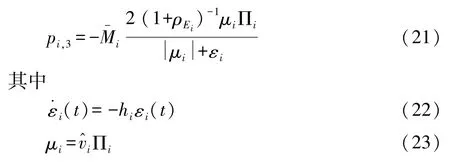
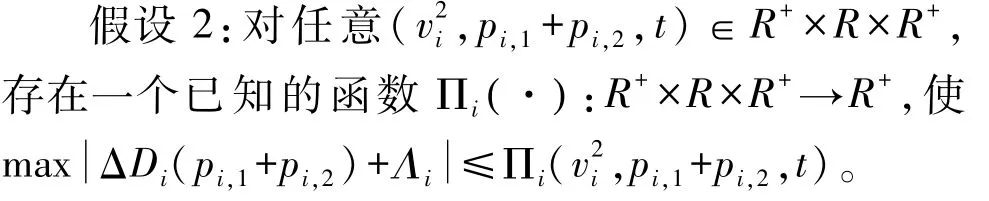
式中:εi(0)>0;hi为正常数。
总的控制力为

定理1:对任意包含有界不确定性的车辆队列系统(式(3)),如果其通信拓扑对应的Laplacian矩阵是广义半正定的,那么在控制器ui,i∈χn的作用下,该队列是严格避撞且紧凑的,同时速度误差是队列稳定的。
证明:选取如下李亚普洛夫函数
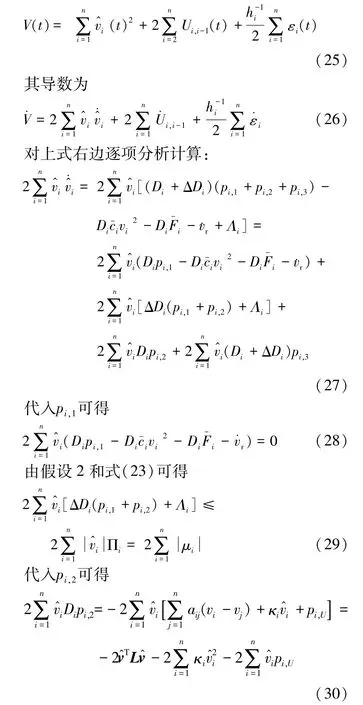
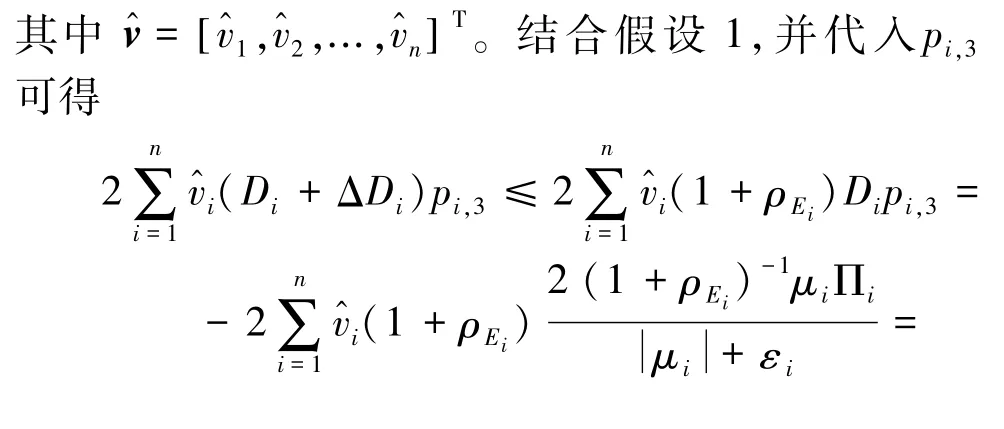

根据势函数的定义,式(26)右边的第2项为
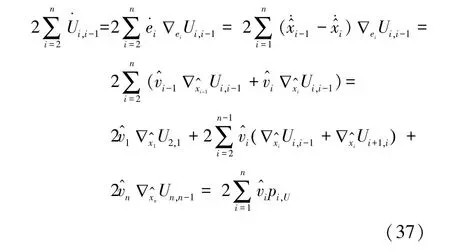
由式(22),可得式(26)右边的第3项为
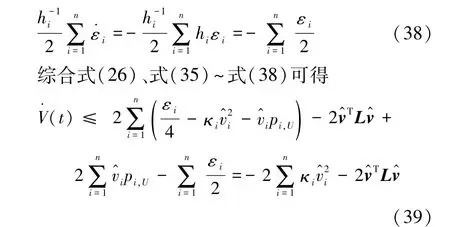
2.2 设计分析
特别地,对具备对称通信拓扑的队列,有以下推论。
推论1:对任意包含有界不确定性的车辆队列系统(式(3)),如果其具备对称通信拓扑,那么在控制器ui(i∈χn)的作用下,该队列是严格避撞且紧凑的,同时速度误差是队列稳定的。
证明:根据Laplacian矩阵的定义可得
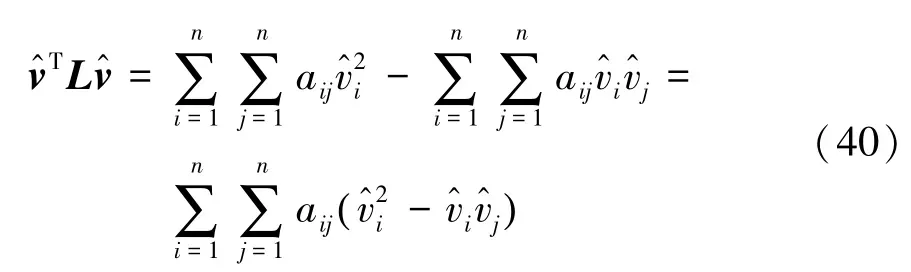
若队列具备对称通信拓扑,由其对应无向图的对称性可得
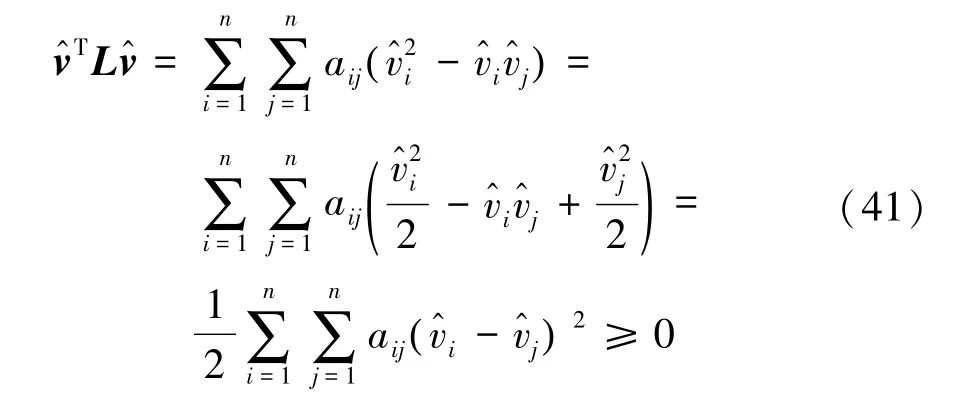
定理1只给出了该控制框架下满足队列性能的充分条件,并非必要条件。由式(39)可得,V·(t)的大小还与κi有关。对于满足Laplacian矩阵广义半正定的队列,参数κi>0即可保证队列性能,且κi越大,收敛速度越快。对于不满足Laplacian矩阵广义半正定的队列,足够大的κi也能保证队列性能。推论2给出了一个实例。
推论2:对任意包含有界不确定性且具有PF通信结构的车辆队列系统(式(3)),如果取κ1≥0.5,κi>0,i=2,3,...,n,那么在控制器ui(i∈χn)的作用下,该队列是严格避撞且紧凑的,同时速度误差是队列稳定的。
证明:对具有PF通信结构的车辆队列:
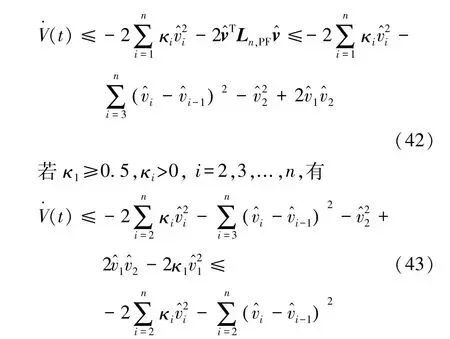
同定理1证明过程的分析,可得推论2。
2.3 修正期望车间距模型
若初始车间距误差不在允许的区间内,由于无法计算车间距势函数,不能直接利用上述方法进行控制。针对大初始车间距误差的情况,提出以下修正期望车间距模型:

代入ηi可得到(0)∈ei,m,ei,M( )。因此,基于修正期望车间距模型,本文提出的控制方法可扩展到大初始车间距误差的工况,理论1对采用修正期望车间距模型的队列仍然成立。
3 仿真验证
通过包含20辆车的数值仿真验证以上理论结果。仿真队列包含两种车型:车辆1,2,4,6,9,10,12,14,17,18为车型一;车辆3,5,7,8,11,13,15,16,19,20为车型二。两种车型的名义参数(包含质量风阻系数和外部阻力)见表1。车辆动力学参数的不确定性设定为正弦或余弦变化形式,例如:对第一辆车ΔM1=100sin(0.02 t),Δc1=0.2sin(0.01 t),ΔF1=100sin(0.01 t)。期望车间距设置为10 m,允许车间距误差区间为(-1 m,1 m)。控制参数设置为:κi=1,εi(0)=1,hi=0.01,i∈χn。首先在小初始误差工况下分析了速度误差一致收敛性以及车间距误差的有界性,接着验证了该算法在大初始误差工况下的适用性。
虚拟头车给定的期望速度曲线方程为


表1 车辆名义动力学参数
3.1 小初始误差工况
所有初始车间距误差在(-1 m,1 m)之间,初始速度误差在(-2 m/s,2 m/s)之间。对PF、BD和BDD 3种通信拓扑的队列都进行了仿真验证。由于篇幅限制,只展示了BD通信拓扑队列部分车辆(2,5,9,13,17,20)的结果,如图2~图4所示。结果表明:本文提出控制器生成的控制力平滑,不存在抖振现象;所有车间距误差保持在允许区间内,保证了队列的避撞性与紧凑性;所有车辆的速度都能稳定跟随给定的期望速度曲线,具有较强的鲁棒稳定性。
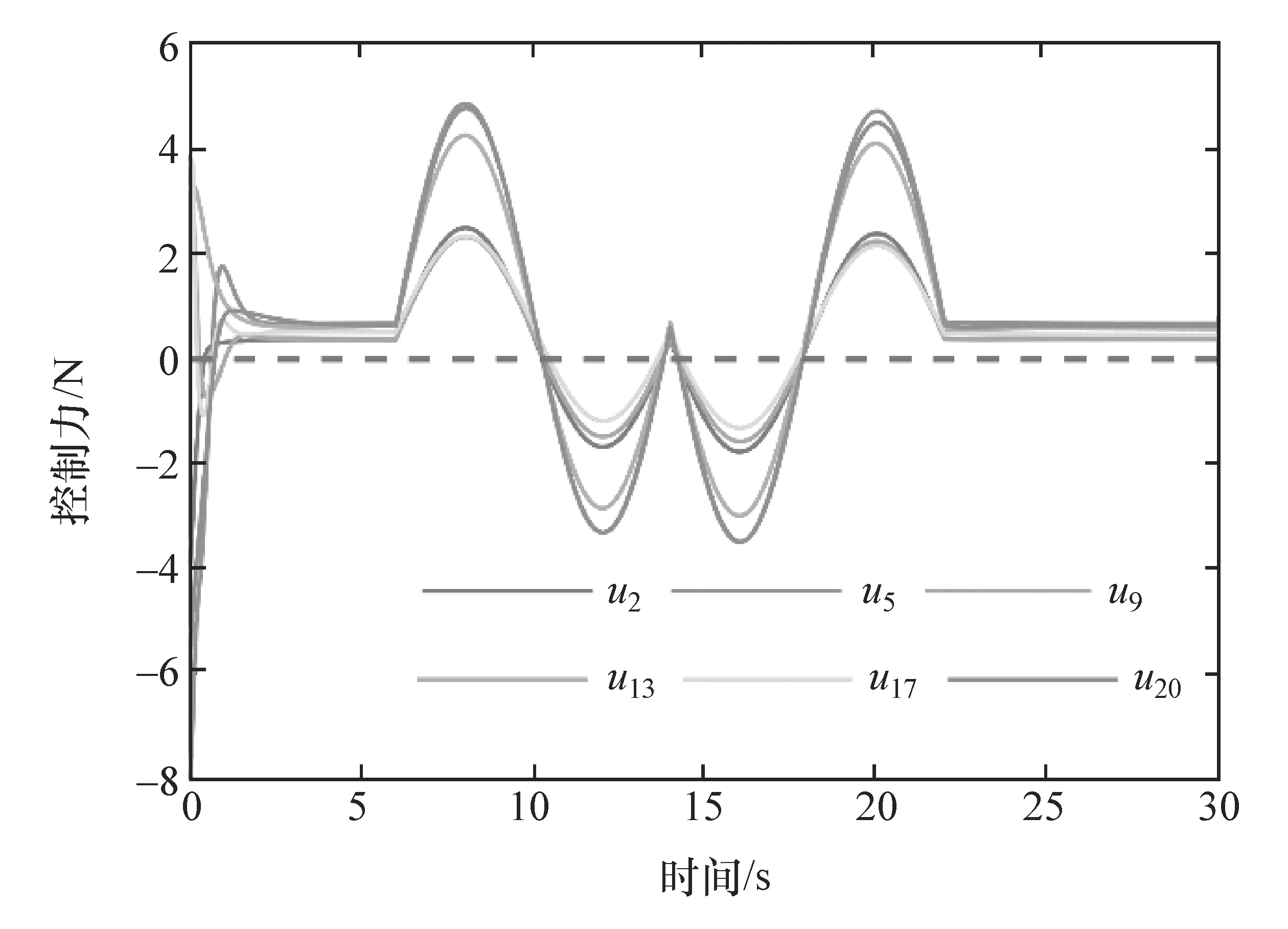
图2 BD通信拓扑队列的控制力-时间图
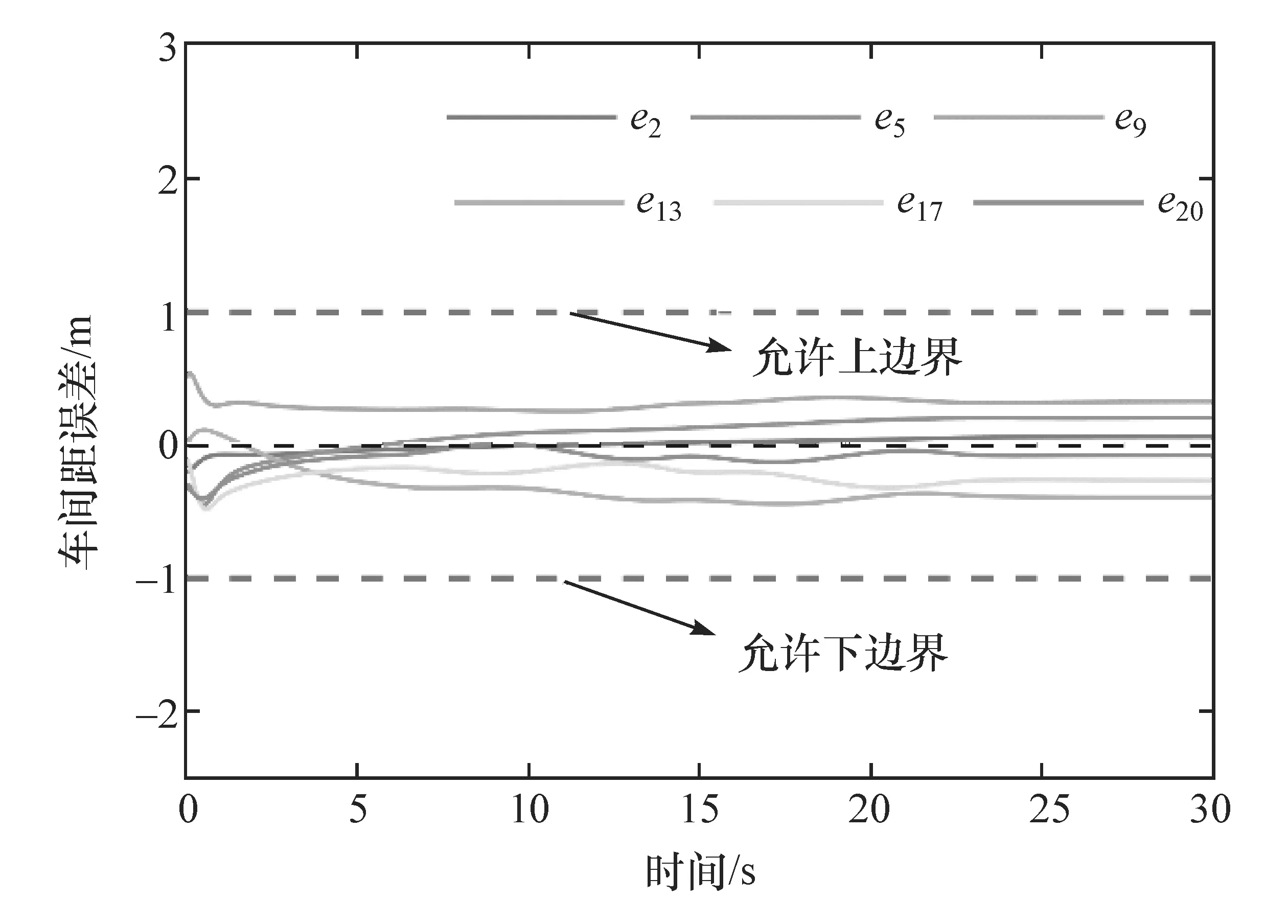
图3 BD通信拓扑队列车间距误差-时间图
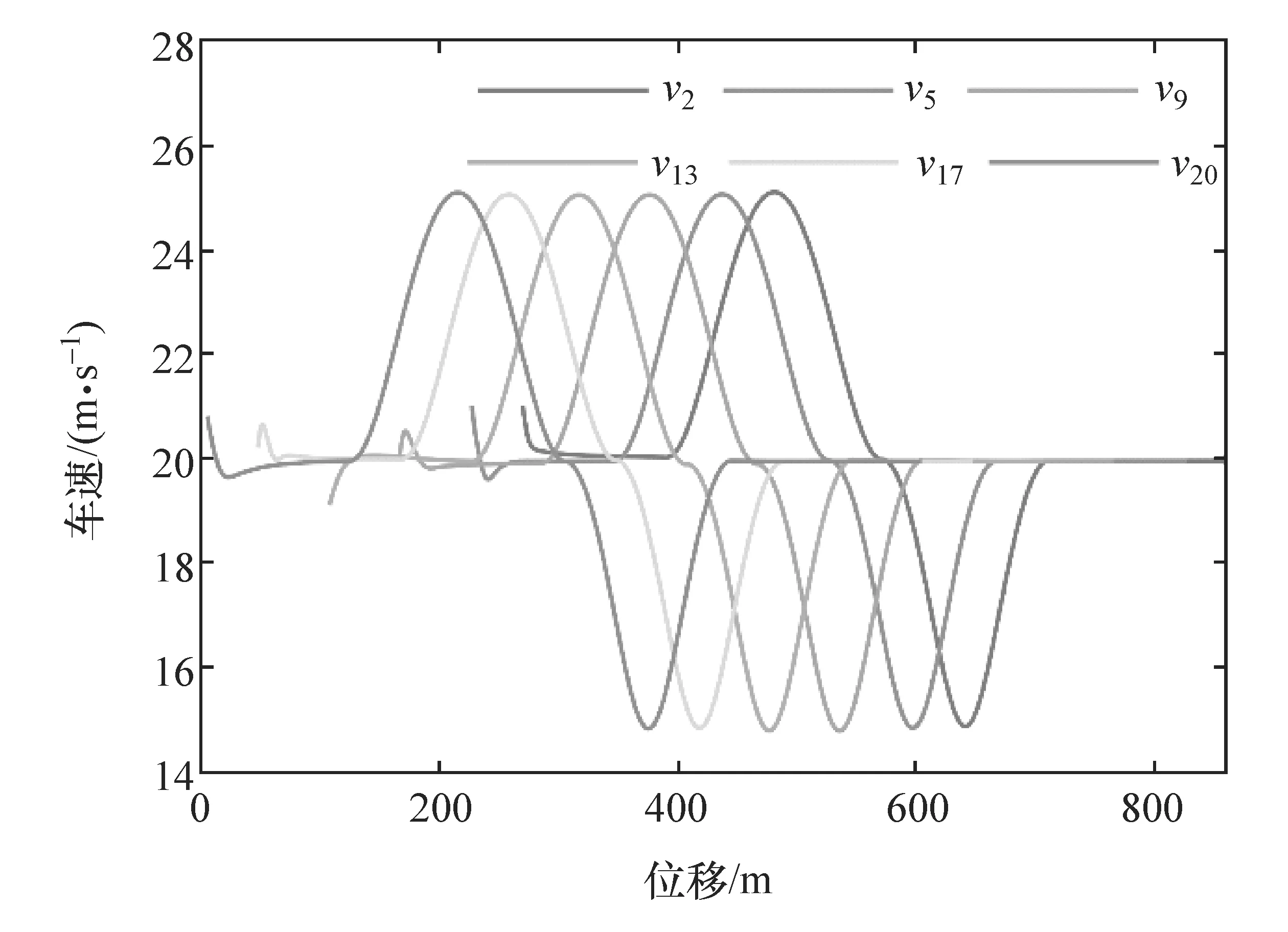
图4 BD通信拓扑队列的速度-位移图
误差的均方根值(RMS)常被用来描述队列的跟随性能[16],其定义为
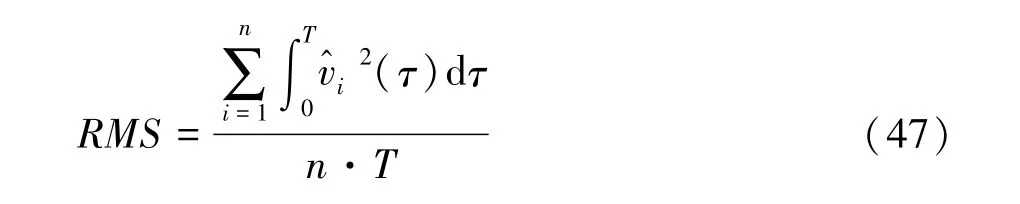
式中T为仿真时长。
表2为不同通信拓扑队列速度跟随误差的RMS值。由于在PF、BD、BDD 3种通信拓扑下,每辆车能获取的邻近车辆信息量依次增多。由表2可以得出一个直观的结论:理想通信条件下,获得邻近车辆信息越多,队列的速度跟随性能越好。

表2 不同通信拓扑队列的速度跟随性能
3.2 大初始误差工况
本文提出的控制算法也适用于存在大初始误差的工况。图5和图6分别为大初始误差工况下队列速度误差和车间距随时间的变化图。如图5所示,即使存在±4 m/s左右的大初始速度误差,在控制器的作用下,所有速度误差都能在6 s内收敛到很小的数值,当期望速度波动时(6~22 s之间),速度误差存在较小波动,当期望速度不变时(22 s以后),速度误差逐渐收敛到0。如图6所示,车间距也能跟随修正期望车间距,同时修正车间距误差严格保持在允许的区间内。即使在大初始误差工况下,本文提出的控制算法也能保证队列避撞性和紧凑性以及速度误差的队列稳定性。
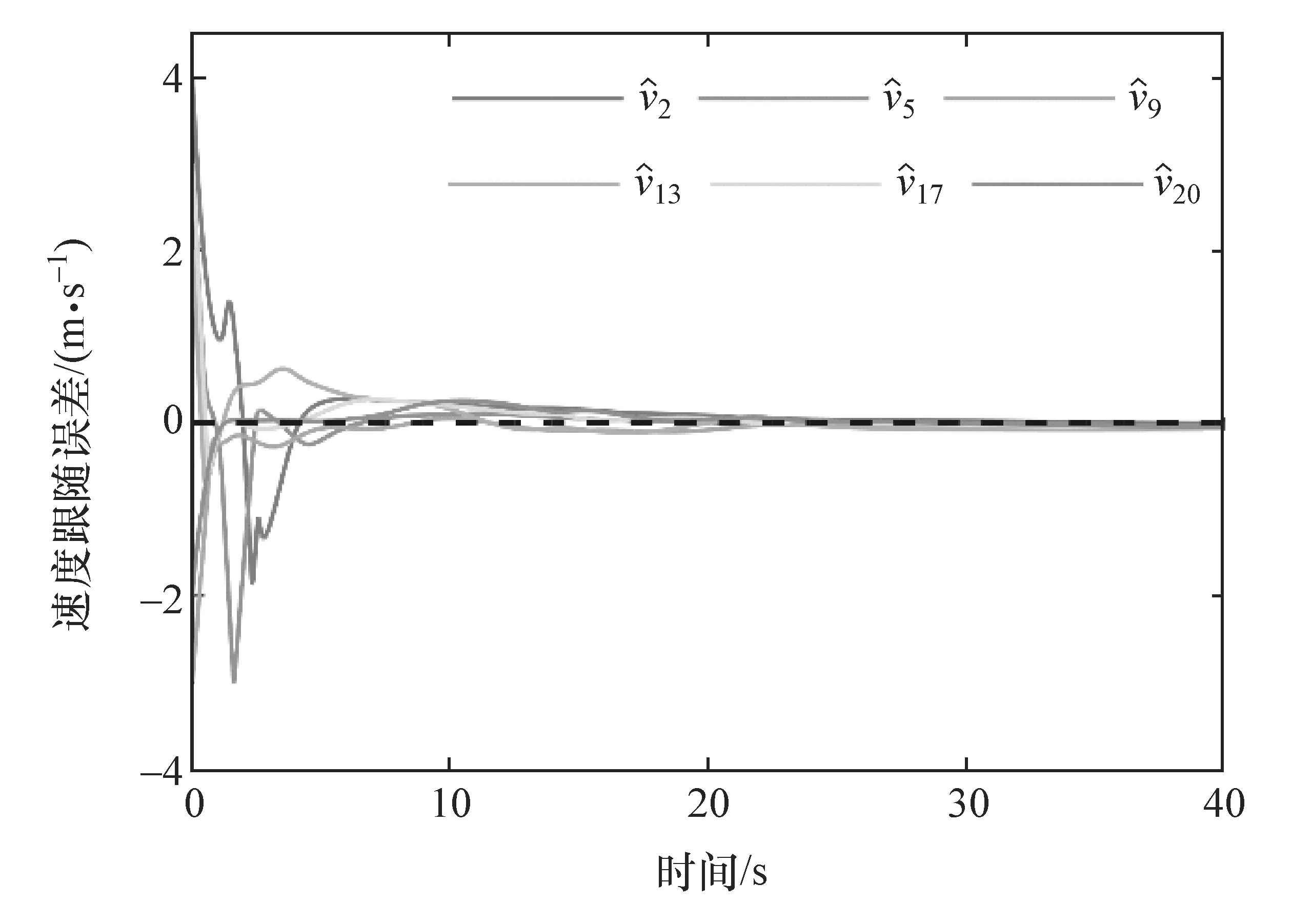
图5 BD通信拓扑队列速度误差-时间图
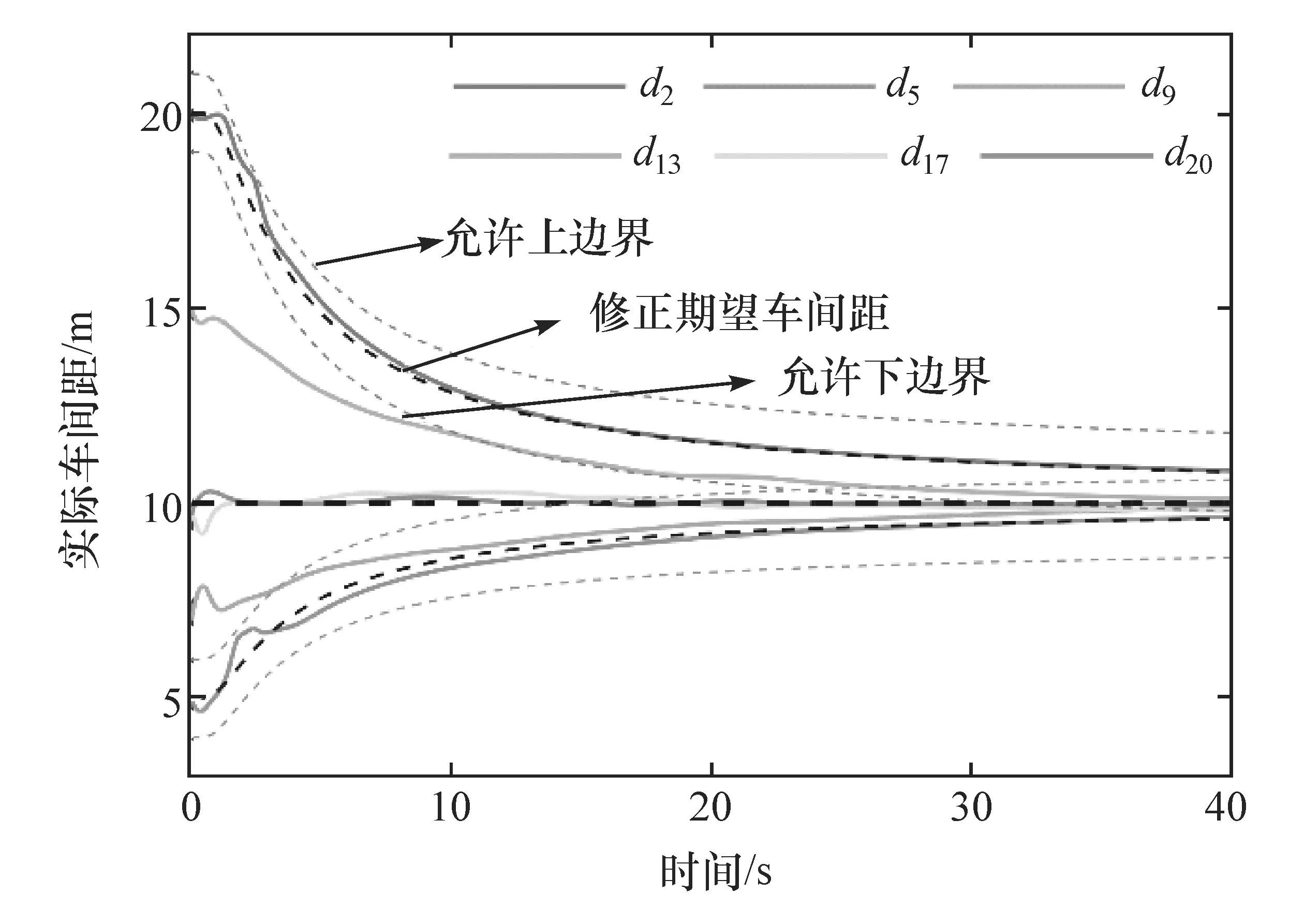
图6 BD通信拓扑队列车间距-时间图
4 结论
设计了智能网联车辆队列纵向分布式鲁棒控制器。理论证明了该控制器能保证队列避撞性与紧凑性以及车速误差的队列稳定性,并分析了通信拓扑和控制参数对控制性能的影响。另外,通过修正期望车间距模型,控制器的应用范围也能扩展到大初始误差工况。仿真结果验证了提出的理论结果。后续研究将聚焦非理想通信条件下严格避撞的队列分布式控制器的设计以及推动实车验证平台的开发。

