裂缝网络支撑剂非均匀分布对开采动态规律的影响

朱维耀，张启涛，岳 明，张燎源

1) 北京科技大学土木与资源工程学院，北京 100083 2) 中国石化胜利油田分公司石油工程技术研究院，东营 257000

水力压裂技术已经广泛应用于非常规油气资源的开发中[1-5]. 在压裂过程中需要注入大量的固体支撑剂颗粒，目的在于防止人造裂缝在闭合压力的作用下完全封闭，从而为地下油气资源的采出提供高导流能力的通道，提升油气田的开发效果[6-7]. 支撑剂的分布状态将直接影响生产井的生产效果，针对直井单裂缝中支撑剂在注入过程后的运移与沉降过程，前人已经进行了较为详细的研究[8-14]. 然而在实际开发过程中，地下的裂缝主要以相互交错的缝网形式存在[15-16]，针对裂缝网络内的支撑剂分布，一些学者进行了物理实验的研究[17-19]，但是相关数值模拟及理论研究相对缺乏. 同时，目前支撑剂的研究仍然主要集中在支撑剂的运移过程上，针对支撑剂分布状态对生产动态规律影响的模拟研究相对较少，相关问题具有较大的研究价值.

为了准确地模拟支撑剂在裂缝的运移分布规律以及铺砂过程结束后裂缝在实际储层中的生产表现，本文在之前已经建立的裂缝铺砂数学模型[12]、裂缝导流能力数学模型[20]及含启动压力梯度致密储层开发数学模型[21]的基础上，建立了致密油压裂开发全耦合计算模型，研究支撑剂在裂缝网络的分布状态对致密储层开采动态规律的影响，以期为现场开发提供指导.

1 数学模型选择

1.1 裂缝网络携砂液流动数学模型

携砂液主要由固体支撑剂和压裂液组成，因此裂缝中的携砂液流动是一种典型的固液两相流问题. 采用混合物模型对携砂液流动进行模拟计算. 混合物模型是一种简化的两相模型，只求解一组动量方程，即混合物的连续性方程和固相输运方程，具有较高的计算效率和收敛性，适合裂缝等复杂几何的模拟计算[22-24]. 本次模拟不考虑温度对两相流动的影响.

模型动量方程可以表示为[12]：

其中，u是混合物的质量平均速度，m·s-1；p是压力，Pa；g是重力加速度，m·s-2；cs是颗粒质量分数；uslip是固相和液相间的相对速度，m·s-1；ρ是混合物的密度，kg·m-3，表示为：

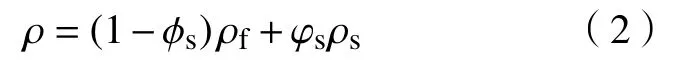
其中，ρf和ρs分别是纯液体和固体的密度，kg·m-3；φs是固相的体积分数. 根据Krieger表达式[25]，混合物黏度η表示为：

其中，ηf是纯液体的动力黏度，Pa·s；φmax是最大的颗粒浓度.

混合物模型中的连续性方程为[12]：

固相的输运方程为[12]：

其中，us是固相速度，m·s-1，它可以表示为[12]：

将式（6）代入式（5）中[12]：

基于以上方程，使用COMSOL多物理场模拟软件对携砂液流动进行模拟.

1.2 裂缝网络几何参数和致密储油层开发数学模型

铺砂过程结束后，裂缝宽度和裂缝渗透率都会因受压发生改变. 朱维耀等[20]根据支撑剂的最密排列以及Carman-Kozeny公式，结合弹性力学的相关知识，建立了考虑铺砂浓度、闭合压力、支撑剂粒径、支撑剂材料以及支撑剂嵌入的裂缝渗透率与缝宽（即导流能力）计算模型. 通过该模型，铺砂计算出的支撑剂颗粒浓度可以转换为此时的裂缝宽度和渗透率，进而可以用于之后的致密储层黑油模型计算中.

受压后的裂缝宽度计算公式如下[20]：

其中，wfh为受压后裂缝的宽度，m；r为支撑剂直径，m；C为铺砂浓度，由上文计算出的支撑剂颗粒浓度换算得到，kg·m-2；mo为单个支撑剂质量，kg；h1为支撑剂嵌入裂缝内的距离，m，其计算公式如下[20]：

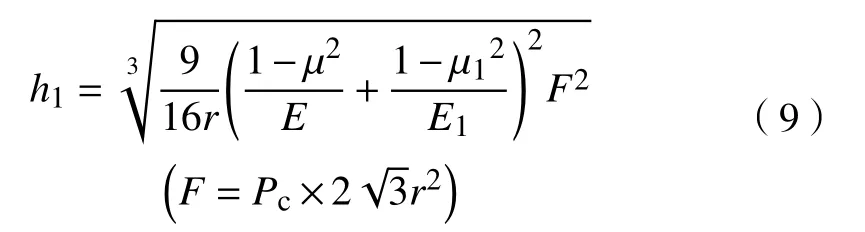
其中，F为一个支撑剂所受的压力，N；pc为闭合压力，Pa；μ为支撑剂的弹性模量，Pa；E为支撑剂的泊松比；μ1为壁面材料的弹性模量，Pa；E1为壁面材料的泊松比.

式（8）中的Bt为破碎率，与支撑剂材料及闭合压力大小有关：

其中，pm为支撑剂开始发生破裂的临界闭合压力，Pa；a和b分别为实验拟合系数，量纲为一.

裂缝渗透率计算公式如下[20]：

其中，no为单位面积支撑剂的个数；τ为迂曲度.

获得缝网裂缝宽度和渗透率之后，需要置入储层模型中进行模拟生产，从而评价压裂改造效果，获得生产动态规律. 选取含启动压力梯度致密油储层进行模拟. 针对含启动压力梯度的致密油储层开发模拟，朱维耀等[21]提出了体积力近似法，可以较为准确地对含启动压力梯度储层流体流动进行计算模拟. 本文模型假设储层中的流体只能先流入裂缝，之后才能通过裂缝流入井筒.

基于以上方程，使用COMSOL多物理场模拟软件及Livelink for MATLAB研究裂缝网络支撑剂非均匀分布对致密储层开采动态规律的影响.

2 裂缝网络支撑剂运移分布模拟

2.1 裂缝网络几何建模与参数选取

基于Warren-Root正交裂缝网络模型[26]以及Mayerhofer等[27]的缝网模型，进行了裂缝网络几何建模（图1）. 裂缝网络由两条人工主裂缝和两条横向次级裂缝组成，主裂缝与次级裂缝长度均为100 m，主裂缝初始缝宽为0.02 m，次级裂缝初始缝宽为0.005 m，井筒半径为0.1 m. 携砂液由井筒首先流入主裂缝后再流入次级裂缝.

图1 裂缝网络几何模型示意图Fig.1 Illustration of fracture network model

为了简化几何模型，同时减少模型计算量，在实际计算时对裂缝网络模型进行了对称简化处理（图2）. 编号1、2和3为携砂液出口，设置为压力出口边界且无固体通量；4、5和6a为对称边界；6b为入口，设置为速度入口边界.

图2 裂缝网络对称简化示意图Fig.2 Symmetric fracture network model

对上述几何模型进行网格划分，使用有限元法进行求解. 为了更精确地捕捉固相参数，在靠近入口和下边界处进行网格加密处理. 计算中使用的基本参数如表1中所示.

表1 基本计算参数Table 1 Basic calculation parameters

2.2 裂缝网络铺砂计算结果分析

（1）裂缝网络支撑剂运移与分布状态规律.

根据上述模型与计算参数，首先对裂缝网络内的携砂液流动进行模拟，计算时间为1000 s，计算结果如图3所示.

图3 裂缝网络铺砂过程示意图Fig.3 Illustration of proppant-laden fluid injection process

从图3中可以看出，裂缝网络中支撑剂浓度的分布状态要明显不同于单裂缝. 支撑剂在进入裂缝网络之后逐渐以“砂包”状缓慢向前推进，在到达主裂缝与分支缝交汇点后，逐渐形成支撑剂堆积，裂缝交汇点处的支撑剂沉降堆积高度要明显高于其他部分. 继续注入携砂液，支撑剂开始进入次级裂缝，从图3（c）中可以看出，铺砂过程结束后次级裂缝外侧部分的砂堤堆积高度要比主裂缝中小25%～50%，其支撑剂悬浮区则明显更大. 相比较而言，次级裂缝内侧部分由于沟通了两条主裂缝，其支撑剂堆积高度也要明显高于外侧部分，改造效果更加明显.

（2）铺砂参数对裂缝网络平均导流能力影响.

为了研究支撑剂物性参数以及铺砂施工参数对铺砂效果的影响，选取不同支撑剂粒径、材料和携砂液注入速度进行铺砂模拟. 通过模拟得到缝网各处的支撑剂浓度后，通过式（8）和式（11）计算缝网内各部分导流能力，再对缝网进行整体积分，取得裂缝网络的平均导流能力，并将该导流能力参数作为衡量铺砂效果进行参数优选的定量指标.

为了研究支撑剂粒径对裂缝网络整体导流能力的影响，选取直径为200、300和400 μm的支撑剂颗粒进行计算，在其他因素相同的情况下，研究不同闭合压力下，不同粒径支撑剂所形成裂缝平均导流能力. 计算结果如图4所示，缝网平均导流能力与支撑剂粒径大小呈正相关关系：在闭合压力为10 MPa的条件下，粒径400 μm计算出的导流能力要比200 μm情况大10 D·cm左右；当闭合压力压力增大到60 MPa时，二者则相差3 D·cm. 整体而言，大粒径支撑剂的对裂缝导流能力的正作用较为明显.

图4 支撑剂粒径对缝网整体导流能力的影响Fig.4 Effect of proppant diameter on fracture network conductivity

为了研究支撑剂材料对裂缝网络整体导流能力的影响，选取石英和陶粒作为模拟对象. 陶粒弹性模量为100 GPa，泊松比为0.25；石英弹性模量为30 GPa，泊松比为0.15. 计算结果如图5所示，在相同铺砂条件下，石英支撑剂计算出的缝网平均导流能力要小于陶粒. 二者之间的差异大小与闭合压力呈正相关关系. 当闭合压力为0时，二者的导流能力基本相等，而当闭合压力上升到60 MPa时，石英的破碎率远高于陶粒，其导流能力要比陶粒小50%. 因此，在实际选取支撑剂种类时，支撑剂的材料也是必须要考虑的因素. 变形能力小，材料强度大，不易破碎的材料对于水力压裂改造效果具有较大的正影响.

图5 支撑剂材料对缝网整体导流能力的影响Fig.5 Effect of proppant materials on fracture network conductivity

为了研究携砂液注入速度对裂缝网络整体导流能力的影响，选取携砂液的法向入口流速分别为0.3，0.4，0.5和0.6 m·s-1，计算裂缝网络平均导流能力，计算结果如图6所示.

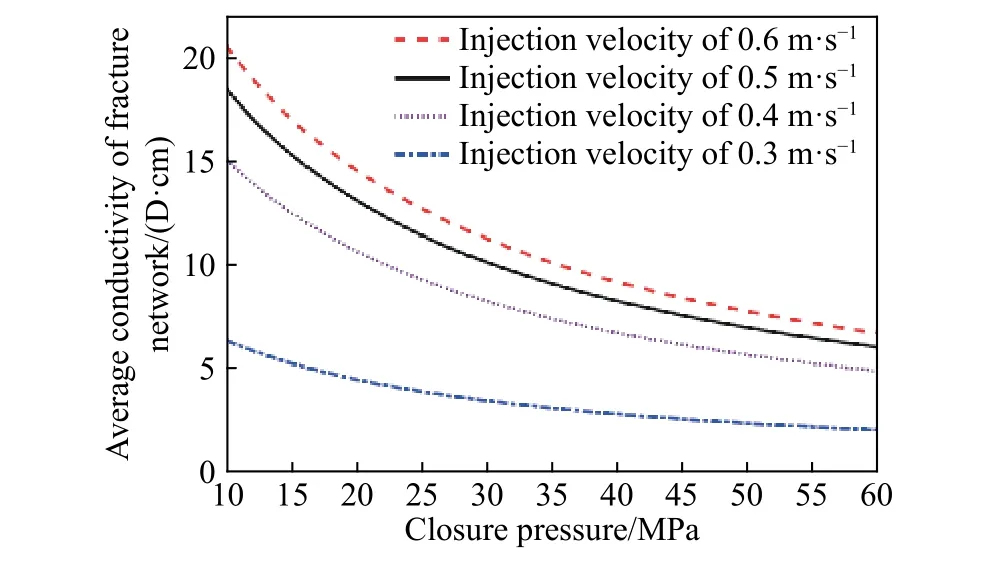
图6 携砂液注入速度对缝网整体导流能力的影响Fig.6 Effect of proppant-laden fluid injection velocity on fracture network conductivity

从图6可以发现，注入携砂液速度越大，其裂缝网络的整体导流能力越大，二者呈现正相关关系. 但是随着流入速度逐渐增加，裂缝网络整体导流能力的增长逐渐变缓，当注入速度大于0.6 m·s-1，时，再继续增加注入速度，导流能力增长比较有限. 通过计算注入砂量大小以及裂缝平均导流能力的比值，最佳的携砂液注入速度为0.4 m·s-1左右.

3 裂缝网络支撑剂非均匀分布对致密储层开采动态规律影响

传统油藏数值模拟模型一般假定压裂裂缝内部渗透率相等，缝宽相等. 而实际情况下，由于支撑剂在裂缝中的运移分布差异，裂缝各处的渗透率与缝宽存在差异，这种差异往往会导致计算误差，影响模拟计算及结果的准确性. 通过对比支撑剂理想分布条件和支撑剂非均匀分布条件下的致密储层生产表现，定量研究支撑剂非均匀分布对油藏数值模拟计算结果的影响，模型计算参数如表2所示.

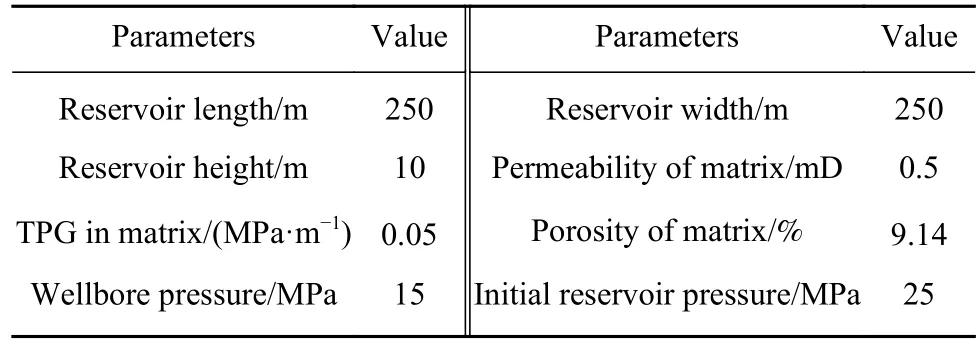
表 2 基本计算参数Table 2 Basic calculation parameters

图7 裂缝网络内支撑剂理想均匀分布与不均匀分布条件下的致密储层开发300 d压力场对比. （a）支撑剂均匀分布状态；（b）基于支撑剂均匀分布的储层压力场分布；（c）支撑剂不均匀分布；（d）基于支撑剂不均匀分布的储层压力场分布Fig.7 Comparison between pressure distribution based on proppant idealized and uneven distribution at 300 days in a tight oil reservoir: (a) idealized proppant distribution; (b) pressure distribution with even proppant distribution; (c) uneven proppant distribution; (d) pressure distribution with uneven proppant distribution

支撑剂理想均匀分布如图7（a）所示，支撑剂非均匀分布如图7（c）所示. 两种分布状态衍生计算出的致密油储层生产300 d后压力场分布分别如图7（b）和图7（d）所示. 可以看出考虑支撑剂非均匀分布的条件下，裂缝网络的有效控制面积相对较小，压降主要集中在主裂缝周边；而支撑剂理想分布的条件下，裂缝网络的有效控制面积更大，压力波及范围更广，压降集中在主裂缝以及次级缝周边. 因此在油藏数值模拟的过程中，将所有裂缝都假定为理想等宽裂缝的做法并不合理，需要针对储层特性以及压裂施工方式进行具体分析.

研究同时发现，基质渗透率大小会对考虑与不考虑支撑剂不均匀分布两种情况之间的产量差异产生影响. 在其他参数相同的条件下，改变储层的基质渗透率，计算两种情况下的产量增长系数[27]进行对比，计算结果如图8所示.

图8 基质渗透率对计算产量差异的影响Fig.8 Effect of matrix permeability on difference in calculated productivity

从图8中可以看出，两种情况下的产量差异与基质渗透率呈反比关系，该结论与Kong等[28]的计算结果基本一致. 当模型基质渗透率为0.05 mD时，支撑剂理想均匀分布条件下的产量要比考虑支撑剂不均匀分布的情况高41.7%，在这种情况下不能忽略支撑剂非均匀分布的影响. 而当基质渗透率为5 mD时，二者的产量差异在5%以内，此时如果用理想化等宽等渗裂缝进行油藏数值模拟则较为合理.

4 实例应用

以胜利油田某低渗透区块一水平井为例，完钻井深为3542 m，油层厚度为20 m. 根据压裂层测井解释情况，平均渗透率为5.8 mD，地面原油平均密度为0.858 g·cm-3，平均原油黏度为16.68 mPa·s，水平井压裂14段，平均段间距为67.2 m，平均裂缝半长为152.1 m. 依照现场提供模拟参数，首先对目标储层进行铺砂模拟，而后转为生产模拟，计算产量与实际油田产量如图9所示.

从对比图中可以看出，铺砂-生产耦合模拟计算得出的产量曲线与实际水平井产量曲线较为贴合，验证了模型的准确性，同时为模型今后进一步应用与实际生产奠定了基础. 该模型具有较大的应用与拓展空间.

图9 耦合计算模型结果与实际生产数据对比Fig.9 Comparison of oil rate between coupling model and oil field data

5 结论

为了研究裂缝网络内支撑剂运移分布规律以及支撑剂不均匀分布对致密储层的影响，基于作者提出的多个数学模型，构建了致密储层水力压裂生产耦合计算模型，对致密油储层压裂开发生产全过程进行模拟，得到了以下几点结论：

（1）水平井裂缝网络中的支撑剂运移与分布状态与垂直井单裂缝存在明显差异. 在裂缝网络中，支撑剂会在裂缝交汇处产生堆积，堆积高度高于缝网其他部分. 次级裂缝中的支撑剂更多的处于悬浮状态，且支撑剂堆积高度相较于主裂缝小25%～50%. 沟通次级缝具有更高的支撑剂沉降堆积程度，有利于油气资源的开发.

（2）裂缝网络平均导流能力与支撑剂粒径大小呈正比. 缝网导流能力还与法向注入速度呈正比，考虑注砂经济性，该模型条件下最佳的携砂液注入速度为0.4 mμs-1左右.

（3）在进行油藏数值模拟时应考虑支撑剂非均匀分布对计算结果的潜在影响. 计算结果显示，当基质渗透率为0.05 mD时，支撑剂理想均匀分布条件下计算出的产量要比考虑支撑剂非均匀分布的情况高41.7%；当基质渗透率逐渐增大到5 mD时，产量差异在5%以内，此时忽略支撑剂非均匀分布相对合理.