分层胶结充填体力学特性及裂纹演化规律

唐亚男，付建新✉，宋卫东，张永芳

1) 北京科技大学土木与资源工程学院，北京 100083 2) 北京科技大学金属矿山高效开采与安全教育部重点实验室，北京 100083

充填采矿法不仅能有效控制采空区塌陷，而且能合理处置选矿废弃尾砂，因而被广泛应用于金属非金属矿山[1-2]. 胶结充填体作为采场的重要组成部分，对维持采空区安全稳定、防止地表构筑物塌陷等方面发挥着不可替代的作用. 因而研究荷载作用下胶结充填体力学特性与内部裂纹演化规律具有重要意义.

尾砂胶结充填体是一种由胶结剂、尾砂和水泥混合而成的多相复合材料，其强度通常介于土与岩石之间，国内外研究学者对于其流动特性、力学特性、微观结构特性及宏观破坏模式的研究相对较多，在充填体力学领域取得了丰硕的成果[3-4].徐文彬等[5-6]借助TIR红外监测系统及电阻率测量系统对充填体单轴压缩下的应力-应变行为、电阻率变化规律及红外热力学特性进行了深入研究. 程爱平等[7-8]针对不同尺寸胶结充填体，开展单轴压缩试验同时全程监测胶结充填体声发射信号，重点研究了胶结充填体损伤演化尺寸效应及破裂纹时空演化规律，同时对充填体破裂行为进行了有效预测. 李长洪等[9-10]基于能量守恒理论，探索胶结充填体与矿石合理匹配关系，同时发现胶结充填体强度具有空间差异性. 宋卫东等[11-12]模拟井下开挖及爆破等动载行为，开展胶结充填体循环冲击试验，研究了胶结充填体的动载力学行为及破坏特征.

以上研究主要聚焦结构完整的充填体，而对于采用阶段嗣后充填的矿山，采场往往划分为矿房和矿柱，一步回采矿房，胶结充填完毕，二步回采矿柱. 由于阶段高度较大（达40 m），如果全阶段采用高灰砂比尾砂胶结充填，将会大大增加充填成本，若全阶段采用低灰砂比尾砂胶结充填，虽可大大节约成本，但当二步矿柱开挖，胶结充填体出现单侧或双侧揭露，由于强度不足，可能导致充填体出现垮落，这样不仅增大安全风险而且还会导致混入贫化. 而分层充填可很好地解决这一问题，即底部和顶板采用高灰砂比尾砂胶结充填，而中间部位采用低灰砂比尾砂胶结充填，这样不仅可保持充填体自立安全稳定，还能节约充填成本. 然而，分层充填易导致充填体出现分层等结构特性，结构特征的出现会导致充填体力学性能出现一定程度劣化. Cao等[13-17]重点考虑结构面数量、结构面角度等因素，认为充填体力学特征与结构面状态密切相关. Xu等[18]建立了结构面数量与单轴抗压强度之间的定量函数关系. WANG等[19-20]基于不同试验参数，构建了结构面与荷载耦合作用下的损伤本构模型，同时对分层充填体能量演化规律进行了深入分析. Zhang等[19]基于霍普金森压杆试验，研究了不同应变速率对分层充填体动态力学特性及破坏模式的影响. 基于以上研究，结构特性对胶结充填体力学特征、能量演化规律及破坏模式具有重大影响，而由于采矿方法或充填能力的影响，胶结充填体出现分层等结构现象不可避免，因而研究和分析结构型充填体力学特性、掌握其内部破裂机理对矿山生产意义重大.

在其他学者的研究基础之上[20-25]，本文聚焦于分层胶结充填体(本文定义分层充填体[20]为高灰砂比与低灰砂比充填体组合体）试件，通过制作高度比（中间层高度与试件高度的比值）为0.2、0.4、0.6和0.8，灰砂比（指中间层灰砂比）为1∶4、1∶6、1∶8和1∶10的16组充填体试件，开展单轴压缩试验，探讨其力学特性. 同时基于二维颗粒流软件（PFC-2D）模拟分层充填体单轴压缩过程，分析其内部裂纹演化机理.

1 分层胶结充填体力学特性实验研究

1.1 试验材料

本次试验尾砂来自于山东省某金矿，采用SA-CP3粒径分析仪对烘干过后的尾砂样品进行粒径测试，得到尾砂粒径分布曲线如图1所示. 分析图1发现，粒径小于129.48 μm的细颗粒体积占比超过50%，平均粒径为144.26 μm. 尾砂密度和质量比表面积分别为2.65 g·m-3和92.37 m2·kg-1.

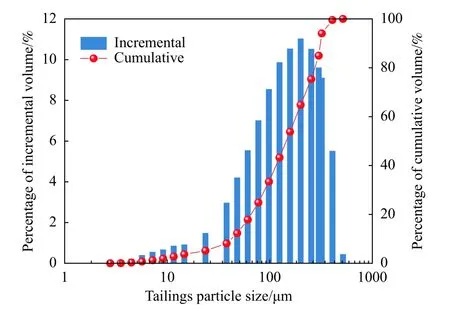
图1 尾砂粒径分布曲线Fig.1 Distribution curve of tailings particle size

利用X射线衍射仪对试验尾砂化学成分进行分析，结果如表1所示. 尾砂主要矿物成分为SiO2和Al2O3，质量分数分别为65.7%和14.3%. 这些主要成分（SiO2、Al2O3、CaO等）通常有利于充填体凝聚力和强度的增加.

矿山采用42.5R普通硅酸盐水泥作为胶结剂，试验用水泥的化学成分如表1所示. 该金矿采用当地自来水作为混合水来源进行充填料浆制备，由于实验在北京科技大学实验室完成，采用矿山当地自来水进行试验研究非常不方便，且自来水成分差别不大，成分的差异对充填体力学性质的影响可忽略不计，因此本次实验采用实验室自来水.

1.2 分层充填体试件制作及单轴压缩试验

为研究分层充填体中间层高度比（以下简称高度比）和中间层灰砂比对其力学特性的影响规律，保持顶层和底层灰砂比为1∶4不变，设置中间层灰砂比为1∶4、1∶6、1∶8和1∶10、中间层高度比为0.2、0.4、0.6和0.8，本次实验采用了小模具进行实验研究，模具内径为50 mm，高度为100 mm.养护龄期为58 d，采用恒温恒湿养护箱进行养护，温度为20±5 ℃、相对湿度为95%±5%.

分层充填体制作过程（图2）为：（1）混合搅拌：首先将水泥、尾砂和水按设定比例混合，然后将混合料浆放在搅拌机下搅拌均匀备用；（2）模具充填：首先按设定高度充填底层料浆，间隔24 h后按设定高度充填中间层料浆，再间隔24 h充填顶层料浆至100 mm高度；（3）脱模养护：将充填完成的试件放入养护箱，养护3 d后拿出脱模继续养护至58 d备用. 单轴压缩试验是获得充填体试件力学参数的最直接方式. 利用GAW-2000微机控制电液伺服压力机对不同分层充填体试件开展单轴压缩试验. 采用位移控制方式进行加载，速率为0.5 mm·min-1，电脑会自动记录加载过程中应力-应变曲线，最后以Excel格式输出. GAW-2000试验系统如图2所示.

2 试验结果及分析

2.1 分层充填体试件单轴抗压强度

单轴抗压强度被认为是充填体最重要的力学参数之一，而充填体灰砂比及高度比均对其单轴抗压强度（UCS）有很大影响. 因此本文试验设置两个变量，分别为灰砂比和高度比，每个变量设置4个水平，共16组分层充填体试件，每组试件制作3个，共48个试件.

表1 尾砂和水泥化学成分（质量分数）Table 1 Chemical composition of tailings and cement (mass fraction)%

图2 分层充填体试件制作与单轴压缩试验Fig.2 Making and uniaxial compression test of layered backfill specimens

2.1.1 高度比的影响

为分析分层充填体高度比对其单轴抗压强度的影响规律，以高度比为横坐标、单轴抗压强度为纵坐标，得到高度比与单轴抗压强度关系，如图3所示.

由图3可知，分层充填体单轴抗压强度随高度比增加而降低. 以灰砂比为1∶4进行说明，当分层充填体试件高度比为0.2时，其单轴抗压强度为6.15 MPa，当高度比从0.2增加到0.4时，对应的单轴抗压强度为5.98 MPa，强度降低约2.8%，高度比继续增加至0.6时，其单轴抗压强度降低至5.95 MPa，当高度比增加至0.8时，此时分层充填体单轴抗压强度为5.57 MPa，对比高度比为0.6时降幅约6.4%，对比高度比为0.2时降幅达9.4%.

分别采用线性函数、指数函数及多项式函数对分层充填体单轴抗压强度与高度比之间的关系进行拟合，拟合复相关系数（R2）如表2所示.

表2结果显示，当灰砂比分别为1∶4、1∶6、1∶8和1∶10时，指数函数拟合复相关系数（R2）分别为0.892、0.968、0.996和0.953，平均值达0.952. 线性函数和多项式函数拟合复相关系数（R2）均明显低于指数函数，其平均值分别为0.845和0.882. 因此认为分层充填体高度比与其单轴抗压强度之间存在较好的指数函数关系，其表达式为：

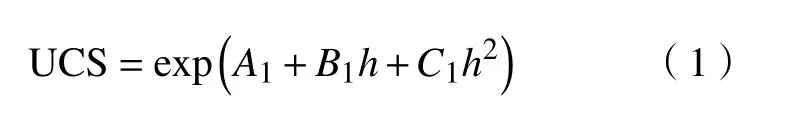
其中，UCS为分层充填体单轴抗压强度，MPa；h为分层充填体中间层高度比；A1、B1和C1表示与高度比及灰砂比有关的参数.

2.1.2 灰砂比的影响

充填体灰砂比对单轴抗压强度有重要影响.图4所示为分层充填体单轴抗压强度与灰砂比关系曲线.

观察图4发现，分层充填体单轴抗压强度随灰砂比增大而增大. 当灰砂比为1∶4时，高度比为0.2的试件单轴抗压强度为6.15 MPa，高度比为0.4、0.6和0.8的试件单轴抗压强度分别为5.98、5.95和5.57 MPa；当灰砂比减小为1∶6时，对应的单轴抗压强度分别为5.23、5.14、5.13和4.94 MPa，较灰砂比为1∶4时的试件单轴抗压强度分别降低15.0%、14.0%、13.8%和11.3%；灰砂比减小为1∶8时，单轴抗压强度分别减小至4.81、4.72、4.66和4.65 MPa，较灰砂比为1∶6时减小幅度分别为8.0%、8.2%、9.2%和5.9%；当灰砂比减小到1∶10时，对应的单轴抗压强度分别降低至4.64、4.37、4.30和3.95 MPa，对比灰砂比为1∶8时对应的单轴抗压强度，降幅分别为3.5%、7.4%、7.7%和15.1%.

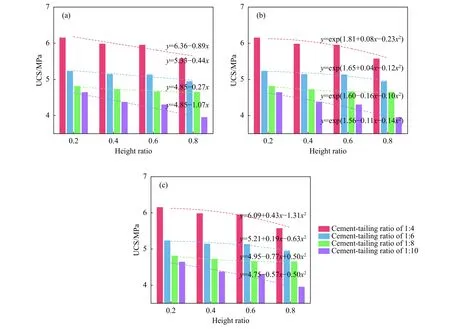
图3 高度比与单轴抗压强度关系. （a）线性拟合；（b）指数拟合；（c）多项式拟合Fig.3 Relationship between height ratio and uniaxial compressive strength: (a) linear fitting; (b) exponential fitting; (c) polynomial fitting

表 2 拟合复相关系数(R2)Table 2 Fitting complex correlation coefficient (R2)

借助线性函数、指数函数及多项式函数对分层充填体单轴抗压强度与灰砂比之间的内在关系进行拟合，各拟合复相关系数 （R2）见表3所示.

分析表4得到，线性函数和指数函数均能较好地表征分层充填体单轴抗压强度与灰砂比之间的关系，其复相关系数（R2）平均值分别高达0.947和0.955，最高可达0.968和0.977. 对比三种拟合函数，多项式函数拟合相关性最高，当高度比分别为0.2、0.4、0.6和0.8时，其复相关系数（R2）分别为0.993、0.987、0.994和0.938，复相关系数（R2）平均值高达0.978，最高可达0.994. 因此综合分析认为，多项式函数能最好地表征分层充填体单轴抗压强度与灰砂比之间的关系，其表达式可表示为：

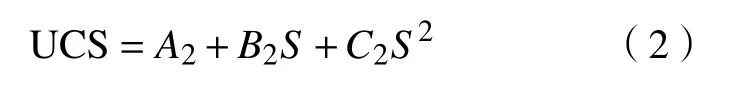
式中：S表示灰砂比；A2、B2和C2表示与灰砂比及高度比有关的参数.

2.2 分层充填体弹性模量

2.2.1 高度比的影响

为研究分层充填体弹性模量与其高度比之间的内在联系，以弹性模量E为纵坐标、高度比为横坐标，得到弹性模量与高度比关系曲线，如图5所示.

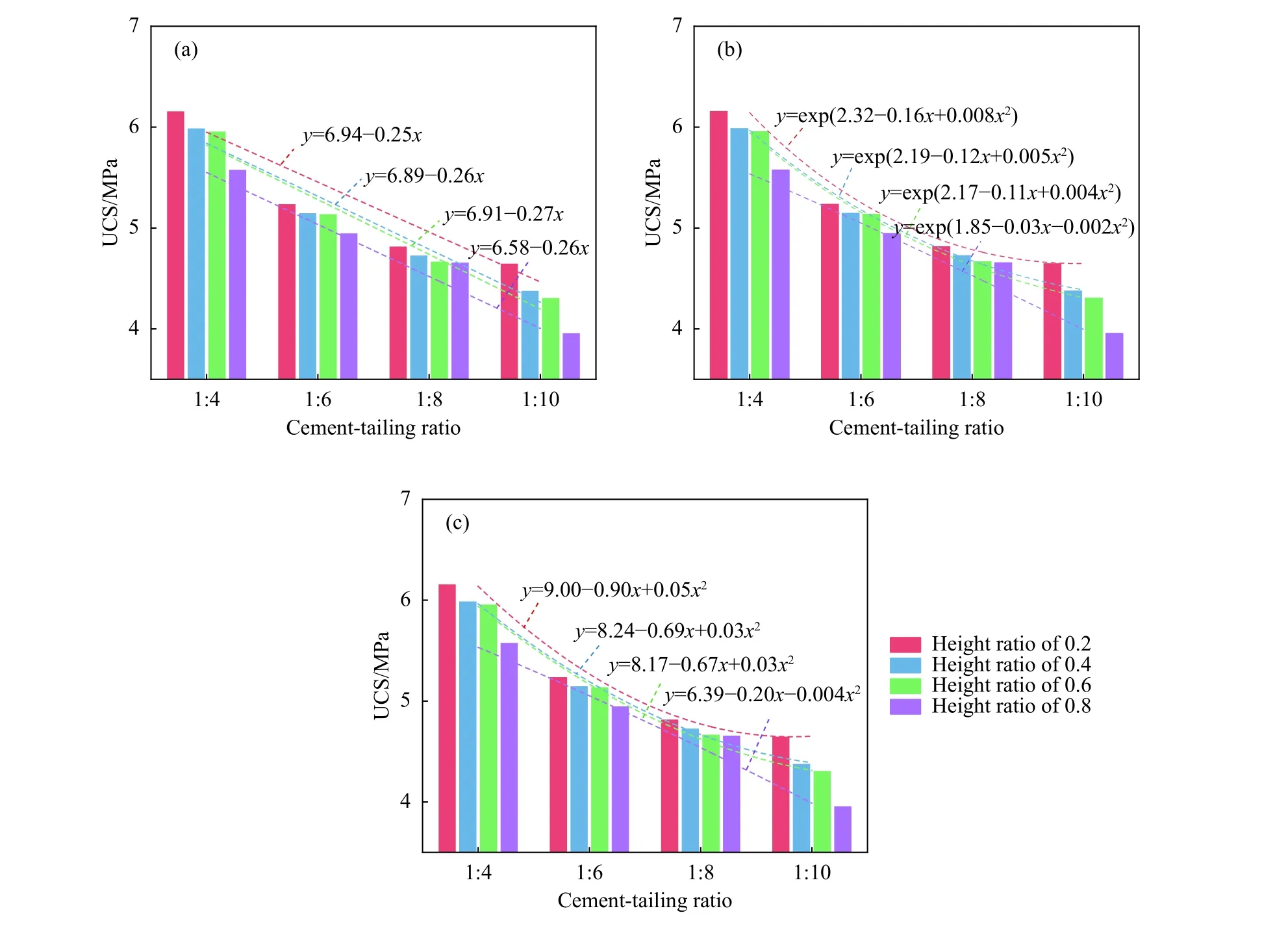
图4 灰砂比与单轴抗压强度关系. （a）线性拟合；（b）指数拟合；（c）多项式拟合Fig.4 Relationship between cement-tailing ratio and uniaxial compressive strength: (a) linear fitting; (b) exponential fitting; (c) polynomial fitting

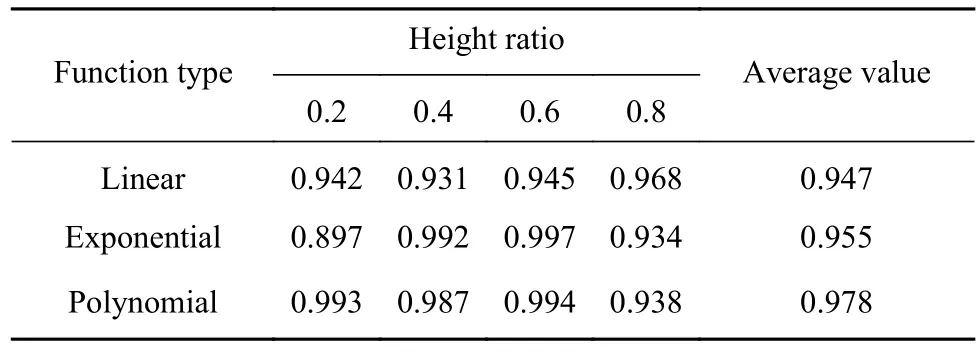
表 3 拟合复相关系数(R2)Table 3 Fitting complex correlation coefficient (R2)

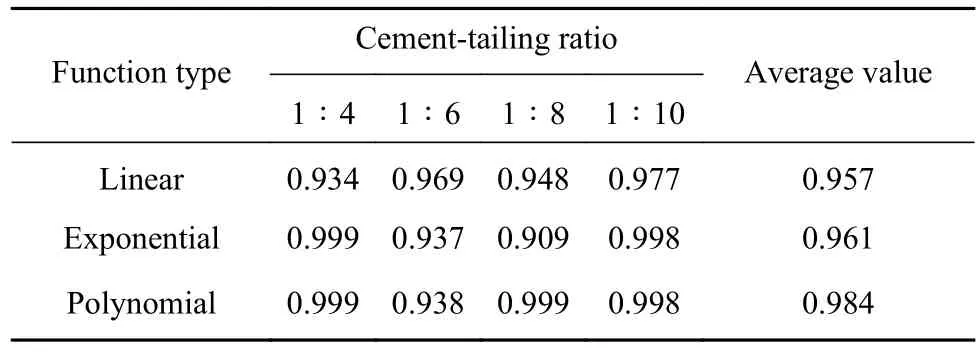
表 4 拟合复相关系数(R2)Table 4 Fitting complex correlation coefficient (R2)

观察图5可知，分层充填体弹性模量随高度比增大而减小. 当高度比为0.2时，灰砂比为1∶4、1∶6、1∶8和1∶10的试件弹性模量分别为233.4、211.8、185.0和166.8 MPa；高度比增大至0.4时，对应的弹性模量分别减小为230.6、203.6、182.2和161.8 MPa，降幅分别为1.2%、3.9%、1.5%和3.0%；继续增加高度比至0.6，对应的弹性模量和降幅分别为224.9、199.9、173.6、153.9 MPa和2.5%、1.8%、4.7%、4.9%；当高度比达到0.8时，对应的弹性模量和降幅分别为216.8、191.2、169.2、144.9 MPa和3.6%、4.4%、2.5%、5.8%.

同样采用线性函数、指数函数及多项式函数对分层充填体弹性模量与高度比之间的关系进行拟合，拟合复相关系数（R2）如表4所示.

由表4可知，三种函数都能较好地表征弹性模量与高度比之间的内在关系，其平均值分别为0.957、0.961和0.984，最大值分别为0.977、0.999和0.999. 但多项式函数复相关系数（R2）平均值相比另外两种函数更大，因此认为分层充填体弹性模量与高度比之间符合多项式函数关系，其表达式可表示为：

其中，E为弹性模量，MPa；A3、B3和C3表示与高度比及灰砂比相关的参数.

2.2.2 灰砂比的影响

图5 高度比与弹性模量关系. （a）线性拟合；（b）指数拟合；（c）多项式拟合Fig.5 Relationship between height ratio and elastic modulus: (a) linear fitting; (b) exponential fitting; (c) polynomial fitting

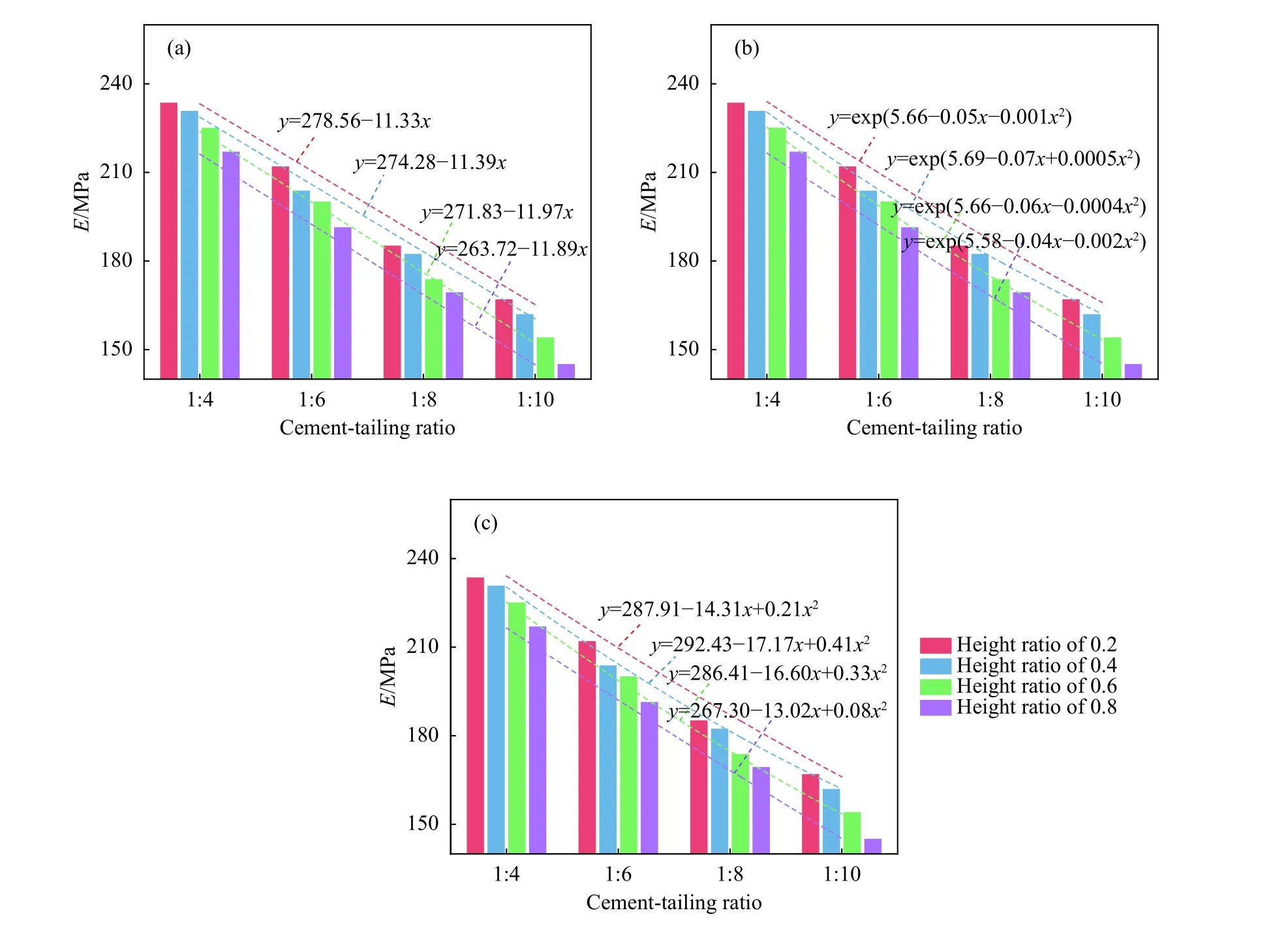
图6 灰砂比与弹性模量关系. （a）线性拟合；（b）指数拟合；（c）多项式拟合Fig.6 Relationship between cement-tailing ratio and elastic modulus: (a) linear fitting; (b) exponential fitting; (c) polynomial fitting

分层充填体弹性模量与灰砂比密切相关，图6为分层充填体弹性模量与灰砂比之间的关系曲线. 分析图6可知，不同高度比分层充填体试件弹性模量随灰砂比增大而增大. 当灰砂比为1∶4时，高度比为0.2、0.4、0.6和0.8的试件弹性模量分别为233.4、230.6、224.9和216.8 MPa；当灰砂比减小至1∶6时，试件弹性模量分别减小至211.8、203.6、199.9和191.2 MPa，减小幅度分别为9.3%、11.7%、11.1%和11.8%；继续减小灰砂比至1∶8时，对应弹性模量值及减幅分别为185.0、182.2、173.6、169.2 MPa和12.7%、10.5%、13.2%、11.5%；当灰砂比减小至1∶10时，对应弹性模量值及减幅分别为166.8、161.8、153.9、144.9 MPa和9.8%、11.2%、11.3%、14.4%.

继续采用线性函数、指数函数及多项式函数对弹性模量与灰砂比之间的关系进行拟合，结果如表5所示.

分析表5可知，三种拟合函数复相关系数平均值分别为0.977、0.988和0.996，对比结果表明，多项式函数能更好的表征分层充填体弹性模量与灰砂比之间的内在关系，其表达式为：

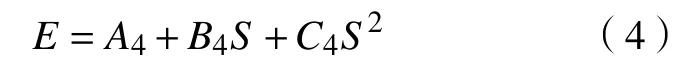
其中，A4、B4和C4为与灰砂比及高度比相关的参数.

2.3 影响因素及敏感度分析

2.3.1 影响因素分析

本文主要研究分层充填体中间层高度比及灰砂比对其单轴抗压强度及弹性模量的影响. 通过前面的分析可知，分层充填体单轴抗压强度及弹性模量随高度比的增加而降低，随灰砂比的增加而增加. 众所周知，充填体力学特性与水泥用量密切相关，水泥用量越多，充填体经过水化反应后形成的水化硅酸钙（C-S-H胶凝体）越多，进而导致尾砂与水泥之间的粘结越充分，最终提高充填体的单轴抗压强度和刚度特征. 灰砂比越大，充填体中水泥含量越少，水化形成的C-S-H胶凝体越少，水泥与尾砂之间的粘结越不充分，导致更低的强度及刚度. 高度比越大，低灰砂比区域占比越多，即软弱区域体积增大，进而导致充填体强度及刚度降低. 分层充填体单轴抗压强度及刚度随高度比增加而降低，本质也是水泥含量变少，水泥与尾砂粘结不够充分，水化形成的C-S-H胶凝体减少所致.

2.3.2 因素敏感度分析

由上述分析可知，分层充填体单轴抗压强度与其高度比及灰砂比密切相关，但两种因素对单轴抗压强度的影响各有差异，即单轴抗压强度对二者的敏感度不同. 为分析单轴抗压强度对各因素敏感度的差异，对分层充填体单轴抗压强度与高度比、灰砂比关系曲线进行分析，结果如图7所示.

表 5 拟合复相关系数(R2)Table 5 Fitting complex correlation coefficient (R2)

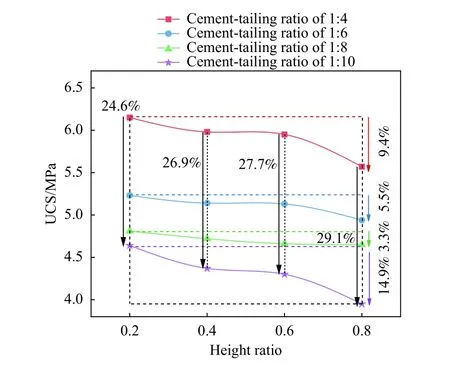
图7 分层充填体强度敏感度曲线Fig.7 Strength sensitivity curve of interbedded backfill

观察图7可以看出，当灰砂比为1∶4时，高度比从0.2增加至0.8，其单轴抗压强度降低约9.4%；当灰砂比为1∶6时，高度比从0.2增至0.8，其单轴抗压强度降低约5.5%；当灰砂比为1∶8时，对应的单轴抗压强度降低约3.3%；当灰砂比为1∶10时，对应的单轴抗压强度降低约14.9%. 对于不同的灰砂比，当分层充填体厚度从0.2增加至0.8时，其单轴抗压强度平均降低约8.3%. 同理，当高度比分别为0.2、0.4、0.6和0.8时，灰砂比从1∶4降低至1∶10的过程中，其单轴抗压强度分别降低约24.6%、26.9%、27.7%和29.1%，平均降低约27.1%. 对比结果表明，灰砂比对分层充填体单轴抗压强度影响更大，即单轴抗压强度对灰砂比敏感度更高.

分层充填体弹性模量也与高度比及灰砂比相关，为分析弹性模量对各因素敏感度的差异，对分层充填体弹性模量与高度比、灰砂比关系曲线进行分析，结果如图8所示.

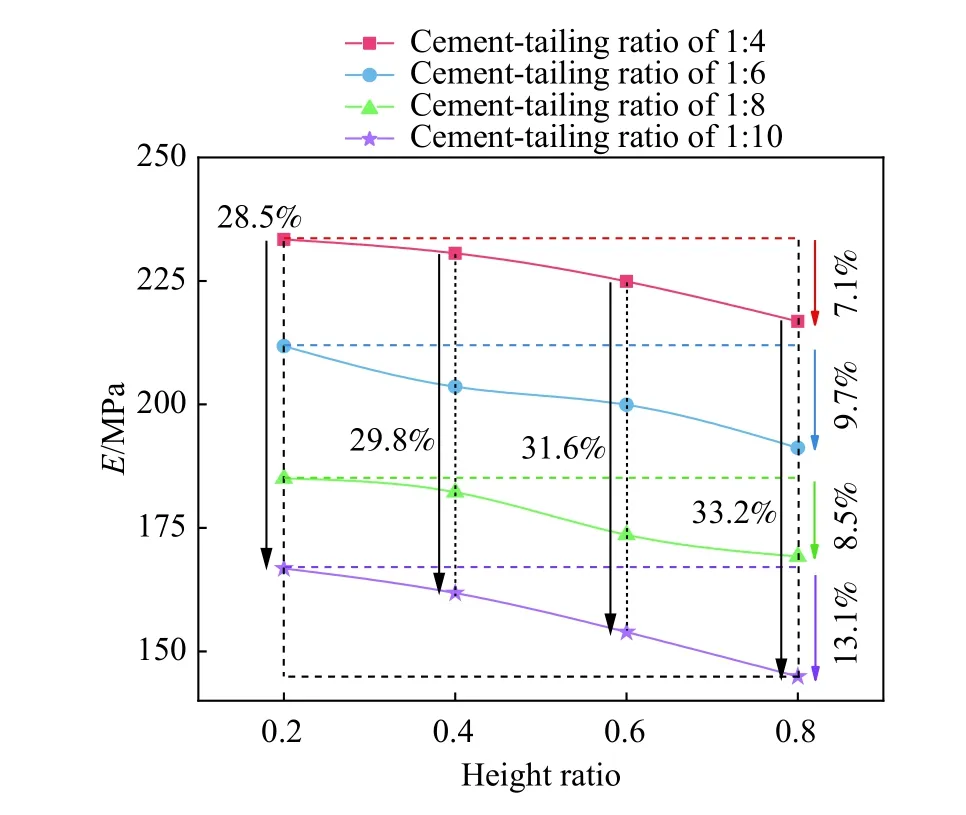
图8 分层充填体弹性模量敏感度曲线Fig.8 Elastic modulus sensitivity curve of interbedded backfill

观察图8可以看出，当灰砂比分别为1∶4、1∶6、1∶8和1∶10时，高度比从0.2增加至0.8的过程中，分层充填体弹性模量分别减小约7.1%、9.7%、8.5%和13.1%，平均减小约9.6%. 当高度比分别为0.2、0.4、0.6和0.8时，灰砂比从1∶4减小至1∶10的过程中，其弹性模量分别减小约28.5%、29.8%、31.6%和33.2%，平均减小约30.8%. 对比分析表明，灰砂比对分层充填体弹性模量影响更大，即弹性模量对灰砂比敏感度更高.

3 分层胶结充填体破裂的细观数值模拟

3.1 细观结构模拟

关于尾砂胶结充填体单轴和三轴压缩数值模拟试验，国内外许多学者[25]利用DEM、PFC等软件开展过相关研究. 通过前文研究可知，充填体强度的增长实质为C-S-H胶凝体（即尾砂与水泥遇水混合后发生水化反应生成的粘结体）数量的增加，而胶凝体数量又与胶结剂（即水泥）含量密切相关，因此可从胶结颗粒数量入手进行数值分析.借助PFC-2D颗粒流程序，构建两种颗粒模型分别模拟尾砂颗粒和胶结颗粒，其中尾砂颗粒与尾砂颗粒之间无黏结作用，尾砂颗粒与胶结颗粒、胶结颗粒与胶结颗粒之间构建平行黏结，以此来模拟水化反应产生的胶凝体.

3.2 颗粒分布模拟

模型中尾砂颗粒级配与真实尾砂颗粒级配一致并作简化处理，如图9所示.

忽略真实尾砂粒径分布曲线末端数据，被忽略的尾砂末端体积采用相应的最小和最大颗粒补充，真实尾砂粒径分布曲线为相应粒径尺寸下的体积比. 胶结颗粒半径参考Fu等[26]的研究设定为3.0×10-4m，胶结颗粒半径稍小于最小尾砂颗粒半径.

图9 尾砂真实粒径分布与模拟颗粒对比Fig.9 Comparison of the true grain-size distributions in tailings and the simulation particles

室内试验样品是直径为50 mm、高度为100 mm的圆柱体，数值计算模型是长度为100 mm、宽度为50 mm的矩形. 首先，在矩形内按照相应级配随机形成具有一定孔隙率的尾砂颗粒，代表真实的没有进行胶结的尾砂，然后在尾砂颗粒间隙随机生成确定数量的胶结颗粒，胶结颗粒数量的增加或减小代表着充填体水化产物的增加或减少. 为了减少计算时间，颗粒半径统一放大10倍.

3.3 参数标定

不同模型两种颗粒细观力学参数均为相同值，只改变胶结颗粒数量，模型细观力学参数参考Liu等[27]的研究并作相应的调整，如表6所示. 通过给模型顶、底部墙体分别施加向下和向上的运动速率来模拟位移加载控制的单轴压缩试验，墙体运动速率设定为0.02 m·s-1，当试件发生破坏时停止加载，在此过程中，通过 Fish语言编写程序，记录整个加载过程中的应力、应变和微裂隙数量.

3.4 模型构建

本次模拟的模型尺寸与方案均与室内试验试件尺寸和方案一致，不考虑料浆质量浓度和养护龄期的影响（设定料浆质量分数为75%、养护龄期为58 d），仅分析中间层灰砂比和中间层高度比对充填体整体力学特性的影响规律. 分层充填体不同分层之间接触采用光滑节理接触，接触模型力学参数见表6，分层充填体数值模型如图10所示.模拟过程中，模型周围不施加任何边界条件，上下端部则采用伺服机理模拟位移控制的实验条件.

3.5 裂纹演化规律分析

充填体发生破坏的过程实质是其内部裂纹萌生、扩展直至贯通的过程，因此研究其内部裂纹演化规律意义重大. 图11所示即为分层充填体裂纹演化规律曲线，篇幅所限，仅列举高度比为0.4和0.6、灰砂比为6和8的分层充填体裂纹演化曲线图.

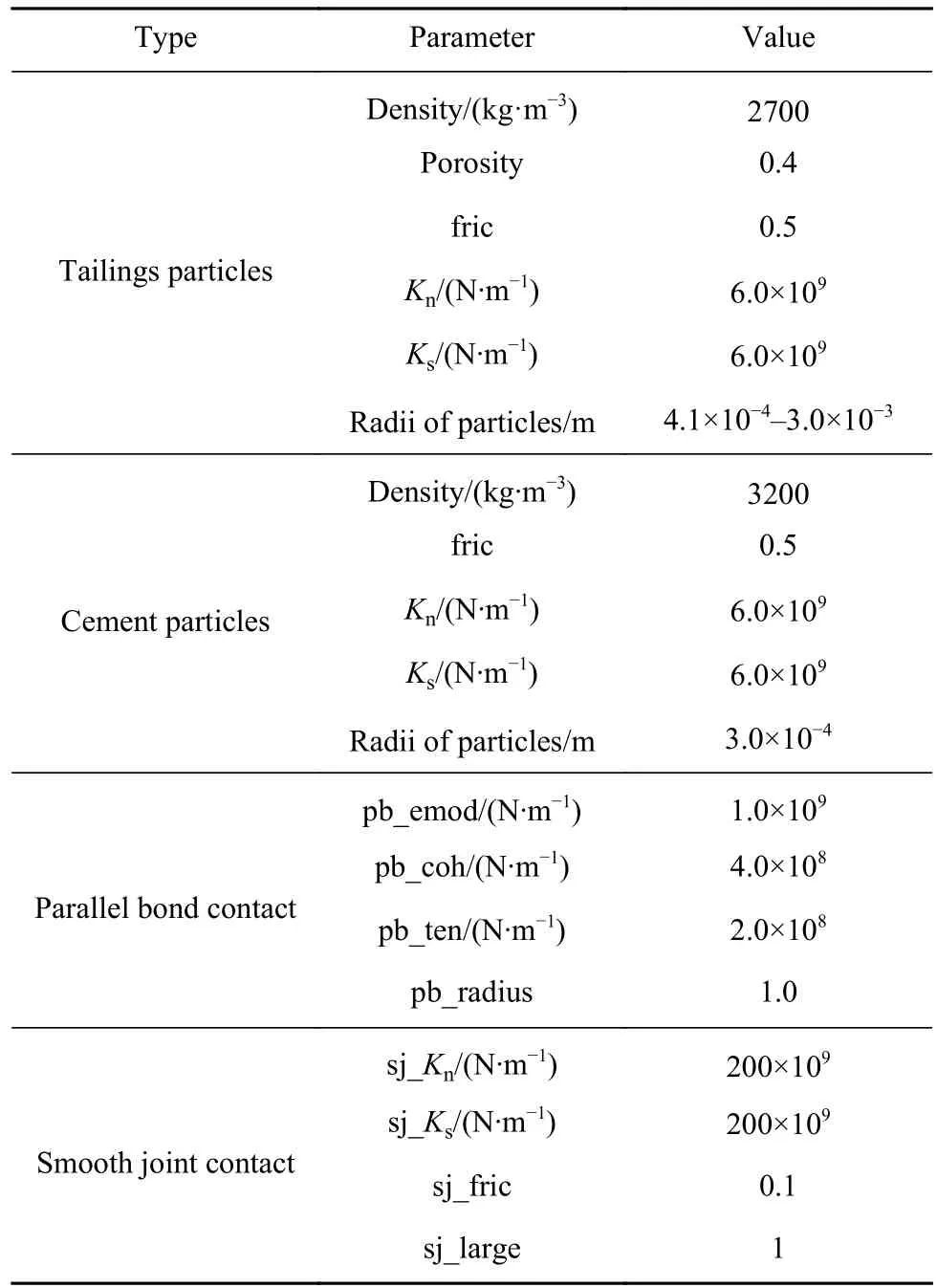
表 6 数值模型细观力学参数Table 6 Meso-mechanical parameters of numerical model

从图11（a）和（b）可以看出，保持中间层高度比不变，灰砂比越小，裂纹演化曲线拐点到来越早，表明裂纹快速增长点越快到来，分层充填体越易发生破坏. 灰砂比越大，试样彻底破坏后裂纹数量越多. 从图12（c）和（d）可以看出，保持灰砂比不变，高度比越大，裂纹演化曲线拐点到来越早，表明裂纹快速增长点越快到来，分层充填体越易发生破坏. 试样彻底破坏后裂纹数量随高度比减小而增大.

图12为分层充填体应力-应变曲线、裂纹演化曲线及裂纹增量曲线复合图，篇幅所限，仅列举高度比为0.4、灰砂比分别为1∶4和1∶8的两个试件曲线图.

图10 分层充填体数值模型细观结构（顶底层灰砂比为1∶4、中间层灰砂比为1∶8、中间层高度比为0.4）Fig.10 Microstructure of numerical model of interbedded backfill (The cement-tailing ratio of top and bottom layer is 1∶4, the cement-tailing ratio of middle layer is 1∶8, and the height ratio of middle layer is 0.4)

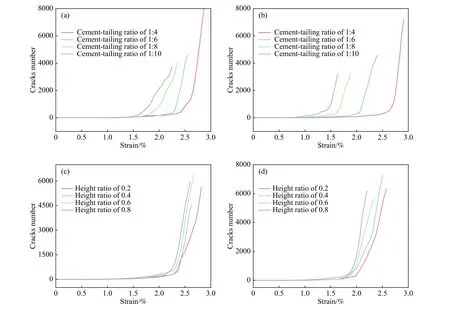
图11 不同分层充填体裂纹演化规律. （a）高度比为0.4；（b）高度比为0.6；（c）灰砂比为1∶6；（d）灰砂比为1∶8Fig.11 Cracks evolution of different interbedded backfills: (a) height ratio of 0.4; (b) height ratio of 0.6; (c) cemented-tailings ratio of 1∶6;(d) cemented-tailings ratio of 1∶8

观察图12可以看出，分层充填体应力-应变曲线初期，内部颗粒之间接触力小于颗粒之间黏结键强度，颗粒间黏结键未发生破坏，分层充填体内部无裂纹产生；随着加载的进行，颗粒间接触力慢慢增大，开始超过其黏结键强度，黏结键被破坏，内部开始产生裂纹，裂纹增量曲线开始出现波动；继续施加荷载，越来越多颗粒间接触力超过其黏结键强度，更多的黏结键被破坏，此时内部裂纹开始增加，裂纹增量曲线缓慢上升；持续施加荷载，外部荷载慢慢达到单轴抗压强度80%时，裂纹累积曲线出现拐点并迅速上升，裂纹增量曲线也出现跃升；继续施加荷载，应力-应变曲线开始出现下降趋势，裂纹累积曲线继续保持高速增长，裂纹增量曲线稳定在较高水平. 总体而言，随着应力-应变曲线的发展，裂纹累积曲线先缓慢增加、然后快速增加、最后增速又开始放缓，裂纹增量曲线先在较低水平波动、然后快速上升、最后又出现一定程度下降并处于较高水平进行波动.

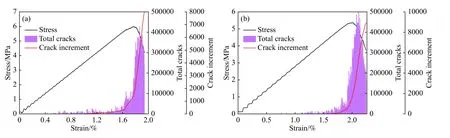
图12 分层充填体应力-应变曲线、裂纹累积曲线及裂纹增量曲线复合图. （a）高度比0.4、灰砂比1∶4；（b）高度比0.4、灰砂比1∶8Fig.12 Composite plots of stress-strain curve, crack cumulative curve and crack increment curve of interbedded backfills: (a) height ratio of 0.4 and cemented tailings ratio of 1∶4; (b) height ratio of 0.4 and cemented tailings ratio of 1∶8

3.6 破坏模式分析

表7所示为不同分层充填体试件破坏模式及分析. 综合分析可知，分层充填体试件主要表现为三种破坏模式：剪切破坏伴随次生剪切裂纹、张拉破坏伴随次生张拉裂纹以及共轭剪切破坏伴随次生拉剪破坏. 保持中间层灰砂比不变，随中间层高度比增加，试件内部裂纹密度越大，试件也由单一破坏模式向多种破坏模式并存过渡. 保持中间层高度比不变，当中间层灰砂比越小，试件内部裂纹越集中于中间软弱层，随着灰砂比增加，软弱层破坏逐渐向试件顶底段延伸、贯穿，然后导致整体失稳破坏.

4 结论

（1）分层充填体单轴抗压强度与高度比呈指数函数关系、与灰砂比呈二次多项式函数关系；弹性模量与高度比及灰砂比均呈二次多项式函数关系. 分层充填体单轴抗压强度及弹性模量均随高度比及灰砂比增大而增加，且两者对灰砂比敏感度更高.

（2）保持高度比不变，灰砂比越小，裂纹演化曲线拐点到来越早，表明裂纹快速增长点越快到来，分层充填体越易发生破坏；保持灰砂比不变，高度比越大，裂纹演化曲线拐点到来越早，表明裂纹快速增长点越快到来，分层充填体越易发生破坏.

（3）分层充填体试件主要表现为三种破坏模式：剪切破坏、张拉破坏及共轭剪切破坏，且破坏主要集中在中间软弱层；保持灰砂比不变，随高度比增加，试件内部裂纹密度越大，试件由单一破坏模式向多种破坏模式并存过度；保持高度比不变，当灰砂比减小，试件内部裂纹越向中间软弱层集中，随着灰砂比增加，软弱层破坏逐渐向试件顶底部延伸、贯穿.