基于变步长LMS减噪的基音检测改进算法

郭琪雯，陈福恩

(北京交通大学 电子信息工程学院，北京 100044)

0 引 言

目前常用的基音检测[1]方法中，ACF法[2]易出现基音半频、倍频错误，AMDF法[3]常会出现均值下降的现象，倒谱法[4]的检测误差受噪声影响较大。

针对上述方法在噪声环境下的检测精度不够理想的问题，近年来许多学者提出了改进的基音检测算法。潘峥嵘等[5]提出了将经过经验模式分解的AMDF与ACF进行加权的基音检测算法，有效减少了半频、倍频的错误，但其算法较为复杂。徐昕等[6]提出通过基于听觉掩蔽的多频带谱减法对带噪语音进行减噪，再利用多门限法判决清浊音并加权ACF、AMDF进行基音检测，其检测正确率在信噪比很低的情况下仍较为理想，但谱减法对于非平稳的语音信号会产生一定的检测误差。

在信号处理中，LMS滤波是自适应滤波算法中最常用的方法之一，而变步长LMS自适应滤波不仅继承了传统LMS算法的优点，还同时兼顾了快速收敛和低稳态失调误差，能很好地处理信号中的噪声[7]。基于以上分析，本文将变步长LMS自适应滤波减噪与基音检测两者结合起来。首先利用变步长LMS自适应滤波器对带噪语音信号进行减噪，将减噪后的语音作为待处理信号，基于其自相关函数、平均幅度差函数以及倒谱建立非线性组合函数，通过检测峰值提取基音周期，判断所得结果是否在置信区间并处理野点，从而更准确地定位基频点。实验结果表明，该算法与传统的方法相比平滑了基音轨迹，准确性更高，且在信噪比为-5 dB的环境下仍可得到较准确的结果。

1 算法基本原理

1.1 变步长LMS自适应滤波

最小均方误差(LMS)算法是在迭代过程中根据输入信号估计梯度矢量并更新权系数，最终使得输出最优的自适应迭代算法。其准则是使滤波器的输出信号与已知期望响应之间误差的均方值最小[8]，理论基础是梯度最陡下降方法。

如图1所示，输入信号矢量为X(n)=[x1(n),x2(n),…,xM(n)]T，滤波器的权矢量为W(n)=[w1(n),w2(n),…,wM(n)]T，d(n)为期望输出信号，实际输出为

y(n)=WTX(n)

(1)

则误差估计可表示为

e(n)=d(n)-y(n)

(2)

将式(1)带入式(2)，两边取数学期望后得均方误差为

E[e2(n)]=E[d2(n)]-2E[d(n)XT(n)]W+
WTE[X(n)XT(n)]W

(3)

由式(3)可看出均方误差是权向量的二次函数，因此为了得到最小均方误差，选择采用最陡下降法寻求加权矢量的最优值，即先设置一个权初值W(0)，权向量的所有分量在每个迭代周期发生改变[9]，沿着负梯度方向不断调整W，其迭代公式为

(4)

(5)

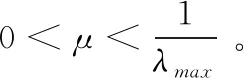
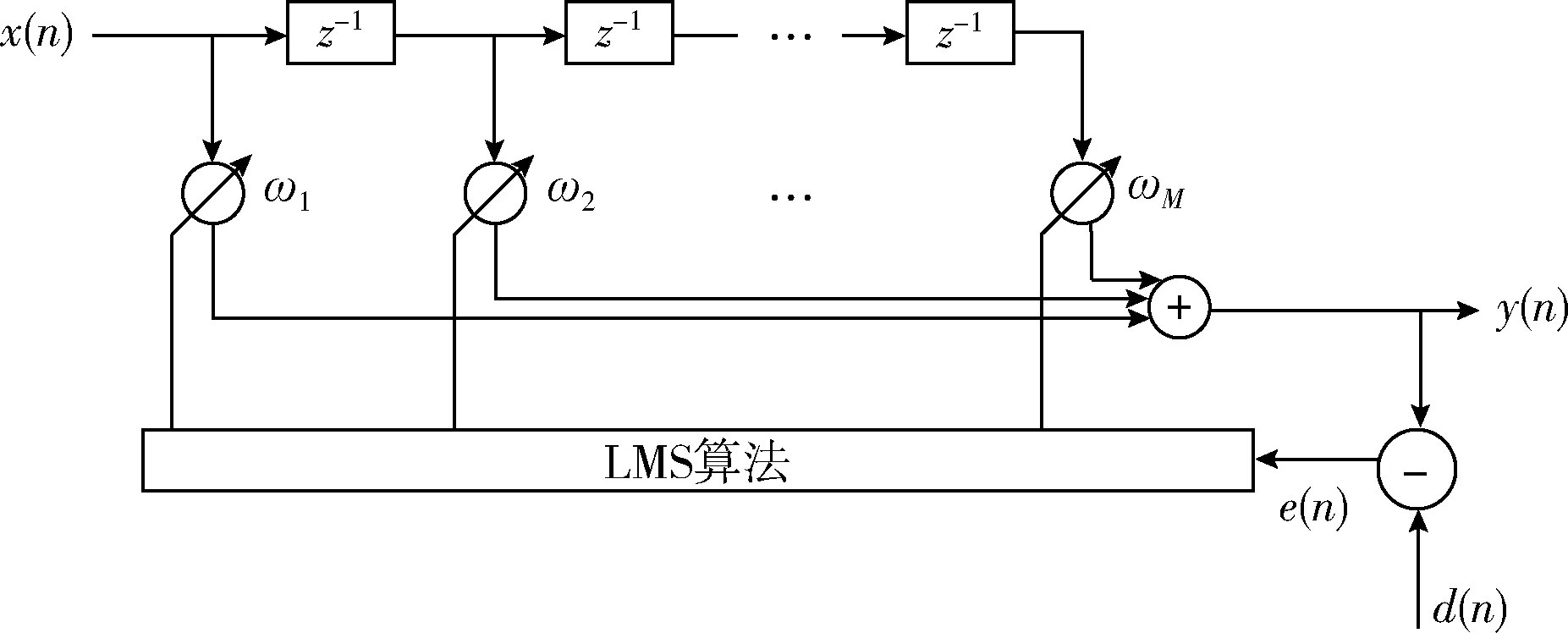
图1 LMS算法原理

在固定步长LMS算法中，滤波器的延迟导致输出的语音波形前端仍有较大噪声，通过增大步长因子μ值可加快收敛速度，减少自适应滤波器初始端的延迟量，但μ值增大同时会减小滤波后的信噪比，增大稳态误差。因此本文采用一种基于Sigmoid函数的变步长LMS算法，其步长因子μ(n)是误差e(n)的Sigmoid函数[10]，表达式为

(6)

1.2 改进的基音检测算法

1.2.1 短时自相关函数(ACF)

对于一语音信号x(n)，经加窗分帧后得第i帧语音信号为xi(m)，则其短时自相关函数可表示为如式(7)所示

(7)

式中：k是时间的延迟量。

由于语音信号中只有浊音帧具有周期性，所以浊音帧的自相关函数也是周期信号，且两者周期相同，若设周期为T，则可知在延迟量为0，±T, ±2T，…时浊音帧的自相关函数达到峰值，因此可以通过检测峰值的位置计算出基音周期。

1.2.2 改进短时平均幅度差函数(MAMDF)

第i帧语音信号的短时平均幅度差函数可表现为如式(8)所示

(8)

对于呈周期性的浊音帧，其短时平均幅度差函数也具有与浊音周期一致的周期特性，而不一样的是短时平均幅度差函数在基音周期的整数倍上不是达到峰值，而是谷点值。由于检测谷值不如峰值方便，因此通过线性变换将寻找谷值转换为寻找峰值[11]。

平均幅度差函数的极大值可连成一条负斜率的直线，把该直线与短时平均幅度差函数之间的差值做线性变换

(9)

式(9)中Di,max是Di(k)的最大值，其对应的位置是ni,max，N为负斜率直线与x轴交点的横坐标，DiM(k)是线性变换后改进的AMDF，称为MAMDF，从而可以实现谷值向峰值的转变，则直接检测峰值即可获取基音周期。

1.2.3 倒谱

信号序列x(n)的倒谱是将其幅值谱取对数后再进行傅里叶逆变换而得到的，表示为

(10)

式中：FT和FT-1分别表示傅里叶变换和逆变换。

由语音的数字信号模型可知，若不考虑口唇端辐射，语音x(n)可看作是由声门脉冲激励u(n)经声道响应v(n)滤波所得的信号[12]，即

x(n)=u(n)*v(n)

(11)

将式(11)左右两端同时取倒谱得

(12)

由式(12)可知包含基音信息的声门脉冲倒谱可与声道响应倒谱分离，浊音信号的周期性激励在倒谱上也有着相同周期的冲激，因此可以通过检测倒谱波形的峰值估算出基音周期。

然而以上3种方法单独使用时都有各自的缺陷，如ACF函数法会出现半频或倍频的误判，倒谱法的检测结果易受噪声影响，无法获得较理想的基音检测结果。分析可知，语音信号第i帧所求的短时自相关函数Ri(k)、改进MAMDF值DiM(k)以及倒谱Bi(k)周期性基本一致，因此本文建立了一个非线性组合函数，记作

Wti(k)=Rni2(k)×(DiM(k)+Bi(k))

(13)

为了避免函数Wti(k)的幅值过大而影响基音检测结果，式(13)中的Rni(k)取第i帧短时自相关函数Ri(k)的归一化值。通过检测Wti(k)的峰值来计算基音周期，目的是在现有方法的基础上更加突出基音周期处的峰值，从而提高基音检测的准确性。

1.3 基频平滑处理

通过上述方法进行基音检测后，所求基音频率曲线仍会出现有些基频值明显偏离了正常值的现象，为了去除这部分野点需要对其作平滑处理。首先，求出每一帧Wti(k)的峰值所对应的位置pi(即延迟量)，其次计算出其平均值m和标准差t，并设置一个置信区间为(m-t+2,m+t-2)，对于标准差很小的计算结果不作处理，而当标准差大于2时，对于Wti(k)峰值所对应的延迟量不在置信区间内的帧，即pim+t-2搜寻其与前一帧Wti-1(k)峰值差值最小的峰值，并将该峰值所对应的延迟量作为当前帧的标准延迟量，从而更正该帧的基音周期值。

(14)

若|Fr(i)*2-Fr(i-1)|<25，则将该帧的基频值更改为如式(15)所示

Fr(i)’=Fr(i)*2

(15)

这样可以更有效地消除半频、倍频错误对于基音检测结果的影响。

2 复合算法实现

本文提出的改进基音检测算法流程可分为语音信号的预处理，变步长LMS减噪，归一化ACF函数、MAMDF函数和倒谱的非线性组合函数计算，基音周期、基音频率的提取以及平滑处理。具体流程框架如图2所示，其步骤总结如下:

(1)对语音信号x(n)进行加窗分帧，并利用能熵比法进行端点检测；

(2)使用带宽为60 Hz～500 Hz的椭圆带通滤波器对x(n)进行初滤波，以减少共振峰和低频噪声的干扰；

(3)对预处理后的语音信号采用变步长LMS自适应滤波器进行降噪；

(4)分别计算降噪后信号的短时自相关函数归一化值、改进短时平均幅度差函数以及倒谱，然后求其非线性组合函数Wti(k)，找到每一帧Wti(k)的峰值所对应的位置pi，对于pi不在置信区间内的所在帧进行纠正，从而得到基音周期;

(5)计算基音频率并通过判断相邻帧的基频差值，做进一步的平滑处理。

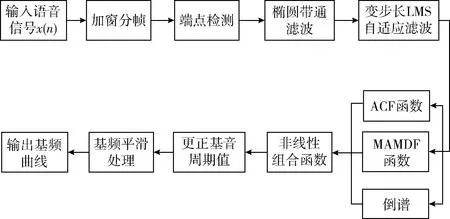
图2 基音检测改进算法的流程

3 实验结果与分析

为了验证本文提出的改进基音检测方法的有效性，使用MATLAB软件进行仿真实验。实验中采用的语音样本是计算机声卡在安静环境下录制的wav格式语音文件，采样频率为8000 Hz，量化比特为16 Bit，分帧帧长取为200采样点，帧移取为100采样点。

3.1 实验一：语音减噪效果仿真

选用一时长约5 s的女声录音文件作为实验样本，通过添加高斯白噪声分别生成信噪比为5 dB、0 dB以及-5 dB的带噪语音。利用变步长LMS滤波器对这3种语音信号的减噪效果分别如图3(a)～图3(c)所示，由图可知该方法在3种不同情况下都使信噪比得到了大幅度提升，5 dB时信噪比提高到17 dB，0 dB时信噪比提高到约15 dB，即使在信噪比为-5 dB的情况下，经过滤波后的语音信噪比也提高到12 dB，减噪效果显著。

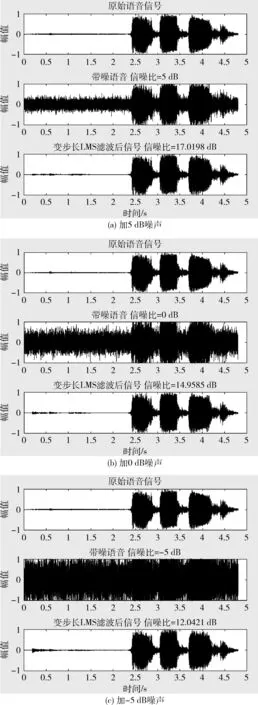
图3 不同信噪比情况下的变步长LMS滤波效果

3.2 实验二：基音检测效果仿真

取实验一中的一帧去噪语音，分别计算它的ACF归一化值、MAMDF值、倒谱值以及本文建立的非线性组合函数值，其对应的函数波形图分别如图4(a)～图4(d)所示。由图4(a)、图4(b)可知，ACF函数、MAMDF函数在采样点约20的位置都呈现出“伪峰值”，其实际对应于共振峰峰值点。而图4(c)中的倒谱波形波动幅度小，呈现出的峰值相对不尖锐。本文建立的非线性组合函数相较于单一的ACF函数、MAMDF函数、倒谱而言，在周期的整数倍处(采样点约40的位置)峰值更加突出，有效地削弱了“伪峰值”点的影响。

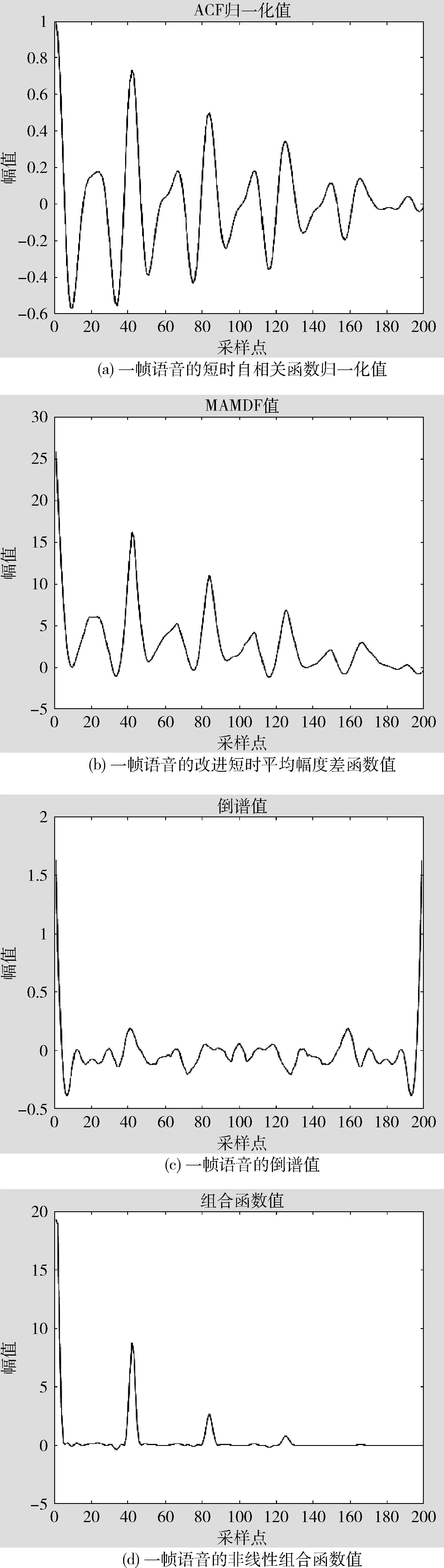
图4 一帧语音的不同函数波形对比

分别用短时自相关函数法、改进短时平均幅度差函数法、倒谱法以及本文方法对实验一中的语音信号进行基音检测，其中信噪比为-5 dB时各方法得到的基音周期如图5所示。图6(a)～图6(d)将每种方法所得基音频率波形放在语谱图上进行对比，可看出单一的ACF函数法、MAMDF函数法以及倒谱法都出现了明显的半频、倍频等误判的情况，而本文方法所求得基频曲线与语谱图上的实际基频曲线重合度很高，几乎无倍频、半频的错误，基频轨迹也相对更加平滑。

图5 不同方法基音检测结果对比

3.3 实验三：鲁棒性效果仿真

为了检验本文方法的鲁棒性，在200组干净语音(其中100组男声、100组女声)中分别加入信噪比为5 dB、0 dB以及-5 dB的高斯白噪声，并以短时自相关函数法加人工校正得到的基音值作为正确参考值，对ACF函数法、MAMDF函数法、倒谱法以及本文方法的基音检测正确率进行比较。

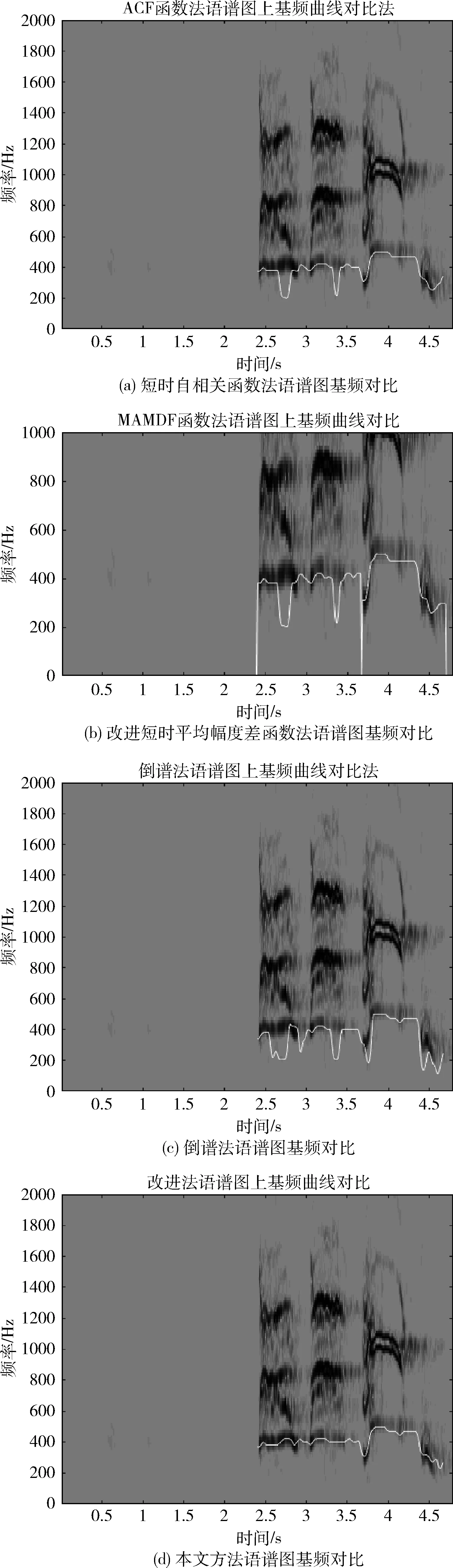
图6 不同方法语谱图上的基频曲线对比

从表1可以看出，在3种不同的信噪比环境下，ACF法、MAMDF法、倒谱法的检测正确率都维持在80%到87%左右，而本文方法的检测正确率一直保持在90%以上，明显高于传统的基音检测方法。即使在信噪比为-5 dB的情况下，正确率也达到了91.9%，比另3种方法都提高了10%左右，从而验证了本文方法具有更高的准确性，且鲁棒性很好。

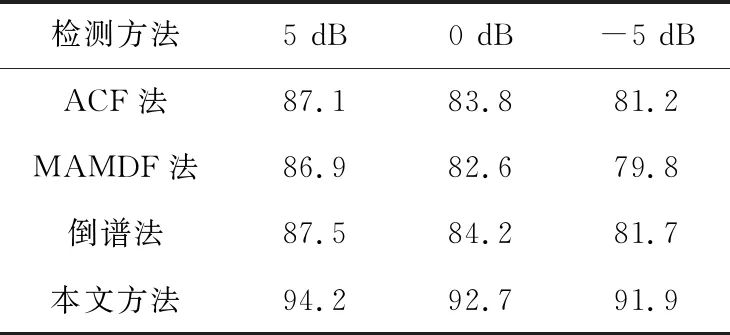
表1 不同方法基音检测正确率对比/%

4 结束语

本文将变步长LMS自适应滤波与组合短时自相关函数、改进短时平均幅度差函数、倒谱三者的基音检测法相结合，提出了一种改进的基音检测算法。首先采用变步长LMS 自适应滤波器对带噪语音进行减噪，其次改进传统的ACF、MAMDF、倒谱法再对减噪后的语音进行基音检测，最后利用置信区间以及相邻基频差值对检测结果做平滑处理。仿真结果表明，本文的改进算法不仅有效地减少了倍频、半频的误判，提高了基音检测的精度，而且即使在信噪比为-5 dB的情况下，检测结果依然明显优于传统算法，鲁棒性最好。