基于用户偏好矩阵填充的改进混合推荐算法

郑小楠，谭钦红，马 浩，刘武启

(1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 信号与信息处理重庆市重点实验室，重庆 400065)

0 引 言

协同过滤推荐算法(collaborative filtering recommendation algorithm，CF)作为推荐算法中应用最普遍的算法之一，被广泛应用于推荐系统中[1]。但是其自身的数据稀疏性[2]、相似度计算不合理等问题都导致了算法推荐质量的严重下降。

针对数据稀疏问题，目前大多数研究采用的是利用评分均值、众数或者中位数等进行填充。这些同等填充方法忽略了用户偏好和物品差异，缺乏一定的可靠性。文献[3,4]通过研究用户对物品的偏好程度和物品相似度对评分缺失项进行了填充。文献[5]通过计算用户的兴趣得分进行矩阵填充，以上方法都以不同的方式降低了数据稀疏率，但未充分考虑用户偏好和物品属性之间的内在联系。

针对相似度问题，文献[6]提出了衡量物品属性的相似度计算方法，文献[7]提出一种基于评分和结构相似度计算物品相似度的方法。文献[8-10]也都针对相似度计算提出了不同改进办法。以上方法均未考虑不同目标用户的偏好。针对以上问题，本文提出了一种改进算法，该算法考虑了用户偏好的权重。根据目标用户的不同，改进物品相似度的计算；最后结合改进的填充算法和相似度计算公式得到基于用户偏好矩阵填充的改进混合推荐算法。该算法不仅大大提高了推荐的准确性，而且还满足了用户的个性化需求。

1 传统的协同过滤推荐算法

首先定义用户集合U={U1，U2，U3，…,Um}，物品集合I={I1，I2，I3，…,In}，用户评分矩阵Rm×n，符号相关概念定义见表1。其中Rui∈[1,5]，当Rui=0时表示用户没有评价该物品。传统的协同过滤推荐算法步骤如下：

步骤1 根据用户评级数据构建用户物品评分矩阵如式(1)所示

(1)

表1 本节公式符号含义

步骤2 根据步骤1构建的评分矩阵，计算用户或者物品间的相似度，获取用户或者物品相似度矩阵。用户相似度计算如式(2)所示，其相似度矩阵为m×m的矩阵，定义为Su，计算结果如式(3)所示。物品相似度计算如式(4)所示，其相似度矩阵为n×n的矩阵，定义为SI，计算结果显示在式(5)中，公式相关概念的定义显示在表1中

(2)

(3)

(4)

(5)

步骤3 对步骤2获取的用户或者物品相似度矩阵进行排序，得到目标用户或物品的近邻集合Uk或In。

步骤4 产生推荐集合。如果采用基于用户的推荐，则可以根据用户a的近邻集合Uk获得尚未评级物品i的用户a对i的预测评级分数Pa,j，如式(6)所示

(6)

类似地，如果采用基于物品的推荐，则根据用户的评分物品计算的推荐集合In可以获得用户a对没有评分的物品i的预测评级分数Pa,i，如式(7)所示

(7)

最后根据从大到小的预测分数，获取目标用户a的推荐集合。

2 本文算法

2.1 融合用户偏好的矩阵填充方法

不同用户对不同物品属性的偏好不同，我们称之为用户偏好。不同物品具有不同的属性，且每个属性对于区别该物品与其它物品的贡献值不同，我们称之为属性权重。文献[5]提出了融合用户兴趣评分的填充方法考虑了物品之间差异性，但未衡量不同用户的物品属性偏好权重。针对以上矩阵填充的缺陷，本文提出了一种基于用户偏好和属性权重的矩阵填充算法。该算法考虑了用户对物品属性的偏好，使填充的数据更可靠，并获得更好的推荐。

不同的物品具有不同的属性，每个属性具有不同的权重值。用户对不同物品的评分差异可以反映用户对不同物品属性的偏好。当填充矩阵时，结合评分数据，分析用户对物品属性的偏好，并计算用户的偏好权重和属性评分均值。然后利用偏好权重和属性评分均值进行计算，计算结果用于矩阵填充，使填充值具有更好的推荐效果。

2.1.1 建立用户偏好矩阵

本节中采用TF-IDF(term frequency-inverse document frequency)的思想，结合用户u对电影I的评分Ru,i进行计算，计算结果代表用户的物品属性偏好权重。TFut在本文的含义是，物品属性t在用户u的已评分物品集合中出现的次数。TFut越大，表示该用户u对物品属性t的喜好越大，越能用该物品属性代表用户的喜好。IDF(t)在本文的含义是，物品属性t在整个物品集合中出现的次数。IDF(t)越大，表示物品属性t对区别不同用户喜好的贡献越少。因此本文使用下面的式(8)定义了用户u对物品属性t的偏好，相关公式符号含义见表2。

表2 公式含义

P(u,t)=TFut×IDF(t)

(8)

(9)

(10)

用户对物品的评级代表了用户对物品属性的主观偏好。在式(8)～式(10)中，如果物品属性t在用户已评分物品中经常出现，并且TFut值比较大，这意味着用户对物品属性t具有高度偏好，并且用户可能更喜欢具有属性t的物品。如果用户评价了很多包含某一相同元素的物品，但是TFut值比较小，这就表示用户对属性t比较喜好，但是很难获取到具有物品属性t的物品。即推荐具有物品属性t的物品给用户更贴近用户的需求。IDF(t)显示了物品属性t在整个数据集中的流行度。用它对用户偏好进行加权可以保证实验结果不会被流行元素影响。

最后对式(8)～式(10)进行归一化处理，使

(11)

归一化处理后wu,t∈(0,1)。对于用户u，它的偏好向量为wu(wu,1,wu,2,wu,3,…,wu,m)。同理可得用户集中所有用户的偏好向量，进而求出用户的偏好矩阵P(表3)。

表3 用户偏好矩阵

由此计算出了用户对特定物品属性的偏好权重。

2.1.2 计算物品属性评分

结合用户评分数据和物品属性信息可以构建评分矩阵(表4)和物品属性矩阵(表5)。依据用户的评分数据和物品属性，能够得到用户对具体物品属性的评级。

表4 用户-物品评分矩阵

表5 物品属性矩阵

表5中的t=1表示该属性包含在该项中，并且t=0表示该属性未包括在该项中。计算物品属性的用户评分，如式(12)所示

(12)

最后根据计算式(12)的计算结果得到用户-物品属性评分矩阵(表6)。

表6 用户-物品属性评分矩阵

2.1.3 基于用户偏好的矩阵填充

根据表3获取的用户偏好矩阵和表6获取的用户物品属性评分矩阵，填补用户评分缺失项。填补用户的未评级物品时需要考虑两个方面：

(1)未评级物品中包括的所有物品属性都包含在用户已评分物品集的所有物品属性中。在该情况下，采用式(13)计算填充值

(13)

(2)未评级物品中的物品属性未包含在用户的评级物品集中。在该情况下，为了避免不准确的填充值影响后续评分的准确度，不填补该物品。

通过本节提出的算法，填补用户未评分的物品可以很好地缓解评分数据的稀疏性。最后在实验部分对本节提出的填充算法与目前研究中常用的几种填充算法进行对比。

2.2 考虑目标用户的相似度计算方法

传统的CF算法中，相似度的计算没有考虑目标用户不同。简而言之，在进行相似度计算时，两个物品之间的共同评分用户的权重是一样的，目标物品的近邻对所有用户都是一样的。然而合理的假设是，当我们搜寻目标物品近邻时，应该考虑对目标物品和另一物品都评过分的用户间的相似度，为每个目标物品选择不同的近邻。另外，传统的计算方法也未考虑用户的偏好差异。因此本文提出一种考虑用户的偏好差异的相似度算法。该算法从两个方面改进了相似度计算公式：用户偏好和邻居选择。考虑用户偏好，根据目标用户的不同，为每个目标项选择不同的近邻集合，使近邻选择更加合理，提高推荐的精度。

从式(3)可知，当计算两个物品之间的相似性时，首先需要寻找对这两个物品都评过分的用户集合。然后根据用户集合中的用户的评分偏差来计算两个物品间的相似度。对于任何用户来说，物品之间的相似性是相同的，这显然是不合理的。因此，本文中相似度算法改进的第一点是将用户相似度引入到物品相似度的计算中，并在计算物品之间的相似度时，考虑目标用户与已对两个物品进行评分的用户之间的相似性。然后对用户相似度的计算要考虑用户偏好的差异。因此本文对相似度算法改进的第二点是采用表3的用户偏好矩阵，考虑用户之间的偏好差异来计算用户之间的相似性。最后，本文采用的用户相似度的计算如下面的式(14)所示，考虑用户偏好的物品相似度的计算如式(15)所示。其中，公式中的符号含义见表7。

表7 公式含义

(14)

(15)

2.3 基于用户偏好和属性权重的改进混合推荐算法

根据用户对物品属性的偏好权重填充矩阵，然后改进相似度计算公式。为不同的目标用户和不同的目标物品找到更合适的邻居集，然后根据邻居集计算物品评分预测值。最后，提出了一种基于用户偏好和矩阵填充的改进混合推荐算法。

算法：基于用户偏好矩阵填充的改进混合推荐算法

输入：用户评分数据、物品属性信息、邻居数目K

输出：目标用户的预测评分

具体的步骤如下：

(1)计算用户偏好和属性评分均值；

(2)根据(1)中得到的矩阵，采用式(13)的计算结果填充矩阵；

(3)根据(1)中求解的偏好权重计算不同用户间的相似度;

(4)根据(3)计算的结果，考虑目标用户的差异，使用式(15)计算物品之间的相似度;

(5)根据步骤(4)得到的对于不用目标用户的物品相似度，采用如式(16)获取用户没有评分物品的预测值。最后，选择预测值中得分最高的前N项作为目标用户的推荐集。其符号含义见表8

(16)

表8 式(16)符号含义

3 实验与分析

3.1 实验准备

本文的所有实验和算法都是通过MATLAB和Python实现。实验运行PC的操作系统为Windows10，处理器为Intel Core i5-4200U CPU,内存为8 GB。

本文采用的实验数据是Movielens100k数据集，该数据集是推荐算法研究中的常用数据集[11]。为了更好地对本文所提出的算法进行实验对比和分析，选择它作为实验数据集。该数据集有943个用户对1682部电影的100 000条评分数据[11]，除此之外还有用户的基本信息和物品的属性信息等。

3.2 评估指标

为了评估改进的推荐算法的准确度，本文选择平均绝对误差(mean absolute error，MAE)作为评价标准。MAE用来计算物品的预测值和真实值之间的差异，MAE值越小，说明预测值的准确度越高，其计算公式如式(17)所示

(17)

其中，n代表预测评分的个数。

3.3 结果分析

为了保证结果的准确性和可行性，本文将数据集随机分成两部分，80%的数据用于训练,20%的数据用于测试。Movielens数据集由5组随机分割的训练集和测试集组成，这些训练集和测试集在提供的5对数据集上执行。每个实验取5次实验结果的平均值进行分析。

实验1：测试本文提出的缺失项填充算法的有效性。

通过从训练数据中随机选出一些已评分电影作为评分缺失项，然后分别采用用户评分均值填充法(URA)，物品评分均值填充法(IRA)，文献[5]提出的融合用户兴趣评分填充法(UIR)和本文的基于用户偏好的矩阵填充法(UPR)对缺失项进行填充，最后，计算包含不同用户的数据集下的MAE值，实验结果如图1所示。

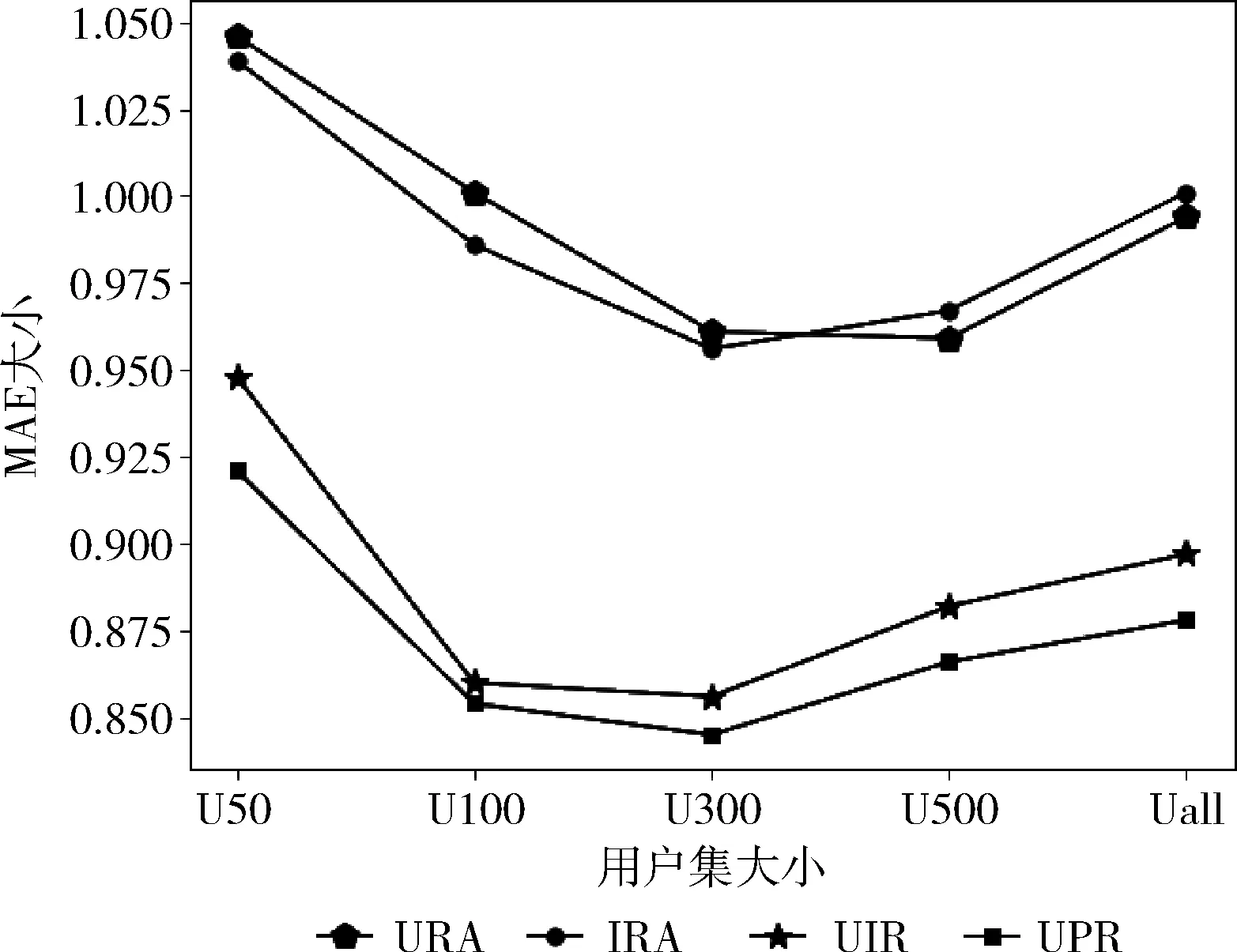
图1 常用填充算法的MAE比较

从图1能够看出，伴随K值的变化，4种算法的MAE都刚开始逐步下降，然后再慢慢上升。这是因为近邻个数的选取需要在一个合适的范围内，过大过小都影响推荐精度。即便如此，采取本文的UPR算法填充评分缺失项的MAE值在包含不同用户数的数据集中都比其它3种填充方法小，准确度至少提升了4.3%。说明在填补用户评级缺失项时考虑用户的偏好权重可以获得更好的推荐。

实验2：检测改进相似度计算的有效性。

为了测试本文改进的相似度计算的有效性，本文将针对以下4种情形进行对比：

(1)计算传统的CF算法的MAE值；

(2)在传统CF算法上采用本文改进的相似度计算，然后再根据推荐结果计算MAE值(CF_S)；

(3)根据本文提出的填充算法采取传统的Pearson相似度计算方法，根据推荐结果计算MAE值(UPR)；

(4)根据本文提出的矩阵填充算法采用的本文提出的相似度计算方法(UPR_S)。

然后将近邻数分别设置为5、10、20、30、40、50、60、70、80、90进行实验，最后根据推荐结果计算MAE值，实验结果如图2所示。

图2 改进相似度算法性能比较

图2的实验结果表明了本文提出的相似度计算方法的可行性。不管是在常规的CF算法上还是在本文提出的填充算法上使用改进的相似度计算方法都比使用传统的相似度计算取得更低的MAE值。在传统算法中引入改进的相似度计算方法，性能提升了2.7%～3.2%，在本文填充算法的基础上提升了2%。说明了本文提出的改进相似度计算方法的有效性。

实验3：测试本文最终提出的算法的有效性

将本文提出的考虑用户对属性的偏好权重的改进混合推荐算法(IHRUP)和传统的协同过滤推荐算法(UBCF)、文献[3]提出的基于评分矩阵填充和用户兴趣的协同过滤推荐算法(PICF)、文献[5]提出的基于用户兴趣评分填充的改进混合推荐算法(IHRIRF)分别在近邻数设置为5、10、20、30、40、50、60、70、80、90时进行实验对比，实验结果如图3所示。

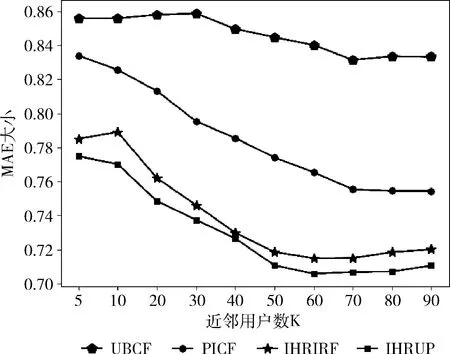
图3 4种算法在不同数量的用户集下的MAE比较

从图3可以看到，随着K值的增加，上述4种算法的MAE值开始下降并最终接近稳定值。对于不同的近邻个数，本文所提出的算法IHRUP均优于UBCF、PICF和IHRIRF算法,相较于UBCF算法，推荐性能提升了12%，相较于PICF算法，推荐性能提升了5.36%，相较于IHRIRF算法，推荐性能提升了0.8%，验证该算法是有效的，可以进一步降低 MAE值，有效提高推荐的准确性。

4 结束语

本文针对现有的填充算法中未充分考虑用户偏好和物品属性内在关联的问题以及相似度计算中存在的不合理之处提出了一种改进算法。该算法依据对用户评分和物品属性的分析，求解出用户的偏好权重和属性评分均值，并据此采用改进的填充算法填补缺失项。同时在相似度计算中，通过考虑目标用户的差异来改进计算公式。最后通过实验与其它CF推荐算法进行比较,结果表明本文改进的算法可以有效改善评分数据稀疏问题，充分考虑了用户的偏好，能满足不同用户的喜好。