水力压裂条件下煤层流固耦合模型的建立及数值模拟研究

赵向东，唐建平

(1.山西燃气集团有限公司，山西 太原 030027； 2.瓦斯灾害监控与应急技术国家重点实验室，重庆 400037； 3.中煤科工集团重庆研究院有限公司，重庆 400037)

煤炭是我国的主体能源，我国是世界上最大的煤炭生产国和消费国[1]。随着煤矿开采深度的不断增加，瓦斯灾害事故频发，同时煤层普遍呈现“三高一低”的特征，即高瓦斯含量、高瓦斯压力、高地应力及低渗透率，且大多数煤层为无保护层开采的单一煤层[2-3]。因此，在抽采瓦斯时需要采取一定的技术措施来增加煤层的渗透率，尽可能地提高瓦斯抽采效率。

常见的煤层增透技术[4-5]主要有水力压裂、水力割缝、高压水射流及深孔爆破技术等，水力压裂技术以其增透效果好、增透范围大而在煤矿生产中被广泛应用。因为水力压裂对煤层的破坏作用较为复杂，导致压裂过后煤层的变化及瓦斯运移规律也相当复杂[6-8]。对于该问题的相关研究，比较常见的有水驱气理论[9-11]，认为高压水进入了煤层之中，压裂孔周围的孔隙压力急剧升高，由于压力梯度的影响，压裂孔周边原先赋存在煤层之中的瓦斯气体向低孔隙压力区域转移。该理论有一定的科学依据，但是液态水驱替的大部分都是游离瓦斯，而且高压水还对吸附气体有一定的封堵效应，吸附在煤层里的瓦斯气体仍然留在原处。与此同时，大多数研究水力压裂后瓦斯的运移规律都未考虑煤层渗透率的变化，导致对压裂影响半径的考察存在一定的误差[12-13]。如何表征水力压裂后煤体的破坏情况，对于客观评价水力压裂及高效抽采瓦斯具有重要的意义。

基于此，笔者构建能够描述水力压裂条件下煤体的损伤特性和煤体损伤—渗流耦合模型，并以寺河矿3309工作面煤层相关物性参数为基础进行水力压裂条件下煤体损伤—渗流耦合数值模拟，为现场水力压裂后瓦斯抽采孔的布置及压裂效果的客观评价提供参考。

1 理论模型

1.1 水力压裂条件下煤体有效应力

根据损伤力学有效应力原理[14-16]，考虑到水力压裂后煤体受损导致弹性模量降低，从而导致有效应力增加，可得到应力—渗流耦合作用下的应力—应变关系：

σ1=E0ε1(1-D)+2νσ3+(1-2ν)αpw

(1)

(2)

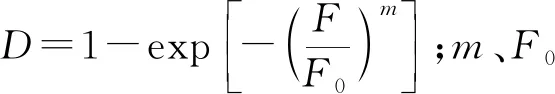
1.2 煤体渗透率和孔隙率动态变化模型

煤体在进行水力压裂过程中，高压水进入煤层，水压力会对煤体产生损伤作用，利用S-D模型[17]可以充分分析在此过程中煤层有效应力的变化趋势，得到水力压裂过程中有效应力原理。

煤岩渗透率和有效应力最终呈现以下的指数关系：

k=k0e-3Cf(σ-σ0)

(3)

式中:k为水力压裂之后的煤层渗透率，m2；k0为煤层初始渗透率，m2；Cf为裂隙压缩系数；σ为应力，MPa；σ0为初始应力，MPa。

水力压裂后，在进行排水降压的初期，煤储层的压力并没有降低到临界解吸压力，瓦斯不会被解吸，此时有效应力的变化可以按下式表示：

(4)

式中:pz为压裂注水压力，MPa；p0为初始瓦斯压力，MPa。

由上述S-D模型可知，裂隙压缩系数的计算公式为：

(5)

式中:q0为初始孔隙率；E为煤体弹性模量，MPa。

众多研究人员针对煤体应力对渗透率的影响做了大量的研究工作[18-19]。大多数研究成果认为随着煤体有效应力的增加，其渗透率呈现下降的趋势。根据式(4)可以看出，随着压裂注水压力的增大，煤体所承受的有效应力下降，渗透率变大。

根据式(3)～(5)可以得出，水力压裂过程中煤体渗透率动态变化模型为：

(6)

在有关研究人员提出的孔隙率和渗透率众多模型中，其中以Kozeny-Carman提出的渗透率k与孔隙率q之间的经典立方定律模型应用得最为广泛，其计算公式如下：

(7)

将改进的渗透率分析模型代入式(6)可得：

(8)

1.3 煤体变形场控制方程

1)平衡方程

根据弹性平衡条件，可以得到多孔介质系统的平衡方程：

σij,j+fi=0

(9)

式中：σij,j为应力张量的分量；fi为体积力分量。

2)几何方程

假设煤岩体变形为微小变形，根据弹性力学理论，则其应变—位移几何方程为：

(10)

式中：εij为应变张量；ui,j、uj,i为轴向和径向位移张量。

3)本构方程

考虑到水力压裂过程中孔隙水压的影响，在引入Biot等效应力的情况下，有效应力可以表述为：

(11)

在仅考虑有效应力的作用下，其应力—应变之间的关系表述为：

(12)

根据以上公式，联立应力平衡及变形协调控制方程，即能得到煤体弹性阶段的变形控制方程：

(13)

本文引入Drucker-Parger强度准则作为煤体微元体损伤程度的判断依据，Drucker-Parger强度准则的表达式为：

(14)

式中：J2为应力偏张量第二不变量；I1为应力张量第一不变量；λ、κ为材料常数，是关于材料C、φ的函数；C为材料黏聚力，MPa；φ为内摩擦角，(°)。

计算当前载荷下的损伤变量D，将损伤后弹性模量E表示为：

E=E0(1-D)

(15)

1.4 水力压裂下煤层瓦斯渗流场控制方程

水力压裂过后，煤层的孔隙压力不断降低，当孔隙压力降低到煤层气临界解吸压力时，储存于煤中的煤层气开始解吸，进而扩散至水力压裂所形成的的裂隙之中，在此过程可以利用Darcy定律来描述瓦斯的渗流过程：

(16)

式中：p为瓦斯压力，MPa；t为时间，s；q为孔隙率；f为气体体积力项；μ为运动黏滞系数，Pa·s；Qs为气体质量源，kg/m3。

对于水在煤层中的渗流过程，水流动计算公式与式(16)相似，只是水的运动黏滞系数ζ与瓦斯的运动黏滞系数μ有所不同。

吸附瓦斯含量符合朗格缪尔变温吸附方程，代入系数取值即可得煤层吸附瓦斯含量方程：

(17)

式中：Q为单位体积煤体的吸附瓦斯含量，kg/m3；A为煤的灰分，%；M为煤的水分，%；a为煤体极限吸附量，m3/kg；b为煤体Langmuir压力参数，MPa-1；ρc为煤体密度，kg/m3；T为煤层温度，K；ρn为标准大气压下瓦斯气体密度，kg/m3。

等温过程煤体中孔隙率的变化情况可表示为：

(18)

将式(6)、(8)及(18)代入式(16)可得到渗流场控制方程。

2 数值模型及结果分析

2.1 几何模型

运用数值模拟软件COMSOL Multiphysics 5.0 (求解器为达西定律和多孔介质模块)，对煤层水力压裂过程进行模拟。煤层水力压裂二维几何模型如图1所示，模型采用的是四边形网格，整个平面网格采用细化的划分方式，在压裂孔网格设置加密，整个模型划分为11 234个单元，网格质量设为1。

图1 煤层水力压裂二维几何模型

数值模拟是基于寺河矿3309工作面煤层的相关物性参数开展的，煤层物理性质参数见表1。

表1 模型煤层物理性质参数

2.2 初始条件和边界条件

初始条件：煤层内部有1.0 MPa的初始瓦斯压力，压裂孔的压力为20 MPa左右。压裂孔直径为0.1 m，承受岩层重量，上部岩层应力约为10 MPa，模拟模型为200 m×16 m的二维模型。

边界条件：瓦斯仅在煤层内流动，模型四周约束方式为辊支承(约束法线方向的位移)，忽略模型的自重载荷。

计算方案：模拟研究在不同压裂时间、不同位置煤层孔隙水压、渗透率的变化。

2.3 计算结果分析

水力压裂压力为20 MPa(压裂时间t=2、4、6、8 h)时孔隙水压力沿煤层走向的分布规律如图2所示，可以看出，距离压裂孔越近，孔隙水压力下降幅度越大。随着压裂时间的延长，压裂影响范围逐渐扩大，压裂8 h时，压裂影响半径达到了50 m以上。

图2 不同压裂时间孔隙水压力沿煤层走向变化图

不同压裂时间水力压裂煤层渗透率沿着压裂孔周围的变化规律如图3所示，可以看出，渗透率的变化与孔隙水压力变化规律一致。

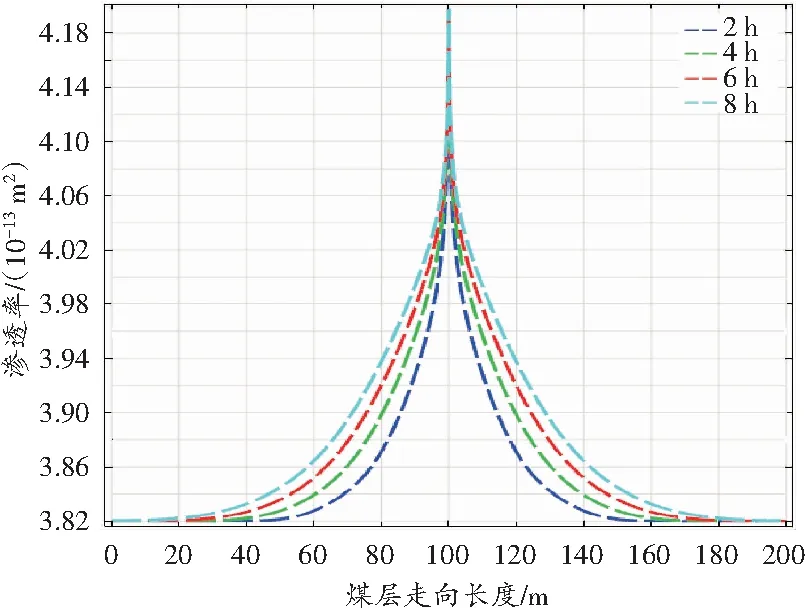
图3 不同压裂时间渗透率沿煤层走向变化图

图4为不同压裂时间煤层孔隙水压力分布云图，可以看出，随着压裂时间的增加，煤层的孔隙压力逐渐上升。结合图2可知，在水力压裂初期，煤层中的孔隙水压力上升较快，随着压裂时间的增加，煤层中孔隙水压力上升幅度逐渐变小。

图4 不同压裂时间煤层孔隙水压力分布云图

图5为煤层压裂孔前方20 m处一点孔隙率随时间的变化曲线，可以看出，随着压裂时间的增加，该点的孔隙率逐渐增大，但是其增大速率逐渐变小。

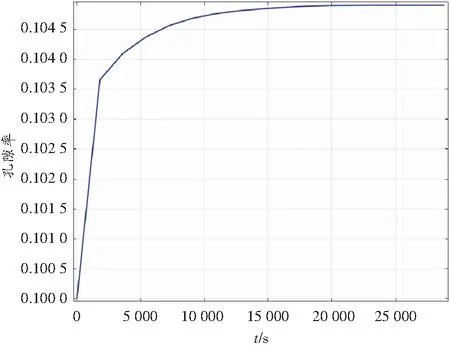
图5 压裂孔前方20 m处煤层孔隙率随时间变化曲线

图6为不同注水压力(20、30 MPa)条件下煤层孔隙水压力变化对比分析图，可以看出，在此煤层条件下，两种注水压力条件下的影响范围大致相同，只是注水压力为30 MPa时在压裂孔处的孔隙水压力下降的幅度稍大。

图6 不同注水压力条件下煤层孔隙水压力变化对比图

根据《防治煤与瓦斯突出细则》中关于瓦斯抽采达标的相关规定，其中的指标之一即钻孔抽采瓦斯后应该使残存瓦斯压力小于0.74 MPa，才能达到防突的要求，当煤层瓦斯压力高于0.74 MPa时，预抽后残存瓦斯压力低于0.74 MPa距钻孔最远的距离为有效抽采半径。在相同瓦斯抽采条件下，当注水压力为20 MPa时，压裂与未压裂煤层钻孔抽采瓦斯压力变化对比曲线如图7 所示。

图7 注水压力20 MPa条件下压裂与未压裂煤层 预抽瓦斯72 h抽采半径对比图

由图7可见，随着煤层瓦斯抽采的不断进行，有效抽采半径增大的速度慢慢地下降，最后接近于一个定值；在注水压力20 MPa条件下，经过压裂的煤层瓦斯有效抽采半径达到9 m，未压裂区域煤层瓦斯有效抽采半径约为3 m，压裂之后的煤层瓦斯抽采有效半径大约是未压裂煤层的3倍。

3 结论

1)基于统计损伤力学及有效应力原理推导出水力压裂条件下煤层的流固耦合模型，并将该模型导入数值软件进行了模拟，结果表明，随着压裂时间的增加，水力压裂影响半径逐渐扩大，并且在压裂时间达到8 h时，压裂影响半径达到了50 m以上。

2)模拟得出在相同煤层条件下不同注水压力对压裂半径的影响，在此煤层条件下，注水压力30 MPa的影响范围与注水压力20 MPa的影响范围大致相同，只是前者在压裂孔处注水压力下降的幅度稍大。模拟得到注水压力20 MPa压裂之后的煤层瓦斯抽采有效半径是未压裂煤层的3倍。