基于R 语言建立SARIMA 滑动窗口模型的日度快递业务规模预测

周 杨，甘陆军，金 龙

（1.圆通速递有限公司，上海 201705；2.物流信息互通共享技术及应用国家工程实验室，上海 201705）

1 绪论

1.1 研究背景和意义

随着快递行业的不断变革以及中国电商行业的快速发展，人们对快递需求量扩大，快递业务量持续增长，中国成为世界发展最快、最具活力的新兴寄递市场。2019年快递服务企业业务量完成635.2亿件，快递业务收入完成7 497.8 亿元，年人均快递使用量为45.4件，年人均快递支出535.5元。中国快递业务量连续6年居全球第一，快递业务量超越美、日、欧发达国家经济体总和。物流行业发展进入量质齐升阶段，快递业也从高速增长阶段转向高质量发展阶段。随着产业升级对物流快递的服务提出了更高要求，在服务质量上要求更富弹性、更加精准、更多层次。

快递行业业务总量是评价快递业务的总体指标，快递行业业务总量的预测对快递行业的发展具有重大意义，而快递业务规模预测中的日度业务量预测对快递企业、政府、快递产业链上下游企业的规划和决策具有重大影响。对于快递企业来说，快递业务规模的预测对人员管理、车辆调配、路由规划以及资金投入等方面产生重大影响，对其进行科学合理的预测可以提高企业科学管理能力，合理分配资源，实现企业降本增效的目的，为企业的经济决策提供重要参考依据。精准的预测可以为中央和地方政府编写政策和规划提供数据支撑和依据，可以为快递产业链上下游的电商、供应链企业在生产经营决策、投资决策、风险评估等方面提供决策参考。

1.2 研究综述

通过一些从研究时间、研究对象、研究方法三个方面分析快递业务规模预测的文献可以得出以下结论：国内学术界对快递业务规模的预测在时间维度上主要集中于年度业务规模预测和月度业务规模预测，对于日度业务规模预测的研究不足；研究对象主要集中于快递行业、区域快递、高校快递的业务规模预测，对于快递企业业务规模预测的研究不足；快递业务规模预测常用的研究方法有组合预测、机器学习神经网络算法、灰色预测以及时间序列预测等方法。

从时间维度上分析研究年度业务规模预测、月度业务规模预测两方面。肖烯岚、戴厚平[1]选取湖南省2010—2019 年的年度快递业务量构建灰色系统GM(1,1)预测模型，模型误差维持在5%左右，运用此模型进行了为期三年的快递业务量预测。李辰颖[2]运用CEEMD-SVM 模型预测月度快递业务量，首先用CEEMD 方法对归一化后的快递业务数据进行分解；然后采用C-C 法对IMF 分量进行相空间重构；再用相空间重构后的数据训练SVM 模型；最后运用训练后的SVM模型预测月度快递业务量。

从研究对象维度上分析研究行业、行政区域、企业、高校等单位的快递业务规模预测方面。朱志锋、肖诗雨[3]通过Eviews8.0软件采用时间序列分析方法，建立ARIMA 模型进行参数估计及检验，对比Holt-Winters季节乘法模型预测结果和实际值进行误差分析，选择ARIMA 季节乘积模型对未来我国快递业务量进行预测。伍平[4]分析北京区域快递需求特征的基础上，使用灰色系统GM模型、BP神经网络模型和多元回归分析模型从不同角度对快递需求进行短期预测，并综合各模型优势最终建立权重组合预测模型。李贞贞[5]选取河南省月度快递业务量，考虑到月度快递业务量的趋势性、季节效应，建立ARIMA简单季节模型对河南省快递业务量进行预测。

1.3 研究方法

本文研究某快递企业分部的日度业务规模预测，通过R 语言软件运用时间序列分析方法建立SARIMA乘积模型，并建立为期三天的滑动预测模型预测日度业务规模。建立SARIMA 模型时首先对数据进行季节分解和检验时间序列数据的平稳性，若序列非平稳则需差分处理使其平稳化，其次观察序列的自相关与偏自相关图估计模型参数，然后对模型拟合初步确定模型，再对模型残差序列进行白噪声检验，通过白噪声检验确定模型，对模型进行残差分析研究从而优化模型，最后根据模型预测值对模型进行评估。其流程图如图1所示。

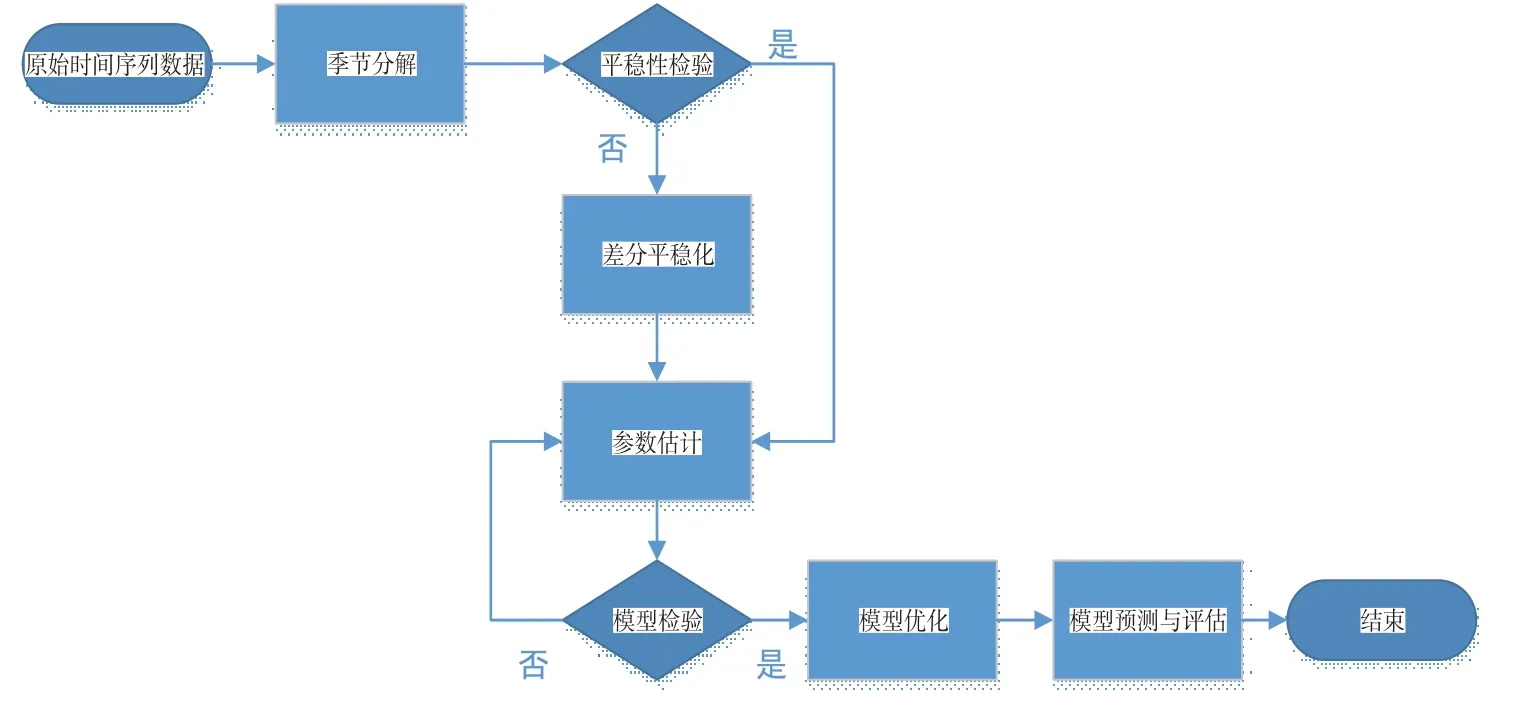
图1 建立SARIMA模型的流程图

2 SARIMA模型简介

在时间序列分析中，某些时间序列存在明显的周期性变化，如季度、月度、周度或是其他一些固有因素引起的变化，这类序列称为季节性序列。对季节性时间序列分析和建模通常采用SARIMA模型，即季节性差分自回归滑动平均模型，模型的一般表达式为：

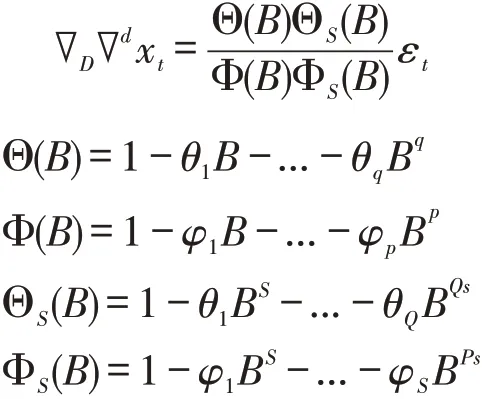
该模型简记为SARIMA(p,d,q)(P,D,Q)S，参数p,q,P,Q分别表示非季节与季节AR、MA算子的最大滞后阶数，d,D 分别表示非季节与季节性差分次数，εt为扰动项，S为序列周期。

3 模型的建立与分析

3.1 数据的获取与预处理

本文获取了某快递企业分公司2016 年1 月1 日至2019 年2 月28 日的日度快递业务量数据，由于数据的保密性，本文将在原有数据的基础上乘以基数k，得到本文研究样本数据，如图2所示。为检验模型的性能，本文将样本数据分为训练样本和测试样本，训练样本为2016年1月1日至2018年2月28日的日度业务量数据，测试样本为2018 年3 月1 日至2019年至2月28日的日度业务量数据。

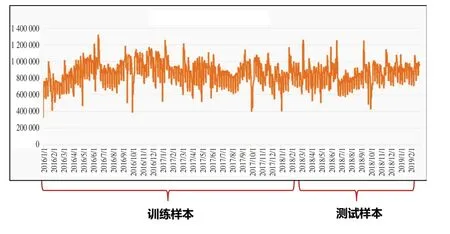
图2 原始序列时序图

3.1.1 平稳性检验。时间序列的初步检验是平稳性检验，若时间序列是非平稳的需将序列平稳化处理。平稳性检验有两种方法，一是通过观察原始时间序列时序图和自相关图等图检验，二是单位根检验法。本文运用单位根检验法（如图3所示）得出DF值为-3.602，是平稳序列。对样本进行正态分布检验和t检验，样本通过t检验但未通过正态分布检验，说明原始序列具有白噪声，为消除白噪声影响，对原始序列进行一阶差分，然后进行白噪声检验，得到p 值为0.279 1，大于0.05，未通过检验，继续进行二阶差分，白噪声检验的p 值约为0，小于0.05，通过白噪声检验。从图4 也可以看出二阶差分序列的噪声比一阶差分序列明显减少。

图3 原始序列的单位根检验及样本均数分布检验（左）与白噪声检验图（右）

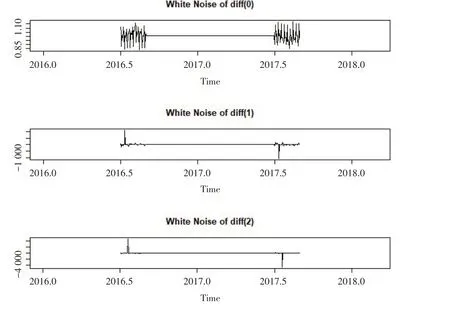
图4 原始序列（上）、一阶差分序列（中）、二阶差分序列（下）白噪声检验图

3.1.2 季节性分解。从图5的偏相关图发现原始序列存在周期性的季节波动，当滞后阶数为8,15,22时，偏自相关系数显著不为0，所以判定季节性周期S=7，对原始时间序列数据进行季节分解，分解为趋势项、季节项、随机扰动项，如图6所示。从图6可以看出趋势项波动最大，其次是季节项波动较大。季节性波动可以通过季节差分来消除季节影响，对季节序列进行单位根检验（如图7所示），DF值为-3.341 1，小于3，即季节序列是平稳的，但正态分布p值为0.21，大于0.05，即季节序列具有噪声影响；所以将季节序列进行一阶差分处理，对一阶差分的季节序列进行白噪声检验，p值为0.192 4，大于0.05，即一阶差分季节序列仍具有噪声影响；再对其进行二阶差分处理并对二阶差分季节序列进行白噪声检验，p值约为0，小于0.05，即二阶差分季节序列不存在白噪声影响。

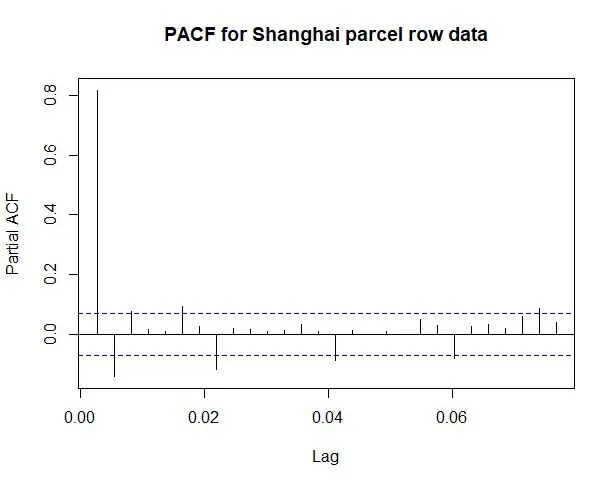
图5 原始序列偏自相关图

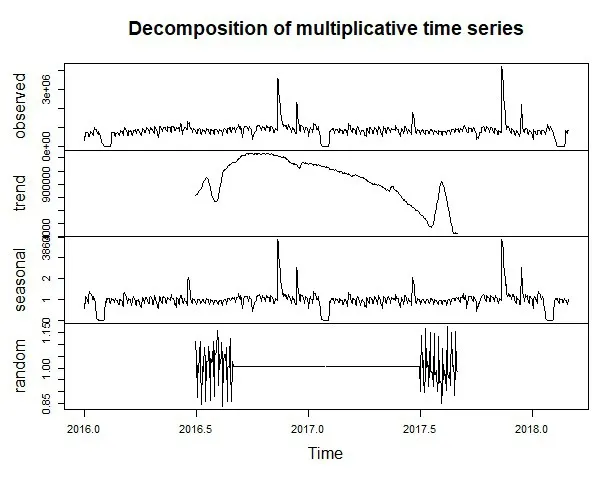
图6 季节分解图

图7 季节序列单位根检验（左）和季节差分序列白噪声检验（右）

3.2 模型识别与参数估计

由3.1.1中可知非季节二阶差分序列是平稳序列，所以对二阶差分后的时间序列数据进行自相关和偏相关分析，从图8中ACF图得出滑动平均模型参数q估计为1、2，从PACF图得出自回归模型参数p估计为13，d=2；从图9中的季节二阶差分的ACF图得出季节滑动平均模型参数Q估计为1、2，从PACF图中可知季节自回归模型参数P 估计为6，D=2。经过测试得出SARIMA(13,2,2)x(6,2,2)7是最佳模型（如图10所示）。

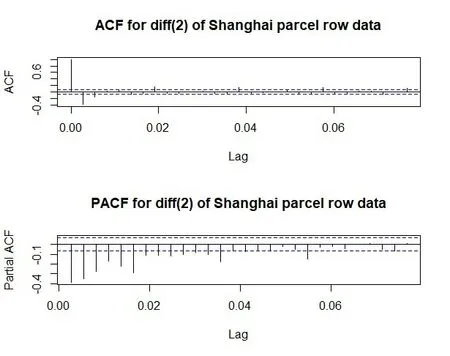
图8 二阶差分序列的自相关图（上）和偏相关图（下）

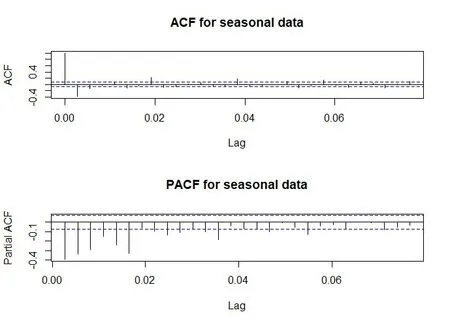
图9 季节二阶差分序列自相关图（上）和偏相关图（下）

图10 模型参数估计

3.3 模型检验

模型检验包括模型显著性检验和参数显著性检验。模型显著性检验是检验模型残差项是否为白噪声序列，从图11 残差自相关图可知t=0 时，acf=1,t 不为0 时，acf 都趋近于0，且残差白噪声检验的p 值显著大于0.05，接受原假设该拟合模型的残差序列是白噪声序列。从图11 可知模型参数通过参数显著性检验。

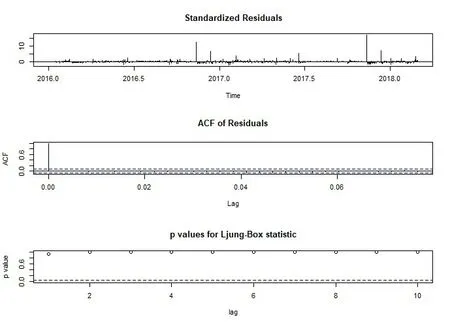
图11 模型残差白噪声检验图

3.4 模型优化

为提高模型的性能，本文分析研究SARIMA(13,2,2)(6,2,2)7模型中的残差项，对其进行优化，从图12观察得出模型残差数据y与SARIMA模型拟合值x之间存在相关关系。由于SARIMA 模型拟合值数据较大，不便与残差数据y 进行分析研究，因此对数化处理SARIMA模型拟合值，然后画出散点图（如图13所示），从散点图中观察到大多数点都聚集在一起，说明两者之间存在线性关系。对两者进行线性拟合，建立线性回归方程，拟合结果如图14所示，常数项系数为-1 222 843，一次项系数为90 179，系数对应的p值都小于0.05，通过显著性检验。最终预测模型为：SARIMA(13,2,2)x(6,2,2)7+(90 179*log(x)-1 222 843)。

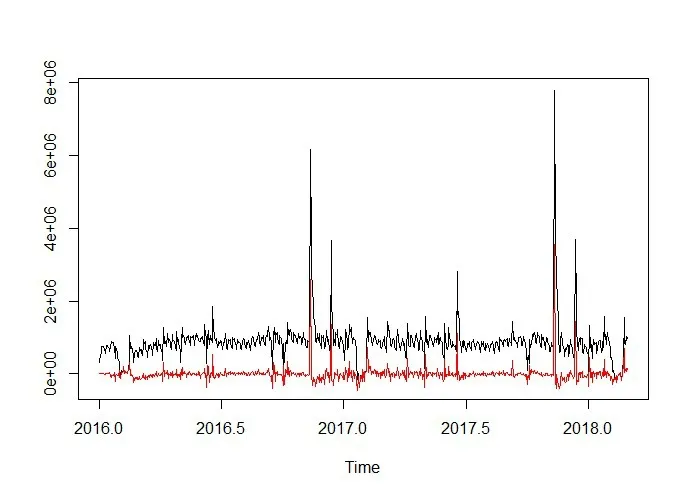
图12 模型残差与模型拟合值的分析图

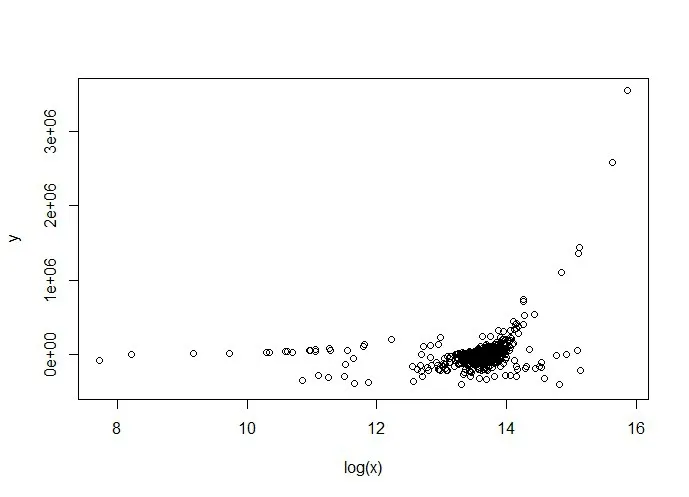
图13 模型残差与对数化处理拟合值的关系图

3.5 模型预测和评估

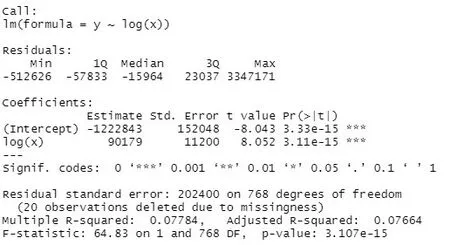
图14 线性拟合结果图

时间序列模型适用于短期预测，随着预测时间推迟，模型预测精确度下降，因此本文基于SARIMA(13,2,2)x(6,2,2)7+(90 179*log(x)-1 222 843)模型建立滑动窗口，滑动预测未来的业务量数据。滑动窗口模型是基于前n 天的样本数据预测未来第n+1,n+2,n+3天的业务量数据，当统计出第n+1天的实际业务量数据时，滑动窗口模型又基于前n+1天的样本数据预测未来第n+2,n+3,n+4天的业务量数据，以此类推，得到滑动窗口模型预测第一天的数据结果，如图15所示。根据预测业务量数据与实际业务量数据比较分析，对模型进行评估。本文采用平均绝对百分比误差方法评估模型，计算方式如下：

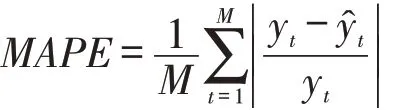
根据上式计算出平均绝对百分比误差为9.2%，但由于特殊节假日（如“618、双十一、双十二、中秋节、春节”等节日）时期电商平台的大促活动影响，特殊节假日的业务量预测误差较大，若不包含特殊节假日的预测误差，得出平均绝对百分比误差为7.0%，结果表明，该模型的预测效果较好。

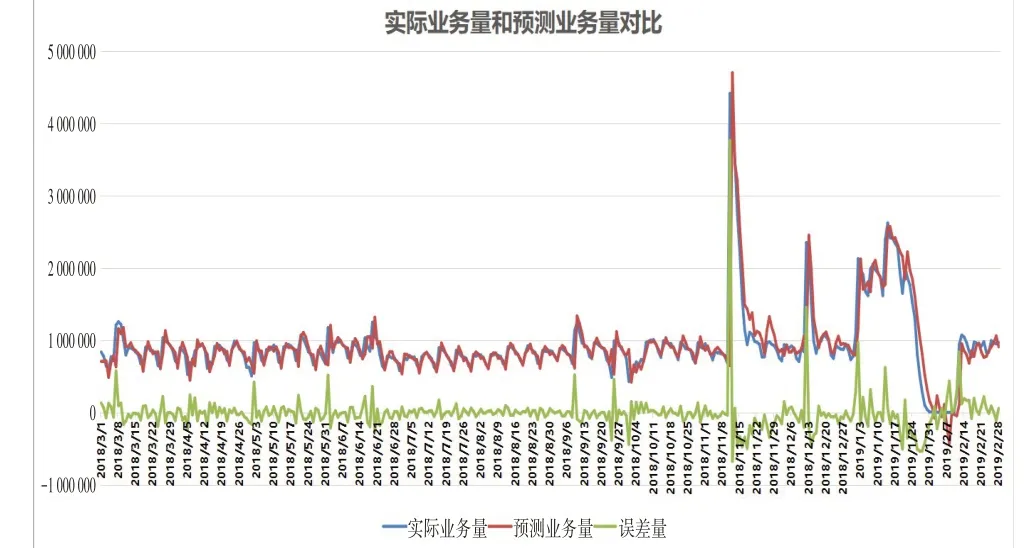
图15 实际业务量和预测业务量对比分析图

4 结论与不足

4.1 研究结论

本文通过分析发现，日度快递业务量数据既有增长趋势又有季节周期性的特点，运用时间序列分析方法建立SARIMA乘积模型，为提高模型精度对模型残差进行优化，又因SARIMA模型预测精确度随时间增长而降低，所以建立为期三天的滑动窗口模型预测日度业务量数据。从预测结果分析，模型预测业务量数据与实际业务量数据的平均误差为9.2%，若除去特殊节假日的预测误差，模型的平均误差为7.0%，预测误差在可接受范围内，所得结果对快递企业具有一定的参考意义。

4.2 研究不足

本文研究的不足包含以下三点：第一，本文建立的时间序列模型虽然考虑了增长趋势影响和季节周期性影响，但未考虑特殊节假日时期电商平台的大促活动影响，若将此因素影响纳入模型，模型性能将提高，预测精度也将提高。第二，本文运用时间序列方法建立SARIMA模型，模型的预测精度随预测时间推迟而降低，只适用于短期预测不适用于长期预测。第三，本文对快递业务量的预测仅采用了时间序列分析中的SARIMA模型，若同时采用多种研究方法建立多个模型进行预测，选取一个最优模型，模型拟合效果更好，预测精度更高。