LNG 绕管式换热器壳程两相降膜换热的数值模拟

董龙飞，刘 坤

（中国石油大学胜利学院油气工程学院，山东东营257061）

自2000 年以来，全球液化天然气需求年均增长6%，2016 年LNG 需求达到2.65×108t，中国、印度和新兴的进口国对LNG 进口增长做出了主要贡献[1]。为了改变能源结构、改善环境状态，早在2013年，国务院办公厅发布的《能源发展战略行动计划（2014-2020 年）》就明确提出，到2020 年，天然气占我国一次能源消费比重将达10% 以上[2]。然而，由于天然气具有密度小、体积大的特点，当直接对天然气进行输送时存在效率低、成本高的问题，因此为了便于运输，人们常常采用将天然气液化形成液化天然气的方式进行运输。

LNG 绕管式换热器[3-4]（Spiral-wound LNG heat exchangers）主要用于大型陆上天然气液化工厂和大型LNG-FPSO 工艺进行天然气液化，目前90%的大型液化装置选用了绕管式换热器。浮式LNG(简称FLNG）技术作为一种经济高效的深海天然气田开发模式，具有广泛的应用前景，但海上特殊的环境对FLNG 关键设备的工作性能提出更加苛刻的要求，绕管式换热器作为液化流程中的主要设备，它的投资占总投资的20%～30%[5]，并且绕管式换热器的换热及流动性能直接影响着其他设备的选型以及液化工艺的规模。但目前有关FLNG 关键设备涉及到海上晃动环境影响的深层次研究较为匮乏，而这些设备能否正常、高效的运行，是决定FLNG 装置能否在深海环境正常投产运行的关键因素。

当工质由上而下流经水平管时，随着入口流量的增大，管间流型会依次出现由滴状流到柱状流，再到片状流的流动模式变化[6]（见图1）。X.Hu 等[7]提出了扩展的管间流型，包括完全滴状流、滴一柱状流、完全柱状流、柱一片状流和完全片状流。

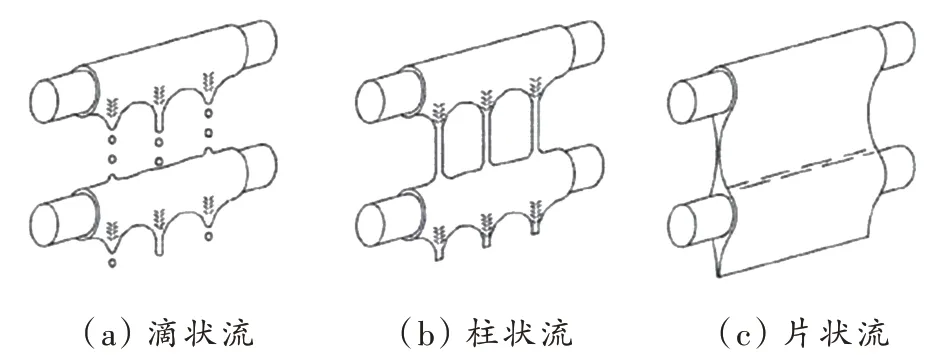
图1 理想的管间流动模式Fig.1 Ideal flow pattern between pipes

浦晖等[8]调查对比了国内外绕管式换热器供货技术的差异，发现了国内目前面临的技术难题，指出天然气预冷、液化、过冷等过程的热问题和温度关系难以被准确模拟与计算。吴志勇等[9]通过数值模拟得出了摩擦压力降变化规律以及换热管管缝处表面换热系数低的结论。同年，通过理论推导的方法给出了换热管缠绕层的各项参数计算公式以及流动间隙和流通面积计算公式的使用原则[10]。贾金才[11]对影响换热管传热特性的几何参数做了大量研究，得出管径越小、径向比越小、轴向比越大时换热效果越好的结论。

J.C.Messa 等[12]研究了不同缠绕角、轴向间距和径向间距对绕管式换热器壳侧换热的影响，结果表明结构对绕管式换热器的换热和压降影响显著。J.C.Ho 等[13-14]研究了绕管式换热器的换热模型，提出了不同工质和不同湿度条件下的换热模型，并实验验证了其正确性。J.C. Pacio 等[15]详细介绍了低温应用中的换热器热水力模型，包括集中参数模型、分布参数模型和流动发展模型，并指出了它们的不足，在模型计算过程中均忽略了换热过程中的压降和存在局部流混合的影响。B.G.Srbislav 等[16]对缠绕角度、径向间距、轴向间距等参数进行了分析，得出了关于Nu数的计算式：

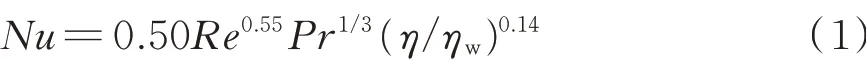
式中：Nu为努塞尔数，无量纲常数；Re为雷诺数，无量纲常数；Pr为普朗特数，无量纲常数；η为流体动力黏度，Pa⋅s；ηw为平均温度下流体动力黏度，Pa⋅s。

随着技术的革新，一些大规模、高成本的科研难关亟待人们攻克，正由于存在诸多问题，在现实生产中无法通过实验研究的方法解决各种难题，而数值模拟凭借其成本低廉、计算周期短、准确度高等优点被越来越多的人认可。现在，人们对绕管式换热器的研究尚不成熟，在壳侧冷剂单相对流换热、两相降膜换热、壳侧降膜流型变化以及结构参数对绕管式换热器的影响等方面仍然尚未得到解决。一方面，由于绕管式换热器在结构上与常规管壳式换热器存在较大差异，换热管是螺旋排列，因此不能用以往的经验关联式进行准确的描述；另一方面，开展新实验制造成本高，测量难度大，所以实验数据缺乏。因此，本文采用数值模拟的方法，通过与实验数据比对，提出了一种适合的计算模型，并对缠绕管外径、缠绕角、管间距等结构参数进行敏感性分析。

1 壳侧两相模型的建立

本文研究的气液相变问题主要考虑丙烷的蒸发。在进行数值模拟时，为使数学模型合理简化，做如下基本假设：（1）流体为不可压缩的牛顿流体。（2）各相的物性不随温度、压力等参数的变化而变化。

1.1 物理模型描述

选取的物理模型如图2 所示，壳侧冷剂在重力作用下，自喷淋入口喷淋至换热管，在换热管表面形成液膜，液膜沿换热管轴向和周向铺展运动，在换热管底部积聚，然后呈股流下。

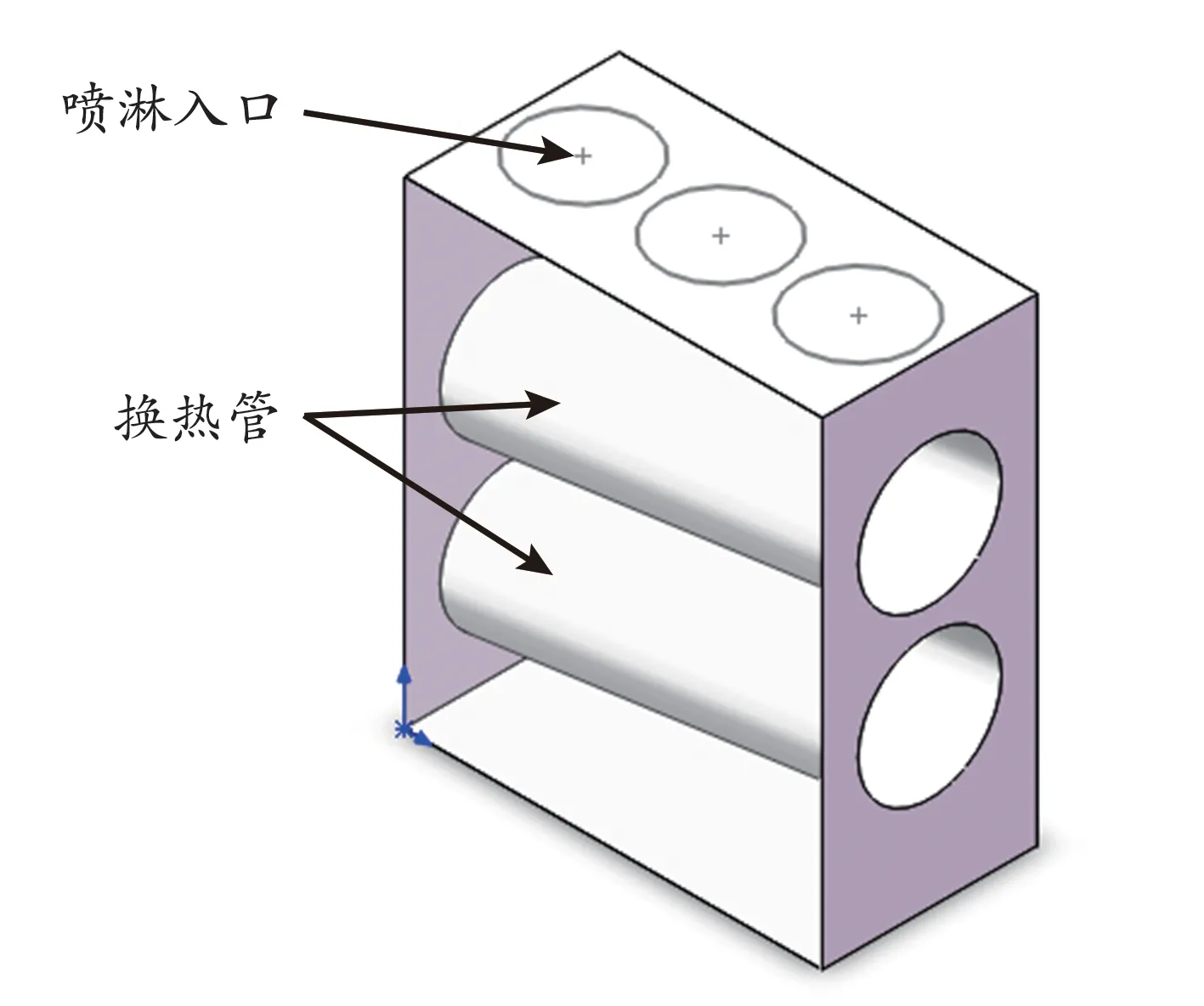
图2 三维数值模拟中的计算模型Fig.2 The model for three dimensional numerical simulation

1.2 控制方程的建立

流体在流动与换热过程中，要满足质量守恒、动量守恒和能量守恒三大守恒定律。而连续性方程、动量方程和能量方程是对三大守恒定律的数学描述。

1.2.1 连续性方程。

气相：

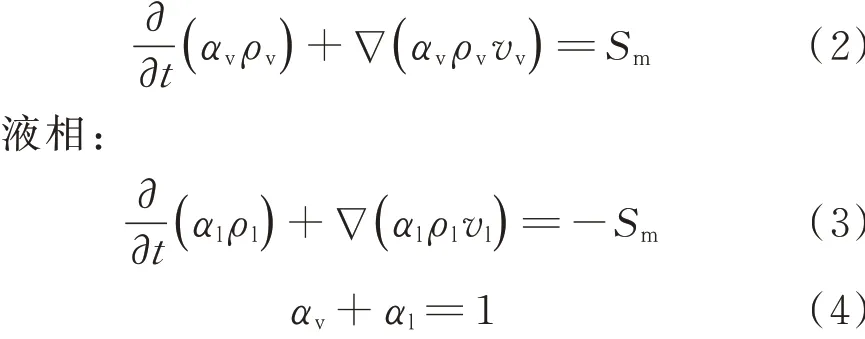
式中，αv和αl分别为气相和液相流体的体积分数，%；ρv和ρl分别为气相和液相流体的密度,kg/m3；Sm为传质质量源相，表示在换热过程中气相和液相之间的质量变化量,kg；vv和vl分别气相和液相流速，m/s。

传质质量源相Sm分为蒸发和冷凝两部分，当流体温度高于饱和温度时，流体会由液态变为气态，发生蒸发；当流体温度低于饱和温度时，流体会由气态变为液态，发生冷凝。

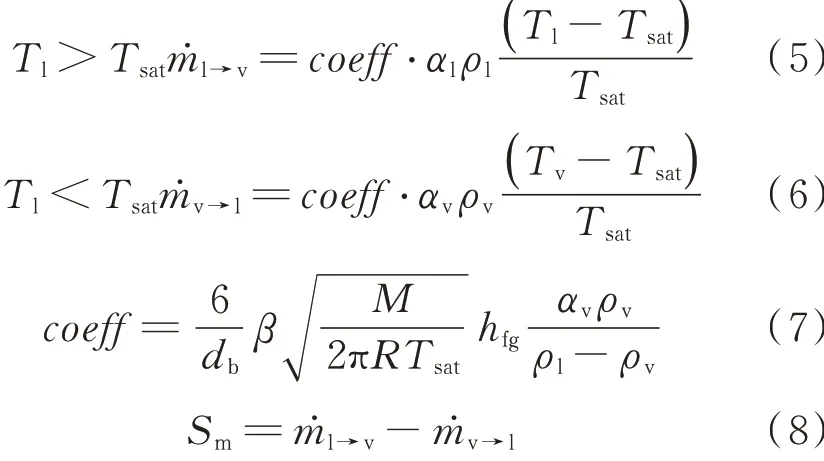
式中，Tl、Tv分别为液相和气相温度，K；Tsat为饱和温度，K；coeff为蒸发冷凝系数；β为气体的适应系数，β=1；db为气泡直径，m；hfg为汽化潜热，kJ/kg；M为质量流量，kg/s；R为缠绕管半径，m；ṁv→l、ṁl→v分别为气相变为液相和液相变为气相的质量，kg。

1.2.2 动量方程。

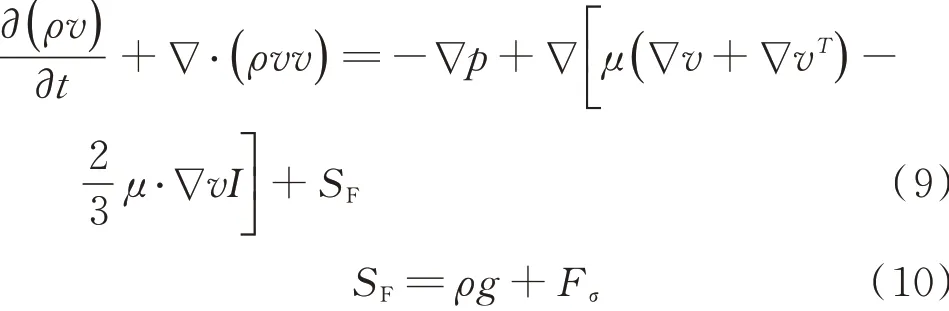
式中，T为流体温度，K；μ为动力黏度，Pa⋅s，I为动量，kg⋅m/s；SF为 广 义 体 积 力，N/m3；Fσ为 表 面 张力,N。

1.2.3 能量方程。

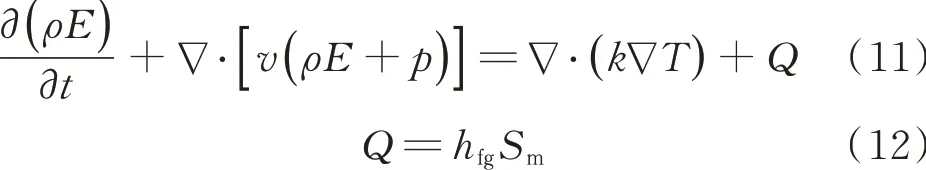
式中，E为内能，J/kg；p为压力，Pa；k为导热系数，W/(m⋅K）；Q为潜热源相，J。

1.3 网格划分和网格独立性

利用ICEM CFD 软件，采用结构化网格对计算模型进行网格划分，生成的网格如图3 所示。通过设置最大网格尺寸、网格层数等参数生成不同网格系统，具体方案如表1 所示。

在进行数值模拟时，以丙烷作为工质，利用VOF 多相流模型、蒸发传质模型以及连续表面张力模型（简称CSF）进行模拟计算。入口采用质量流量入口边界条件，出口采用自由出流出口边界条件，换热管采用恒定热流密度，外壁面采用绝热壁面条件。首先要进行独立性检验，图4 为不同网格数下换热系数与实验值的对比。由图4 可知，网格数量在14.5 万～36.6 万，换热系数变化很小，偏差均控制在0.5% 以内。为了加快计算速度，实际的数值计算都在网格数为14.5 万的条件下进行，其结果受网格数的影响较小。

图3 三维数值模拟中计算模型的网格划分Fig.3 The grid model for three dimensional numerical simulation

表1 网格划分方案Table 1 Mesh classification scheme

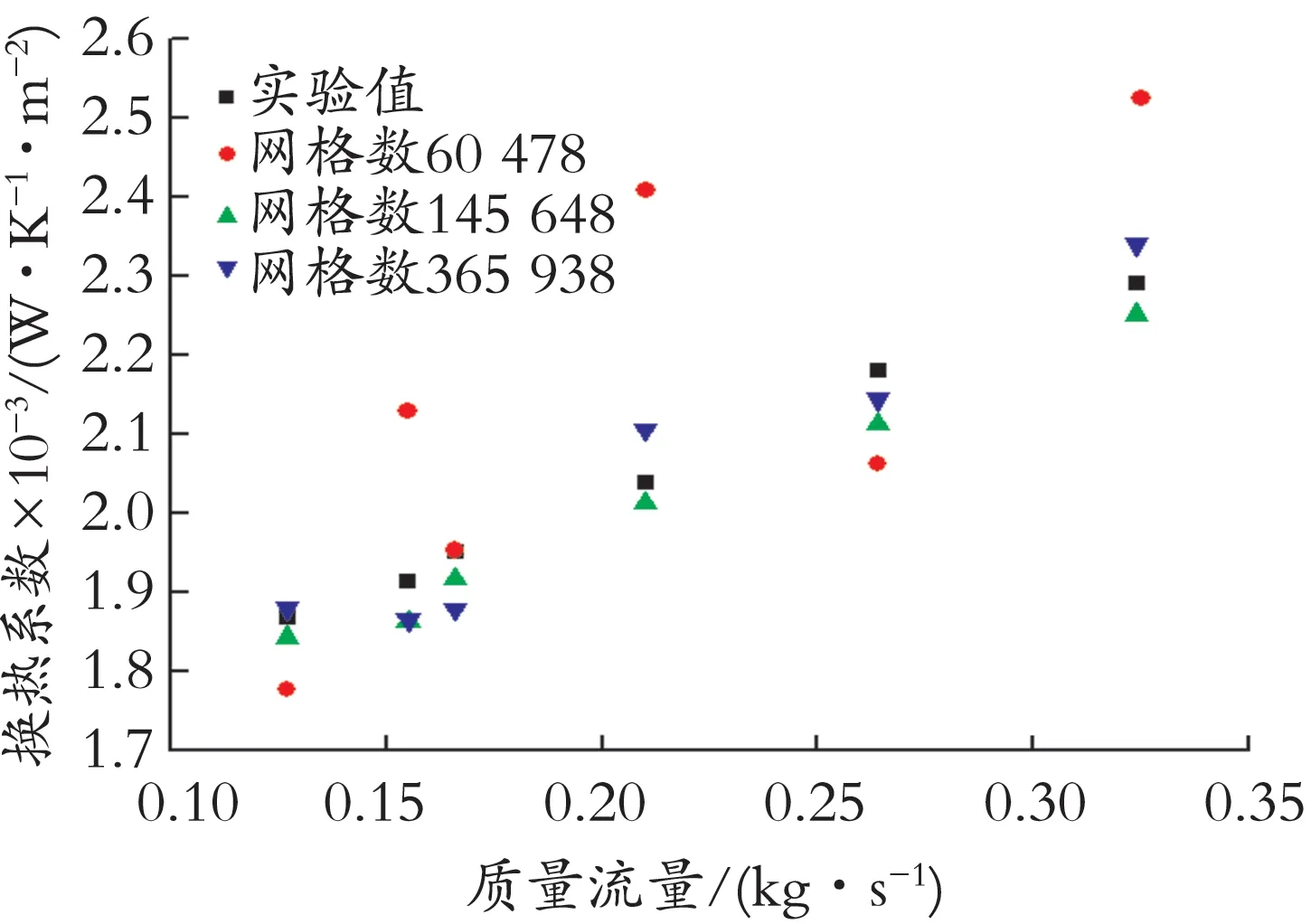
图4 独立性检验Fig.4 Test of independence

2 模拟与实验结果对比

为了验证数值模拟结果的正确性，本文的数值模拟结果与文献[17]中的以单一工质丙烷作为壳侧测试工质的两相降膜流动换热实验数据进行对比，实验过程中的压力、质量流量等条件见表2。

图5 为不同入口流量下数值模拟所测换热系数、实验所得换热系数和计算所得换热系数之间的对比。由图5 可以看出，通过数值模拟计算得到的换热系数与实验所得换热系数的偏差很小，均控制在6% 以内；将运用Neeraas 壳侧两相传热模型所得结果与实验值和模拟值进行对比，可以看出计算值与实验值和模拟值的匹配度很高，当质量流量为0.324 kg/s 时，计算值与模拟值的偏差达到最大，为6.62%。因此可以利用这个模型进行模拟计算。

表2 实验工况Table 2 Experimental condition

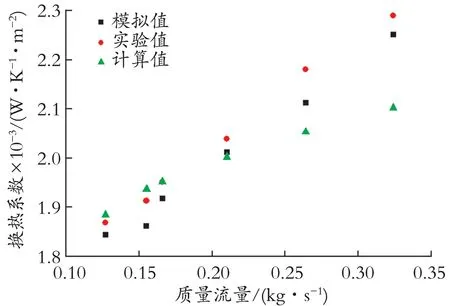
图5 不同入口流量下的换热系数Fig.5 Heat transfer coefficient with different mass flow rate inlet

图6 为换热器出口体积分数随入口质量流量的变化。由图6 可以看出，随着质量流量的增大，换热器出口处冷剂体积分数逐渐减小。这是由于随着质量流量的增大，壳侧冷剂吸收的热量更多的用于提高温度，属于显热换热，因此出口处冷剂体积分数随质量流量的增大而逐渐减小。

图6 不同质量流量下出口体积分数变化Fig.6 Gas phase volume fraction of outlet with different mass flow rate inlet

图7 为不同质量流量下，绕管式换热器轴向温度分布云图。由图7 可以看出，换热器右侧冷剂温度较高，左侧冷剂温度较低。这是由于换热管是倾斜管，当壳侧冷剂经分配器喷淋到换热管后，在换热管上呈液膜分布，在重力作用下，低温冷剂向换热管的左侧流动，导致左侧液膜的厚度大于右侧，因此吸收相同的热量，换热器右侧冷剂的温度要高于左侧冷剂的温度。

图7 不同质量流量下轴向温度云图Fig.7 Axial temperature cloud diagram with differentmass flow rate

3 模拟结果分析

3.1 缠绕角度对换热的影响

为了研究缠绕角度对绕管式换热器换热性能的影响，对缠绕角度为5°、8°、11°时换热器的换热特性进行了模拟分析。图8 为不同缠绕角度下，壳侧换热系数随质量流量的变化。

图8 不同缠绕角下换热系数随质量流量变化Fig.8 Heat transfer coefficient varies with mass flow rate of differen winding angle

从图8 中可以看出，不同缠绕角度下，壳侧换热系数随质量流量的变化趋势基本保持一致；在同一质量流量下，壳侧换热系数随换热管缠绕角度的增大而减小，以质量流量为0.127 kg/s 时为例，缠绕角度由5°增加到8°，换热系数降低了6.70%。当缠绕角度一定时，壳侧换热系数随质量流量的增大而增大，壳侧冷剂质量流量由0.127 kg/s 增加到0.324 kg/s，质量流量增加了2.5 倍，缠绕角为5°时的壳侧换热系数增加了15.15%，缠绕角为8°时的换热系数增加了18.13%，缠绕角为11°时的换热系数增加了10.79%。这是由于当缠绕角度增大时，换热管外表面的液膜在重力作用下会加速向换热管左侧流动，导致壳侧冷剂与换热管接触的时间变短，造成冷剂与换热管换热不充分，因此换热系数随缠绕角度的增大而减小。

3.2 管间距对换热的影响

为了研究管间距对绕管式换热器换热性能的影响，对管间距为14、17、20 mm 时换热器的换热特性进行了模拟分析。图9 为不同管间距下，壳侧换热系数随质量流量的变化。

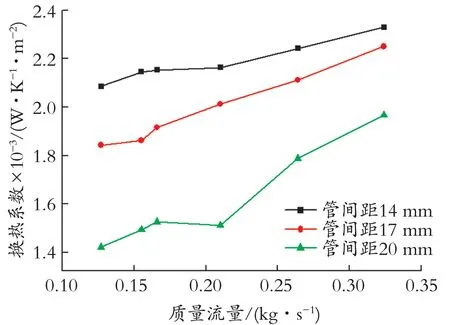
图9 不同管间距下换热系数随质量流量的变化Fig.9 Heat transfer coefficient varies with mass flow rate of differen longitudinal distance

从图9 中可以看出，不同管间距下，壳侧换热系数随质量流量的变化趋势基本保持一致，在同一质量流量下，壳侧换热系数随换热管间距的增大而减小；当换热管间距一定时，换热系数随质量流量的增大而增大。换热管间距由14 mm 增加到17 mm，壳侧换热系数降低了13.21%；质量流量增加2.5倍，管间距14 mm 时的换热系数提高了10.48%，管间距17 mm 时的换热系数提高了18.13%，管间距20 mm 时的换热系数提高了27.73%。这是由于当换热管间距增大时，壳侧冷剂由第一层换热管流到第二层换热管上时的速度增大，壳侧冷剂对换热管的冲击力变大，导致壳侧冷剂无法在换热管外表面形成稳定的液膜，使壳侧冷剂与换热管换热不充分，削弱了换热器的换热性能。

3.3 管外径对换热的影响

为了研究管外径对绕管式换热器换热性能的影响，对管外径为9、12、15 mm 时换热器的换热特性进行了模拟分析。图10 为不同换热管外径下，壳侧换热系数随质量流量的变化。

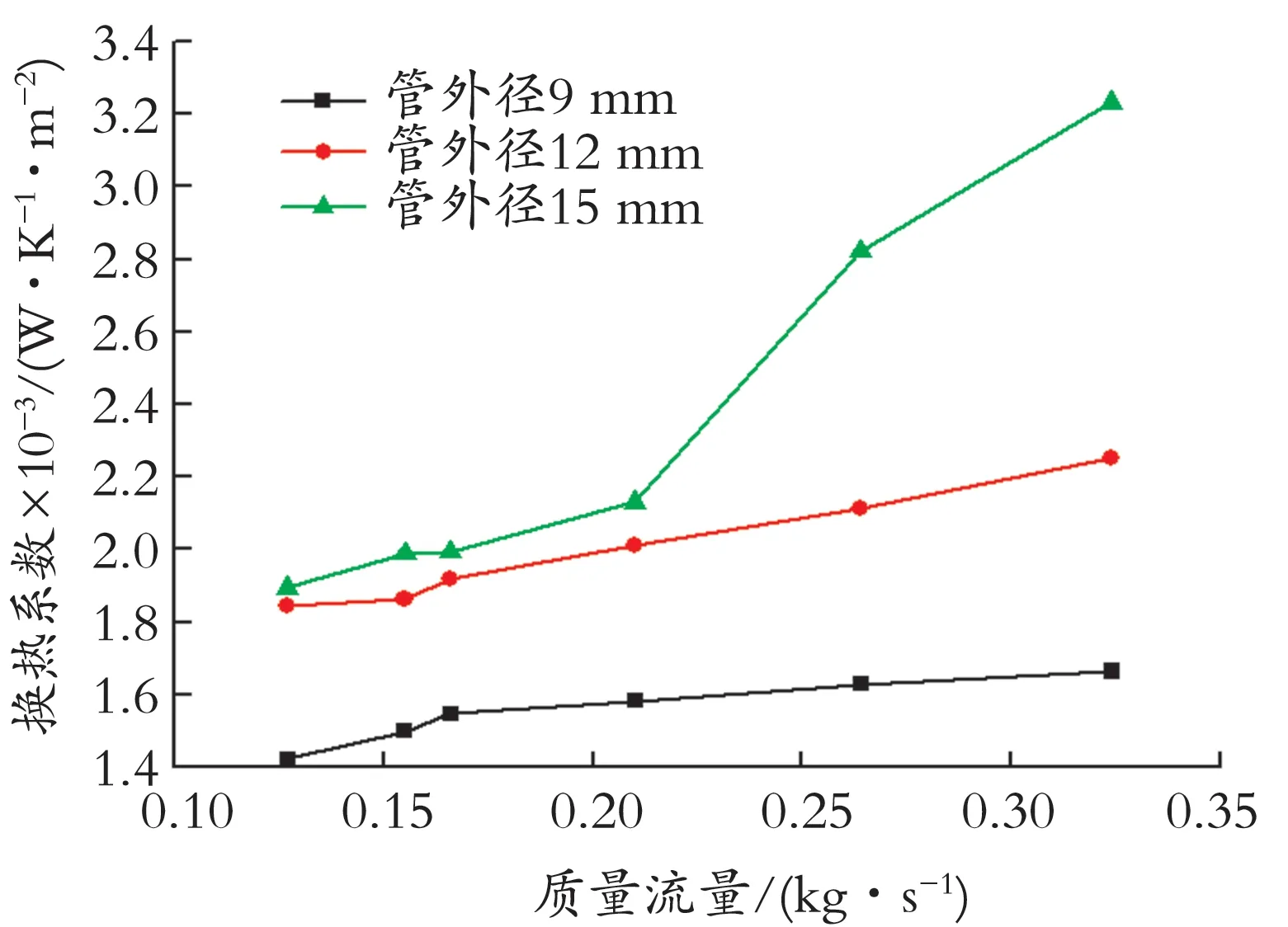
图10 不同换热管外径下换热系数随质量流量的变化Fig.10 Heat transfer coefficient varies with mass flow rate of differen outside tube diameter

从图10 中可以看出，不同换热管外径下，壳侧换热系数随质量流量的变化趋势基本保持一致，在同一质量流量下，壳侧换热系数随换热管外径的增大而减小；当换热管外径一定时，壳侧换热系数随质量流量的增大而增大。换热管外径由9 mm 增大到12 mm，壳侧换热系数增加了22.89%；质量流量增加了2.5 倍，换热管外径为9 mm 时的换热系数提高了14.55%，换热管外径为12 mm 时的换热系数提高了18.13%，换热管外径为15 mm 时的换热系数提高了41.39%。这是由于当换热管外径增大时，壳侧冷剂与换热管接触的表面积增大，使壳侧冷剂换热更加充分，提高了换热器的换热性能。

4 结 论

（1）在同一入口质量流量下，绕管式换热器壳侧换热系数随着换热管缠绕角的增大而减小，缠绕角度由5°增加到8°，换热系数降低了6.70%。

（2）在同一入口质量流量下，绕管式换热器壳侧换热系数随着换热管间距的增大而减小，换热管间距由14 mm 增加到17 mm，壳侧换热系数降低了13.21%。

（3）在同一入口质量流量下，绕管式换热器壳侧换热系数随着换热管外径的增大而增大，换热管外径由9 mm 增大到12 mm，壳侧换热系数增加了22.89%。