基于IMU阵列的标定方法
王 创,梁 伟,管 启,丁德锐
(上海理工大学 光电信息与计算机工程学院 上海 200093)
0 引言
微电子机械系统(MEMS)技术的发展使惯性传感器行业发生了革命性的变化,这使大规模生产超低成本惯性传感器成为可能。今天人们可以通过花费十几块钱就能够买到一个具有几平方毫米的惯性测量单元(IMU)。这些低成本小尺寸的IMU,使得构建大型的IMU阵列成为了可能,科研人员通过融合来自IMU阵列输出的数据信息,就能获得单个IMU不可比拟的性能,有关更多IMU阵列系统的具体内容请参见文献[1]。
低成本的MEMS 类型IMU的输出数据通常是未经校准补偿的[2-4]。集成电路在进行制造和封装过程中的缺陷,往往导致IMU的灵敏轴没有完全对齐,从而产生了轴失准误差和比例误差,这些误差项的存在导致了IMU输出数据的不准确。因此在融合来自IMU的信息前,应该对IMU进行校正补偿。在工业界,对IMU进行标定校准需要昂贵的机械校正平台[5-7]。在实验室级别的使用过程中,研究者们提出了不需要旋转机的简化标定方法[8-10]。这些方法利用重力矢量大小的先验知识来对未知参数进行估计,但仅限于单个IMU的校正。
近年来,由低成本的IMU组成的惯性传感器阵列受到越来越多的研究人员的关注。越来越多的研究人员把由低成本IMU组成的惯性传感器阵列应用在机器人的自主导航中。但是在使用由低成本IMU组成的惯性传感器阵列进行组合导航时,必须对惯性传感器阵列进行标定。在对惯性传感器阵列的标定的过程中不仅要对组成阵列的单个IMU进行标定,还要对惯性传感器阵列中IMU相对与标准坐标系的偏角进行标定。对单个IMU的校正建模已经非常成熟,但是对IMU阵列的校正模型研究比较少。
鉴于上述分析,本文首先对单个IMU的校正模型进行了分析和建模,然后在单个IMU校正模型的基础上,根据IMU阵列的特殊性建立了惯性传感器阵列的校正模型,该模型不仅包含了单个IMU的尺度、偏置和灵敏轴误差,还包含了惯性传感器阵列中IMU间的坐标系非对齐误差。由于惯性传感器阵列校正模型的非线性,本文构造了基于最小二乘法的代价函数,采用L-M算法来求解校正参数。在进行非线性求解的过程中需要足够多的外部激励,为此本文设计了一个具有20面的标准多面体,该20面体采用3D打印机获取。
1 IMU的误差模型
在理想情况下IMU的3轴加速度计和3轴陀螺仪使用了同一个正交三维坐标系。加速度计能感知不同方向上的加速度,而陀螺仪能测量围绕同一轴的角速度。不幸的是,由于IMU的封装过程的不准确,导致加速度坐标系和陀螺仪坐标系形成两个不同的非正交坐标系,见图1。
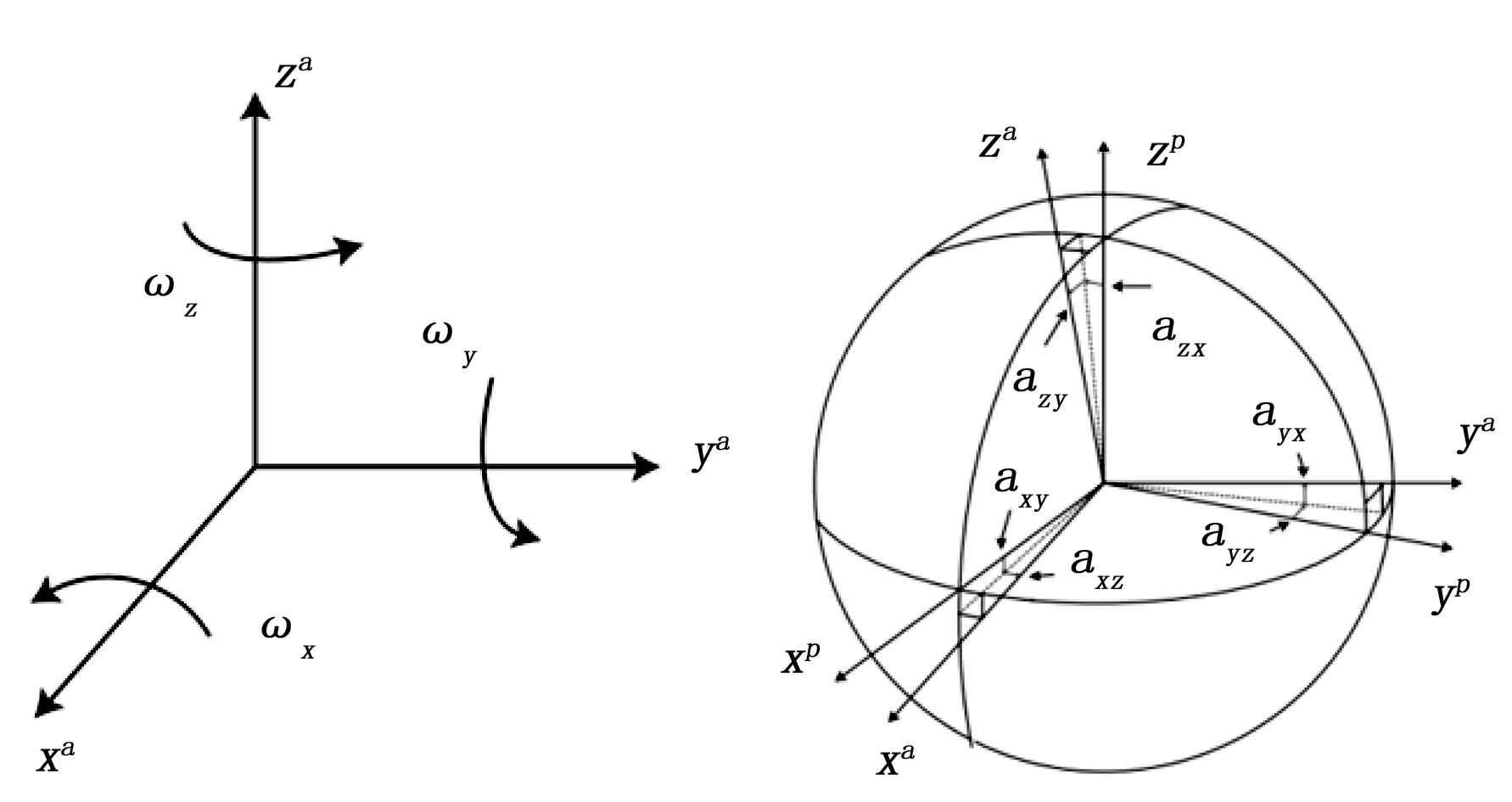
图1 IMU的轴失准误差
由于加速度计的3个灵敏轴和陀螺仪的3个灵敏轴与平台坐标轴的正交坐标系仅相差较小的角度,则在加速度计坐标中的比力测量可转化为平台坐标中的比力估计值
(1)
式中,sp表示平台坐标系下的加速计受的比力或陀螺仪的角速度,ss表示加速计坐标系下的比力或陀螺仪坐标系下的角速度。这里βij是加速度计或陀螺仪的第i个敏感轴绕第j个平台正交轴的微小旋转角。
理想的平台坐标系是正交的,通过使平台坐标轴的xp和加速度计坐标的xa灵敏轴重合,则平台坐标系的yp轴就会落在由xa和ya所成的平面上,那么公式(1)中角βxz、βxy和βyx变为零,加速度计坐标系和平台坐标的关系可以重新写为如下形式:
(2)
公式(1)中的β表示加速度计和陀螺仪通用的误差角,在公式(2)中用α表示适用于加速度计的情况。
如前所述,陀螺仪和加速度计的测量应该共用相同的参考系,由公式(2)可以得到陀螺仪的相关表达:
(3)
其中:wp和wg分别表示平台坐标系下的角速度和陀螺仪坐标系下的角速度,γij表示第i个陀螺仪敏感轴绕第j个平台轴的微小旋转角。
图1中的xa,ya,za表示加速度计的敏感轴,xp,yp,zp表示理想的正交轴,理想的正交轴和加速计灵敏轴的偏角可以表示为αxy,αxz,αyx,αyz,αzx,αzy。
MEMS类型的传感器输出的信息是和电压成比例的电信号,输出电压和作用在传感器灵敏度轴上物理量之间的关系由制造商的数据表给出,由于MEMS传感器的固有非线性导致输出电压和传感器测量的信号之间的真实比例不同,我们称此不同为刻度系数误差或者比例误差。此外,MEMS传感器的输出信号中通常会含有一个小小的偏差,具体的表现是,即使没有力作用在传感器上,传感器也会有非零的输出,称该非零输出为偏置。
对加速度计和陀螺仪都受到偏差和刻度系数误差进行如下的建模,其中刻度系数矩阵可以表示为:
(4)
偏置向量建模为:
(5)
针对上述的误差进行整体的数学建模,则完整的传感器误差模型可以用下式表示:
(6)
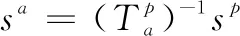
式(6)是对IMU的确定性误差的建模,该模型适用于所有的类型的IMU。但是MEMS类型的IMU不仅包含式(6)中包含的确定性误差,还包含由微电子结构特性造成的随机误差,随机误差主要是指MEMS类型IMU输出数据所包含的高斯白噪声和bias随机游走。本文仅仅对MEMS类型IMU阵列的确定性误差进行校正。
2 IMU阵列误差模型的构建
上一节对MEMS类型IMU的确定性误差进行了数学建模,本小节主要对IMU阵列的确定误差进行了数学模型的建立。IMU阵列所包含的误差不仅含有来自单个IMU的灵敏轴失准误差、偏置和刻度误差,还包括IMU阵列中不同IMU之间的非对齐误差。

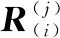
(7)
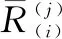
通过以上对IMU阵列独有的误差项的分析,本文在单个IMU确定性误差模型的基础上建立了IMU阵列的误差模型,在IMU阵列的误差模型中假设阵列中第i个加速度计的输出可以看做为第j个加速度计的输入和参数θ(j)的函数:
(8)
其中:

(9)

根据上述对参数的物理化解释,IMU阵列校正的参数模型表示如下:
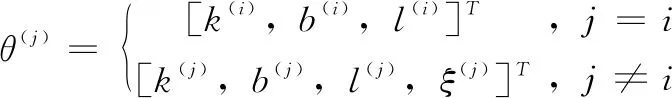
(10)
通过观察式(10)可以知道当j=i时,需要估计的参数就是单个IMU校正的参数,此时的IMU阵列校正模型退化成了单个IMU校正;当j≠i时,校正的参数是包含IMU阵列不同IMU间的非对齐误差。
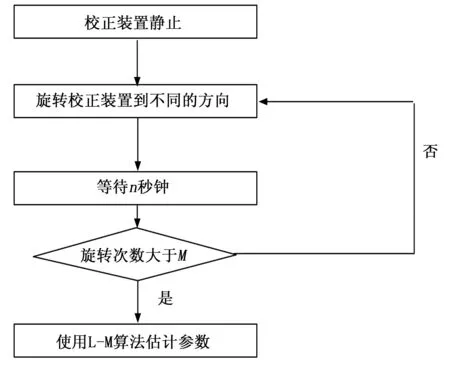
图1 IMU阵列校正流程
3 IMU阵列校正算法设计
在上一节中本文建立了IMU阵列的误差模型,通过公式(10)可以知道参数θ(j),j∈(1.M)包含了IMU阵列中单个IMU的轴失准误差、偏置、刻度误差和IMU阵列中IMU间的非对齐误差。通过建模分析可知校正的参数θ(j)的维度是15维。传统的六面标定法显然不能够为IMU阵列的校正提供如此多的校正激励,为此本文针对IMU阵列的校正设计了一个20面体校正装置,该校正装置能够为IMU阵列校正提供充足的外部激励。
在IMU阵列误差模型和本文所设计的校正装置基础上设计了如图1所示的校正方案。
3.1 IMU阵列校正函数的构建
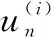
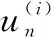
(11)
式中,c代表余弦函数,s代表正弦函数,φ表示偏航角、φ表示俯仰角、ψ表示翻滚角。
(12)
式中,φn和ψn分别表示第i个IMU的俯仰角和翻滚角。g是当地的重力加速度。
当IMU阵列静止时,输入矢量只有2自由度,而每个加速度计提供了一个在3中的重力矢量的估计值。这意味15维的校正参数通过式(12)的变换,减少了3维,只要能够在校正过程中提供至少12个非共面的方向激励,参数θ(j)就能够得到估计。
假设式(8)中的测量噪声为高斯白噪声,且不同IMU之间的噪声互不相关,通过求解如下代价函数最小值来得到参数θ(j)的最优估计:
(13)

(14)
式中,[a]k,k∈(x,y,z)表示向量a中的第k个元素。
3.2 IMU阵列校正装置的设计
通过上述的分析可以知道IMU阵列需要校正的参数有15维,经过公式(12)对输入的重力加速的简单变换,使IMU阵列的校正激励输入从15维降低到了12维。针对12维的校正激励输入,传统的六面标定法显然已经不能够满足IMU阵列的校正需求,这主要是由于六面法提供的激励不能够使方程校正方程(13)满秩,方程不满秩就会导致校正参数结果的不唯一,这显然不是IMU阵列参数校正需要的结果。
为了保证在IMU阵列校正的过程中获得充足的方向激励,本文设计了一个如图2所示的正20面球体。该球体是由20个平面组成,它能够提供20个不同方向的平面,每个平面都能为IMU阵列的校正提供方向上的激励。

图2 IMU阵列校正装置
多面体的提供的方向数量决定了校正的精度,精度和校正时间符合正相关的关系。因此在标定实验过程中,用户可以根据实际的需求来选取合适的校正方向数和静止时间。本文所设计的20面体另一个好处是它能够平均一些随机误差和一些未建模的误差。
4 IMU阵列校正试验
为了验证本文所提的校正方案的有效性,本文对如图3所示的IMU阵列进行了校正,该IMU阵列集成了来自Invensense的32个MPU-9250型IMU和一个来自Atmel的AT32UC3C2512微控制器。

图3 IMU阵列单元

由于选取的IMU阵列单元中的IMU个数太多,本文只对阵列中的前6个IMU的参数做了展示。表1中,刻度系数kx,ky,kz没有单位,加速度计偏置量bax,bay,baz的单位为m/s2,IMU的安装误差角lyz,lzy,lzx的单位为rad,坐标系对齐误差ξx,ξy,ξz的单位为rad,陀螺仪偏置量bgx,bgy,bgz的单位为rad/s。表1中编号为1的IMU所在的坐标系定义为IMU阵列的参考坐标系。即,编号为1的IMU没有估计IMU之间额外对齐误差。通过分析表1中的校正均值校正结果的量程值表明,校正结果的一致性。
为了说明校正参数的准确性,本文参考了Invensense公司的MPU-9250技术手册,并使用了第一个IMU估计参数的结果和官方所给的参数进行了比较,结果如表2和表3所示。

表1 数据表

IMUlzylzxξxξyξzbgxbgybgz1-0.003 66-0.005 34000-0.509 62-0.390 780.182 87622.23E-050.005 440.001 538-0.002 66-0.003 75-0.190 83-0.532 95-1.121 763-0.001 18-0.002 39-0.004 960.001 218-0.002 171.385 679-0.076 150.129 85240.002 520.000 8970.000 9610.001 83-0.005 22-0.699 93-0.462 8-0.407 5350.002 1450.003 183-0.002 690.002 1730.000 744-1.311 58-0.655 980.840 20860.008 1060.025 504 20.000 5810.002 468-0.007 394-0.183 961.006 5840.126 783

表2 加速度计比例因子误差
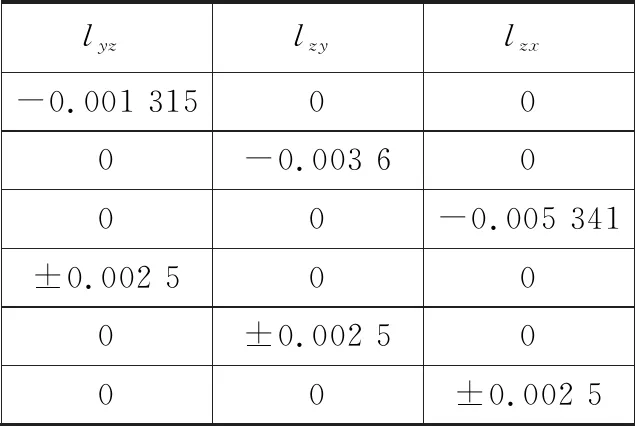
表3 敏感轴失准误差

表4 加速计和陀螺仪的偏置
表2和表3的左边是经过所提校正方案得到的校正结果,右边是MPU-9250技术手册提供的加速度计的比例因子误差和敏感轴失准误差的范围,由于MEMS类型的传感器受环境温度的影响,不同的校正环境的温度会导致不同的校正结果,但是两者的校正的数量级还在同一个级别,这证明了所提校正方法的有效性。
对于MEMS型的IMU,它的加速度计和陀螺仪的偏置是随机游走的,还不能针对长时间的偏置给出一个长时间的标定输出,表4仅仅给出了在室温为25 ℃的环境下,对加速计和陀螺仪的偏置的标定结果。
5 结束语
本文首先分析了单个IMU的确定性误差,并对单个IMU的确定性误差建立了数学模型。然后在单个IMU误差数学模型的基础上,考虑到IMU阵列的特殊性,设计了一套基于IMU阵列确定性误差的标定方案。该标定方案主要是利用当地的重力加速度作为校正过程的系统输入,并利用该输入构造了关于IMU阵列校正参数最小二乘问题,由于在求解过程中需要外接提供充足的方向激励,本文又设计了20面球体,如图2所示。该20面球体不仅能够为IMU阵列的校正提供充足的外部激励还能够平均一些随机误差和非建模的误差。为了测试标定的实验结果本文采用了由32个IMU组成的IMU阵列作为标定对象,标定结果见表一。把经过标定的结果和Invensense公司的MPU-9250技术手册所提供的标定结果进行了比较,结果表明本文所提的标定方案能够提供一个较好的标定结果。本文所提的标定方案不仅适合于IMU阵列的标定,同时也适合单个IMU的标定。

