基于状态观测的非脆弱跟踪控制器设计

程权成，崔宝影

（辽宁机电职业技术学院 华孚仪表学院，辽宁 丹东 118009）

0 引 言

在控制系统分析中，稳定性分析和跟踪性能分析是两类典型的分析方法，跟踪性能分析比稳定性分析更加复杂。跟踪控制是指通过设计控制器，在保证系统稳定的前提下，使系统的输出变量能够跟踪某一参考信号的输出变量。由于在控制器的设计过程中，并不是所有的状态变量都是可直接测量的，因此本文采用状态观测方法对状态变量进行观测，进而完成控制器的设计。刘玲等为了保证被控系统的跟踪控制性能，提出一种基于状态反馈的H∞跟踪控制器设计方法[1]；鹿竹叶等以火电机组机炉协调系统为研究对象，对闭环系统进行H2/H∞跟踪性能分析，并给出求解的LMI条件[2]，二者均假定状态变量是直接可测量的，但在实际系统模型中该假定并不是永远成立的。吴海东等结合LMI技术和鲁棒理论，研究了智能车轨迹跟踪控制方法提高了跟踪精度和鲁棒性，该研究分析了系统模型中的不确定性，但对于控制器的脆弱性没有进行深入探讨[3]。石振东等主要针对四旋翼无人机系统模型，研究了一种基于Lyapunov稳定性理论的H∞跟踪控制器[4]；孙宜标等采用LMI方法对直线伺服系统进行位移跟踪控制，并设计了求解控制器的条件[5]，二者均未考虑控制器中存在扰动时对跟踪性能的影响。Lin Chong等针对T-S模糊系统设计了基于观测器的跟踪控制器，应用LMI技术给出跟踪控制器的求解条件，并通过质量弹簧机械系统验证了设计方法的有效性，但其应用于线性连续时间系统时，求解过程过于复杂[6]。已有研究都是假定跟踪控制器是精确执行的，即未考虑非脆弱问题，然而，在实际系统模型中，由于A/D转换精度、元器件老化等因素，控制器参数往往并不是准确执行的，控制器参数微小的变化都会给系统带来严重的影响。本文利用非脆弱控制理论进行跟踪控制器求解条件的推导，即考虑跟踪控制器内部中存在的扰动，利用Lyapunov函数方法和LMI方法，设计跟踪控制器和观测器的存在条件，所研究的跟踪控制器及观测器综合采用H∞理论以及非脆弱理论，并通过数值仿真证明所提出方法可有效实现系统的跟踪性能和稳定性。

1 问题描述

考虑连续时间系统模型（1），将针对该系统模型进行基于状态观测器的跟踪控制器的设计。

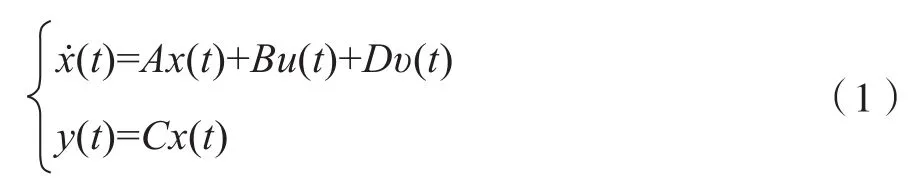
考虑参考模型如（2）所示，本文的控制目标是设计跟踪控制器使得y(t)能够跟踪yr(t)[6-8]。

实现跟踪控制目标的同时需要满足（3）所示的H∞输出跟踪控制性能指标[6-8]：

其中，χ(t)=y(t)-yr(t)，δ(t)=[υT(t)rT(t)]T，Q为正定的加权矩阵，γ为给定的性能衰减指标。

为实现该系统的跟踪控制问题，选取基于观测器的跟踪控制器模型为：

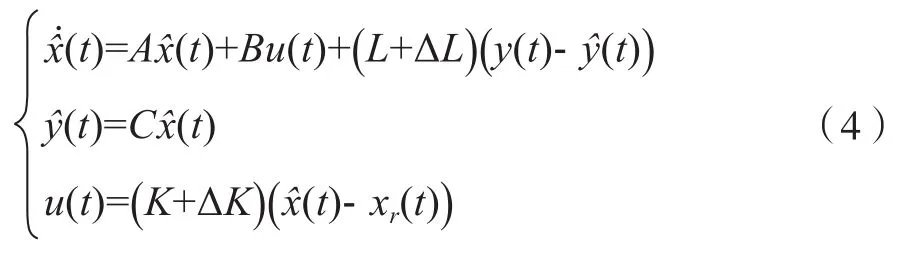
构建变量ϕ(t)=[κT(t)xT(t)xT r(t)]T和κ(t)=x(t)-(t)，结合（1）、 （2）和（4），可构建闭环系统模型（5）：

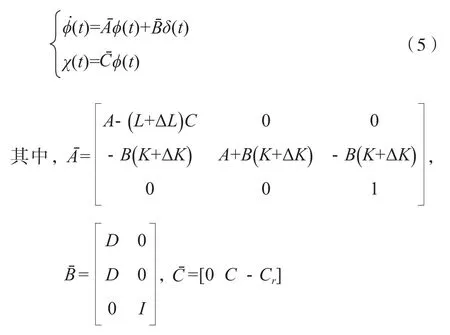
设计的主要任务是求解计算非脆弱H∞跟踪控制器K及观测器L，使（5）满足当δ(t)=0时是稳定的，同时存在γ＞0，使得性能指标（3）成立。

引理1和引理2将在本文结论的推导过程中起到重要作用。

引理1[9-11]：对于矩阵不等式条件（6）和不等式条件（7）是等价的。

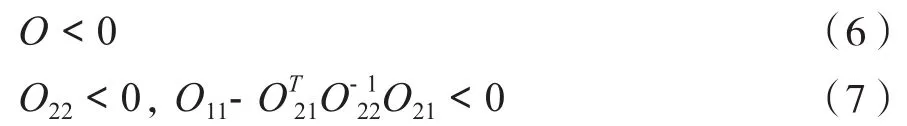
引理2[12]：对于给定适当维数的实矩阵X=XT,H,E, ΔTΔ≤I，可以得出结论，存在任意的常数λ＞0，使其满足下面的不等式关系：

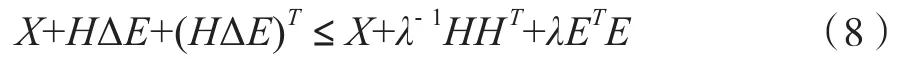
2 非脆弱跟踪器设计

利用LMI技术，推导非脆弱H∞跟踪控制器的LMI条件，该条件可通过Matlab软件求解。

定理1 针对闭环系统模型（5），若存在矩阵G1,J,F,G3,H以及常数ε1＞0,ε2＞0和γ＞0使得（9）成立：

证明：Lyapunov函数

由于G＞0，可知ρ(0)=0，且ρ(∞)＞0，因此， （11）成立。

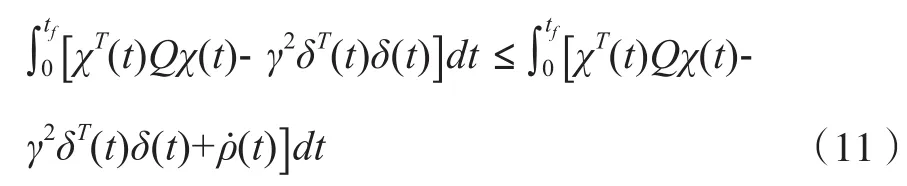
因此，如果（12）成立，那么闭环系统模型（5）的H∞跟踪性能就能保证。

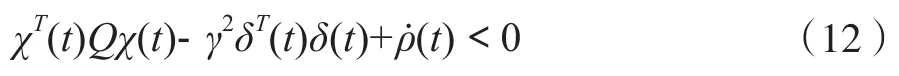
将χ(t)和δ(t)的定义代入（12），可得：

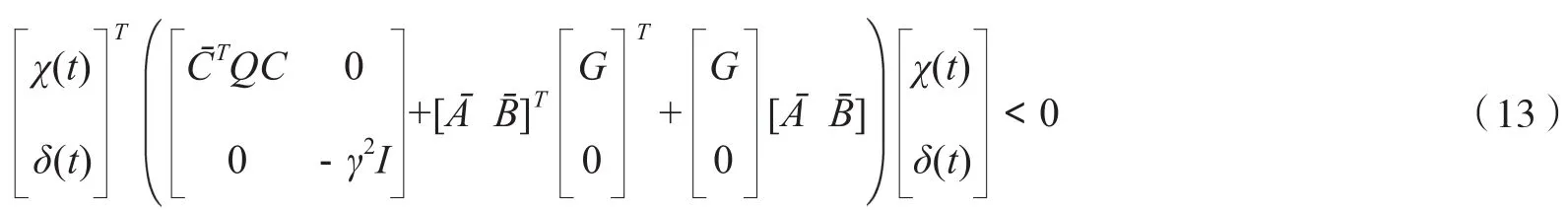
如果（14）成立，那么（13）成立。

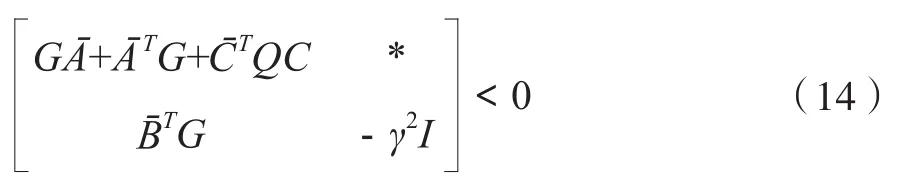
将引理1应用于（14），可得（15）。

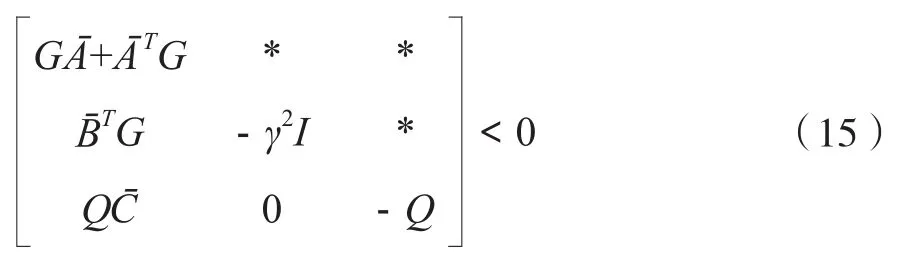
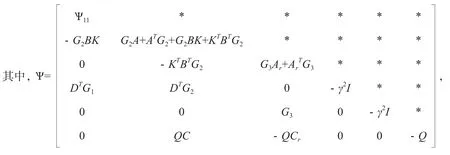
3 仿真实例

为进一步证明所设计基于观测器的H∞非脆弱跟踪控制器设计方法的有效性，设计仿真实例进行验证。选择系统的系数阵和外部干扰υ(t)如下：

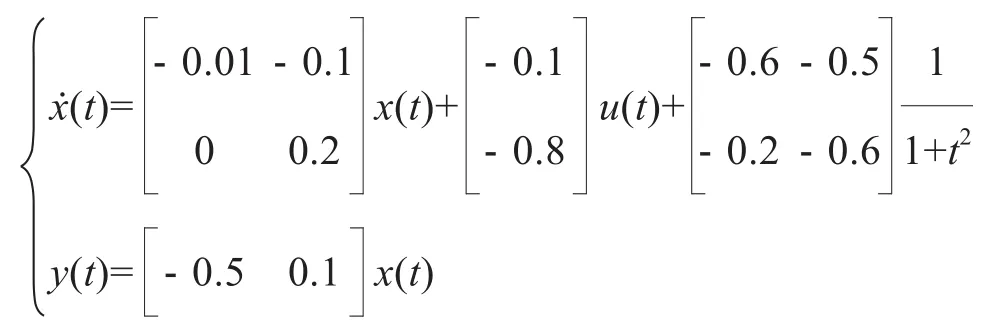
假定参考模型参数如下：

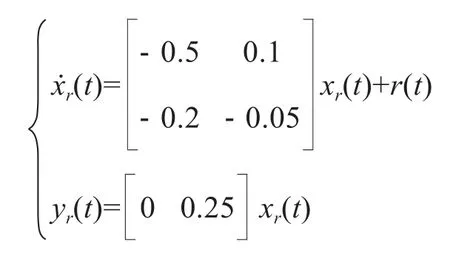
使用Matlab软件的M文件编写定理中阐述的非脆弱H∞跟踪控制器的LMI程序，当γ2=2.1时，求解出的跟踪控制器增益参数为：

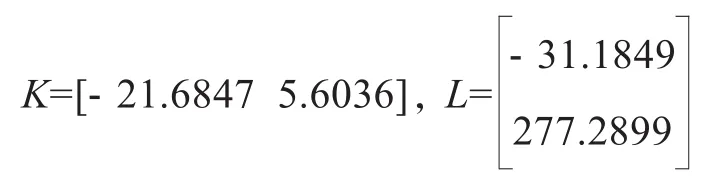
仿真过程中假设观测器和跟踪控制器中的参数增益不是精确可执行的，存在扰动的形式为ΔK=[0.1 0.2]*cos(t)*0.6和ΔL=[-0.7 0.01]*cos(t)*0.03。参考输入信号r(t)选择两种形式，形式1为：

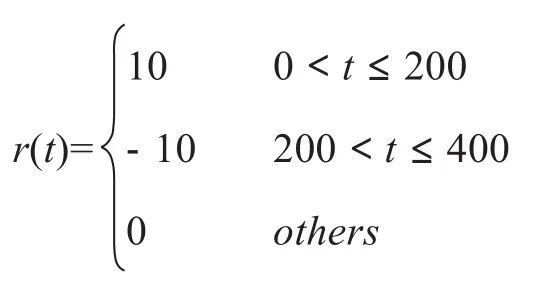
形式2为：r(t)=10+sin(0.05t)

对两种形式分别进行仿真。

使用Matlab软件的Simulink仿真功能进行基于观测器的非脆弱H∞跟踪控制器的稳定性和跟踪性能的分析，针对两种不同的参考输入信号r(t)，可仿真出闭环系统（5）的输出状态y(t)和参考模型输出变量yr(t)变化曲线如图1和图2所示。可见，所设计的跟踪控制器和观测器在存在内部扰动的情况下仍然能够实现对参考信号的跟踪，且当r(t)=0时，闭环系统（5）的输出状态y(t)也为0。因此，闭环系统（5）同时满足了跟踪控制性能和稳定性能，所设计的控制器是有效的。

若不进行非脆弱控制理论进行分析，则当跟踪控制器和状态观测器中存在干扰ΔK和ΔL时，针对两种不同的参考输入信号r(t)，闭环系统（5）的输出状态y(t)和参考模型输出变量yr(t)变化曲线如图3和图4所示。可见，不进行非脆弱设计，则存在干扰ΔK和ΔL时，虽然也可以实现信号的跟踪，但跟踪性能不及图1所示状态优越，尤其当参考输入信号r(t)为形式2时，y(t)与yr(t)的幅值与相位偏差均很严重。

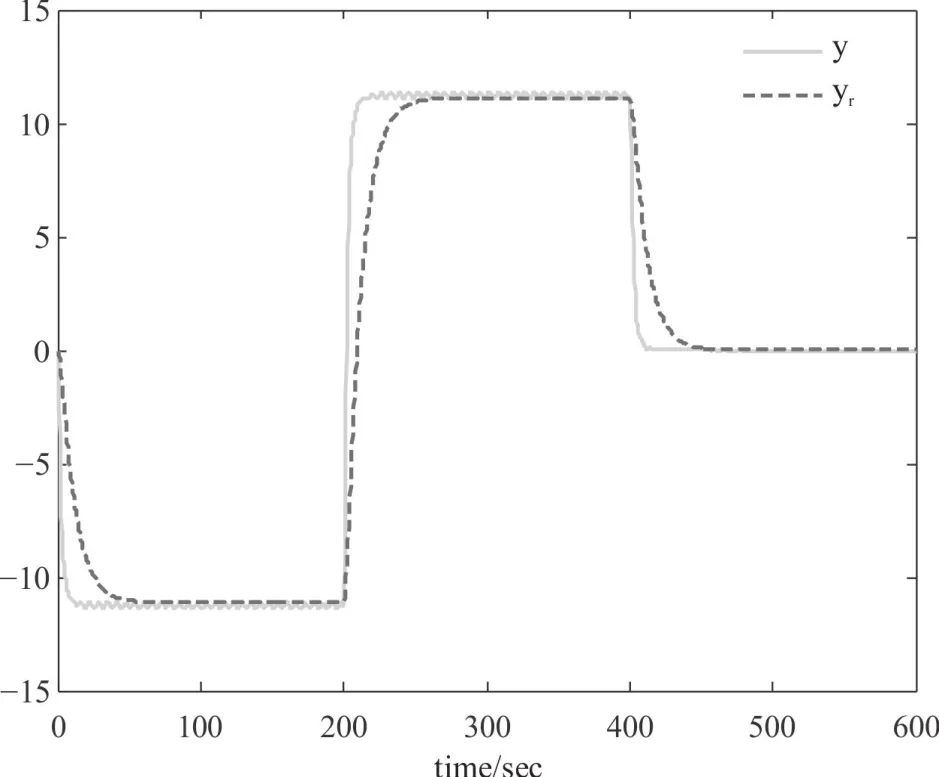
图1 闭环系统输出y(t)和参考模型输出yr(t)响应曲线（r(t)为形式1）

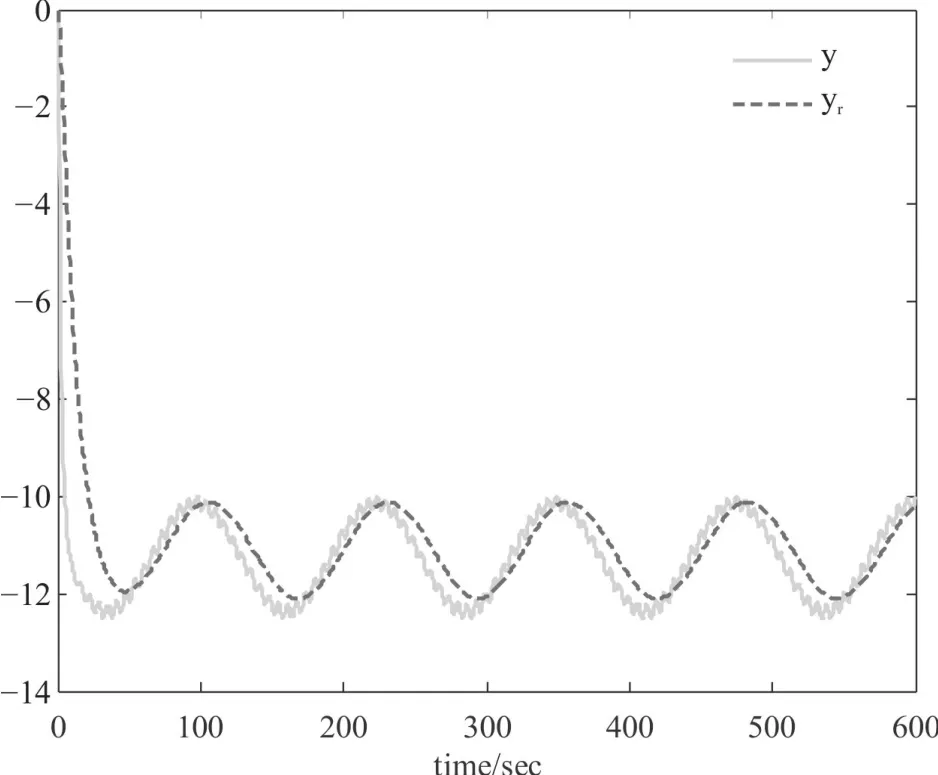
图2 闭环系统输出y(t)和参考模型输出yr(t)响应曲线（r(t)为形式2）

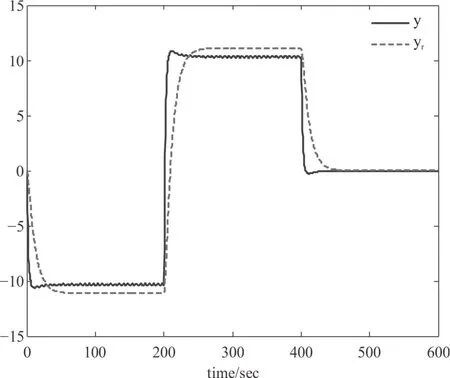
图3 未进行非脆弱设计的闭环系统输出y(t)和参考模型输出yr(t)响应曲线（r(t)为形式1）

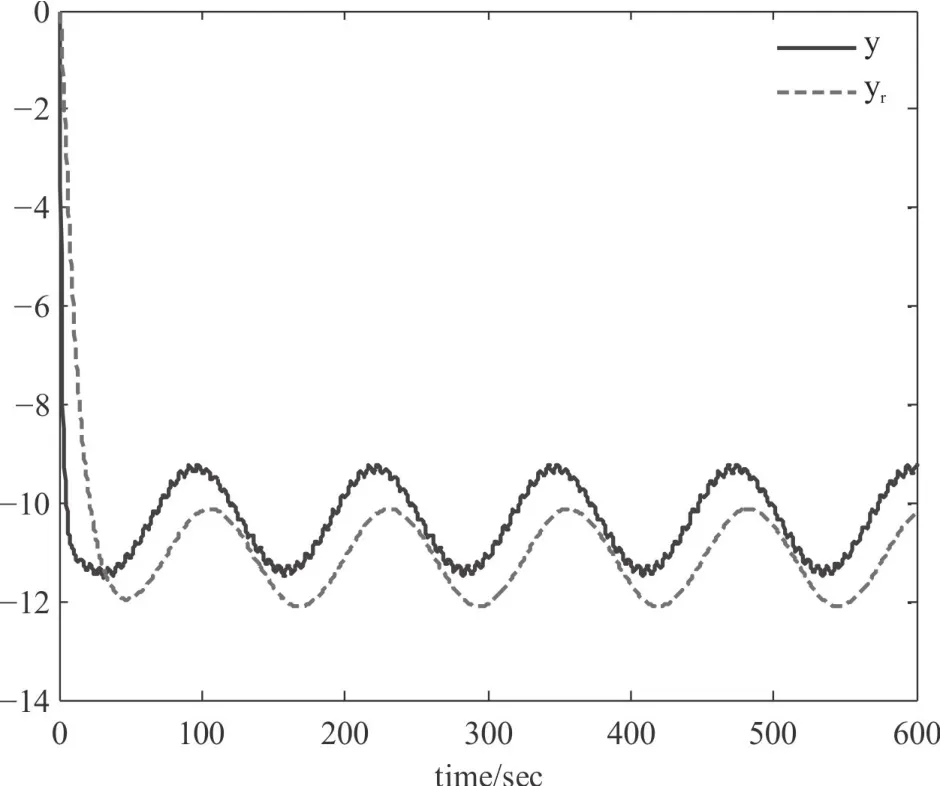
图4 未进行非脆弱设计的闭环系统输出y(t)和参考模型输出yr(t)响应曲线（r(t)为形式2）

针对两种不同的参考输入信号r(t)，跟踪误差响应曲线如图5和图6所示，e1为进行非脆弱设计时的跟踪误差响应，e2为未进行非脆弱设计时的跟踪误差响应，可见在任何时刻e1均比e2更趋近于0，即非脆弱设计后的跟踪误差小于传统控制器的跟踪误差。因此，可以得出结论，进行非脆弱设计后的跟踪控制系统，其跟踪控制性能比传统控制器系统更加优越。

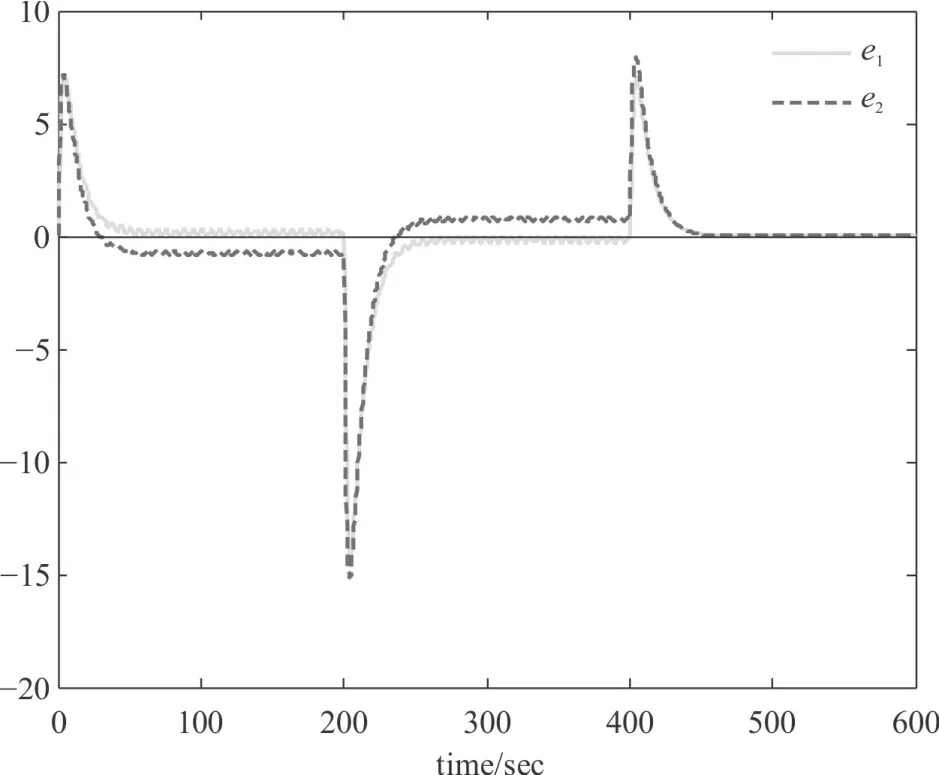
图5 跟踪误差响应曲线（r(t)为形式1）

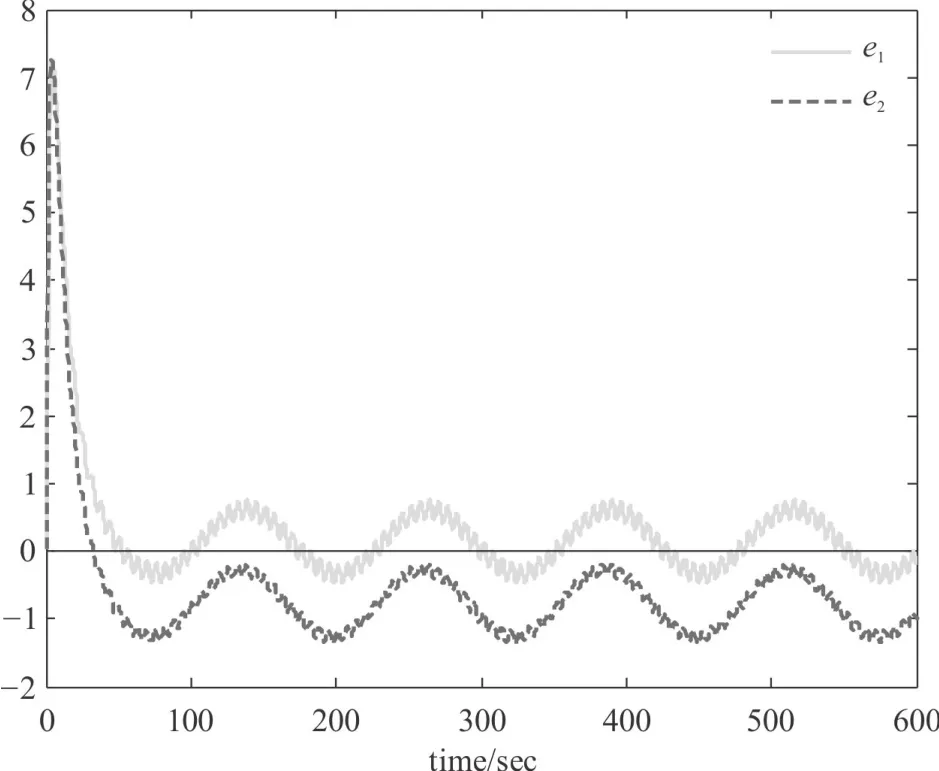
图6 跟踪误差响应曲线（r(t)为形式2）

4 结 论

本文构建了一种针对连续时间系统的非脆弱状态观测H∞跟踪控制器求解方法，采用Lyapunov稳定性理论方法，推导实现跟踪控制性能的不等式存在条件，通过有效的不等式变换技术得到了跟踪控制器的LMI存在条件。该条件可通过Matlab软件中的LMI Toolbox工具包计算求解。利用Simulink仿真技术对所设计的闭环系统进行仿真分析，根据输出响应曲线可以得出结论：即使当观测器和跟踪控制器中均存在干扰时仍然能实现输出状态的跟踪性能，且当跟踪参考信号输入为零时，系统的输出收敛于零，因此同时保证了跟踪性和稳定性。研究将非脆弱设计理论引入到跟踪控制器的应用中，增强了理论的应用性。