日常动态货物列车开行方案优化研究

李晟东，吕红霞,c，吕苗苗,c，徐长安，倪少权,c

(西南交通大学a.交通运输与物流学院；b.全国铁路列车运行图编制研发培训中心；c.综合交通运输智能化国家地方联合工程实验室，成都610031)

0 引 言

编组计划、列车运行图等运输计划根据中长期的货流预测数据编制得到，是一种静态计划，主要在宏观层面确定车流的组织方式.在铁路日常运营中，货流波动较大，运输组织根据“按流行车”原则，使实际货物列车的开行与计划的列车开行存在一定的出入.为使运输组织符合日常货流动态变化，有必要构建日常动态货物列车开行方案.

我国与以北美为代表的国外铁路在对货物列车开行方案的研究对象和范围界定上有较大区别.我国货物列车开行方案一般等同于列车编组计划[1-3]，国外货物列车大多为分组列车，其开行方案主要包括编组去向方案(blocking plan)，编组去向分配方案(block-to-train plan or makeup plan)，列车运营方案(train routing plan)[4-7].国内外关于开行方案的研究大多在中长期层面进行编制，该层面基于预测需求，主要确定列车开行的始发终到站、开行频率和编组内容.少部分研究[8-9]，以1 周为决策期的短期层面对开行方案进行编制，在确定列车开行始发终到站、开行频率、编组内容的基础上，进一步确定列车开行时间.在1周层面的计划编制中，虽然基于短期需求数据相较于中长期数据更为准确，但仍然是一种预测数据，与实际需求数据存在差异；其次，得到的开行时间确定了货物列车在1 周内的哪一天开行，相对于日常运营层面而言，其精度仍较为粗略.

日常动态货物列车开行方案，是以1 d为决策期，在编组计划、运行图等基本运输计划的基础上，根据日常动态车流，确定决策日货物列车开行的始发终到站、开行数量、编组内容，以及开行时段.因此，本文提出的日常动态货物列车开行方案进一步确定了决策日内，列车的开行时段.其次，既有研究在编制开行方案时，通常从运输企业生产效益出发，较少顾及货物实际运输需求，本文基于日常实际动态车流，考虑运到期限等货物运输需求.

1 问题分析

1.1 动态车流

动态车流指决策日路网中实际车流，由决策日当日新产生的车流和之前决策日产生并在当日在途的车流两部分组成.决策日新产生的车流，若在当前决策日内不能到达终到站，则当下一决策日到来，该车流成为在途车流.

以货物运到期限作为车流的时间窗，故车流i在途中任一车站s的运到时限(时间窗)为

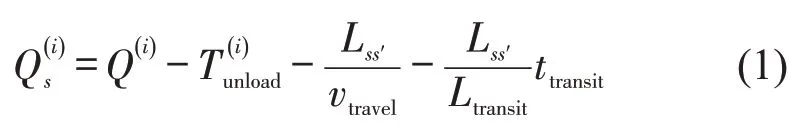
式中：Q(i)——车流i所装运货物的运到期限；

——车流i在其终到站的卸车时间；

Lss′——车站s与车流i终到站s′之间的里程(km)；

vtravel——货物列车平均旅行速度(km/h)；

Ltransit——货车平均中转距离(km)；

ttransit——车辆在技术站的平均中转停留时间(h).

以上相关数据可由《全国铁路统计资料汇编》查询得到.

引入车流到达违反时间窗的延误费用，即

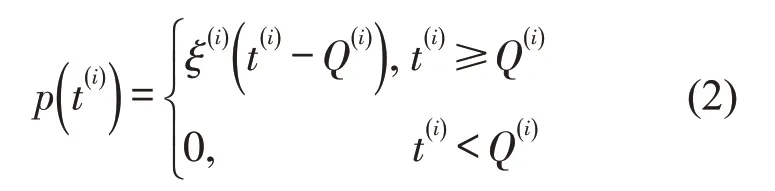
t(i)——车流i到达目的站的时间；

ξ(i)——延误惩罚系数.

1.2 列车服务网络

为描述列车运行过程，提出基于运行图等基本计划，构建货物列车服务时空网络.构建核心思想为：首先，将技术站等具有始发终到列车能力的车站视为车站集合对象，并获取相应的编组计划、运行图等；其次，将决策日离散为连续的时段，并将车站按时段进行扩展复制为服务网络节点；第三，基本运行图中，若在某一车站的某一时段内有列车始发，并终到另一车站的另一时段，则在相应的服务网络节点间构建有向的列车服务弧；第四，对于目标决策日，将同一车站的连续服务网络节点用有向的车站停留弧进行连接，用以表示改编车流在站的停留；最后，构建周期跨越弧，用以表示之前决策日出发，并在目标决策日到达的列车服务，周期跨越弧的构建，使开行方案得以实现每日滚动编制.一个简单列车服务时空网络如图1所示.

2 数学模型

2.1 边界假设

(1)铁路系统运输能力供应大于运输能力需求，保证决策日所有车流都能够被输送.

(2)车流径路已知，并且同一始发终到的不同支车流的径路是相同的.

(3)不考虑车流的树形改编策略.松弛树形改编策略，能够更加灵活地编组列车，防止车流为等待集结而导致在站停留时间过长.

(4)假定所有货物列车都为单组列车.

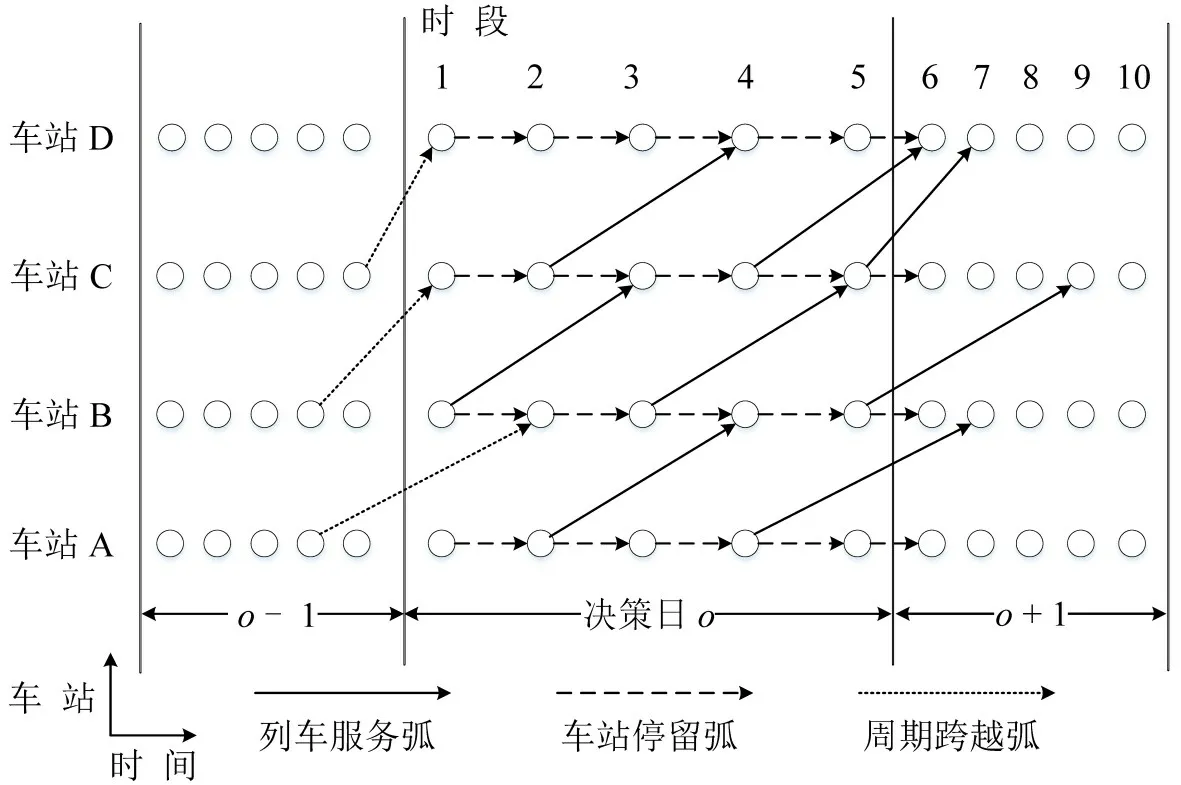
图1 列车服务时空网络Fig.1 Train service time-space network

2.2 符号描述

(1)集 合.

G——列车服务时空网络；

S——服务网络中车站集合，由技术站等具有列车始发终到能力的车站组成，车站索引为s；

A——服务网络中列车服务弧集合，服务弧索引为a；

F——车流集合，车流索引为i；

F(1)——决策日内新产生的车流集合；

F(2)——之前决策日内产生，在目标决策日到达，并将继续进行运输的在途车流集合；

S(i)——车流i径路上的车站集合；

δ+(s)——服务网络中s站发出的所有服务弧集合；

δ-(s)——服务网络中到达s站的所有服务弧集合.

(2)参数.

——车流i在流经弧a时的单位费用；

mi——车流i对应的货车数量；

oi，di——分别为车流i径路上的始发站、终到站；

γa——弧a开行单位列车的运营成本；

——0-1 常量，表示当弧a在车流i的径路上时，取值为1，否则为0；

——弧a相应的单位列车最大编成辆数；

——弧a相应的单位列车最小编成辆数；

——弧a对应的最大货物列车开行数量；

——弧a所对应的出发时段；

——弧a所对应的到达时段；

——车站s的最大有调中转作业时间；

——车站s的最小有调中转作业时间；

——本站装车完毕后新产生的车流，车站规定最大在站停留时间；

——本站装车完毕后新产生的车流，编组出发所需的最小在站停留时间，主要包括编组、集结和出发作业时间；

g——单位时段所对应的时长，单位通常为min；

——集合F(1)中的车流i在其始发站可以开始编入列车的初始时段，即装车完毕后的时间；

——集合F(2)中的车流i在决策日内的初始到达时段，即随之前决策日出发的列车运输，并在当前实施日到达的时间.

(3)变量.

p(t(i))——表示决策日结束时，车流i的延误惩罚费用；

——0-1 决策变量，车流i是否选择流经弧a，是为1，否则为0；

ya——非负整数决策变量，弧a对应开行列车的数量.

2.3 目标函数

开行方案构建的目的是为货主提供快捷、准时的运输产品，同时确保铁路运营效益.因此，本文目标函数为车流走行费用，列车开行运营费用和车流延误惩罚费用之和最小.

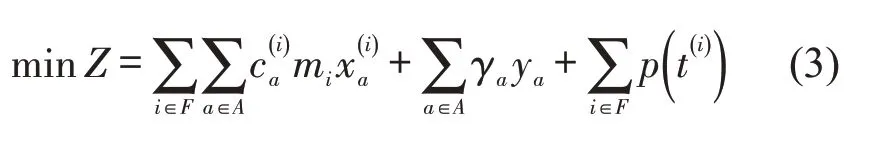
式(3)中，第1 和第2 部分是开行方案编制中运营成本的衡量，第3 部分是对货主需求满足的考虑.

2.4 约束条件

(1)车流径路唯一约束.

车流i只能选择在其始发站至终到站的车流径路上的弧.

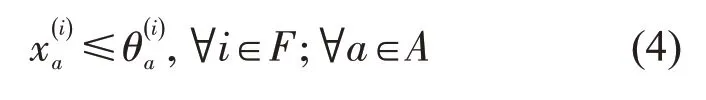
(2)节点流量平衡约束.

为保证车流能够完整地到达目的站，设置节点流量平衡约束为

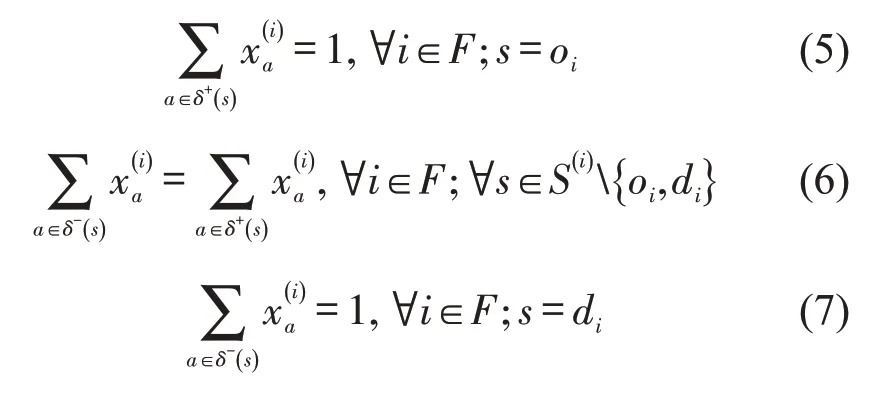
(3)列车编组数量约束.

对于每条服务弧a上计划开行的列车，其编成货车数量不能超过规定的最大编组辆数，也不能低于最小编组辆数.

(4)列车开行数量约束.

对于每条服务弧a，开行的列车数量不能超过该弧相应的最大开行列车数量.

(5)车流中转时间约束.

对于在途中技术站发生中转改编的车流而言，其中转时间应不小于该站的最小有调中转作业时间.同时为防止车流在站停留时间过长，车流在技术站的中转时间应不超过该站的最大有调中转作业时间.

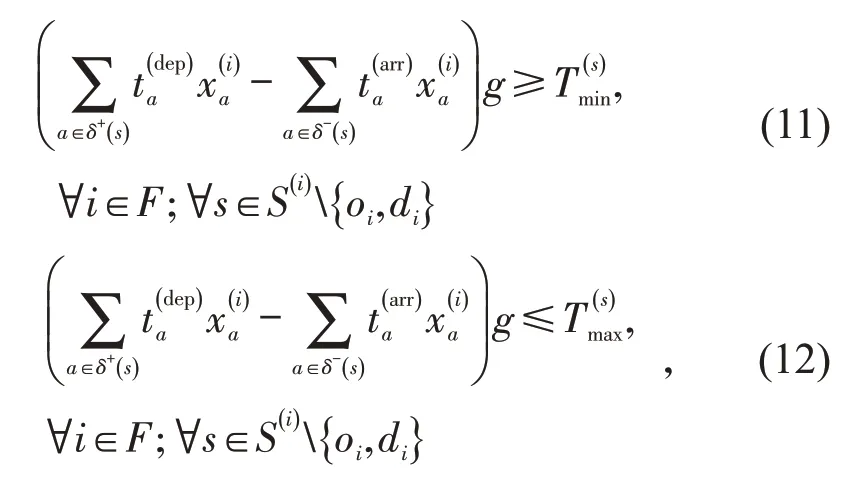
(6)车流始发时间约束.

对于决策日内新产生的车流i∈F(1)，其装车完毕后至出发时间不能超过规定的在站最大和最小停留时间.

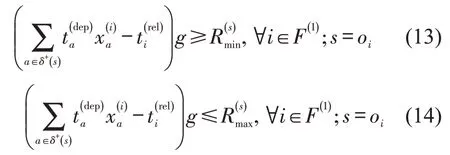
对于之前实施日产生的在途车流i∈F(2)，其在当前决策期内初始站的始发时间也应满足最大和最小在站停留时间限制，该组约束本质也是车流的改编中转时间限制.

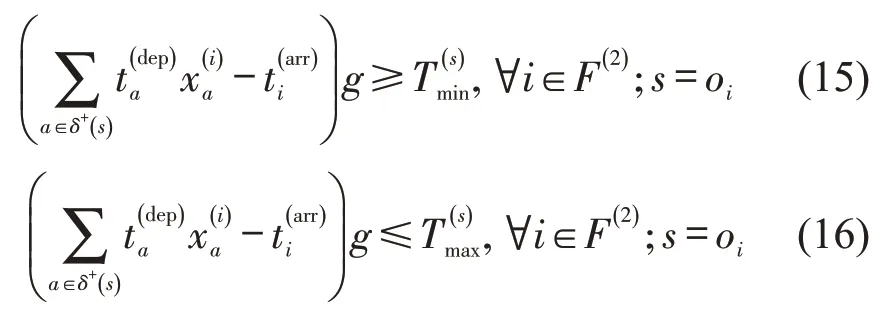
3 算法设计

本文问题本质上是一个大规模组合优化问题，故利用模拟退火(Simulated Annealing,SA)启发式算法，实现问题近似优化求解.传统SA 算法是一种串行算法，为提高算法搜索效率，本文借鉴遗传、粒子群等群搜索算法的隐含并行性特性，通过增加解的个体数目实现算法的并行性；同时，引入多邻域移动准则，通过随机概率决定邻域算子的选择产生邻域解.本文改进的多邻域并行模拟退火搜索算法的总体思路为，建立多个体进行并行搜索，对每个个体利用基于车流排序的分解启发式方法得到模型的解，采用多邻域移动准则随机选择邻域算子探索解空间，利用模拟退火算法控制搜索迭代方向及进程，如图2所示.

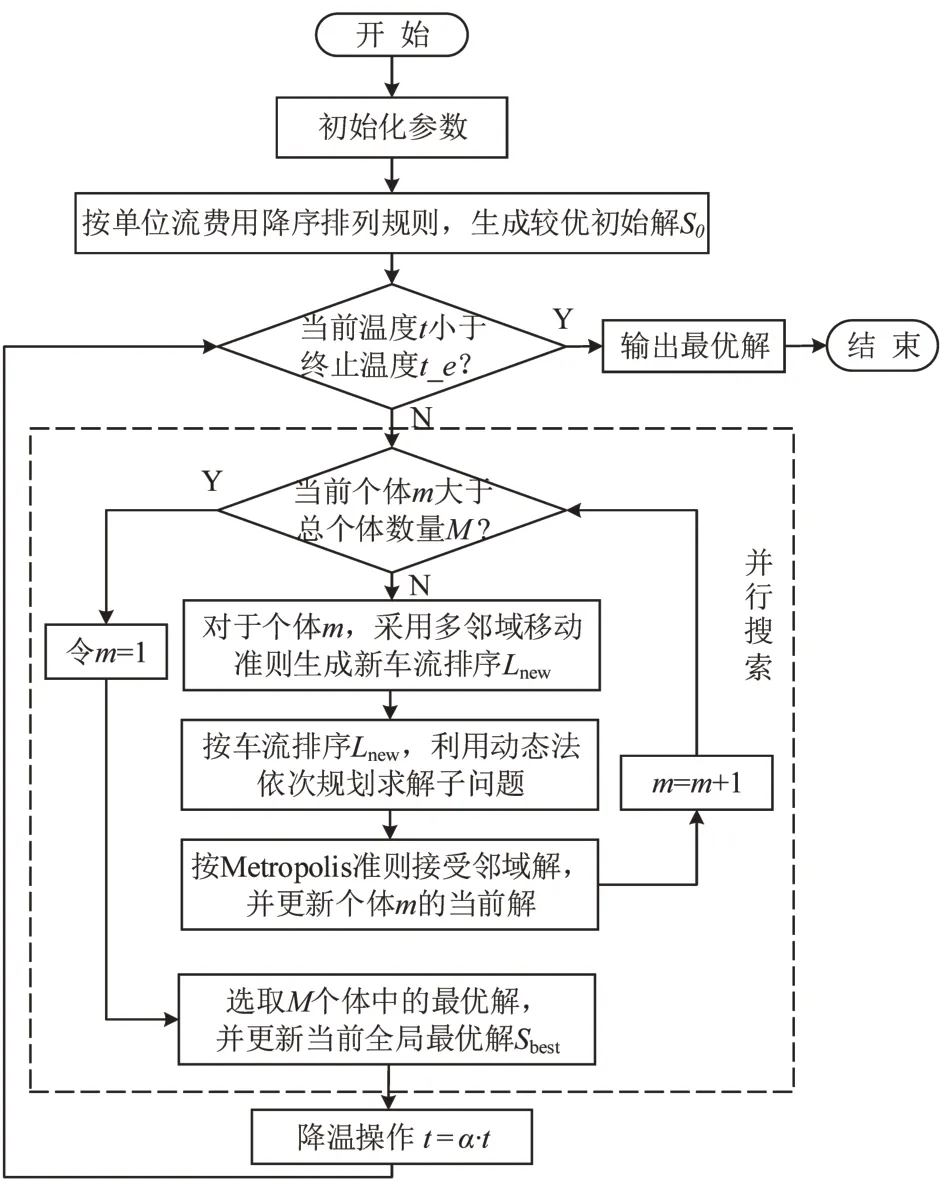
图2 改进的并行模拟退火算法流程图Fig.2 Flow chart of improved parallel simulated annealing algorithm

3.1 求解空间定义

本文模型实际上是一类带容量限制的多商品流模型，弧能力约束式(8)和式(9)，即为“捆”约束，将不同车流联系在一起，而式(4)～式(7)、式(10)～式(16)均作用在单支车流上.优化模型可分解为 |F|个子问题，每个子问题对应单支车流，为该支车流的最短径路问题，可采用动态规划法进行高效求解.与此同时，不同车流所对应的单位流量费用不同，模型为总费用流最小的优化目标，弧能力应优先分配给单位流量费用较高的车流，使得到的解较优.因此，本文提出基于车流排序的分解启发式方法生成模型的解，使算法避免一直陷于不可行解空间寻优.

基于车流排序的分解启发式方法的思路为，松弛约束式(8)和式(9)，并在目标函数中添加相应惩罚项βU，其中，U为列车编组最小辆数不满足的违反量，β为惩罚因子；为提升得到的解的可行性，添加能力约束，即

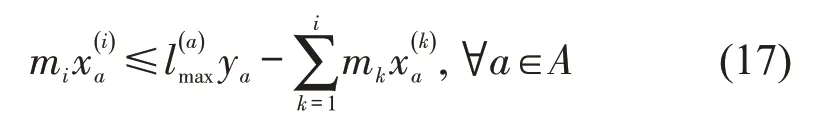
式中：i——当前求解的车流序号；

k——已求解的车流序号.

按照一定的单位流量费用排序，对每个子问题采用动态规划法进行快速求解.每次求解一个子问题后，更新式(17)为该弧加载已求解的车流的剩余能力.最后，由 |F|个子问题的解构成原问题的解.

3.2 分解子问题求解

采用动态规划对单支车流的时空网络最短路径进行高效求解，步骤如下.

Step 1读入目标车流的可选列车服务弧，确定相应的服务网络节点sj(sj∈N)，代表站s(s∈[1,S])第j个节点，以及逻辑起点0，逻辑终点S+1.设立边界条件s=0，f(01)=0，并记录最优值b(01)=0.

Step 2对于s站，遍历s站的服务节点sj，并计算每一个与服务节点sj相邻的服务节点s′j′对应的状态转移函数其中，为车流j在s站中转时间的违反量，u(i)为惩罚系数.若s′=s+1，记录rsj[(s+1)j′]=f(s′j′)；否则，记录tsj(s′j′)=f(s′j′).

Step 3遍历s+1 站的服务节点(s+1)j′，选取，并 记录 为 该节 点的最优值b[(s+1)j′].

Step 4判定s是否等于S+1.否，转Step 2；是，算法结束.

3.3 邻域移动准则

多邻域移动准则设计如下.

(1)插入.随机选取当前车流排序L的一段子序列l1，将其插入到另一个位置，如图3(a)所示.

(2)逆序.随机选取当前车流排序L的一段子序列l1，将其排序逆转，如图3(b)所示.

(3)交换.随机选取当前车流排序L的两段子序列l1、l2，交换l1和l2的位置，如图3(c)所示.

图3 邻域算子Fig.3 Neighborhood operators

4 案例分析

以蒙华铁路为例进行案例验算，如图4 所示.某决策日内共23 座车站涉及列车的始发终到，依次编号S1～S23，该决策日共有125支车流，当日蒙华基本列车运行图共包含182条运行线.以阶段计划的3 h进行决策日时段划分，车流时间窗由式(1)计算得到，相关参数取值为：vtravel=34.3 km/h，ttransit=4.8 h，Ltransit=208 km，Lunload=10 h.车流最小、最大中转时间分别为3 h，6 h，车流单位流费用及列车单位开行费用参考文献[1]和[2]设置，车流单位延误费用设置为5元/min.

在处理器为i7-6700HQ，内存为16 G的个人计算机上，采用Matlab 2016a 实现编程求解.经过多组参数实验，在初始温度为200，终止温度为1，温度衰减系数为0.85 的设置下，求得蒙华铁路货物列车开行方案，如图5和图6所示，其中，列车编组内容以车流序号和车辆数表示.

总目标函数值为86 233元，其中，车流总费用为41 868元，列车总开行费用为44 365元，总延误费用为0元，即车流都能在规定时间窗内到达目的站.下、上行方向各开行列车26 列，列车编组长度满足编组数量要求，从而说明本文模型和算法的有效性.

为进一步分析运到时限对开行方案的影响，在本文算例的基础上，对不同运到时限方案(12，24，36，48 h)进行计算，结果如图7 所示.由图7 可知：当运到时限不断缩减时，车流走行费用、列车开行费用增加，延误费用保持不变，说明通过增开列车，加快车流输送，可保障运到时限；当运到时限进一步缩减时，车流费用、列车费用降低，而延误费用增加，说明当无法进一步加快车流输送时，通过少开列车来降低运营成本.

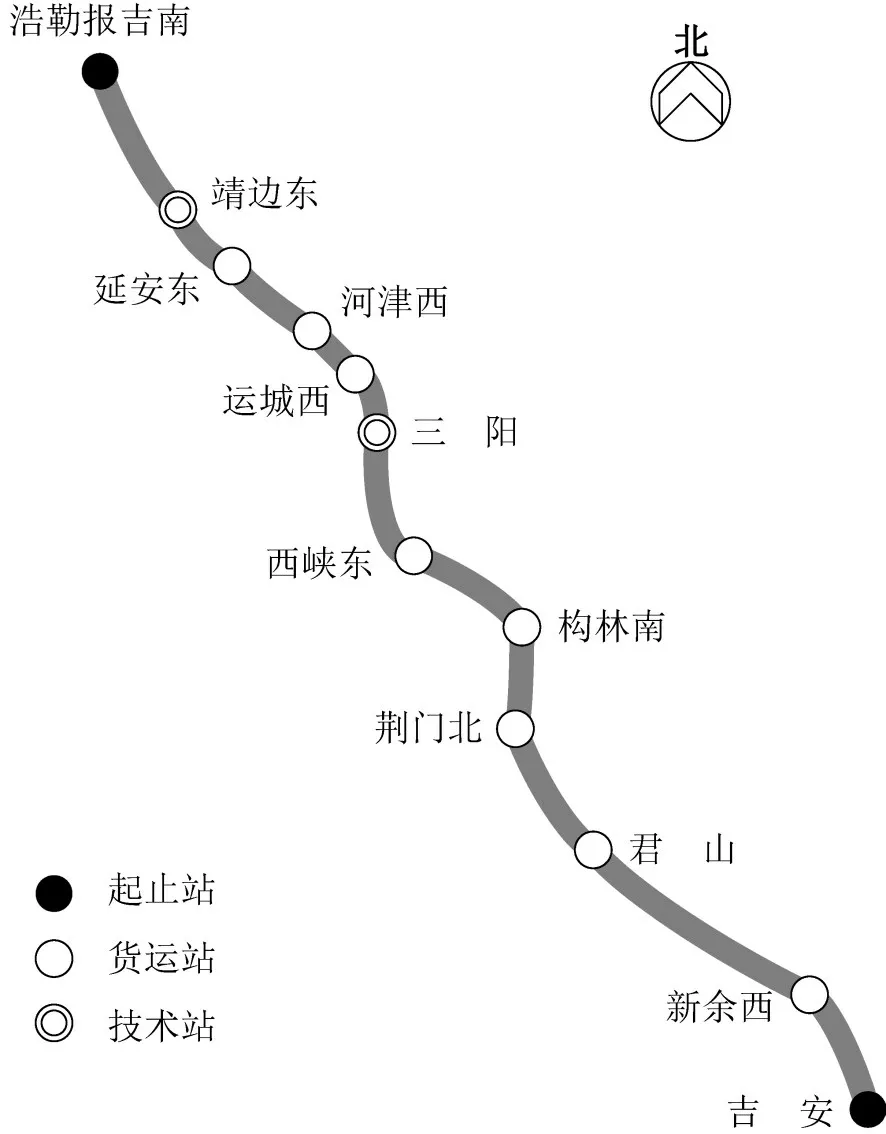
图4 蒙华铁路示意图Fig.4 Sketch map of Menghua railway

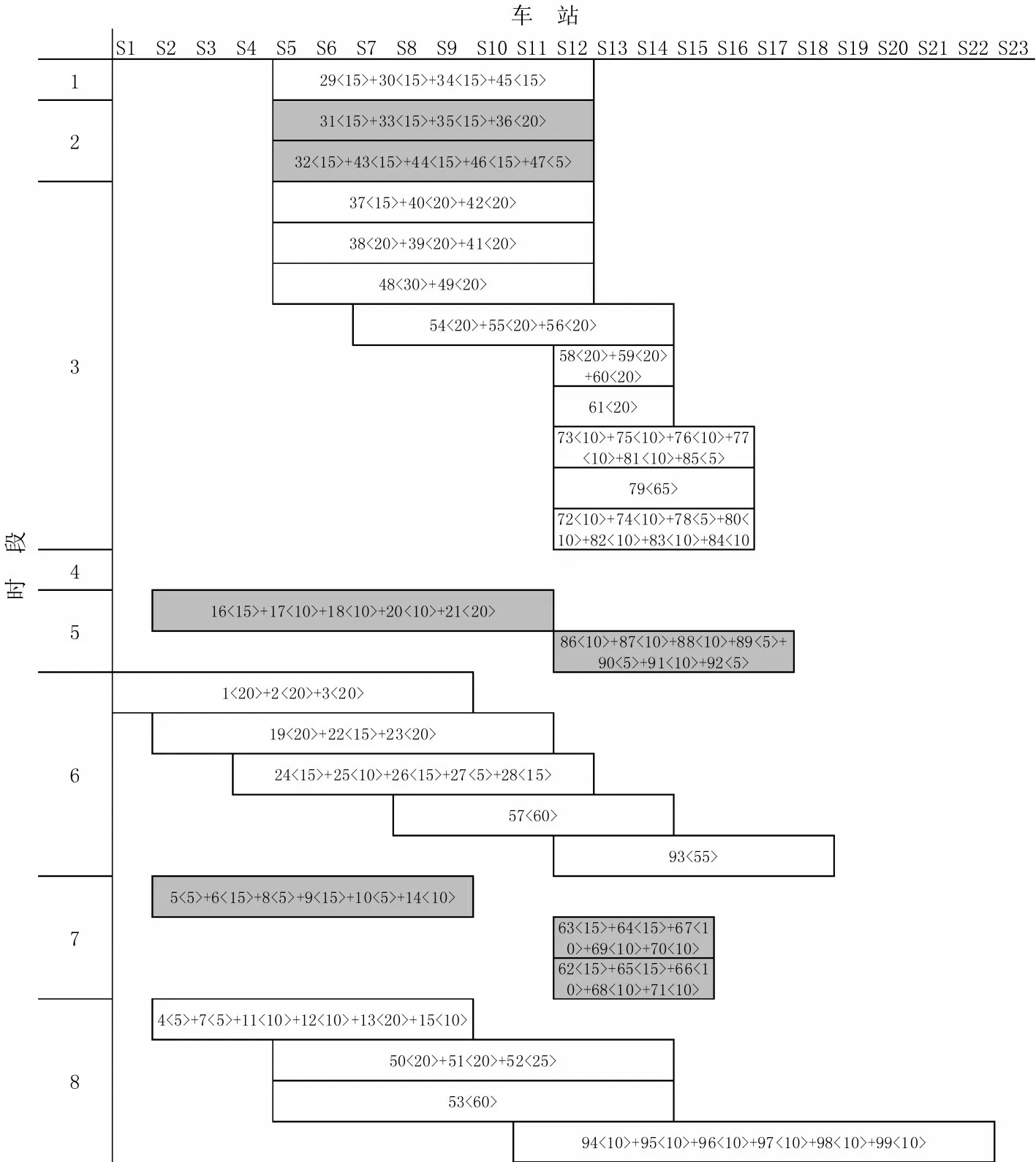
图5 蒙华铁路开行方案(下行方向)Fig.5 Tran formation plan of Menghua railway(Haolebaoji South-Ji'an)

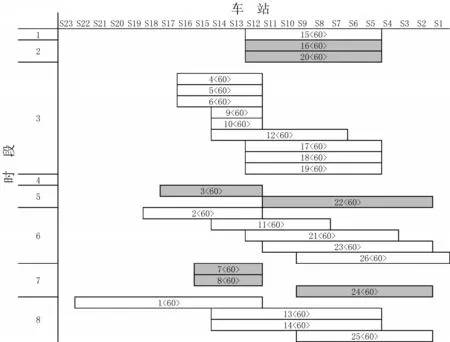
图6 蒙华铁路开行方案(上行方向)Fig.6 Tran formation plan of Menghua railway(Ji'an-Haolebaoji South)

5 结 论

本文提出日常货物列车开行方案的编制优化方法，其相较于中长期层面的开行方案，在对动态车流异质性区分的基础上，确定了列车开行的始发终到站、开行数量、编组内容和开行时段.构建开行方案编制的整数规划模型，并设计改进的多邻域并行模拟退火算法求解；并通过蒙华铁路的实际算例，说明本文的模型及算法的有效性.未来可研究分组列车开行方案的编制问题.