城市公交线网差异化计程票价多目标优化

李雪岩，祝 歆，李 静

(1.北京联合大学管理学院，北京100101；2.北京交通大学经济管理学院，北京100044)

0 引 言

城市公共交通系统多模式网络化进程不断加速，差异化票价改革方案不断被提出，但目前公共交通系统既有价格机制与差异化策略仍缺乏灵活性，造成运力配置缺乏科学性等问题[1].

城市公共交通系统票价的差异化研究多针对运输方式之间的竞争策略、时段差异[2]、优惠措施[3]、排放补贴[4]或一票制[1].差异化票价的理论基础来源于网络拥挤收费思想[2]，既有研究表明，相对于一票制，分段票制更加具有优势[5]，故引入差异化计程票制更加符合公共交通服务多元化发展的实际需求.公共交通具有公共资源属性，社会成员具有有限理性与利己性，并不能总是保持理性合作，容易造成资源使用的社会困境.当个体偏好与获得效用受到决策环境影响，会对宏观政策产生阻碍或放大作用，使整体均衡发生转移，这一现象已被社会学领域相关研究所验证[6].此外，公交系统票价优化要考虑多个决策目标，如票价收入、出行成本，现实中很难精准测定不同目标的先验权重，故票价结构应该是一组供决策者进行多角度权衡的帕累托最优解.

本文基于差异化计程票制，引入后悔理论与社会交互机制刻画出行行为，建立更加符合实际需求特征的多目标公交票价优化模型，采用集群智能优化算法求解，通过优化票价方案提升运营收入，降低出行成本，有效诱导交通流.

1 问题描述

定义路网G=(V,E)，V为起讫站点集合，E为路段集合；R为公交线路集合，每条线路由站点和路段组成；D表示路网G的OD 固定需求矩阵，其中，di,j为站点i,j间需求，i,j∈V，N为站点数量.在起讫点i,j之间，出行者在不同公交线路(无换乘)与私家车之间选择，i,j间公交线路r上承担的客流为1,2,…,R)，由于公交与私家车之间、不同公交线路间存在竞争，客流会在私家车及不同公交线路间转移.不同公交线路具有不同的单位里程基准票价Pr，乘客依据行程长短支付费用；若选择私家车，则需要支付停车费.公交单位里程基准票价、发车频率及停车费为优化变量.

2 乘客出行选择行为

2.1 广义出行费用

(1)候车时间成本.

对于公交出行，乘客以泊松过程到达车站，强度为λ，出行者x到达车站的时刻为tx，线路r发车频率为fr，fmin≤fr≤fmax，fmin，fmax分别为最小、最大发车频率.乘客的到达视为相互独立的随机变量，服从上的均匀分布，即，总体等待时间期望值为表示t时刻到达的乘客数量，候车时乘客的心理感受符合对效用的感知过程[7]，故将物理时间转换为心理时间则候车心理时间期望Ep为

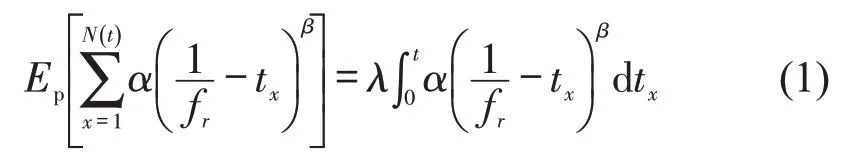
式中：α，β分别表示出行目的影响系数、注意力系数[7].

求解式(1)可得，乘客平均候车心理时间τr=对于私家车，候车心理时间为0.

(2)行程时间成本.

OD 对i,j间选择线路r的行程时间用表示；私家车的行程时间为即该OD对间的最短公交行程时间.

(3)舒适度成本.

假设公交线路r由N个站点构成，令与分别表示公交线路r上行方向(“+”)与下行方向(“-”)站点i到i+1之间的流量，则有

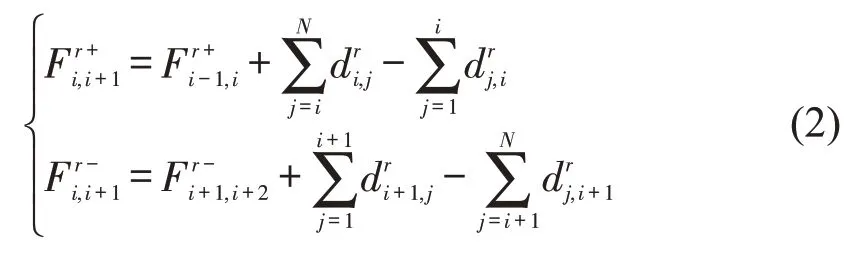
线路r在站点i与j间舒适度成本为

式中：Ψr表示线路r上公交车的定员；η为舒适度系数；s为站点序号，s=i,…,j-1.私家车不产生舒适度成本.

(4)经济成本.

对于公交车，经济成本为票价，令公交线路r的单位里程票价为Pr，Pr,min≤Pr≤Pr,max，Pr,max，Pr,min分别为公交票价的上、下限，站点i与j间在公交线路r上的距离为为公交时速，则乘客需支付对于私家车，经济成本为路网内的停车费Pp，Pp,min≤Pp≤Pp,max，Pp,max、Pp,min分别为停车费的上、下限.

(5)社会互动乘数效应.

出行者之间存在社会互动作用，表示为I，令εx=1表示选择公交，εx=-1表示选择私家车，μx，μy分别为出行者x，y对路网内选择其他出行方式人数的主观期望，为站点间平均需求，依据乘数互动作用原理[6]有

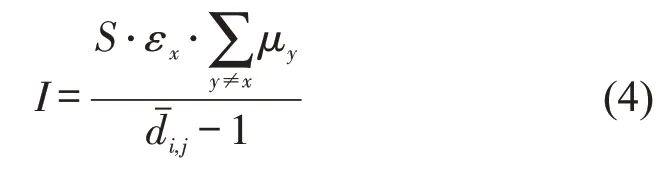
式中：S表示社会互动强度.

综上，OD 对i,j间出行方式m的广义出行费用为

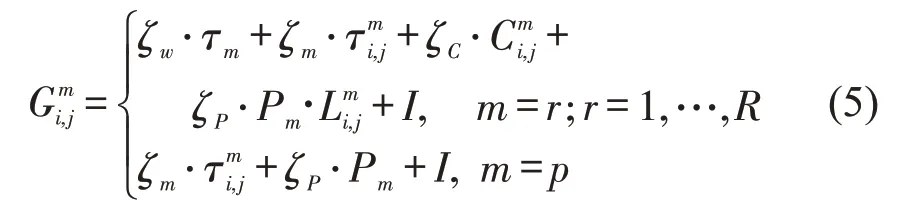
式中：ζw，ζm，ζC，ζP为单位成本转化系数；分别为候车时间、行程时间、舒适度成本、经济成本.

2.2 出行选择模型

后悔理论模型构造经历了由经典的RRM1 到RRM2再到兼顾阻抗与“后悔感觉”的改进[8]过程，本文结合第3种模型构造思想与上述出行场景，建立模型.

后悔成本为

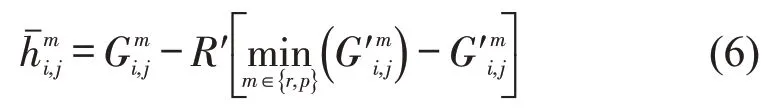
式中：为式(5)中去除社会互动作用的广义出行费用；R′(x)表示为

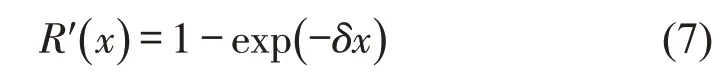
式中：δ为后悔厌恶水平，δ越大，出行者越厌恶后悔.令θ表示出行者对效用的感知准确度，OD对i,j间选择出行方式m的客流表示为

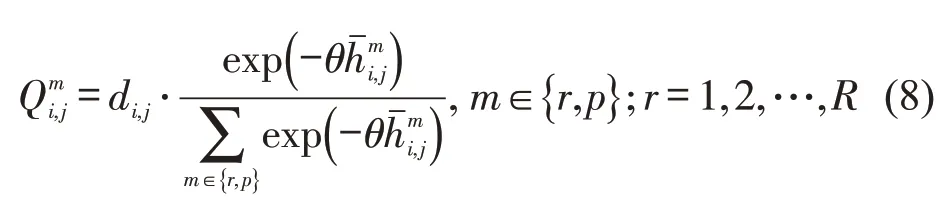
3 群体出行偏好均衡描述

3.1 线路客流OD矩阵均衡算法

在给定由不同线路票价Pr、停车费Pp及发车频率fr构成的决策向量(P1,…,PR,Pp,f1,…,fR)基础上，考虑出行者舒适度成本与社会互动乘数效应的不断更新，可通过迭代算法得到与(P1,…,PR,Pp,f1,…,fR)对应的OD客流矩阵，设计迭代算法如下.

Step 1对任意(P1,…,PR,Pp,f1,…,fR)，令初始舒适度成本与社会互动乘数效应I0为0，迭代次数k=0，利用式(8)计算各出行方式的客流OD矩阵

Step 2将带入式(2)，计算各条线路的路段流量与，通过式(3)得到不同出行方式的舒适度成本；由可得出，选择不同出行方式的人数和，带入式(4)，得到Ik+1.

Step 3依据式(5)计算广义出行费用矩阵.

Step 4利用式(8)更新客流OD 矩阵，得到

Step 5对于所有m∈{r,p} ,r=1,…,R，设定为停止条件.若收敛，则为当前(P1,…,PR,Pp,f1,…,fR)所对应的客流OD矩阵；否则，令k=k+1，转Step 2.

3.2 基于社会交互的群体出行偏好均衡分析

在公交车与私家车选择中，出行者会对其他人的行为产生预期，这种主观判断可用期望值μx=E(εy)表示，由文献[6]的分析可知，基于Logit模型的自我一致均衡可以表示为

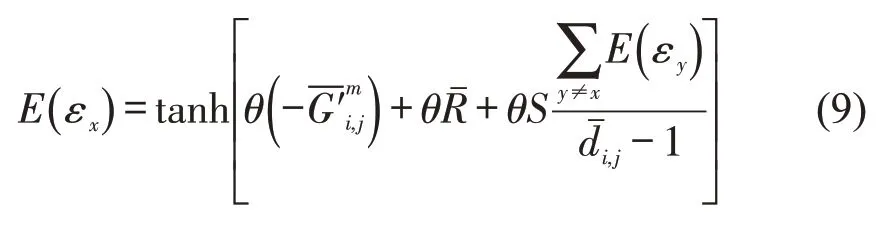
全体出行者的社会均衡表示为

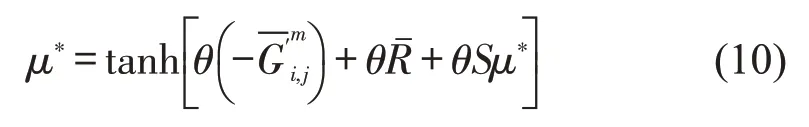
式中：μ*为出行者行为处于均衡状态时，路网对公交或私家车的平均选择水平.可见，价格与有限理性因素均会使均衡发生转移.

4 多目标票价优化模型建立

4.1 目标函数与约束条件

交通管理部门一方面要使交通系统产生的利润最大化，另一方面要使出行者的出行效用最大化，即广义费用的相反数.现实中很难精准确定两目标的先验权重，故引入帕累托最优思想，即

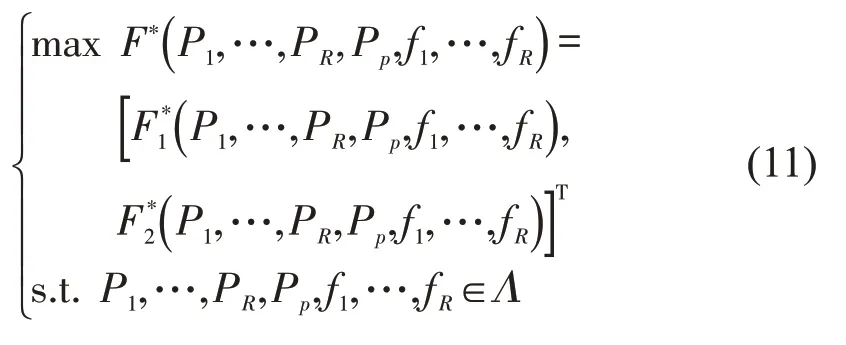
式中：Λ表示解空间.

交通管理部门的目标函数为

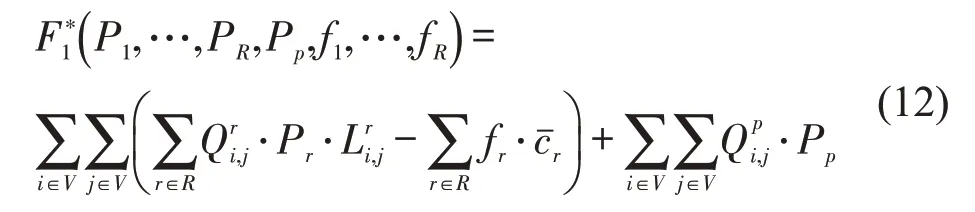
式中：为平均运营成本；由通过线路客流OD 矩阵均衡算法得到.

出行者效用的目标函数为

约束条件为 ：Pr,min≤Pr≤Pr,max，Pp,min≤Pp≤Pp,max，fmin≤fr≤fmax.

4.2 模型求解算法

基于复杂网络拓扑结构的集群智能多目标优化算法求解本文模型，流程如下.

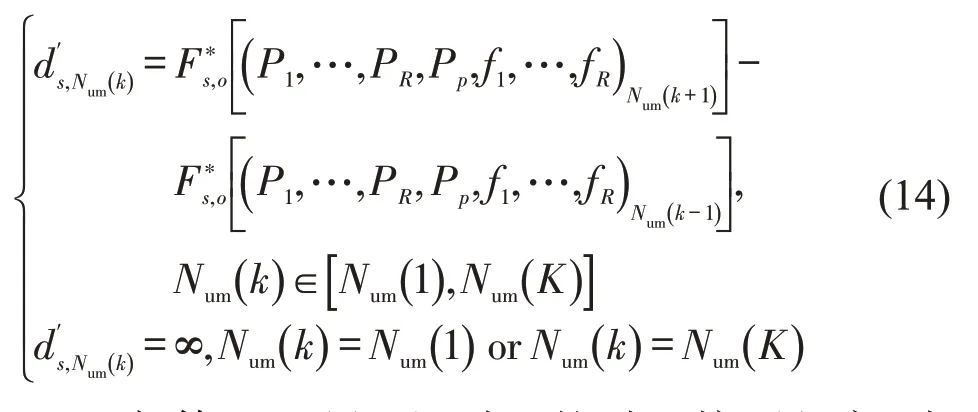
则第Num(k)组解的拥挤距离为.

Step 6选择.对于个体(i′,j′,k′)，首先，按照Step 5 的方法计算Bi′,j′,k′中每组解的拥挤距离；其次，依据轮盘赌法，在Bg与Bi′,j′,k′内各选择一个优秀个体.以Bg为例，Bg中拥挤距离之和表示为则第Num(k)组解被选中的概率为记Bi′,j′,k′中选出的个体为(i″,j″,k″)，Bg中选出的个体为(i‴,j‴,k‴).

Step 7交叉.令X=(P1,…,PR,Pp,f1,…,fR)，利用正态分布算子生成局部最优(i″,j″,k″)与全局最优(i‴,j‴,k‴)交叉后的新个体Xi′,j′,k′为

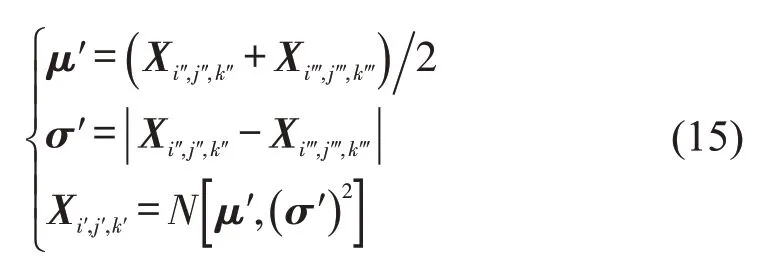
Step 8变异.设置变异概率pm，每个个体依概率pm发生变异，对于个体(i′,j′,k′)所代表的解(P1,…,PR,Pp,f1,…,fR)i′,j′,k′，利用cat 映射生成混沌序列为

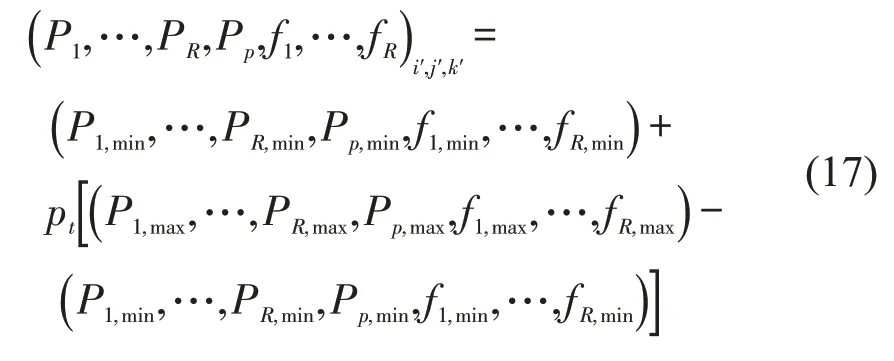
Step 9判断算法是否满足终止条件(全局非支配解集不再发生变化).若满足，算法停止；否则，返回Step 3.

模型优化算法流程如图1所示.

图1 算法流程Fig.1 Algorithm flow

5 票价优化结果

5.1 算例路网结构及参数

以Mandl 基准路网(1980)为例，对本文提出的模型与算法进行验证，如图2 所示，每条边上的数字表示站点间运行时间(min).

Mandl 基准路网站点间的OD 需求详见文献[1]，为保证路网中每个OD 对间都有公交线路连通，设计公交线路如表1 所示.若后文无特别说明，模型参数按照表2取值.其中，参数S的取值数量级依据文献[6]的回归结果得到，参数的取值数量级依据文献[1]得到，参数Pr,max，Pr,min，Pp,max，Pp,min依据目前市场价格平均水平取值.

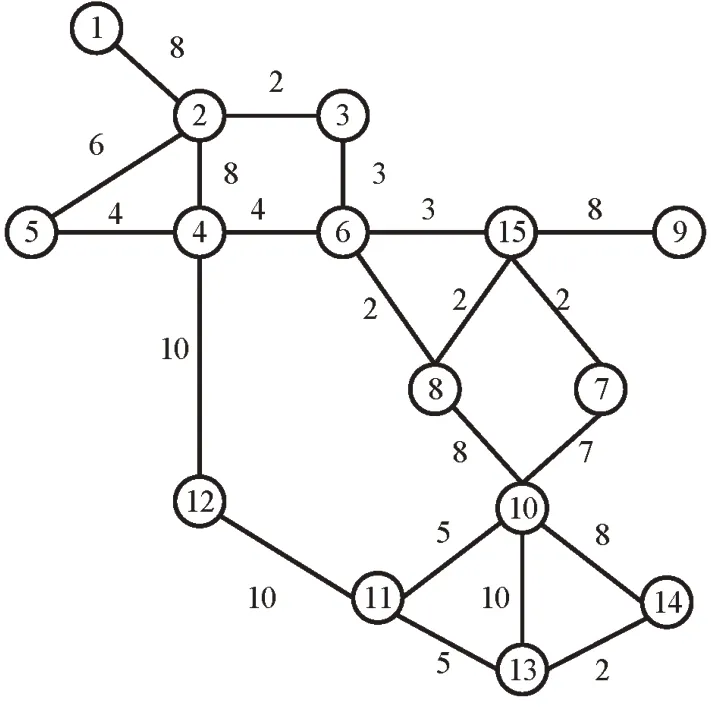
图2 Mandl 路网Fig.2 Mandl network

表1 公交线路设计Table 1 Bus line design

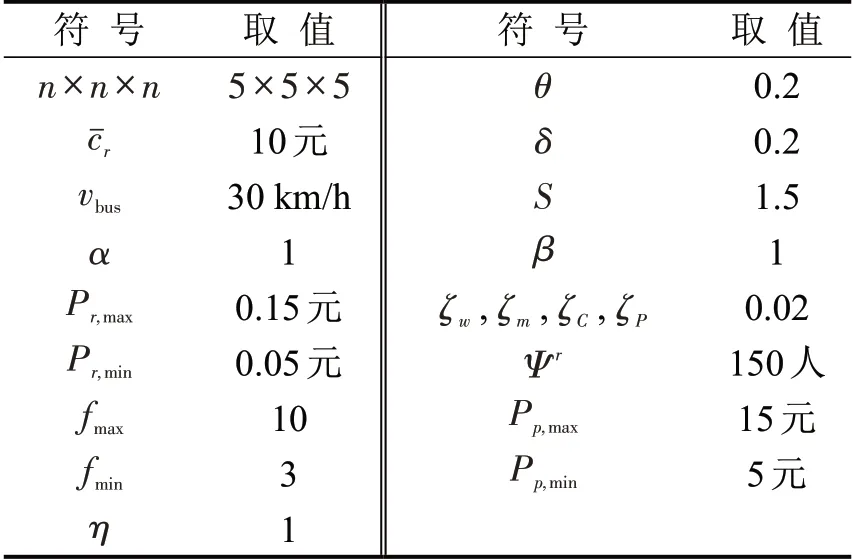
表2 模型参数Table 2 Parameters of model

5.2 OD矩阵均衡算法收敛性

首先通过数值模拟验证OD 矩阵均衡算法收敛性.如图3 所示，纵轴为的取值.可见，迭代7次后，OD间客流量收敛，说明本文提出的OD矩阵均衡算法具有收敛性.

5.3 模型优化结果

将表2 参数带入本文算法对公交票价进行优化，同时与一票制的优化结果进行对比.一票制票价为表2 中的单位里程票价区间中值(0.1 元)与5条线路的平均里程的乘积.两种计价模式得出的帕累托前沿(一票制方案中仅对公交发车频率与停车费进行优化)如图4所示.

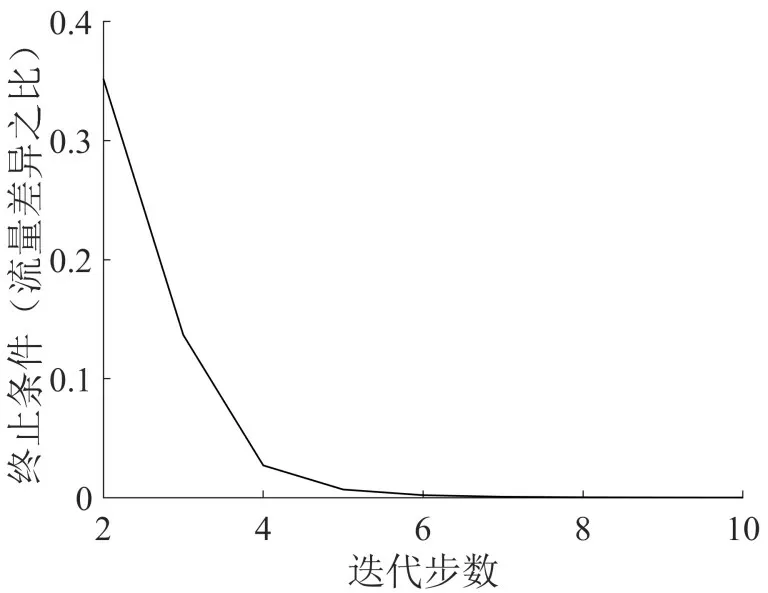
图3 OD 矩阵均衡算法收敛性Fig.3 Convergence of OD matrix equalization algorithm

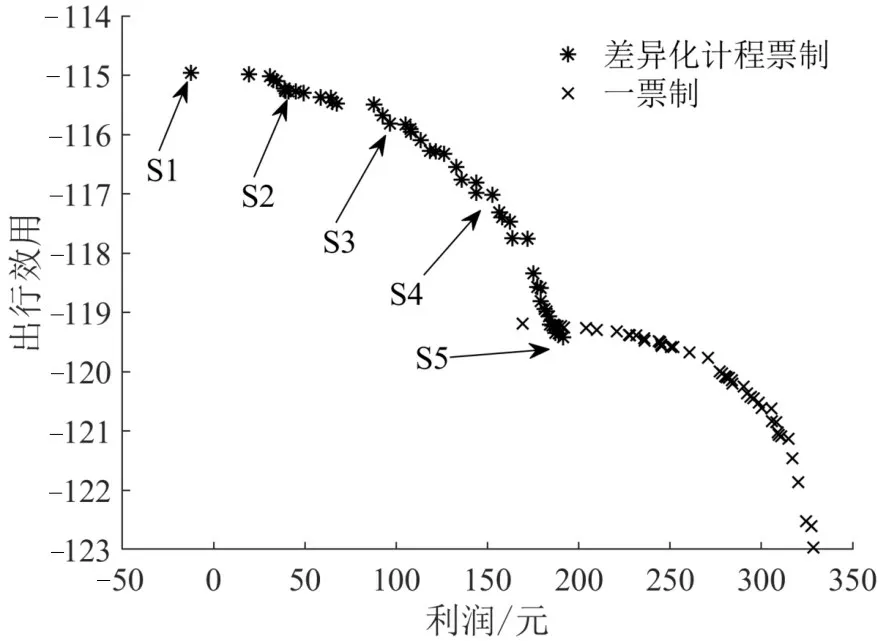
图4 票价优化结果Fig.4 Fare optimization results

由图4 可知，相比于差异化计程票制，一票制使交通管理部门获取了更高收入，但也提高了出行成本.对差异化计程票制形成的帕累托前沿进行四等分，选取代表性票价方案1～方案5(S1～S5)，给出各方案优化结果，如表3和表4所示.表5为不同票制下全路网所有OD 间平均候车时间对比结果，相比于总发车频率最高的一票制方案，差异化计程票方案S1可进一步减少候车时间.

5.4 有限理性对帕累托最优解的影响

图5 为有限理性对帕累托最优解的影响.由图5(a)可知，社会交互强度S增大时，出行者效用增加，交通管理部门总利润减小；由式(4)和式(5)及OD 矩阵均衡算法的Step 2 可知，社会交互为出行者提供了对不同出行方式效用的预判，而当交互强度增加到一定程度时(大于2.5)，帕累托前沿趋于稳定，说明此时出行者对效用的感知精度已经无法通过社会交互获得改进.由图5(b)可知，出行者后悔厌恶水平的提升使其整体出行效用升高，出行者越厌恶后悔，对出行效用的判断越接近客观可观测的出行效用.可见，出行者准确掌握效用信息有助于降低出行成本.

5.5均衡转移票价政策影响机制分析

当出行者的社会交互行为满足式(9)时，社会均衡满足

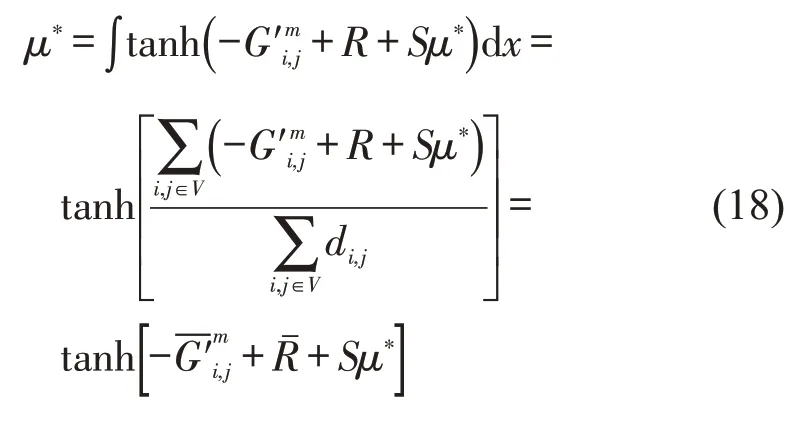
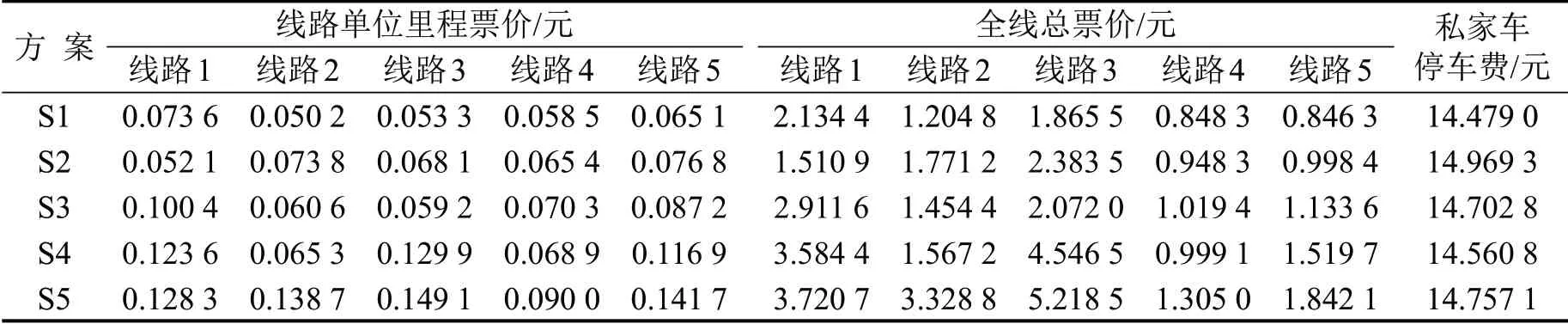
表3 票价优化结果Table 3 Fare optimization results

表4 发车频率优化结果Table 4 Optimization results of departure frequency

表5 全路网平均候车时间Table 5 Average waiting time of whole network

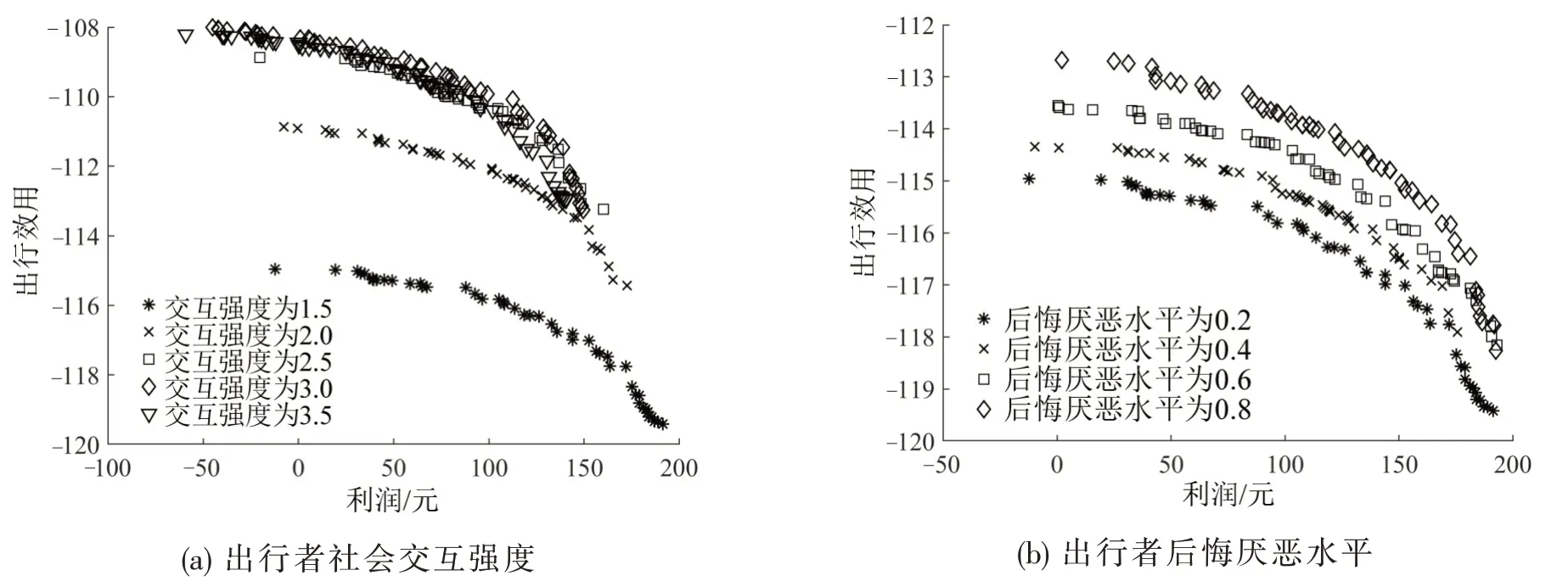
图5 有限理性对帕累托最优解的影响Fig.5 Influence of bounded rationality on Pareto optimal solution

基于本文模型优化结果，对路网均衡状态下 的出行方式选择比例进行数值分析，考察不同票价方案对出行选择均衡的影响.

图6(a)为社会交互强度S=1.5 对应的方案1与方案5的模拟结果，此时基于帕累托最优解的票价方案并不能使出行者达到均衡，但相对于方案5，具有效用提升特点的方案1 使主观期望曲线向有着利于均衡的方向移动.令S=3 得到图6(b)，将社会交互强度提升至一定程度后会产生均衡，与图5(a)的结果一致，即社会交互强度的增加使帕累托前沿趋于稳定.定义选择公交人数比例大于0.5的均衡点为优势均衡，由图6(b)可知，当票价降低时，出行者群体选择会从非均衡状态转移至“稳定优势均衡”(接近方案5)，再转移至“优势均衡”(方案1)状态.可见，对于交通管理部门，增加准确的出行信息在系统中的传播力度可以促进均衡生成；在帕累托最优解的基础上进一步调节票价，可使均衡向着鼓励公交出行的稳定优势均衡转移.

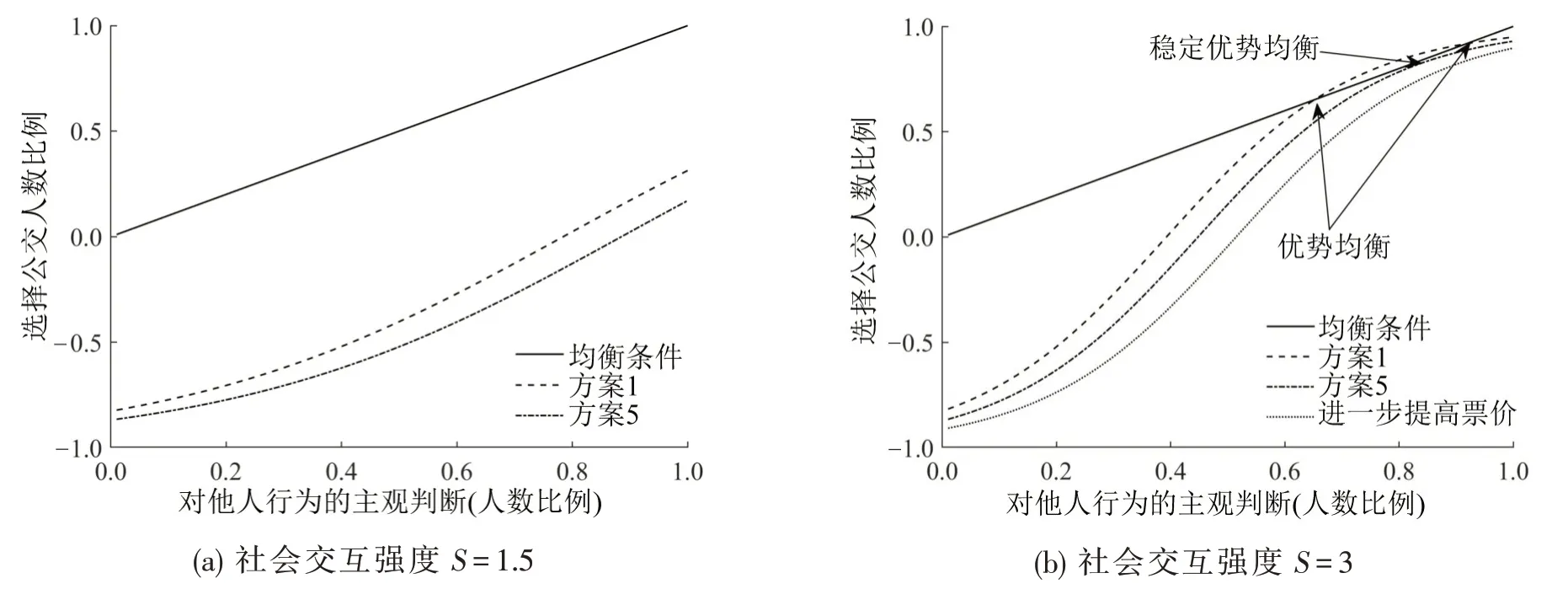
图6 出行者群体选择均衡Fig.6 Group selection equilibrium

6 结 论

本文基于差异化定价思想，设计了考虑出行者行为因素的多目标公交线网计程票价优化模型.基于标准线网的优化结果表明：差异化计程票制有助于降低出行成本，减少候车时间，同时也要配合增加准确出行信息的社会传播力度，帕累托最优票价体系丰富了票价的调节机制且具有可操作性，可为交通管理部门鼓励公交出行提供更加精细化的决策支持.