基于混合深度学习的地铁站进出客流量短时预测

赵建立，石敬诗，孙秋霞，任 玲，刘彩红

(1.山东科技大学a.计算机科学与工程学院，b.数学与系统科学学院，山东青岛266590；2.青岛地铁集团有限公司，山东青岛266000)

0 引 言

随着数字城市的飞速发展，以及IC 卡的大量普及，公共出行的数据挖掘与预测成为新的研究热点.本文分析地铁站的历史刷卡数据，对多站点的进出客流量进行短时预测.不仅可以帮助出行者合理地选择出行路线，规避交通拥堵；也可帮助地铁运管部门提前安排车次调度，部署站点安保措施，具有重要的研究价值.

轨道交通流量预测模型主要分为3类.第1类是基于时间序列的统计模型，白丽[1]利用ARIMA模型分析地铁站每日客流量的历史数据，实现常态的日客流量预测，但其局限于单变量预测与时间分析，没有考虑空间因素.第2 类是基于非参数的预测模型，郇宁等[2]基于改进的K 最近邻算法，实现轨道交通中进站客流的短时预测；Tang等[3]构建时空长短期记忆(ST-LSTM)网络，用于多个站点的出站客流量预测.这两类模型都实现了多站点的同步预测，但没能实现进出客流量的同步预测.

第3类是基于多特征提取的混合模型.Ma等[4]将地铁客流数据先转换为客流图像与时间序列，再运用卷积神经网络(CNN)和双向LSTM 分别提取空间与时间特征；该方法需要对研究区域进行网格划分，大量无用网格会增加计算负担.Liu等[5]利用LSTM 挖掘时间特征，基于嵌入层与全连接层融合空间特征、外部环境及地铁运营等多源信息.Zhang 等[6]结合残差网络、图卷积网络和LSTM构建客流量预测模型，并融合了天气与空气状况.多源信息的加入可提升预测精度，但多源信息的收集与处理难度大，使模型过于复杂.

综上，本文构建一个新的适用于轨道交通的客流量预测模型.该模型简洁、易操作，聚焦于客流量的时空特征挖掘.将每个时间段进出站的客流量数据用特定的张量格式表示，利用卷积神经网络与残差网络分别建模，挖掘时间与空间特征.最后通过加权融合的方式，得到目标时间段中多站点进出客流量的预测结果.

1 问题描述

地铁站的短时客流量预测是一个典型的时空序列预测问题，即利用已有的r个历史观测值预测下一个时间步的客流量Xt，其中，n表示时间步编号.表示第t个时间步m个站点的客流量观测值，其中，2 为进站与出站两种客流，m为站点的总数量，Si(t)为第t个时间步站点i(1 ≤i≤m)的观测值，即

如图1 所示，输入模型的观测张量可以表示为X∈ℝr×2×m，图中，Si表示第i个站点的客流量观测值.

图1 地铁站的进出客流量Fig.1 Subway station passenger inflow and outflow

2 构建模型

地铁作为通勤人员的重要交通工具，其客流量波动具有一定的时间与空间特征.对于单个地铁站，主要考虑时间特征的挖掘，例如工作日，地铁客流会出现早晚高峰，车站的人流量相对较大；对于多站点客流量预测，除时间特征外还需考虑空间特征的影响，例如某一站点的进站客流突然增加，会影响其他站点的出站客流量.为充分挖掘这些时空特征，本文构建混合深度学习模型.首先，将二维卷积神经网络(Two Dimensional Convolutional Neural Network, CNN2D)与残差网络(Residual Network,ResNet)组成深层网络挖掘空间特征，利用一维卷积神经网络(One Dimensional Convolutional Neural Network, CNN1D)挖掘时间特征；然后，基于参数矩阵融合方式，将时空特征加权融合为Xfusion；最后，通过激活函数得到最终预测值模型简称为ResNet-CNN1D模型，结构如图2所示.

2.1 空间特征建模

挖掘空间特征的模型是由二维卷积层(CNN2D，简称CNN)和残差网络(ResNet)组成的深层网络.将客流量的观测张量X∈ℝr×2×m输入第一个二维卷积层，连续堆叠L个残差单元，再加入一个二维卷积层，其中，二维卷积结构如图3所示.

图2 ResNet-CNN1D 模型Fig.2 ResNet-CNN1D model

图3 中，卷积核大小为3×3，单个卷积层只能考虑局部空间的依赖性，适当增加网络深度可以相应增加最后卷积层的感知野，扩大空间依赖范围[7].地铁站的空间关系中，并不局限于邻近站点，以青岛市地铁3号线刷卡数据为例，统计1周内乘客出行的OD(Origin-Destination)信息，如图4 所示.可知，乘客地铁出行的OD 站点间隔为6 站的最多，休息日与工作日的短距离出行(1 站以内)分别占总出行量的6.2%和5.3%.因此，有必要设计一个多层卷积网络，捕捉间隔遥远站点间的空间依赖关系.青岛市地铁3号线的站点数量为22个，若要挖掘所有站点之间的依赖关系，至少需要10 个连续的卷积层堆叠.

网络深度对模型的空间特征挖掘有很大帮助，但深度过度增加，模型精度会停滞甚至下降.针对这种“退化”现象，He等[8]提出使用残差网络帮助模型训练.图5是ResNet-CNN1D模型中构建的残差单元，其公式为

(2) 随着排水管壁面积的增大，整个系统的渗流量也随之增大，土体细颗粒流失速度加剧，土体内部渗流通道的发育速度也加快。在试验过程中，不同土体梯度比Gr值在下降一段时间后开始缓慢上升(如图3所示)，分析可知：在水的渗流力和压重的双重作用下，土体内细颗粒被带动向排水管壁表面及孔隙中移动，土体内的渗流通道开始发育，细颗粒在流经排水管壁时会滞留在排水管壁表面或者淤积在排水管壁孔隙中，当渗流通道发育完全后，梯度比GR值不再下降而是随着滞留在排水管壁表面或淤积在排水管壁孔隙中的细颗粒含量的增大而缓慢上升。

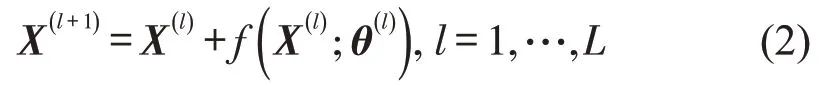
图3 二维卷积Fig.3 Two-dimensional convolution

图4 OD 距离统计Fig.4 OD distance statistics

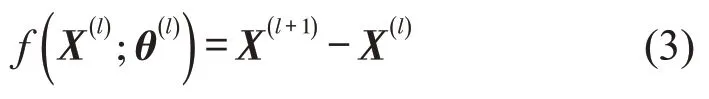
式中：X(l+1)为残差单元的潜在映射；X(l)为残差单元的输入；f(·)为残差函数，即神经网络中实际训练的映射，本文利用2个激活层(ReLU)和2个二维卷积层构建残差函数；θ(l)为在第l层中所有的可学习参数.ResNet-CNN1D 模型中L=4，这样就构建成10 个卷积层堆叠的深层残差网络，用于捕捉站点间的空间特征Xspatial.

2.2 时间特征建模

利用一维卷积网络(CNN1D)捕捉客流量的时间特征.CNN1D 使卷积核在时间轴上执行特征检测，对每个输入序列执行相同的输入变换，故在时间轴上某个位置学到的特征稍后可以在其他位置被识别.相比于广泛应用的循环神经网络(RNN)，CNN1D 不仅可以更好地并行训练，减少模型训练时间；还不受先前时间步的数据限制，可以更好地捕获数据的急剧变化[9]，比如早晚高峰期间客流量的剧烈波动.

图5 残差单元Fig.5 Residual unit

图6 为CNN1D 结构示意图，先将输入序列重塑为X∈ℝ(r×2)×m，其中，r为输入序列的时间步数量，r×2 为输入序列的长度.卷积核u∈ℝk×m，k为卷积核的长度.序列X与卷积核u进行卷积，可以生成一个特征映射E∈ℝ(r×2-k+1)×1，即

式中：*表示卷积；b为偏置项；g(·)为激活函数.

图6 CNN1D 结构示意图Fig.6 Schematic diagram of CNN1D structure

利用维度相同的n个卷积核，生成n个特征映射，重新排列组成序列X的特征图V∈ℝ(r×2-k+1)×n，即

式中：“；”为列向量的连接；En为由第n个卷积核生成的特征映射.

2.3 特征融合

ResNet-CNN1D模型采用参数矩阵融合方法，将空间特征Xspatial与时间特征Xtemporal进行加权融合，公式为

式中：×为Hadamard 乘积；为目标时间t的预测值；Wspatial，Wtemporal为可学习的参数矩阵，分别调整融合结果受空间特征与时间特征的影响程度；融合结果通过激活函数g(·)得到最终预测值.

3 模型估计及实证分析

3.1 数据集划分与评估标准

数据来源2017年8月1日～10月31日青岛市地铁3号线进出站刷卡数据.青岛市区当时只有这一条地铁线路，不存在地铁换乘因素.3 号线从青岛站到青岛北站，一共22 个站点；首、末班车时间分别为06:00 和23:15，以15 min 等间隔划分，92 d里共划出6 348 个时间步.将前89 d 作为训练集，后3 d作为测试集.

为判断模型预测效果，选用平均绝对误差(MAE，单位：人次)，均方根误差(RMSE，单位：人次)量化分析，误差计算公式为

为验证模型有效性，选取5 个经典模型(ARIMA，SVR，LSTM，CLTFP[10]，ConvLSTM)与ResNet-CNN1D做性能分析.

3.2 模型参数设置

ResNet-CNN1D 模型中，观测时间步长r=5，MAE，RMSprop 分别为损失函数、优化器，学习率为0.000 5.激活函数g(·) 为ReLu，数据在0～1间标准化.二维卷积层的卷积核大小为3×3，一维卷积层的卷积核长度为5，残差单元数量L=4.为保证时间序列的连续性，不使用池化层；为保留边缘信息，采用padding. 使用Python 语言在Keras 和TensorFlow 框架下构建模型，训练过程中使用GPU加速.

对比模型中，所有参数设置都采用调优和对比统一的原则. ARIMA 模型的参数p,d,q∈[0,1,0]～[7,1,5]，并利用网格搜索的方式寻找最优参数. SVR 内核为径向基函数，参数C,ξ,γ∈[1 ,0.05,0.05] ～[1 00,0.25,0.25] ，同样基于网格搜索确定最优参数. LSTM 的输出维度为44，ConvLSTM的卷积核大小为3×3.其余模型均基于ResNet-CNN1D 模型中部分组件，参数设置与ResNet-CNN1D模型保持一致.

3.3 预测精度分析

(1)模型的变体比较.

对ResNet-CNN1D 模型的各组件进行拆分实验，结果如表1 所示. CNN1D 与ResNet 分别作为挖掘时间与空间特征的组件，由于只能学习到单一的特征信息，预测效果不佳；CNN2D(2)-CNN1D与CNN2D(10)-CNN1D 的区别在于二维卷积层的数量不同，10 层的效果优于2 层，即深层卷积网络能更好地捕捉站点间的空间特征，有利于提升预测精度；CNN2D(10)-CNN1D 与ResNet-CNN1D 相比，前者没有采用残差网络的结构，实验证明残差结构的加入，有利于模型优化与精度提升.总之，ResNet-CNN1D不仅能融合时空特征信息，深层网络与残差结构的加入，使模型更充分地捕捉间隔遥远站点间的相关性.

表1 模型组件实验结果Table 1 Experimental results of model components

(2)交通流中经典预测模型比较.

与经典模型对比结果如表2所示，可以发现：

①本文ResNet-CNN1D 模型在进站、出站和总客流量的预测中，均保持最佳预测精度.

② ARIMA 适用于单变量且平稳的时间序列，故只提取20 d 的适用性数据，共计1 380 个时间步，作为模型的初始训练集，以实时更新训练集的方式预测下一时间步，因此，每个站点在预测下一个时间步时，都需要训练一个独立模型；SVR的输入是所有站点前5个时间步的观测数据，输出是单一站点进站或出站的预测结果，故每个站点的进站或出站预测，均需要一个独立模型.与神经网络训练单一模型便可同时预测所有站点的进出客流量相比，ARIMA 和SVR 构建模型较多，调参过程更加复杂.此外，ARIMA 因无法捕捉客流的非线性特征，预测效果较差；SVR虽然解决了非线性问题，但不适用于多变量同步预测的回归问题.

③LSTM 和CLTFP 都是基于序列形式的客流量预测，进站和出站数据需通过拼接方式用一维向量表示，模型不能很好地捕捉进站与出站之间的相关性.ConvLSTM是一种可以挖掘时空特征的LSTM 模型，但随网络深度的增加，模型的训练过程变得十分困难，而浅层的网络结构又无法充分捕捉空间特征.

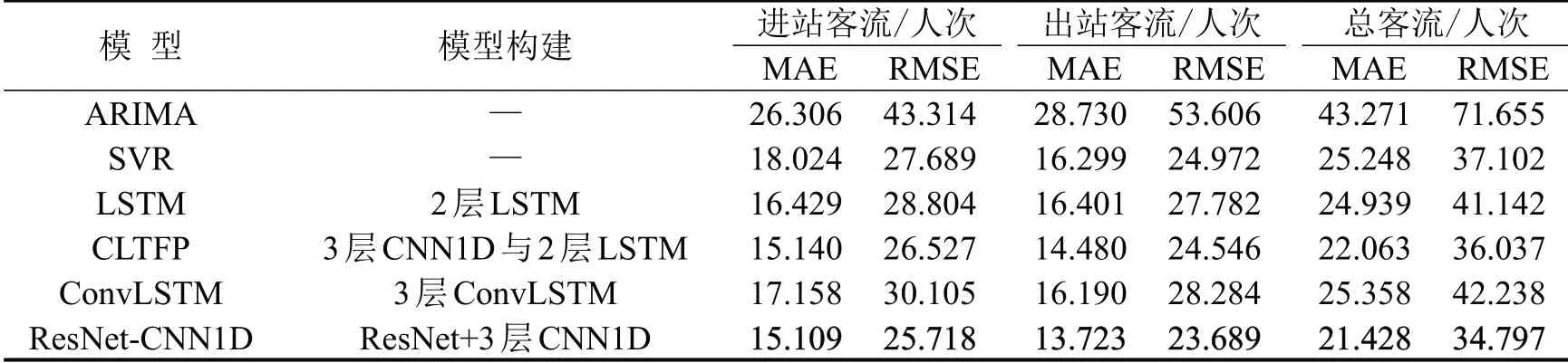
表2 经典模型对比Table 2 Comparisonof classic models

(3)预测结果的可视分析.

为更好展示ResNet-CNN1D模型的预测效果，将10月29日(休息日)和30日(工作日)李村站客流量的真实值与预测值可视化，如图7所示.可知：李村站周日的客流量相对平缓，没有突然的客流高峰期；工作日存在明显的早晚高峰期，早晨是进站高峰，晚上是出站高峰.ResNet-CNN1D 模型可以精准地预测到工作日早晚高峰的客流值，以及周末的多个局部客流峰值.

图7 李村站客流量真实值与预测值对比图Fig.7 Actual and predicted passenger flow of Licun station

3.4 时间分析

将时间特征组件替换成LSTM 网络，构成ResNet-LSTM 模型. LSTM 已经在ST-LSTM[3]与CLTFP[10]模型中被证实具有很好的时间特征的学习能力.如图8 所示，随着残差单元数量变化，ResNet-LSTM 与ResNet-CNN1D 在总客流量预测中，表现出相似的变化趋势.另外，当空间特征组件的深度过浅或过深时，ResNet-CNN1D模型表现出更佳的预测效果.

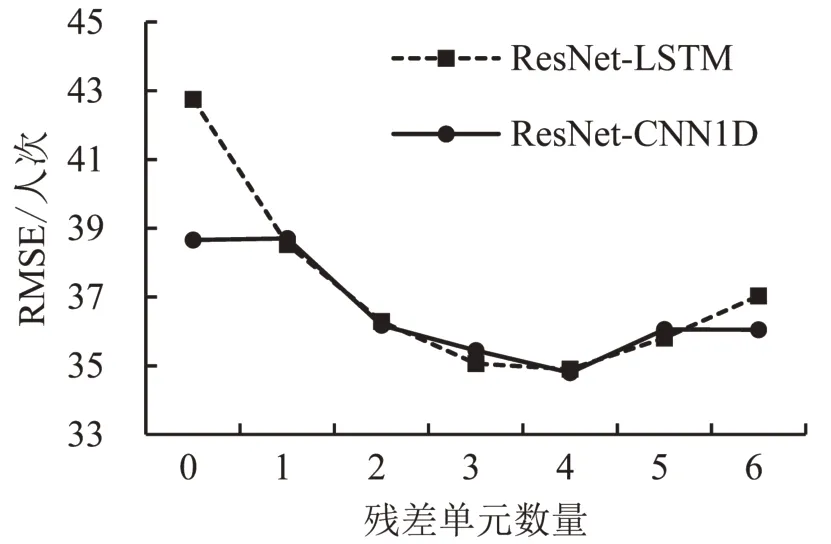
图8 ResNet-LSTM 与ResNet-CNN1D 模型对比Fig.8 Comparison of ResNet-LSTM and ResNet-CNN1D model

如表3 所示，残差单元数量确定为4 后，对比ResNet-LSTM 与ResNet-CNN1D 模型的预测误差可以发现，两模型的预测精度不相上下；但时间消耗方面，ResNet-CNN1D 的训练时间减少了35%.所以，相比于LSTM，CNN1D更适合挖掘地铁客流量的时间特征.

表3 模型对比结果Table 3 Model comparison results

4 结 论

针对多地铁站的短时客流量预测问题，本文提出一个新的端到端混合网络模型，将基于二维卷积的残差网络与一维卷积网络进行结合.二维卷积的特征检测是在站点维度上进行，结合深层残差结构，充分捕捉站点间的空间特征.一维卷积层的特征检测是在时间轴上移动，充分挖掘客流量的时间特征.最后通过加权融合，得到目标时段客流量的预测结果.本文采用青岛市地铁3号线的刷卡数据对模型进行验证，预测结果明显优于常用5种模型.下一步研究将重点考虑多线路地铁客流量的预测问题，进一步挖掘更复杂交通网络中站点间的时空相关性.