多级混合式齿轮箱动态特性分析*

□ 谭 昕

江汉大学 机电与建筑工程学院 武汉 430056

1 分析背景

多级混合式齿轮箱是兆瓦级风力发电机中的关键部件之一,需要承受极大的扭矩,输出极大的传动比,并保持15 a以上的工作寿命。多级混合式齿轮箱的动态特性对工作寿命有重要影响。整个齿轮传动链的传动误差是齿轮箱内部的一个重要激励,当齿轮传动链的刚度表现出非线性特性时,这种内部激励难以控制[1]。如果齿轮传动链动态传动误差的频率与齿轮传动链的某阶模态频率相同或相近,那么齿轮箱将会发生共振,对齿轮箱工作寿命会产生极大影响。可见,研究齿轮箱动态传动误差激励频率与齿轮箱振动模态之间的关系是一项重要工作。

目前,研究主要集中在静强度、固有频率、振动模态分析等方面[2],通常应用集中质量法进行计算[3]。

笔者通过理论计算,推导齿轮传动链动态传动误差的计算方程。采用Pro/E软件对某型多级混合式齿轮箱进行整机三维建模,并将建立的整机三维模型导入ANSYS软件,建立有限元模型[4],通过仿真计算得到齿轮箱整机约束振动模态。将理论计算得到的动态传动误差激励施加到齿轮箱有限元模型上,通过仿真预测整机发生共振的可能性。

2 齿轮箱三维建模

笔者以某型兆瓦级风力发电机多级混合式齿轮箱为例,其结构简图如图1所示。基于相关参数在Pro/E软件中进行三维参数化建模,以.x_t格式文件导入Romaxwind软件,生成整体虚拟样机,加载后通过虚拟仿真运行获得齿轮传动链相关刚度矩阵和位置矩阵。多级混合式齿轮箱三维模型如图2所示。

▲图1 多级混合式齿轮箱结构简图

▲图2 多级混合式齿轮箱三维模型

3 齿轮传动链传动误差建模

传动误差分为静态传动误差Ed和动态传动误差Es两种,两者之间的关系为[5]:

Ed=DT+Es

(1)

式中:DT为静态传动误差Es与动态传动误差Ed之间的补偿值。

DT为:

(2)

式中:[K]为齿轮传动链的时变刚度矩阵;[F]为齿轮传动链的位置矩阵;r为啮合点处的曲率半径;c为阻尼因数;i为总传动比;ψ为正交转置矩阵。

多级齿轮传动链的总传动误差Δθ可以表示为[6]:

(3)

式中:im为第m级传动的传动比,m=2,3,…,N;Δθg为第g级传动的传动误差,g=1,2,…,N。

Δθg为:

(4)

由齿轮传动比误差引起的传递误差函数为:

(5)

式中:Δi12为传动比误差。

Romaxwind软件中有一系列用于接收、处理传动误差的函数包,通过使用这些函数包,并应用式(1)～式(3),可以得到齿轮传动链的动态传动误差曲线,如图3所示。

▲图3 齿轮传动链动态传动误差曲线

齿轮传动链动态传动误差的峰值频率见表1。齿轮传动链的啮合刚度表达式为[7]:

Fh=DhEd

(6)

式中:Dh为动态啮合刚度;Fh为动态啮合力。

表1 齿轮传动链动态传动误差峰值频率

为了获得准确的太阳轮与行星轮啮合刚度变化规律,笔者采用有限元分析软件进行处理。将太阳轮与行星轮系统单独取出,设置行星轮系轴承系统全部为刚性,以滤除轴承变形导致的啮合刚度变化。将行星轮设置为静止,将单个行星轮上承受的扭矩施加在太阳轮上。通过总传动误差计算得到啮合刚度,这一计算步骤在一个啮合周期中将进行数次[8]。

上述方法同样适用于行星轮与齿圈的啮合过程。经过处理后,动态啮合刚度曲线如图4所示。

▲图4 动态啮合刚度曲线

整个齿轮传动链有两组固有频率和模态:① 各组件都旋转时所具有的显式模态;② 只有行星轮旋转,太阳轮、齿圈和行星架都不旋转时的退化模态。描述齿轮传动系统动态特性的关键是了解啮合相位如何激发系统的谐波响应。通常啮合相位起源于行星齿轮啮合的同步性和动态啮合力的周期,如果某个啮合频率激发出某个模态,那么太阳轮、齿圈、行星架也会在该谐波频率下出现共振[9]。

4 齿轮箱振动模态

通常认为激励频率与系统某模态频率的偏差小于10%或成倍数关系时会发生共振,因此了解系统振动模态是控制动态特性的重要前提。由于自由模态是在无载荷、无约束条件下获得的,主要反映的是系统刚度特性,因此笔者直接研究多级混合式齿轮箱的约束模态。约束施加于多级混合式齿轮箱前后端盖及输入输出端轴承上,边界条件为约束前后端盖及输入输出轴承处的全部自由度,采用这种约束设置与实际情况是一致的[10]。

使用兰乔斯算法在ANSYS软件中对多级混合式齿轮箱三维模型进行模态仿真。根据传动误差峰值频率,多级混合式齿轮箱在600～2 300 Hz频段内模态产生共振的可能性最大,因此笔者提取该频段内前十阶振动模态频率进行分析,见表2。

表2 多级混合式齿轮箱前十阶振动模态频率

对比动态传动误差的五个峰值频率可知,三阶至六阶约束振动模态频率与激励峰值频率较接近。与传动误差峰值频率接近的四个振动模态如图5所示。

▲图5 多级混合式齿轮箱振动模态

由图5可知,三阶振动模态是横向扭转振动模态,在该模态下,多级混合式齿轮箱体上所有点的振动方向是一致的,作用在箱体接合部的压力对振动幅度有明显影响。四阶振动模态是横向弯曲振动模态,可由系统中三个平行轴上的时变轴向力激发。五阶振动模态是摆动振动模态,可由太阳轮的动态啮合力激发,模态振幅比较大。六阶振动模态是扭转弯曲振动模态,由于输出轴承受较大的时变弯矩和扭矩,因此通常会产生周期性轴向和径向变形,从而可能激发这一振动模态。

由于多级混合式齿轮箱三阶、四阶、五阶、六阶振动模态频率与传动误差峰值频率很接近,隔离裕度小于10%,因此多级混合式齿轮箱在工作时存在共振风险。若发生共振,振动能量尖峰以905 Hz为主。观察上述四种振动模态可知,多级混合式齿轮箱中段刚度不足是导致振动模态频率偏低的主要原因。多级混合式齿轮箱中段刚度不足的原因包括:① 太阳轮与转轴的连接刚度较低;② 内齿圈结构刚度过低;③ 轴承与轴承座在轴向的支承刚度不足。

为避免发生共振,有两种优化方法:① 改变传动误差激励频率;② 调整结构以改变约束模态频率。由于改变传动误差激励频率相对而言难度更大,因此笔者采用调整箱体结构,进而改变振动模态频率的优化方案。具体措施为:① 缩短全部行星传动中太阳轮主轴长度,对太阳轮与主轴的配合尺寸采用更高精度的公差等级,并采用花键连接太阳轮和主轴;② 适当加大内齿圈宽度和厚度;③ 调整角接触球轴承游隙,以提高支承刚度。

5 试验台架测试

根据上述优化方案重新设计多级混合式齿轮箱,加工等比例实物模型,并搭建多级混合式齿轮箱动态特性试验台架[11],如图6所示。这个测试台架由一台3 kW电机驱动,测试台架上有四个信号采集单元,负载端为磁粉制动器。四个信号采集单元通过专用插槽固定在齿轮箱箱体上以获得振动信号。

▲图6 多级混合式齿轮箱动态特性试验台架

多级混合式齿轮箱箱体上布置四个信号采集点。第一个采集点设置在前齿轮箱盖上,因为这一段箱体结构较复杂,振动模态较多,且承受的载荷较大。第二个采集点设置在后齿轮箱盖上,因为后齿轮箱盖支撑输出轴,应检测其连接刚度。第三个采集点设置在第一级齿轮的轴承附近,以方便测试来自于轴承的激励力信号。第四个采集点设置于输入轴上,以测试输入扭矩的变化。第一个和第二个采集点布置位置如图7所示。

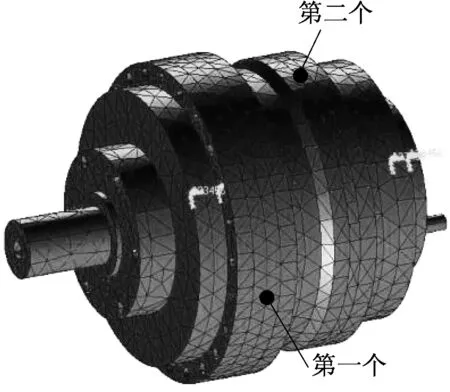
▲图7 多级混合式齿轮箱信号采集点布置位置

由动态试验获得的多级混合式齿轮箱优化后振动模态频率见表3,试验测得多级混合式齿轮箱在600～2 300 Hz频段内共有六个振动模态频率。与表1比较可以发现,多级混合式齿轮箱结构优化后的振动模态频率与动态传动误差峰值频率相差较大,且在动态传动误差一阶谐波作用下的频率响应峰值与动态传动误差自身的频率完全不同,发生共振的可能性明显降低。

表3 优化后多级混合式齿轮箱振动模态频率

另一方面,在动态传动误差高阶谐波作用下的频率响应峰值与动态传动误差自身的频率也完全不同。由此可以得出结论,经过结构优化后的多级混合式齿轮箱在自身动态传动误差的激励下发生共振的可能性很小。

6 结束语

笔者通过计算机软件仿真分析与试验相结合的方法,研究多级混合式齿轮箱动态特性,具有效率高、结果准确的特点。这一方法在Pro/E、ANSYS、Romaxwind三个通用软件中进行,具有数据交换方便、结果精度高的优势,对齿轮箱类机械系统动态特性的确定具有较好的适用性。

通过研究发现,对于齿轮箱类机械系统而言,在结构设计时应注意两方面问题。

(1) 不能仅考虑系统输入、输出产生的振动激励,齿轮箱内部传动误差引起的振动激励也非常重要。在模态分析时,不仅要研究自由模态,而且应考虑约束模态对系统动态特性的影响。

(2) 应充分应用动态试验来研究齿轮传动系统的共振频率,并以此作为结构设计改进的依据。尤其应考虑各结构件连接刚度对共振频率的影响,尽可能使约束模态频率避开共振激励频率。