有效数字的“有效”解读

孙海源

摘要：实验学科中，实验数据的记录与处理有着非常重要的作用。在记录与处理实验数据时，常会遇到有效数字相关的问题。教学“化学实验数据的处理”时，可从有效数字的作用、位数确定方法、运算规则等方面，“有效”解读有效数字。

关键词：有效数字 实验数据处理 运算规则

实验学科中，实验数据的记录与处理有着非常重要的作用。在记录与处理实验数据时，常会遇到与有效数字相关的问题。有效数字是指实际能够测量到的数字，包括最后一位估计的、不确定的数字。我们把通过直读获得的准确数字称为可靠数字，把通过估读得到的数字称为存疑数字，把测量结果中能够反映被测量大小的带有一位存疑数字的全部数字称为有效数字。

笔者在教学“化学实验数据的处理”时，重点突出了对有效数字的解读：首先，引导学生认识有效数字的重要性，探讨“处理数据时，不考虑有效数字会出现什么结果”;接着，建构有效数字位数确定的方法，帮助学生深刻理解有效数字的定义;最后，分析有效数字的运算规则，促进学生形成对有效数字的全面认知。具体教学过程如下：

一、认识有效数字的重要性

教师出示如下信息：

己烷（C6H14）存在5种同分异构体，均为液体，其结构与密度数据如下页表1所示。现有一瓶己烷液体，没有标出是哪种同分异构体。同学A用测量密度的方式确定其成分：用量筒量取了5.0 mL的该液体，使用分析天平称量出其质量为3.2745 g。

并提问：

根据信息中的数据，该液体密度d=mV=3.2745 g5.0 mL=0.6549 g/mL，所以是3号液体，对吗？

大部分学生认同这一观点，但仍有一些学生提出了质疑：这个数据看起来好像跟1号液体的密度也很接近，万一是数據不够精确导致的呢？万一该液体的体积不是刚刚好5.0 mL或者质量不是刚刚好3.2745 g呢？因为确实存在不同的学生在读取同样的位于量筒中的水的体积时得到的数据不一致的情况。学生自然讨论起来：“该液体的体积V与质量m均不是准确的数值，而是存在一定误差的。这个误差可能是读数引起的，也可能跟仪器本身的精度有关。”“V=5.0 mL，代表其体积可能正好是5.0 mL，也可能是5.1 mL，或者4.9 mL，即5 mL左右。”“V=5.0 mL中最后一位的‘0是不准确的，存在一定的误差;同样的，质量m=3.2745 g中的最后一位数字‘5也是不准确的。”

对此，教师引导：为了方便分析，我们不妨假设体积和质量均在最后一位产生“1”的误差，即体积V的真值范围是（5.0±0.1）mL，质量m的真值范围是（3.2745±0.0001）g。

学生据此计算得到该液体的密度范围，即密度的最小值dmin=（3.2745-0.0001） g（5.0+0.1） mL=0.6420 g/mL，最大值dmax=（3.2745+0.0001） g（5.0-0.1） mL=0.6683 g/mL。

可以看到，该液体的密度（单位：g/mL）在0.6420到0.6683之间，也就是说，该液体的密度在小数点后第2位就已经不准确了。那么，一开始计算得到的“准确值”0.6549也就不是准确值了，在第2位的“5”上面就已经有变化了，0.6549可能是0.6420，也可能是0.6683。既然这样，还有必要把该液体的密度写这么多位吗？既然0.6549中的“5”已经不准确了，后面的“49”还有意义吗？这么一讨论，学生会发现：原来只能保证计算数据中的“0.6”部分是确定的，而小数点后面第2位的“5”就已经存在不确定性了，那么计算时只需要保留到这一位就可以了，即d=mV=3.2745 g5.0 mL=0.65g/mL。显然，这个计算结果无法确定该液体的类型。

顺着这个思路，学生发现，之所以不能确定结果，是因为测量太粗糙了，尤其是使用量筒来测量体积，误差太大了。教师顺势提问：那么，如果我们能够把体积测量得更加精确呢？假如同学B此时选用带刻度的移液管测量该液体体积，得到的体积数据为V=4.93 mL，其误差也产生在最后一位，同样为±0.01，此时我们能够确定该液体是几号液体吗？

经过与上面类似的计算过程，得到d=mV=3.2745 g4.93 mL=0.6642 g/mL，dmin=（3.2745-0.0001） g（4.93+0.01） mL=0.6628 g/mL，dmax=（3.2745+0.0001） g（4.93-0.01） mL=0.6656 g/mL。

这时，学生发现，能够保证准确的数据多了一位，而不确定的数据则是小数点后第3位及以后的数。对比表1中的密度数据，学生发现，该液体是5号液体。此时，有效数字的“效”就显现出来了——其对于实验结果的确定十分重要。

二、建构有效数字位数确定的方法

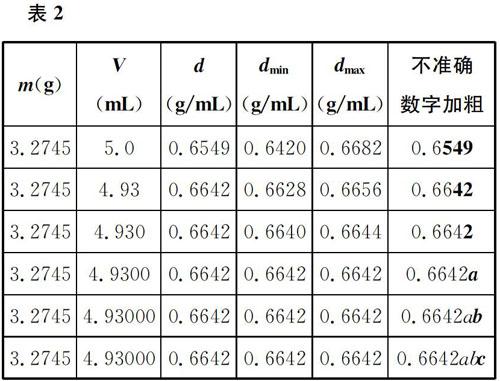
在教学过程中，细心的学生发现：密度计算结果中不确定数字的位置与体积、质量测量结果中不确定数字的位置是相关的。为了验证这一点，教师引导学生将体积测量值的有效数字推广到更多的位数（其计算结果如表2所示）。

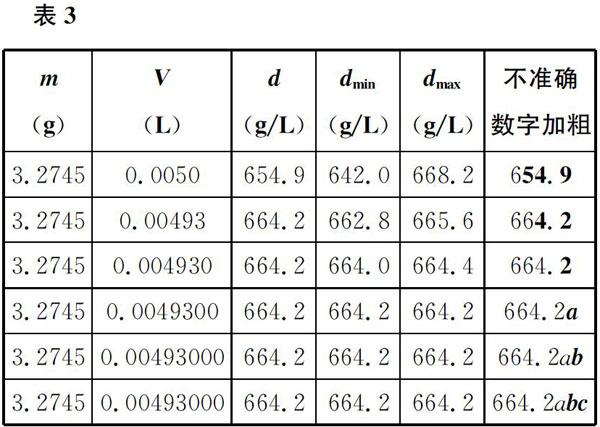
那么，可以使用什么方式描述这种位置？有学生指出：可以使用小数点后第几位的描述方式。但是，稍加讨论就发现，这种方式好像不那么“正确”，因为如果把体积的单位调整为L，密度的单位相应地变为g/L，会有如表3所示的结果。因此，学生发现，使用该数据位于非零数字后面的位数更加合适。这样的讨论过程其实就是建构有效数字定义的过程。

三、分析有效数字的运算规则

更进一步地，学生把三个物理量数据的有效数字位数统计出来（如表4）后发现，有效数字在进行除法运算时似乎遵循如下规则：当体积的有效数字位数小于质量的有效数字位数时，密度的有效数字位数与体积的有效数字位数相等;当体积的有效数字位数等于或者大于质量的有效数字位数时，密度的有效数字位数就保持在质量的有效数字位数，即两个数据相除，商的有效数字的位数似乎取决于有效数字位数较少的那个数据。