基于MIDAS软件的大跨钢箱梁吊装力学性能分析
潘龙文,叶丽宏
(1.杭州西湖城市建设投资集团有限公司,浙江 杭州 310013;2.浙江工程建设管理有限公司,浙江 杭州 310012)
人行天桥又称人行立交桥,只能允许行人通过,可有效避免车流和人流平面相交时的冲突,保障人们能够安全地穿越,提高车行速度,减少交通事故的发生。钢结构体系具有自重轻、安装容易、施工周期短、抗震性能好、投资回收快、环境污染少等综合优势,我国钢结构工程市场前景非常广阔[1]。钢箱梁吊装涉及设计和施工安全问题,特别是振频大小对挠度的影响性如何,对吊装时的钢箱梁人行天桥的结构安全性和舒适性至关重要。本文基于Midas软件进行不同工况下的临时支撑架静力验算及上部结构验算,并运用数理统计方法分析最大压应力、最大拉应力、挠度、振频等技术参数的关系,探讨出挠度和振频之间存在显著线性相关性的结论,从而为指导大跨钢箱梁吊装设计和施工安全技术提供了重要理论依据,并且对类似钢箱梁设计和施工均具有一定的借鉴意义。
1 工程概况
本项目位于钱江世纪城核心区临江地块,北侧过钱塘江是钱江新城,西侧与奥体中心相邻,南侧是滨江高新技术开发区,东侧可达萧山国际机场,是杭州南向发展带上的重要节点。观澜路人行天桥为跨越澜路连接T字形横向与竖向的人行通道,桥位场地位于萧山钱江世纪城观澜路南北侧,全长193 m,分为五联,钢结构部分共五联,第一联至第五联长度分别为20、48、25、35、65 m,设计使用年限50年,钢箱梁均采用Q345C材质。见图1、图2。
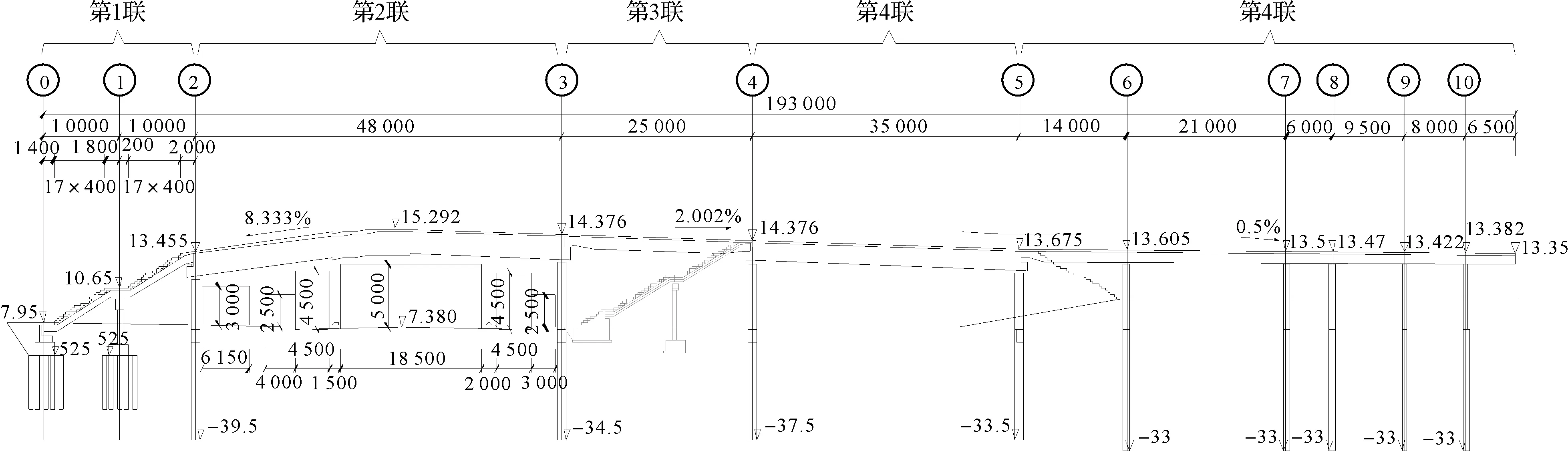
图1 观澜路人行天桥工程立面

图2 观澜路人行天桥工程航拍
2 钢箱梁吊装工况分析
2.1 150 t汽车吊吊装工况分析
钢箱梁梁段最大重量为71.6 t,采用2台150 t汽车吊抬吊吊装,抬吊时每台吊机吊装重量为71.6÷2÷0.75(考虑0.75的折减系数)=47.7 t。当150 t汽车吊主臂长25.6 m,工作半径为10 m时,起重量为50 t,而钢箱梁梁段抬吊时单机起重量为47.7 t,满足吊装要求。
2.2 25 t汽车吊吊装工况分析
挑臂梁最大重量为7 t,采用2台25 t汽车吊抬吊吊装,抬吊时每台吊机吊装重量为7÷2÷0.75(考虑0.75的折减系数)=4.6 t。当25 t汽车吊主臂长20.5 m,工作半径为5.5 m时,起重量为9.5 t,而挑臂梁梁段抬吊时单机起重量4.6 t,满足吊装要求。
3 钢箱梁吊装工艺和顺序
3.1 钢箱梁吊装工艺
钢箱梁吊装工艺见图3。
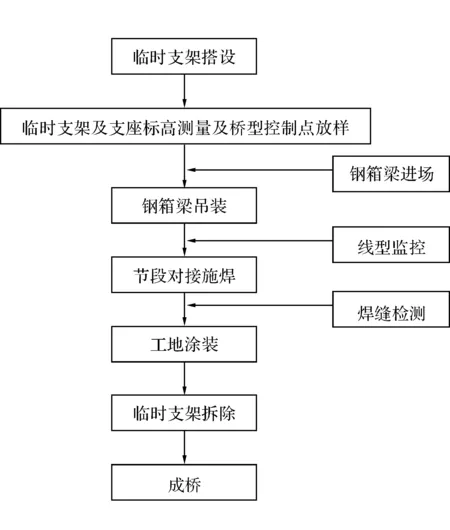
图3 钢箱梁吊装工艺流程
3.2 钢箱梁吊装顺序
先施工第二、第四联的钢箱梁,接着施工第三、第一联的钢箱梁,最后施工第五联的钢箱梁,匝道穿插进行安装施工。各联内安装施工顺序按照编号依次进行,总体遵循从中间往两侧的安装施工思路。钢箱梁采用双机抬吊的方法进行安装,梁段纵向安装顺序为先中跨后边跨,梁段横向安装顺序为先中间后两边。吊装前需对现场场地进行相应的硬化,以满足吊机的站位。梁段横向吊装顺序为先中间后两边,主要有以下几个步骤(图4):

图4 钢箱梁吊装现场照片
1)在临时支撑架分配梁上标出道路中心线、轴线和分块钢箱梁底板边线,并在边界设置焊接限位装置;2)吊装横向中间第1块钢箱梁;3)吊装横向中间第2块钢箱梁。落梁就位后调整焊缝间隙,在梁块之间纵缝位置用码板固定,对焊缝进行点焊;4)吊装一侧的挑臂钢箱梁。挑臂梁就位后调整焊缝间隙,在梁块之间纵缝位置用码板固定,且码板与顶板的焊缝全部焊接好后方可松钩;5)吊装另一侧的挑臂钢箱梁。挑臂梁就位后调整焊缝间隙,同样在梁块之间纵缝位置用码板固定,且码板与顶板的焊缝全部焊接好后方可松钩。
4 Midas Civil软件运用
4.1 Midas Cicil软件
Midas Civil 软件作为通用的空间有限元分析软件和桥梁软件的完美结合,广泛地应用于土木工程领域多种结构的设计与分析,如钢结构、钢筋混凝土结构、预应力混凝土结构[2]。运用Midas软件进行不同工况下的临时支撑架静力验算及桥梁上部结构验算,并对验算数据进行数理统计分析,为钢箱梁结构设计和施工安全提供了重要的理论依据。
4.2 临时支撑架静力验算
临时支撑架材料:钢管采用Φ450×20,材质为Q345B.分配梁采用双拼HM600×300×14×23,横撑、斜撑采用14#槽钢,材质均为Q235B。
4.2.1 最不利组合1:单边加载
F′=(15+124+124+15)/(2×13)=10.7 t,最大等效应力19.8 MPa,最大竖向变形0.652 mm。
4.2.2 最不利工况2:两边加载
F′=(15+124+124+15)/(2×13)=10.7 t,F″=(13+120+120+14)/(4×13)=5.13 t,最大等效应力19.8 MPa,最大竖向位移0.643 mm。
4.3 桥梁上部结构计算
4.3.1 结构计算分析
结构计算分析图(以第一联第一跨为例,其余图略)见图5。

图5 结构计算分析
4.3.2 计算结果及分析结论
1)计算结果
上部结构计算结果见表1。
由表1可知,标准值组合下钢箱梁最大压应力的最大值为70.3 MPa,最大拉应力的最大值为67 MPa,均小于规范规定的钢材容许应力210 MPa,故最大压应力和最大拉应力满足规范要求。
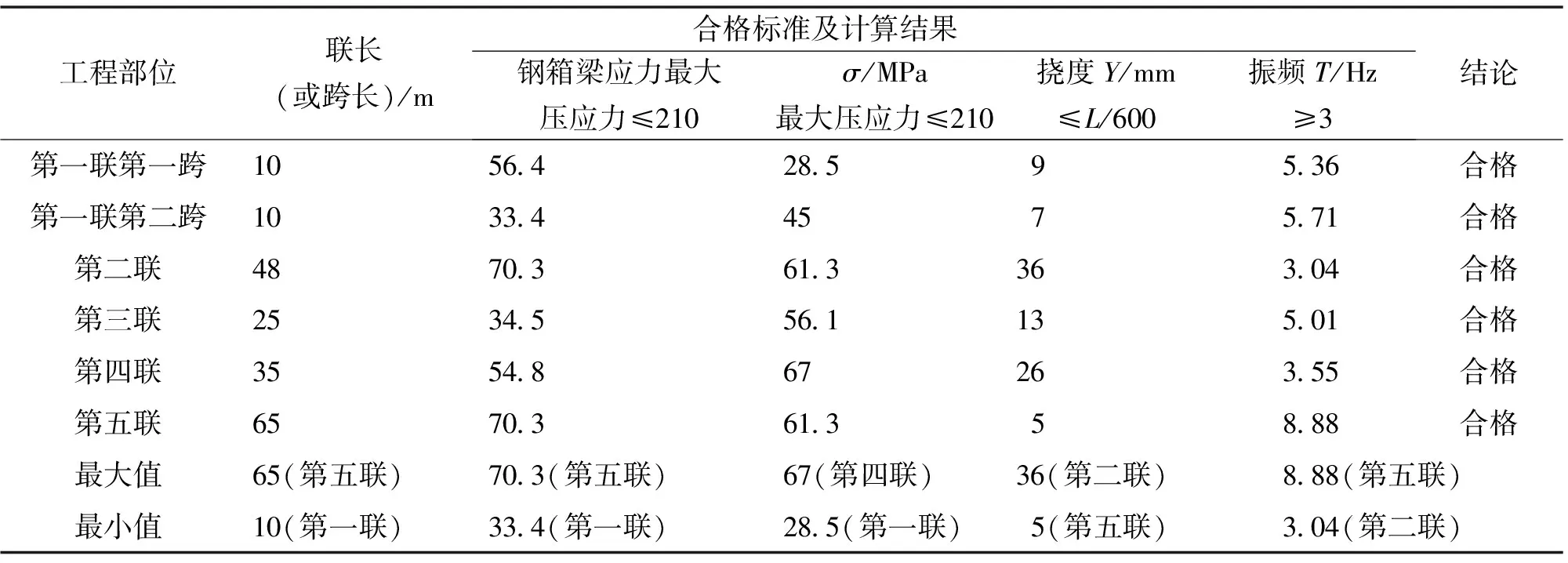
表1 上部结构计算结果
桥梁在活载引起的竖向挠度分别为9、7、36、13、26、5 mm,其挠度允许值分别为:
9 mm 36 mm 26 mm 故挠度满足规范要求。 表1中第二联最小振频3.04 Hz>3 Hz,故振频满足规范要求。 据饶波研究成果,结构自振频率随梁高的增高、基础刚度及墩刚度增大而增大,箱梁底缘宽度对结构自振频率影响不大[3]。当桥梁自振频率与行人步行频率较接近时,会引起主梁振动和挠度过大使行人感到不适并危及天桥的安全。《城市人行天桥与人行地道技术规范(CJJ 69—95)》规定:为了避免共振,减少行人不安全感,天桥上部结构竖向自振频率不应小于3 Hz[4]。 2)分析结论 运用回归方程显著性检验F检验法[5],根据回归分析研究,在联长、最大压应力、最大拉应力、挠度、振频5者中,只有挠度和振频两者的回归是显著的,其余两两之间不显著。其中挠度和振频回归分析见表2。 表2 挠度与振频关系 运用SPSS数理统计分析软件,计算结果见表3、表4: 表3 挠度与振频回归统计 表4 挠度与振频方差分析 F=8.796 557,a=0.05,Fa(1,4)=7.71,F=8.796 557>Fa(1,4)=7.71,回归是显著的。 运用SPSS软件计算出的回归系数分别为a=42.084,b=-4.960,则一元线性回归方程为y=42.084-4.960x(x为振频,y为挠度);再用WPS2019软件进行数理统计回归分析验证,所得回归方程与上述完全一致,挠度与振频相关性见图6。 图6 挠度与振频相关性 以上说明:挠度和振频之间存在显著线性相关性。即挠度与振频呈拟合线性反比关系,振频越大,挠度越小;振频越小,挠度越大。根据《城市人行天桥与人行地道技术规范(CJJ 69—95)》规定:为了避免共振,减少行人不安全感,天桥上部结构竖向自振频率不应小于3 Hz。故在钢箱梁设计验算中,可使设计的钢箱梁结构自频振率较大(至少大于3 Hz),则桥梁在挠度方面的性能较为有利。另外,行人在钢箱梁上行走振动频率为1.8~2.5 Hz,施工时振频较小(最高不超过3 Hz),则不会与钢箱梁结构自振频率保持一致,从而减少共振风险。当然,还可运用调频质量阻尼器(TMD)减振系统削减人行天桥的共振反应,共振情况下减振率接近70%,提高了桥梁结构的安全性和舒适性[6]。 本文初步进行了大跨钢箱梁吊装力学性能分析,采用Midas Civil软件进行不同工况下的临时支撑架静力验算及桥梁上部结构验算等,并运用SPSS软件分析研究最大压应力、最大拉应力、挠度、振频等技术参数的关系,主要有以下结论: 1)挠度和振频之间存在显著线性相关性,回归方程为:y=42.084-4.960x(x为振频,y为挠度)。即振频越大,挠度越小;振频越小,挠度越大。 2)除挠度和振频之间外,最大压应力、最大拉应力、挠度、振频等两两之间不存在显著性相关性。 3)在钢箱梁设计时,大跨钢箱梁结构自振频率大于3 Hz较为有利;而在钢箱梁施工过程中,振动频率较小(最高不超过3 Hz)可有效避免共振的安全风险。 4)可运用调频质量阻尼器(TMD)进行有效的结构减震。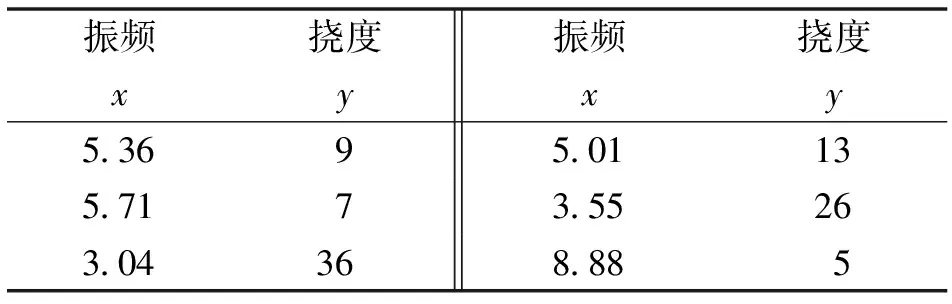



5 结 语

