导弹部队作战单元作战效能评估研究∗

（火箭军工程大学 西安 710025）

1 引言

随着使命任务的拓展，导弹部队将以武器系统为基础集成指挥控制、侦察通信、转载测试和综合保障等能力要素形成作战单元，以作战单元为基本作战单位跨战区遂行多种样式的作战任务，将成为未来战场上的新常态。导弹部队作战单元的作战效能是该作战单元在预期或规定的作战使用环境以及所考虑的组织、战略、战术、生存能力和威胁条件下，完成规定任务的能力[1]，是完成作战任务的度量。但是进行效能评估时，因评估人员所处的地位不同、观察的角度不同，对许多系统评估问题持有不同的理解[2]。如何有效评估该作战单元的作战效能，是准确获得部队使用导弹装备综合作战能力的重要参考、对促进部队战斗力生成具有重要的意义和作用。本文以某型导弹武器系统集成后的作战单元作为研究对象，建立合适的指标体系，采用灰色评估方法实现其作战效能的准确评估，为该型装备作战运用提供决策依据，为未来大规模联合作战奠定重要基础。

2 导弹作战单元作战效能指标体系构建

作战效能指标作为作战行动方案的决策依据和作战单元作战能力的评价标准，在分析导弹作战单元作战效能中占有至关重要的地位。作战效能指标的设计和指标体系的构建是作战效能评估的基础性工作，也是核心工作，其直接关系到评估结果的合理性、准确性[3]。

2.1 指标体系构建原则

导弹部队作战单元作战效能评估应当以其功能、组成和任务为出发点，确定其指标体系应遵循以下原则：

1）系统性原则。指标体系应能较客观反映作战单元的特点和结构，并充分考虑各指标之间的联系和影响，各个指标覆盖范围要广，全面体现导弹部队作战单元的作战效能。

2）实战性原则。构建指标体系必须将武器装备、人员环境置于一定作战背景下，以导弹部队作战单元在作战想定下的使命任务为依据，从而为评估指标体系拟定奠定基础。

3）可行性原则。建立指标体系应当考虑各指标的可获取性以及可度量性，确保其便于采集、分析和处理。否则，不但会加大评估难度，而且可能导致评估结果不可信。

2.2 导弹作战单元作战效能指标体系

通过分析一个作战单元的装备、人员配置，设定特殊作战环境和完整的作战任务剖面，确定作战单元作战效能目标层为生存能力、通信能力、打击目标能力、作战指挥能力、综合保障能力五个方面为一级指标。各一级指标又可用诸多具体指标来衡量，建立二级指标，具体的指标体系如图1所示。

3 导弹部队作战单元作战效能评估

3.1 权重指标的确定

在效能评估中，确定各指标的权重是计算评估结果重要最的一个内容，权重的合理与否将会影响评估结果的准确性。在实际效能评估应用中，应当兼顾各种方法的优缺点，使得效能评估的结果更加符合客观情况[4]。

3.1.1 层次分析法确定二级指标权重

层次分析法（Analytical Hierarchy Process，AHP）是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法[4]。层次分析法用决策者的经验判断各衡量指标能否实现的标准之间的相对重要程度，通过两两比较、判断和计算，以获得各个要素的权重。由于篇幅有限，本文以U1指标为例，采用层次分析法，确定二级指标权重。

1）构建判断矩阵，计算权重向量

根据指标U11U12U13对U1的重要性，将U1层两两比较，填写表格，构造判断矩阵。

表1 判断矩阵和权重向量

则U1层权重向量w1=(0.540，0.297，0.163)。

2）一致性检验

（1）计算判断矩阵的特征根

（2）一致性指标判定

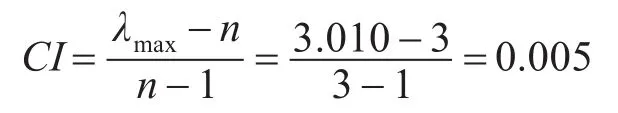
由于该判断矩阵为3阶矩阵，查表可得其平均随机一致性指标RI=0.58。

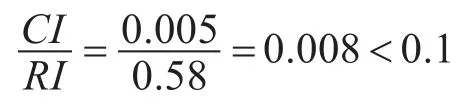
因此判断矩阵完全满足一致性检验要求，故U1层权重w1=(0.540，0.297，0.163)符合要求。

按照同样的计算方法，可以计算出：

3.1.2 G1赋权法确定一级指标权重

层次分析法是确定评价指标的重要方法，但是对于指标过多，进行两两比较时容易出现错误，采用G1赋权法可以避开层次分析法的弊端，无需构造判断矩阵，减小了权重求解的计算量；同时，G1赋权法所确定的关系也来自评价专家，也具有较高的可信度。

1）确定指标间的重要性

采用专家评定，确定指标重要程度，并按照重要性进行排序：U3≥U1≥U2≥U4≥U5。记xn*为排序后的第n个指标，则x*≥x*≥x*≥x*≥x*，由x*12345n与 Ui的对应关系可得，x1*=U3，x2*=U1，x3*=U2，x4*=U4，x5*=U5。

2）确定权重比

相邻两个指标之间的权重之比表示为rk，即，其取值参考表2。通过专家打分结果，可得r2=1.2，r3=1.2，r4=1.4，r5=1.6。

表2 G1赋权法指标间重要性比较

3）确定权重系数

指标xn*的权重记作w*n，其计算公式为

首先计算w*5=0.093，根据可得

同理求得w*3=0.208，w*2=0.250，w*1=0.300。由xn*与Ui的对应关系，可得一级指标权重w=(0.250，0.208，0.300，0.149，0.093)。

3.2 确定评估标准，建立样本矩阵

为实现对作战效能的综合评价，需将各定性指标转化为定量指标，根据实际情况制定相应的评分等级标准（见表3），其中f为评分值。

表3 评分等级标准

按照评分标准，选取五位专家对各项指标进行评分，各指标评分结果见表4，所有得分dijk组成评价样本矩阵。

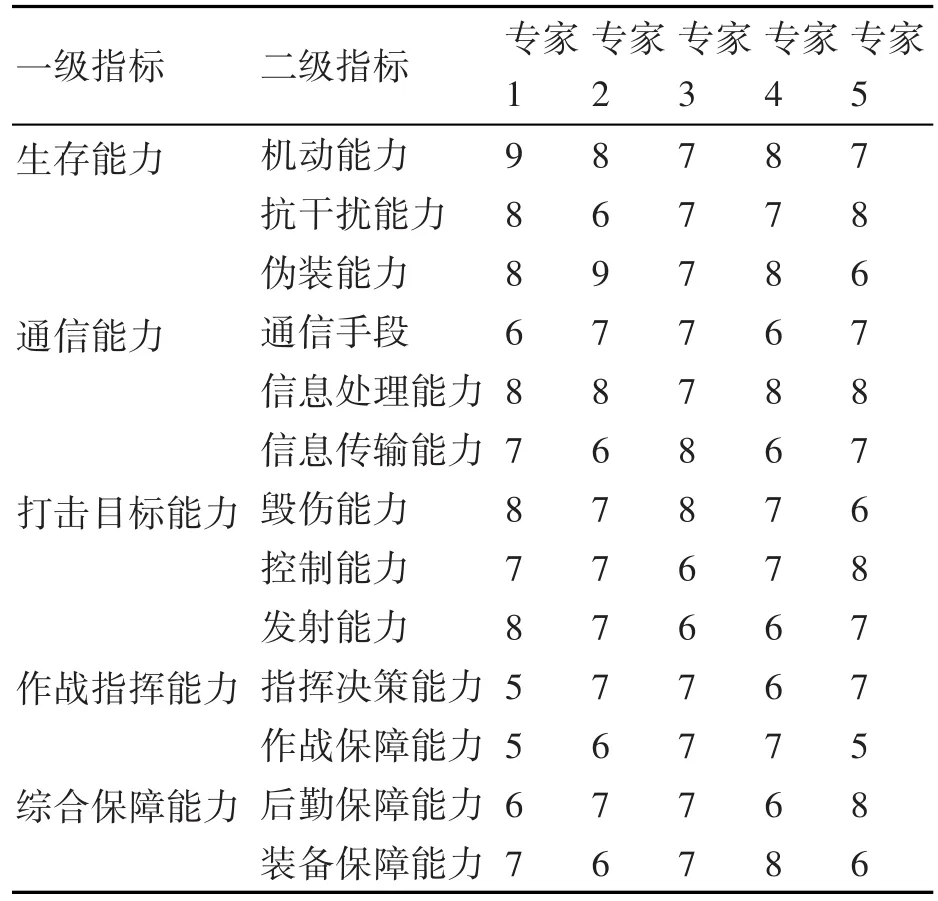
表4 各指标评分结果

3.3 计算灰色评价权向量及矩阵

根据灰色评估理论，确定评价灰类e=1，2，…，g，即要确定评价灰类的等级数、灰类的灰数⊗及其白化权函数fe(dijk)。

3.3.1 确定评估灰类

第一灰类“优”（e=1），灰数 ⊗1∈[0，8，∞]，白化权函数为

第二灰类“良”（e=2），灰数 ⊗2∈[0，8，16]，白化权函数为

第三灰类“中”（e=3），灰数 ⊗3∈[0，4，8]，白化权函数为

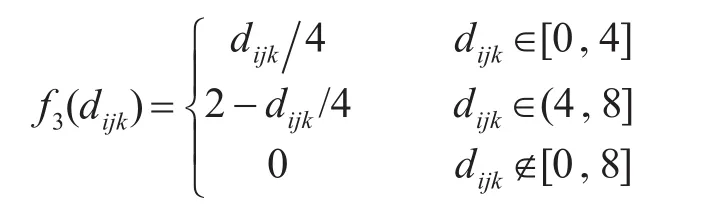
第四灰类“差”（e=4），灰数 ⊗4∈[0，2，4]，白化权函数为

3.3.2 计算灰色评价系数

以生存能力U1为例，计算灰色评价权向量及矩阵：

各评价灰类的总评价系数记为x11，其计算公式为

第e个评估灰类的灰色评价数记为r11e，则有：

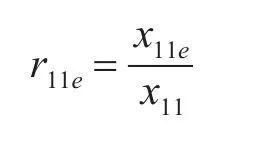
计算得出：r111=0.481，r112=0.468，r113=0.051，r114=0。

3.3.3 计算灰色评价向量及矩阵

U11对各灰色的灰色评估权向量为

同理可得 r12，r13。

利用相同的方法计算：

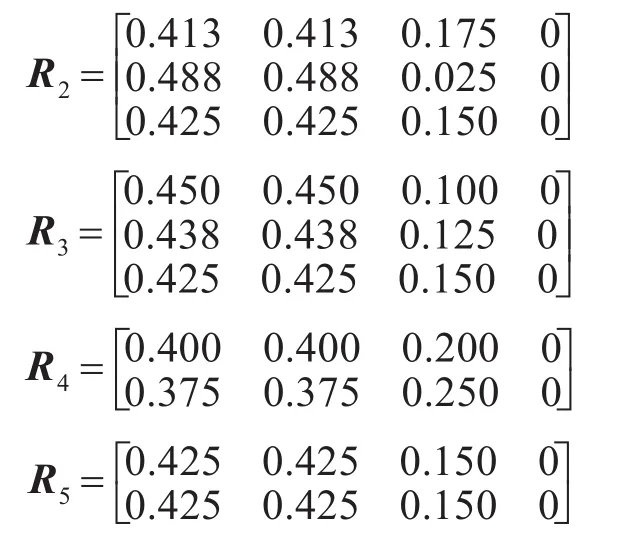
3.4 导弹部队作战单元作战效能的灰色综合评价

首先对Ui作一级综合评判：

利用同样的方法计算：

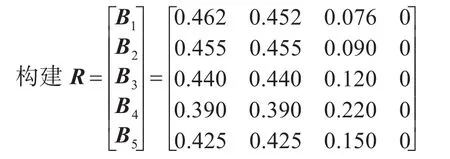
U的二级综合评判结果为

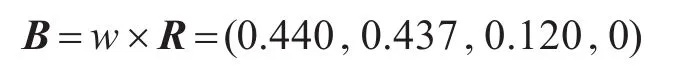
取优、良、中、差对应标准中的值作为各评价灰类等级的值化向量，则值化向量：D=[9 7 5 3]。

进而计算出该导弹部队作战单元作战效能的综合评价值：E=B×DT=6.988。结合评分等级标准（表3）来看，6＜6.988＜8，说明该型作战单元作战效能属“良”类，与实际情况相符。

4 结语

以导弹部队作战单元为单位，通过分析其装备、人员组成，构建了导弹部队作战单元作战效能评估指标体系，并结合指标体系选取适当的赋权法获得权重，最后利用灰色综合评价法对导弹部队作战单元作战效能进行评估。通过对该作战单元作战效能的准确评估可为导弹部队制定科学的作战理论、作战原则和使用策略提供决策依据，能够为导弹部队作战单元在未来跨战区遂行多种样式的作战任务中提高作战能力提供参考。