例谈构造平行四边形解题
葛长岭 朱记松

平行四边形(含特殊平行四边形)是几何图形的重要组成部分,也是中考的必考内容之一,几何中的许多问题,若转化为平行四边形(含特殊平行四边形)问题,借助平行四边形(含特殊平行四边形)的边、角、对角线的性质解决,则可以化难为易,事半功倍.这一“转化”过程,通常是通过添加适当的辅助线,来构造平行四边形(含特殊平行四边形).
一构造一般平行四邊形
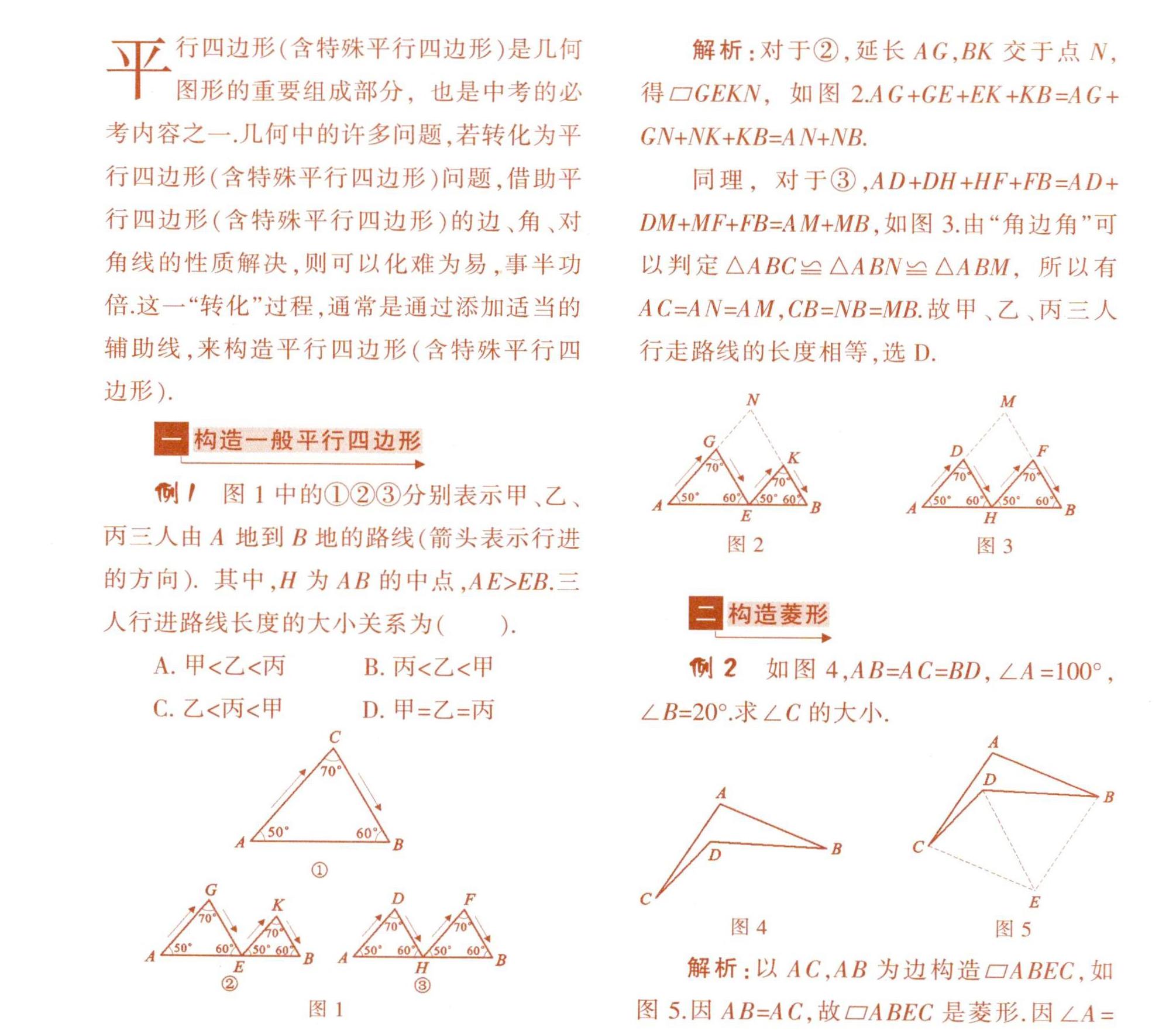
例1图1中的①②③分别表示甲、乙、丙三人由A地到B地的路线(箭头表示行进的方向).其中,H为AB的中点,AE>EB.三人行进路线长度的大小关系为(
).
A.甲<乙<丙
B.丙<乙<甲
C.乙<丙<甲
D.甲=乙=丙
解析:对于②,延长AG,BK交于点N,得□GEKN,如图2.AG+GE+EK+KB=AG+GN+NK+KB=AN+NB.
同理,对于③,AD+DH+HF+FB=AD+DM+MF+FB=AM+MB,如图3.由“角边角”可以判定△ABC≌△ABN≌△ABM.所以有AC=AN=AM,CB=NB=MB.故甲、乙、丙三人行走路线的长度相等,选D.
二构造菱形
例2如图4,AB=AC=BD,∠A=100°,∠/B=20°.求∠C的大小.
解析:以AC,AB为边构造□ABEC.如图5.因AB=AC,故□ABEC是菱形.因∠A=100°,故∠ABE=∠ACE=80°.因∠B=20°.故∠EBD=80°-20°=60°.又AB=BD,AB=BE,则BD=BE,△BED是等边三角形,∠BED=600.所以∠DEC=∠BEC-∠BED=100°-60°=40°.而CE=BE=DF,所以∠ECD=180°-40°/2=70°.所以∠ACD=80°-70°=10°.即为所求.
三构造矩形
例3如图6所示,CD∥AF,∠CDE=∠BAF,AB⊥BC.∠BCD=124°.∠DEF=80°.求∠AFE的度数.
解析:构造如图7所示的矩形GHMN.∠BCD=124°.可求得∠1=56°.∠G=∠H=90°.∠1+∠GBC=90°.AB⊥BC, ∠ABC=90°.因∠2+∠GBC=90°,故∠1=∠2.∠CDE=∠BAF=∠2+∠H=146°.因六边形ABCDEF的内角和为720°,∠DEF=80°,所以∠AFE=134°.
点拨:要求∠AFE的度数,关键是求∠CDE,∠BAF的度数.由CD∥AF,AB⊥BC,联想到“一线三直角”模型,通过构造矩形,将六边形问题转化为平行四边形中的矩形问题.事实上,若注意到CD//AF,∠CDE=∠BAF,通过延长AB,DC及AF,DE,构造平行四边形,同样可以使问题解决.
- 中学生数理化·八年级数学人教版的其它文章
- 陶哲轩:数学不只是严密和证明
- 平行四边形与三角形
- 当角平分线邂逅平行四边形
- 如何构造三角形中位线
- 妙用斜边中线定理
- 矩形面积的特殊求法

