基于旋转水槽试验的水下泥石流底部水压研究*

邓检良 张向霞

(①上海交通大学船舶海洋与建筑工程学院，上海 200240，中国)(②上海城建设计研究院，上海 200125，中国)

0 引 言

水下泥石流中影响最大的是海底泥石流。海底滑坡-泥石流的研究随着海洋油气资源的开发逐渐成为热点。从2003年开始关于海底滑坡-泥石流的国际会议“Submarine Mass Movements and Their Consequences”已经在欧美日本等发达国家连续举办八届，会议交流的主要成果是海洋工程地质现场勘察方面的成果(Duinen et al.，2014)。大量的调查结果(Blasio et al.，2006)表明，海底滑坡-泥石流的等价摩擦系数(滑坡顶部最大高度Hmax和最大水平距离Lmax之比)(张倬元等，2009)介于0.001和0.2之间，对应的视摩擦角β(Hsü，1975)在0.05°到11°之间，而且输送颗粒物的规模越大，其运动阻力越小。我国海底滑坡-泥石流的研究对象集中在黄河口、东海和南海北部，取得了大量研究成果(贾永刚等，2000；刘保华等，2005；胡光海，2010；吴时国等，2011)。

实验研究方面，针对海底泥石流的低阻力运动现象有大量的野外调查和实验研究(Blasio et al.，2006；Elverhoi et al.，2010；Deng et al.，2017；范宁等，2018；鲁晓兵等，2019)。然而，在稳定运动状态下，在非常缓的斜坡上实验再现水下泥石流或海底泥石流非常困难：尽管进行了大量的水槽试验，也没有成功地实验再现(Elverhoi et al.，2010)。水槽试验没有再现低阻力运动现象的原因可能与泥石流形成近似稳定运动状态的条件有关：在斜坡上运动的泥石流很难达到近似稳定状态；并且，如果斜坡角度缓和，那么达到近似稳定状态所需的斜坡长度可能非常大。近年，Deng et al.(2017)采用了旋转水槽的方法，该方法的特点是通过水槽的旋转模拟出无限长的斜面。通过该方法，制作低视摩擦角(约为1°)的稳定运动的水下泥石流取得了成功，为进一步的实验研究开辟了新的实验途径。

海底泥石流理论上的一大难点是对低阻力运动的机理解释。目前，比较流行的假说是滑水假说(Talling et al.，2007)，在忽略泥石流本身的强度和黏滞性的情况下，认为低阻力运动与滑水有关，然而，滑水过程只能抬升水下泥石流的前缘部分并降低泥石流前端部分的抗剪切力，而不能降低中间和后部的抗剪切力。除了滑水假说，另外一个权威性高的假说是动态孔隙压力波动(Dynamic Pore-Pressure Fluctuation)假说(Iverson et al.，1989)。在忽略泥石流本身的强度和黏滞性的情况下，该假说中认为动态孔隙压力波动具有降低摩擦力的作用，从而导致低阻力运动现象。然而，在论证该假说的实验中并没有观察到低阻力运动现象。基于旋转水槽的实验结果，Deng et al.(2017)制作了低视摩擦角(约为1°)的水下泥石流，并提出在整个泥石流与海床接触部位(无论海床是否光滑)由于颗粒撞击槽底而产生动水压力，即DAH假说。该假说的主要问题是实验中并没有测量动水压力。

本研究采用旋转水槽和新开发的测量系统，实测水下泥石流底部水压，本项目参照Deng et al.(2017)的旋转水槽实验方法，实验室模拟水下泥石流的低阻运动；通过实测水下泥石流阻力坡降、槽底正应力和液体压力，评估水下泥石流底部水压，为揭示水下泥石流低阻力运动机理提供实验依据，新开发的测量系统的精度达到±1.5ikPa，为低阻力运动泥石流的水压测量开辟新途径。

1 试验方法

水下泥石流制作设备为旋转水槽(图1)(Deng et al.，2017)。试验中的水槽直径29icm，宽度6icm。在两组试验中，分别使用两种粒径的石英砂(密度2.65iton·m-3)，即300目(48iμm)硅砂和20～40目(850～425iμm)硅砂。前者较细，在本文中成为S组硅砂，后者较粗，在本文中称为L组硅砂。两种硅砂的质量均为80ig，水的质量为635ig。在旋转水槽匀速稳定运行时，形成水下泥石流。与野外观测到的水下泥石流类似，旋转水槽产生的泥石流由两种形态的流体组成：悬浮流和密集流(图1b)。与野外观测到的水下泥石流不同的是，旋转水槽的泥石流形态可控：旋转水槽的转速较低时，密集流的体积较大；旋转水槽高速旋转时，水槽内所有的固体颗粒可能全部悬浮在水中，导致密集流消失。此外，旋转水槽的运动状态可控，可以方便地测定不同运动状态下的槽底水压：在旋转水槽运动过程中，槽底可能会产生径向的附加水压；在旋转水槽突然停止运动后，槽底的附加水压逐渐消失。由此可验证以往研究者中关于槽底水压的假说。因此本研究中，旋转水槽有两种运动状态：匀速旋转运动和静止。

图1 旋转水槽试验

在水槽匀速旋转时，悬浮流与密集流之间有近似为直线(圆周附近的割线)的界面(图1c)，该界面的倾角(Deng et al.，2017)，即为密集流的视摩擦角β。β的测定方法与以往研究一样，是通过测定其对应的圆心角θ得到的，测量误差小于1°。在S组硅砂的试验中，当槽底的速度v过小(v≤0.006im·s-1)时，硅砂会大量黏附在槽底；当槽底的速度v过大(v≥0.23im·s-1)时，硅砂会全部悬浮在水中从而无法得到密集流。因此，试验中槽底的速度v的范围设定在0.014im·s-1到0.11im·s-1之间。稳定的水下泥石流形成之后，密集流的视摩擦角β几乎不发生变化，因此密集流相对于槽底的相对速度就是槽底自身的速度v。在本文中的密集流速度v，实际上是密集流相对于槽底的速度v(图1c)。

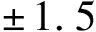
2 试验结果

2.1 视摩擦角β和水压u

在水槽匀速旋转时，两组试验的β如图2所示。两组试验得到的β差异明显：(1)L组的运动不如S组稳定，导致β有较大的波动，同一个速度v对应的β的上下限之间的差异达到10°；S组的运动稳定性较好，除了v=0.11im·s-1情况下有小波动导致对应β的上下限之间的差异达到1.4°之外，测得的其他的β的波动都不到1°。(2)L组的β明显大于S组的β。L组的β平均值的范围是25.6°～31.7°，而S组的β范围是0.7°～22°。两者的差异明显。(3)在速度v较高的情况下，S组的β值非常小。例如v=0.091im·s-1的情况下，β约为1°。这种低β的情况与以往研究结果一致(Deng et al.，2017)。

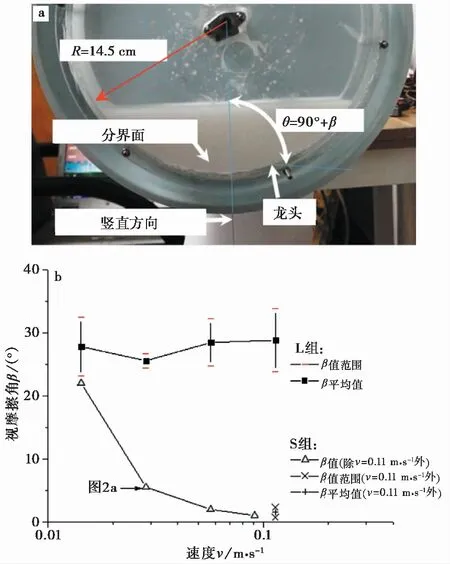
图2 水槽匀速旋转时的实验结果

根据以上结果，有两个现象值得进一步研究，一个是流体运动稳定性的差异现象，另外一个是β低至1°的现象。由于流体运动的稳定性与很多因素相关，本研究不予深入讨论；由于本研究中可以实测水压，且水压可能是影响β的一个重要因素，因此在本研究中实测了水槽匀速旋转和静止状态下的水压，尤其是观测了突然停止旋转之后水压的变化情况。

将水槽突然停止旋转的时刻记为零时刻，图3为有代表性的水压变化历史。对于L组试验，图3a为L组试验典型的水压变化历史：在水槽突然停止旋转后的大约1is之内，水压出现大幅波动；在此之后，水压基本不变。对于S组试验(图3b～图3e)，水压变动情况比较复杂：水压的变动幅度大，且变动情况与测点位置(图3)、停止旋转前的速度v相关。图3b 中的水压变化比较小，原因是测点位于密集流的龙尾之后，测定的水压实际上不是密集流底部的水压，而是悬浮流底部的水压。图3c中的水压变化很大，在经历一个微小的上升之后，水压在120is之内大幅下降了约50iPa。图3e中的水压则是在水槽停止旋转之后在5is之内大幅上升了约50iPa。

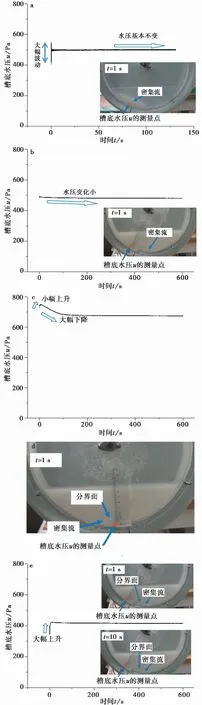
图3 水槽停止转动后槽底水压历史

图3中的t=0时刻是根据侧壁上的水压传感器(图1)的测量结果判断的。如图4所示，由于水槽转速突然降到零，导致槽底水压的测量值有一定的波动，但槽壁水压的测量值相对比较稳定，因此根据侧壁水压的测量结果确定水槽转速为零的开始时刻。

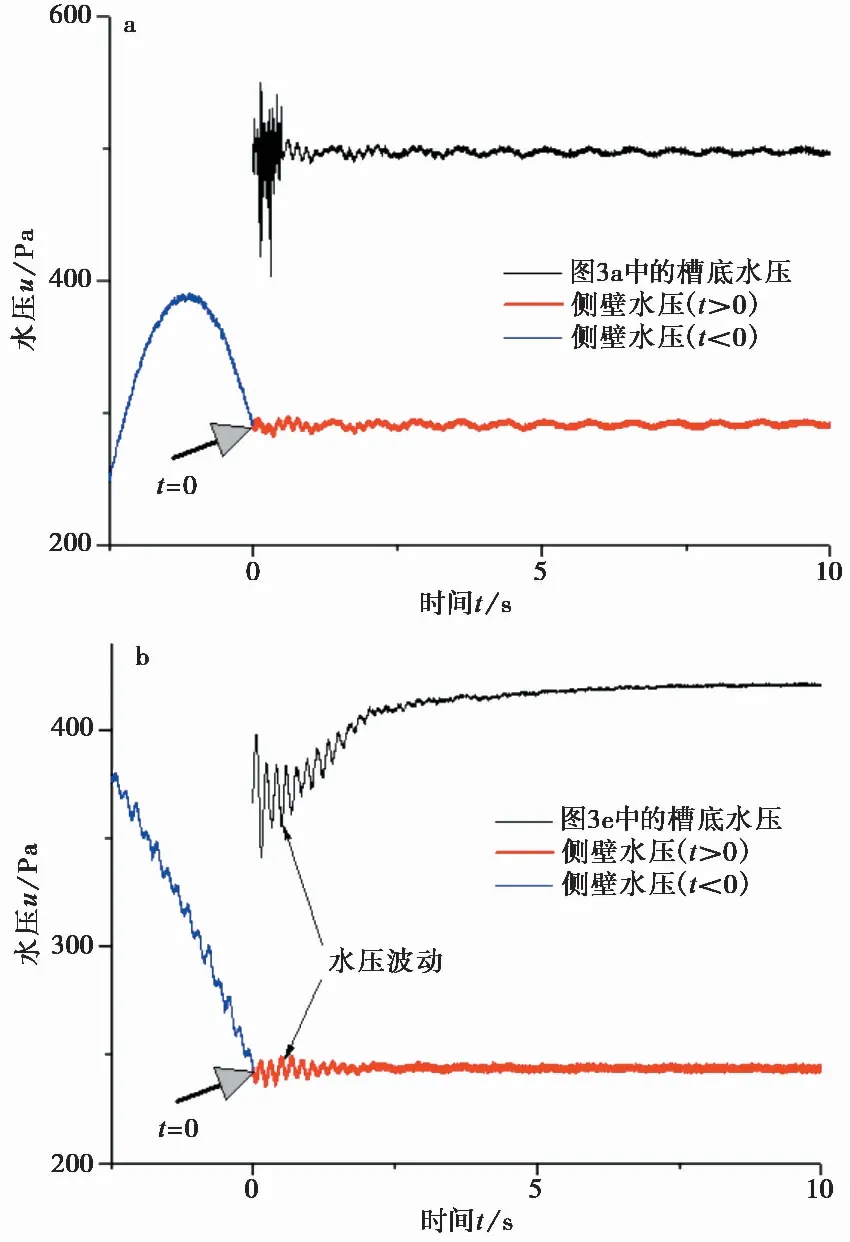
图4 判断转动停止时刻(t=0)

2.2 附加水压Δu

式(1)表示了槽底水压u的组成：

u=ust+Δu

(1)

式中：ust为静水压；Δu为静水压之外的其他水压，即附加水压。试验中，在水槽停止旋转的前后，水体的形状基本不变，因此其对应的静水压ust基本不变，所以在考虑水压变化时不考虑静水压ust的变化。Δu由两部分组成：

Δu=Δusus+Δuden

(2)

式中：Δusus为悬浮流引起的附加水压；Δuden为密集流引起的附加水压。由图3b的试验结果可知，Δusus悬浮流引起的水压变化比较小。Δuden由两部分组成：

Δuden=Δuvol+Δunon-vol

(3)

式中：Δuvol为密集流骨架的体积变化引起的附加水压；Δunon-vol为密集流骨架的体积变化之外的因素引起的附加水压。Δuvol的典型表现是超孔隙水压(Deng et al.，2011)，即剪切时由于土体的剪缩(或剪胀)引起土体骨架的体积减小(或增大)从而引起孔隙水压的上升(或下降)。

根据式(1)～式(3)，可得到如下表达式：

Δu=Δusus+Δuvol+Δunon-vol

(4)

u=ust+Δusus+Δuvol+Δunon-vol

(5)

图3中t=0时刻测定的水压即为式(5)中的水压u；t>0时的水压变化，是因为式(4)中的Δu随时间变化。

式(4)可用来解释图3和图4的试验结果：

图3a和图4a的槽底水压测定结果可以解释为：t=0～1is之间水压大幅波动的主要原因是水槽停止转动后粗颗粒在惯性作用下的碰撞和(或)滑移引起的附加水压Δu；由于粗颗粒的透水性好，这种附加水压只是瞬时存在，因此水槽停止转动1is后水压基本不变。

图3b的水压变化情况可以解释为：由于测点位于密集流的龙尾之后，测定的水压实际上是悬浮流引起的附加水压Δusus，而悬浮流的水压随悬浮颗粒的沉降而不断降低，由于这种水压降低的幅度比较小而且水压降低的速率比较低，因此水槽停止转动后水压变化小。

对于图3c，在水槽停止转动的很短一段时间内，密集流的骨架体积变小引起水压上升，即Δuvol>0，因此出现了一个微弱的水压上升过程；其后，这个新增的水压Δuvol和槽底原有的正的水压Δunon-vol在100is内逐渐消散，因此总的水压在100is内大幅下降。

对于图3e和图4b，槽底原有的Δunon-vol本来是负值；测点上方的密集流在水槽停止转动后的短时间内(大约3is)快速向下移动，导致测点上方原有的密集流消失(图3e中t=10is的照片)，并引起水压的波动(图4b)；因此这个负的水压Δunon-vol很快消散，而总的水压u快速、大幅上升。

为进一步证实槽底的Δu的存在，采用式(6)评估S组试验中不同测点位置、不同v对应的Δu：

Δu=ut=0-ut=10imin

(6)

式中：ut=0和ut=10imin分别为t=0 和t=10imin的水压u。式(6)的根据是：

ut=0=u

(7)

另外，假设式(1)中的附加水压Δu在t=10imin时刻全部消散，因此：

ut=10imin=ust

(8)

根据式(1)、式(7)和式(8)，可得式(6)。

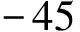
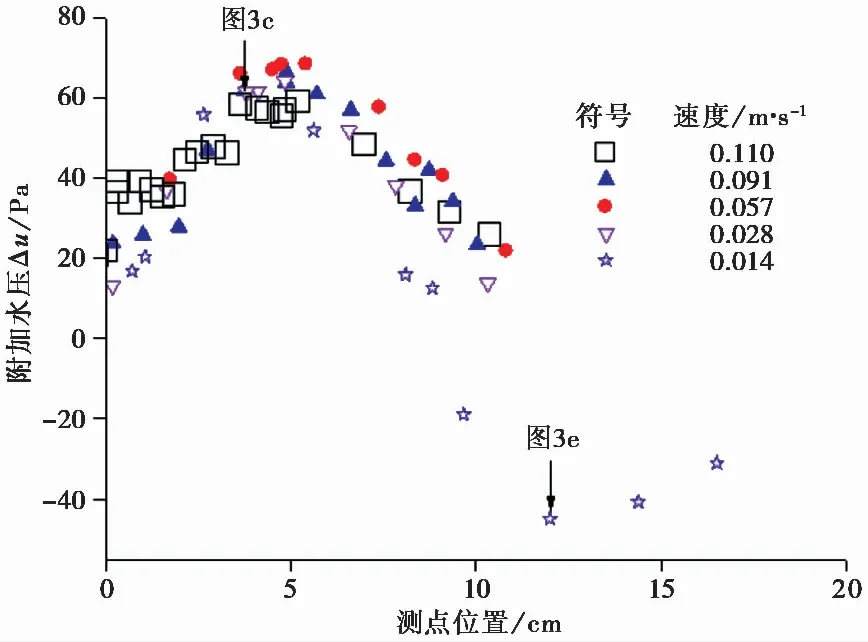
图5 密集流底部的附加水压

需要说明的是，作为式(6)的前提条件式(8)并不严格成立，即附加水压Δu在t=10imin时刻没有完全消散。由于式(4)和式(5)中Δusus与悬浮颗粒的沉降直接相关，而试验中细硅砂的沉降比较缓慢，因此在t=10imin时刻，即使式(4)和式(5)中的Δuvol和Δunon-vol都已经接近完全消散，但Δusus还继续会缓慢降低，只是此时降低的速率很小，因此水压u的测量值还在继续缓慢降低(图3c)。这也说明，根据式(6)得到的图5中的附加水压Δu低于真实的附加水压。

2.3 试验研究的特点与局限性

目前该试验方法在试验方法、试验装置、试验本身等方面还有多个问题需要解决。在试验方法方面，影像法确定密集流与悬浮流的分界面具有局限性：图3中的分界面比较模糊，导致β角的确定存在1°的误差，因此即使β角的测量值已经非常接近0°，仍然只能β角为1°以下而不能说近似0°。在试验装置方面，制造误差和组装误差导致装置有轻微的振动，这种振动可能对β角有一定影响。此外，试验本身只是模拟β角，而没有得到水下泥石流的形成和演变机理，因此本试验不能代替传统的水槽试验。

3 水下泥石流低阻力运动机理讨论

试验结果证明(图5)，在水下泥石流的底部可以产生附加水压，这个附加水压可能与水下泥石流的低阻力运动密切相关。图2中，在v>0.014im·s-1的情况下，S组所有的β都小于5°；图5中，在v>0.014im·s-1的情况下，都观测到了明显的正的附加水压Δu，这说明正的附加水压与密集流(即水下泥石流)低阻力运动密切相关。反之，如果附加水压近似为零(图3a所示的L组试验结果)或者出现幅值较大的负的附加水压(图5所示v=0.014im·s-1情况)，那么β都会比较大(大于22°)，说明附加水压接近为零或负值不利于形成水下泥石流的低阻力运动。两方面的试验结果都证实了附加水压与水下泥石流低阻力运动之间的相关性。

对于在槽底产生正的或负的附加水压的机制，尚需进一步研究。附加水压形成的机制或许与颗粒碰撞槽底(DAH)有关，例如图4a中粗颗粒在水槽停止转动之后粗颗粒在惯性作用下的碰撞和(或)滑移引起了水压的起伏变化，即产生正的和负的附加水压。在透水性比较差(例如S组细硅砂)的前提下，如果正的附加水压效应大于负的附加水压效应，那么在槽底就会测到正的附加水压(图5中Δu>0的数据)，反之，就是负的附加水压(图5中Δu<0的数据)。然而，以上关于附加水压机制的讨论缺乏详实的试验证据，还需要更多的试验揭示附加水压的产生机制。

4 结 论

以往的旋转水槽试验中观测到了稳定运动状态下具有非常小的视摩擦角β(例如1°)，即水下泥石流低阻力运动现象。在本研究中，通过使用一种改进的设备，再现了水下泥石流低阻力运动现象，并测定了水下泥石流底部的水压。结论如下：

(2)该附加水压与水下泥石流低阻力运动具有强烈的相关性。正的附加水压有利于形成密集流(即水下泥石流)的低阻力运动，形成较小的视摩擦角β(小于5°)；反之，如果附加水压近似为零或者出现幅值较大的负的附加水压，那么β可能会比较大(大于22°)。由于S组试验密集流的最大厚度不超过12imm，前述69iPa的附加水压Δu对降低水下泥石流的运动阻力具有重要的作用。

(3)在密集流底部由密集流自身引起的附加水压Δuden由两部分组成：密集流骨架的体积变化引起的附加水压(Δuvol)和体积变化之外的因素引起的附加水压(Δunon-vol); 后者可为正也可为负。Δunon-vol的形成机制可能与颗粒对槽底的撞击有关，但具体的形成过程目前还不明了。