安装误差对单轴旋转对准精度影响分析

刘 鑫，贾继超，黎 坤，赵瑞星，董树冰

(1．航天科技集团 九院16所，陕西 西安 710100；2．火箭军装备部 驻西安地区第三军事代表室，陕西 西安 710100)

0 引言

初始对准技术是惯性导航系统的关键技术之一，初始对准的精度直接决定着系统的精度。单位置初始对准时，水平对准精度与水平加速度等效零位有关，方位对准精度与陀螺等效零偏有关。采用单轴旋转多位置对准可以消除或减小惯性器件的常值漂移对对准精度的影响，从而提高惯性导航系统对准精度。文献[1-4]通过研究惯性器件误差与惯性测量单元(IMU)角位置之间的关系，定量分析了IMU的转动方式，明确了使捷联惯导系统(SINS)误差状态达到最优估计时IMU的最佳旋转角位置。文献[5]系统地分析了多位置对准时卡尔曼滤波器参数(P0、Q、R)的选取对陀螺零偏和加速度计零位的影响规律。文献[6]研究了惯性仪表的随机噪声不同时单轴旋转双位置对准问题。由于单轴旋转多位置对准增加了旋转过程，对准误差源也会发生相应变化[7-9]。文献[8]分析了影响旋转对准精度的惯性器件误差参数，指出天向陀螺标度因数非对称性误差、天向陀螺标度因数误差对航向角对准精度的影响较大。文献[9]指出，采用双位置标定3个陀螺漂移和3个加速度计零位时，陀螺安装偏角会造成水平加速度计零位估计误差。本文将从理论上推导陀螺安装误差对单轴旋转多位置对准精度和加速度计零位估计的影响，并通过单轴旋转多位置对准仿真进行了实验验证，进而为高精度单轴旋转多位置对准方案设计提供参考。

1 单轴旋转多位置对准误差模型

单轴旋转惯导系统的误差传播特性由系统的误差模型来描述。将激光陀螺的零偏和加速度计的零位误差看作随机常值并扩充为状态变量，采用东、北、天(E、N、U)坐标系建立的十阶SINS误差状态模型为

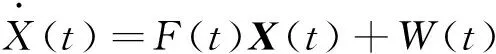
(1)

选择水平速度误差作为量测量，量测方程为

Z=HX(t)+V

(2)

2 陀螺安装误差对对准影响分析

为了确保激光陀螺单轴旋转惯导系统的初始对准和导航精度，必须对误差参数进行精确标定，并通过系统软件加以补偿。而在实际使用过程中，由于惯性器件的性能保持期较短，误差参数会随时间、环境等因素发生改变。为消除或减小了惯性器件的常值漂移对对准精度的影响，可以采用单轴旋转多位置对准方案，而在多位置对准的旋转过程中，陀螺安装误差与旋转角速度的共同作用会造成失准角误差，进而会影响对准精度和加速度计零位估计值。对于激光陀螺单轴旋转惯导系统而言，由于激光陀螺标度因数稳定，由陀螺标度因数误差引起的失准角误差较小，可忽略。

激光陀螺单轴旋转惯导系统常采用转停结合的方式，旋转过程中由陀螺安装误差引起失准角变化率为

(3)

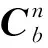
绕方位轴旋转时有ωz≫ωx、ωz≫ωy，且初始对准时接近水平，在旋转过程中由陀螺安装误差引起失准角变化为

(4)

式中ψ为航向角。

最优双位置对准方案是绕方位轴旋转180°，假设初始时刻姿态矩阵为单位矩阵，结合水平初始对准模型，可推得：

(5)

式中g为重力加速度。

由式(5)可知，东、北向失准角估计误差分别为-Eyz和Exz，X加速度计零位估计误差为-Exzg，Y加速度计零位估计误差为-Eyzg。为了提高单轴旋转多位置对准精度和加速计零位估计精度，需要精确标定陀螺安装误差，主要是安装误差Exz、Eyz，Exz、Eyz的标定可以利用单轴速率转台实现。

3 仿真结果与分析

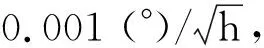
图1、2分别为水平失准角估计曲线和水平加速度计零位估计曲线。由图1可看出，东向失准角估计误差约为-8″，北向失准角估计误差约为4″，与理论分析一致，由图2可看出，X加速度计零位估计误差约为-2×10-5g，Y加速度计零位估计误差约为-4×10-5g，与理论分析一致。

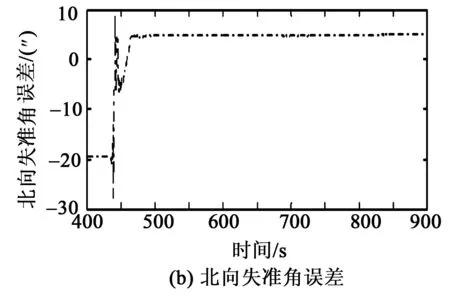
图1 水平失准角估计曲线(局部放大)

图2 水平加速度计零位估计曲线

4 结束语

理论推导了陀螺安装误差对激光陀螺单轴旋转惯导系统对准精度和加速度计零位的影响，并通过仿真进行了验证。从理论分析和仿真验证可看出，陀螺安装误差Exz、Eyz一方面影响水平姿态对准精度，另一方面影响水平加速度计零位估计值。为减小陀螺安装误差Exz、Eyz对激光陀螺单轴旋转惯导系统对准精度的影响，提出基于单轴速率转台的Exz、Eyz标定方案。相关研究为提高激光陀螺单轴旋转惯导系统对准精度提供了理论依据。