基于混沌蚁群优化小波阈值法地磁信号噪声压制

刘 军， 陈 磊， 李文灿， 孟宪武， 刘郁聪， 刘迪仁， 徐学恭， 方江雄， 杨 凤

(1.东华理工大学核技术应用教育部工程研究中心， 南昌 330013； 2.东华理工大学地球物理与测控技术学院， 南昌 330013；3.龙岩烟草工业有限责任公司， 龙岩 364000； 4.北京市京核鑫隆科技有限责任公司， 北京 100101； 5.天津市地震局， 天津 300201)

通过对地球磁场的测量，可用于探明矿产资源分布、分析地质结构和预测地震等。但地磁场是一个微弱的矢量场，由多个磁场叠加构成，且随时间缓慢变化，同时地磁台站的观测环境易受到附近电气化基础设施和实际运行的影响(如铁磁性干扰、车辆干扰等高频干扰)，这些易造成地磁观测数据的质量下降。因此地磁勘探方法需要对所采集的地磁信号进行降噪处理。

冯红武等[1]使用FFT处理地磁信号去除信号中的部分噪声，但当噪声频带与有效信号频带相同时，该方法将无法实现噪声去除；Balster等[2]研究了基于图像特征的小波压缩去噪算法；康传利等[3]对噪声进行多尺度分类组合滤波达到平滑去噪的目的；Shailesh等[4]采用了非局部均值经验模态分解技术对心电图信号进行去噪，还存在模态混叠的问题；苏小会等[5]研究了基于改进小波阈值对遥测数据进行噪声压制；Bhadauria等[6]利用曲线变换和总变异量的自适应融合进行医学图像去噪；汪伟明等[7]采用基于小波分析与数学形态学融合算法对地磁信号降噪处理；Hari等[8]基于小波变换和独立分量分析的核磁共振图像去噪混合自适应算法；龙虹毓等[9]研究了蚁群优化小波阈值法提取变电设备的状态信号，但容易陷入局部最优解。

以上方法对地磁信号噪声压制处理存在降噪不彻底、有效信息被滤除、适用性和泛化能力差等缺点。基于以上背景，本文研究一种用于地磁信号降噪的混沌蚁群优化小波软阈值算法，将地磁信号进行小波变换，利用GCV函数选取小波系数滤波阈值，再通过混沌蚁群优化算法获取最优阈值，以达到较好的降噪效果。

1 小波软阈值去噪方法

1.1 算法原理

假设有一含噪信号：

x(t)=s(t)+n(t)

(1)

式(1)中：x(t)为含噪信号;s(t)为真实信号;n(t)为噪声信号。

利用小波分析方法具备的多尺度观测能力，采用小波软阈值方法去噪[10]，步骤如下：

(1)合理选取小波基和信号分解层数，对含噪信号进行小波分解，得到含噪信号在各个尺度上的小波系数。

(2)选择软阈值函数[式(2)]，对各分解尺度的高频小波系数进行阈值化处理，保留有效信号的小波系数，滤除噪声信号的小波系数。

(2)

(3)对阈值化处理后的小波系数进行小波逆变换，重构获得去噪后的信号。

1.2 阈值函数

阈值λ的确定是阈值化处理的核心。若阈值选取过大，将导致部分噪声无法滤除，去噪效果差；反之，若阈值选取过小，则将带来有效信号被滤除的信号失真。

针对小波阈值去噪算法，常用的小波阈值选取法有Visu shrink阈值、Heursure阈值、Sure shrink阈值和Minmax阈值等。但这些方法皆有一重要前提，需要获取噪声统计特性，但实际待处理数据的噪声是未知的，故噪声统计特性亦无法获得。

GCV阈值函数则避免了需要获取噪声信号统计特征估计的问题，在没有先验信息的情况下，去除噪声的同时仍能保留有效信号[11]。GCV函数表达式如式(3)所示。

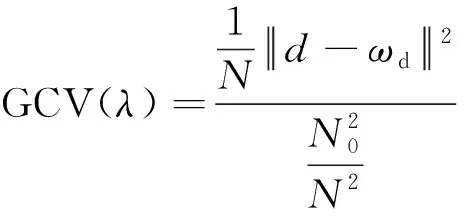
(3)

式(3)中：N为高频小波系数个数；N0为阈值化后被置0的小波系数个数；d为含噪信号的高频小波系数；ωd为阈值化后的小波系数。

从式(3)可以看出GCV(λ)函数的求解只与输入和输出数据有关，无需获取其他信息。

当GCV(λ)函数值最小时，取得最优小波阈值λ，因此将求阈值λ的最优解的问题转化为求GCV(λ)函数最小化问题。

2 混沌蚁群优化小波阈值去噪算法

2.1 Kent混沌搜索算法

蚁群算法是模拟蚂蚁根据信息素浓度搜索食物的行为，具有很强的正反馈特性，但易陷入局部最优解。因此在蚁群优化算法中加入混沌搜索，寻找全局最优解。

针对蚁群算法局部最优解问题，本文结合具有均匀遍历性和随机性的Kent混沌搜索，对蚁群优化的最优蚂蚁个体进行混沌搜索，提高蚁群算法的全局搜索能力[12]。Kent映射为

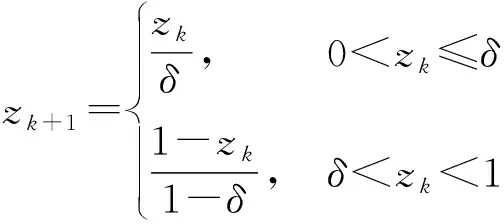
(4)

式(4)中：zk为混沌变量，是区间(0，1)随机生成的数；δ∈(0,1)为控制参数，选择δ=0.4，此时Kent映射概率密度函数在(0，1)内服从均匀分布。

蚁群算法寻优获得最优蚂蚁个体位置后，按式(5)进行混沌搜索，可以得到一个新的蚂蚁位置。对式(5)迭代获得一个混沌序列，将该混沌序列加入原最优解集合作为蚂蚁起点。

(5)

式(5)中：X0、Y0为蚁群优化算法的最优蚂蚁个体位置；Vx、Vy为调节系数；z(j)为混沌变量。

Vx、Vy在迭代前期选取较大系数，加快收敛的速度；而随着迭代次数P变大，搜索范围变小，Vx、Vy也逐渐变小，可找到更精确的解，使算法快速跳出局部最优解。Vx、Vy计算公式为

(6)

式(6)中：|d(j,k)|max为尺度j高频小波系数绝对值的最大值。

2.2 混沌蚁群算法优化算法

混沌蚁群优化算法具有鲁棒性较强，全局搜索性强，算法简单等优点，采用混沌蚁群优化算法对GCV(λ)函数进行寻优[13]，算法中城市为阈值λ，蚂蚁为阈值范围[λmin,λmax]内随机生成的λk，具体步骤如下：

(1)设定初始参数：蚂蚁数为m；最大迭代增加强度系数为Cmax；信息素重要程度参数为α；启发式因子重要程度参数为β；信息素强度为Q；信息素蒸发系数为ρ。

(2)蚁群初始化，将λk赋予m只蚂蚁作为初始位置，初始信息素浓度为τij，混沌搜索迭代次数P。

(7)

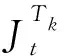
(4)记录本次迭代到访城市和路径，选择最短距离的路径作为最优路径。

(5)考虑信息素蒸发，此次循环在整个路径上的信息素增量，更新信息素，禁忌表清零。

(8)

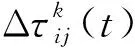
(9)

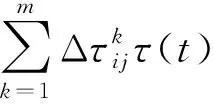
(6)对最优蚂蚁进行Kent混沌搜索后，按照步骤(3)～(5)找到混沌搜索后的最优蚂蚁个体。

(7)判断是否满足终止条件，若满足终止条件，输出最优阈值；若不满足，则回到步骤(3)继续迭代，直到最大迭代次数，输出小波最优阈值。该算法的流程如图1所示。

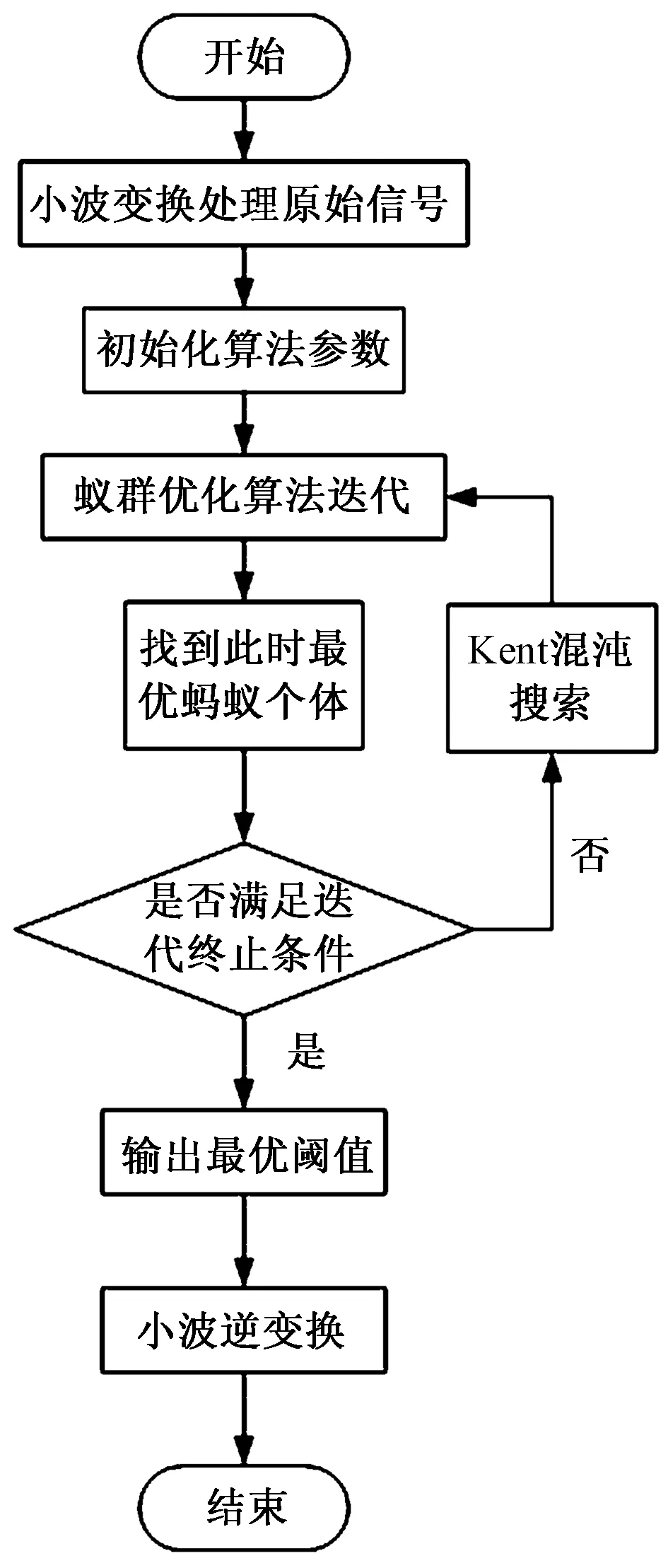
图1 混沌蚁群优化小波阈值算法流程图Fig.1 Flow chart of chaotic ant colony optimization wavelet threshold algorithm

3 实验与分析

3.1 合成正弦含噪信号处理

为验证该算法对地磁信号降噪效果，将不同强度噪声加入一个已知信号中，采用本文算法对其进行降噪处理，计算降噪后信号信噪比(SNR)和均方根误差(RMSE)，分析降噪效果。

先构造1个正弦信号，在正弦信号上加入信噪比为-1、2、5 dB的高斯白噪声作为原始信号。正弦信号如式(10)所示。

y=sin(5x)

(10)

小波分析以双正交小波基函数[如式(11)所示]作为小波基，分解层数为3层。蚁群算法中蚂蚁数量为50，最大迭代次数为200。

(11)

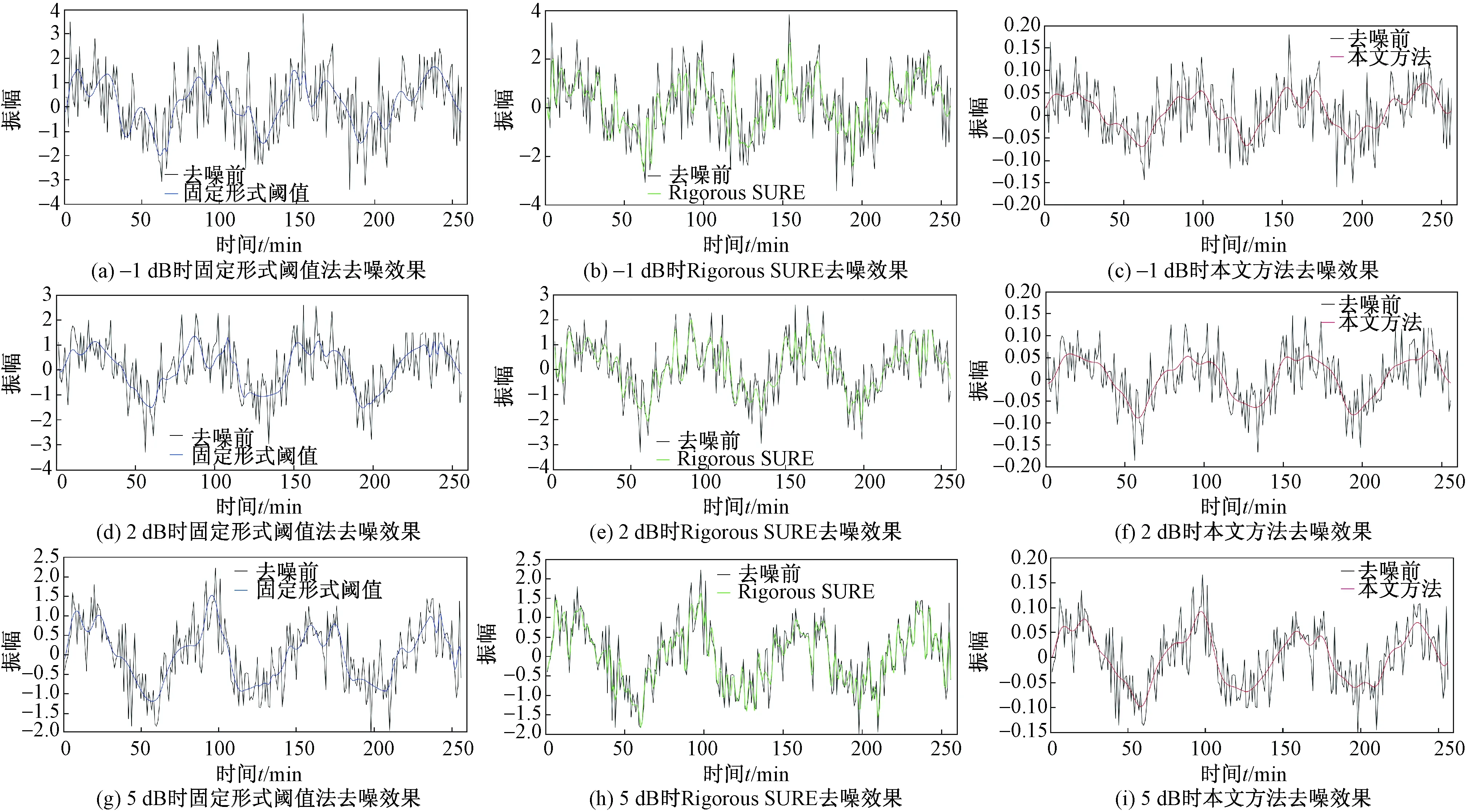
图2 合成正弦信号及各算法降噪效果Fig.2 Synthetic sinusoidal signal and noise reduction effect of each algorithm

选用两种常用阈值法进行去噪对比，阈值选取方法为固定形式阈值和Rigorous Sure(基于Stein无偏似然估计Sure阈值)，阈值选取为软阈值方法。

去噪对比结果如图2所示。其中Rigorous SURE阈值法去噪后信号与原信号相似度较好，但抖动的幅度较大；固定形式阈值去噪信号更为平滑，抖动较小；本文方法去噪信号最贴近真实信号且信号抖动很小，去噪效果最好。

为了更为直观地表达去噪效果，引入信噪比(SNR)和均方根误差(RMSE)作为表征：

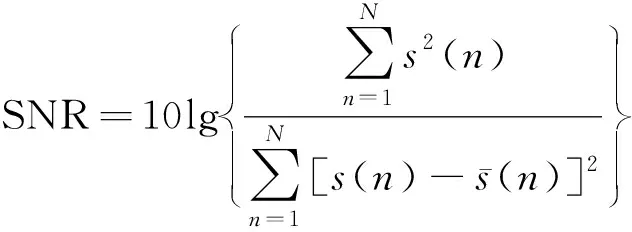
(12)

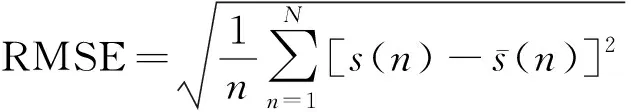
(13)

本文方法与对比方法对含噪的正弦信号处理后的信噪比和均方根误差如表1所示。

由表1中的信噪比和均方根误差可知，针对不同噪声的处理，本文方法的SNR和RMSE都明显优于所对比的两种常用方法，其中RMSE远远小于对比方法。Rigorous SURE方法的SNR和RMSE均优于固定形式阈值；特别地，当信噪比为5 dB时，经固定形式阈值法处理后的信噪比反而降低，说明方法在去噪的同时，还在很大程度上滤除了有效信号。

表1 不同信噪比的正弦信号去噪后信噪比和均方根误差

3.2 实测地磁信号降噪效果

将本文方法应用于实测地磁数据去噪中，实验数据来源为北京时间2018年8月23日在静海地震台实际测量的地磁信号，该信号采样率为1 min，该地磁信号包含大量的噪声，严重影响了地磁资料后续的数据处理。

同样将固定形式阈值和Rigorous SURE方法两种方法作为对比，噪声压制处理结果如图3所示，由图3可以得出：对比算法滤除了部分噪声，去噪波形与原始信号相近，但细节抖动较大；本文算法去噪信号更平滑，抖动较小，去噪效果优于对比算法。

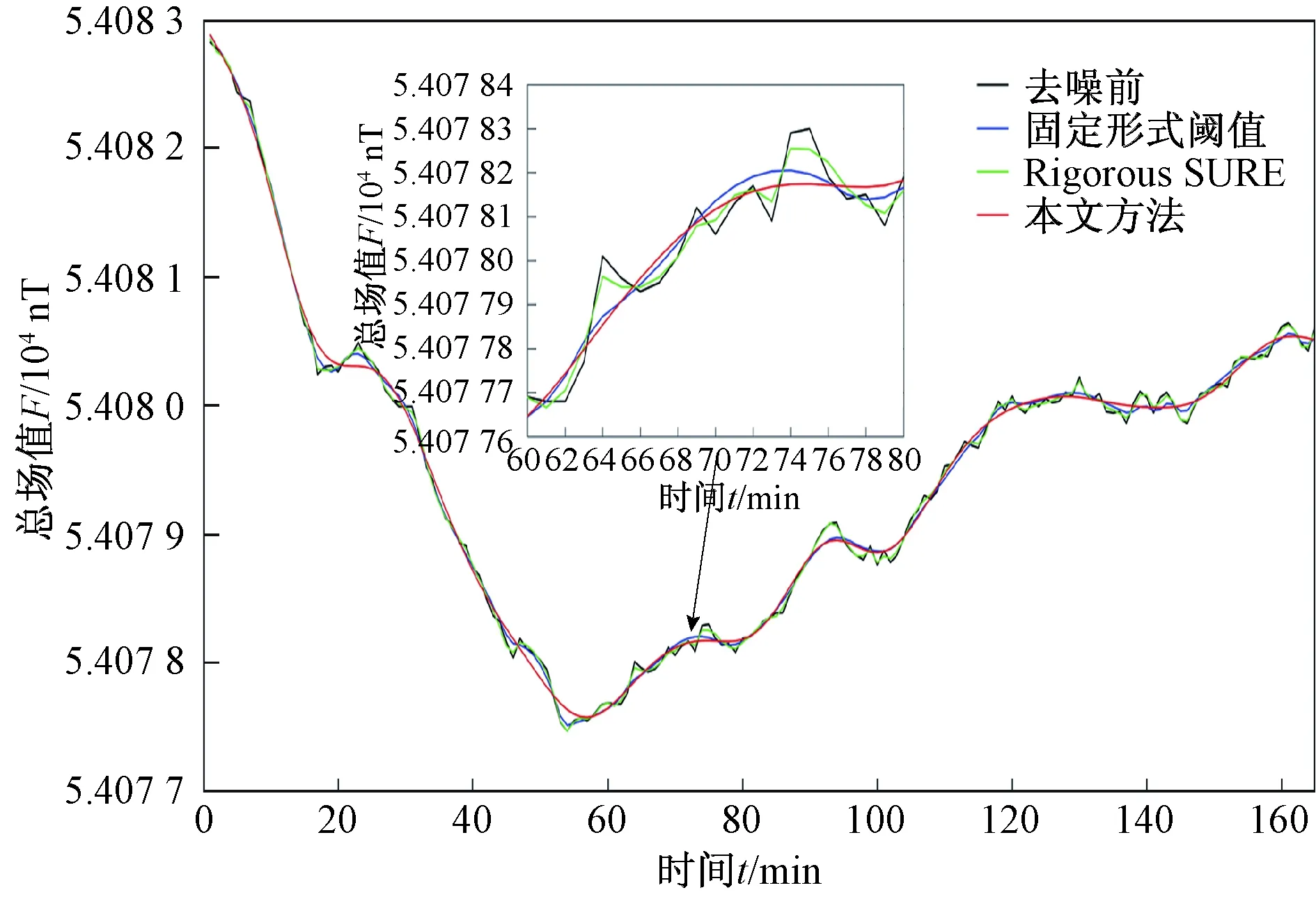
图3 实测地磁信号降噪结果 Fig.3 Measured geomagnetic signal noise reduction results

将实测信号降噪结果60～80 min的局部波形放大，可以更清晰地看出：Rigorous SURE方法去噪信号跟随原始信号上下抖动较大；固定阈值法和本文方法去噪信号更为接近原始信号；但本文方法去噪信号更平滑，抖动最小。

4 结论

针对地磁信号噪声压制处理存在降噪不彻底、有效信息被滤除、适用性和泛化能力差等缺点。研究一种用于地磁信号降噪的混沌蚁群优化小波软阈值算法，利用小波函数对地磁信号进行分解，基于广义交叉验证GCV阈值选取函数，结合混沌蚁群算法对阈值函数进行寻优获取小波的最优阈值。

将本文算法应用于处理实际地磁信号的噪声压制中，通过对比本文方法与常用方法去噪效果，本文方法不仅较大程度地去除了噪声，又较好地保留了信号的有效信息。