有扰下的无线传输监测优化方法

阚保强

(福建师范大学 协和信技系，福建 福州 350003)

无线技术的普及，使得随时随地实现网络接入成为可能，使用者期望无线网络能以更低廉的价格提供更快的传输速率，更多样的业务以及更可靠的服务。然而，无线固有的媒质开放性，各种干扰攻击也广泛存在于无线通信中。如何实现有扰下的可靠通信一直都是无线通信研究者们重点研究的方向[1～3]。要实现干扰下的可靠传输，最直接的方法便是干扰存在时停止传输或通过编码控制降低误码率，无扰时发起传输或提高速率。但要实现这一点，必须对干扰的发起行为有一个准确的估计，也就是通过监测环境来实现，这无疑会带来额外的传输节点的资源开销，对于低功耗无线网络的节点，这种开销往往是不能忽略的，比如无线传感器网络节点[4]。所以如何实现监测开销和传输收益的优化折中显得非常必要。

由于实际干扰的人为控制性，所以其往往是以一定概率分布来实现的。而其分布情况，一般可以根据统计学习的方法获取。所以，在获知干扰满足一定分布的状况下，如何有效地实施干扰监测和传输便是一个非常值得研究的问题。例如干扰源在发起干扰的状态下，如果实施传输显然会造成传输的失败，从而造成资源的浪费。同样，在干扰源处于静默状态的情况下，如果不断地实施监测而不是进行信息传输，也会带来可用资源的浪费。但要实现对监测和传输的高效控制也是困难的，这是因为干扰源攻击行为的随机性，即当前时刻处于静默状态并不能保证在未来时刻依然保持静默。为了实现干扰监测与传输控制的最优化，本文提出了基于部分观察马尔科夫决策过程的问题建模方法，给出了每一阶段最优化决策判决条件。为了便于分析，本文主要考虑外部干扰。

本文安排如下：首先介绍相关研究工作，接下来详细分析了模型和问题形成，然后给出了具体的优化方法，最后给出实际仿真结果。

1 相关工作

无线网络在实现普适计算环境中提供持续的连接服务，从而改善人们的生活质量。但是，由于无线链接的固有空间开放性，当前的无线网络很容易受到各种干扰攻击。所以干扰和抗干扰一直是无线领域的热点问题，相关的抗扰方法，已有大量文献报道[5～7]。

对于如何避免干扰攻击以实现高效传输，传统的研究主要从三个方面入手：1)分析现有类型干扰器，比如有源干扰、灵巧干扰等；2)解析定位干扰源的协议，也就是干扰源发起的攻击层，物理层的易于监测，但是对于上层的协议攻击，则监测往往需要较大的协议开销； 3)干扰对抗策略，即采用物理层空间分集的抗扰技术还是协议层的抗扰策略[1]。在不同类型的攻击中，拒绝服务(DOS)攻击是最普遍且功能最强大的攻击之一。DOS可能会阻止并尝试阻止合法用户获得指定的网络资源[5]。干扰主要是在干扰接收端发射噪声破坏无线网络的传输，即通过注入高电平的噪声来征服要发送的信号，从而降低信噪比(SNR)，从而降低有效数据包接收率。很多学者针对干扰和抗干扰进行了大量研究，比如Achour等人解决了选择性干扰的问题，在这种类型的攻击中，网络中存在的恶意节点会在网络中广播具有重要意义的选择性消息，但通过在物理层进行处理，可以将这些攻击的影响降至最低，但是通信开销较大[3]。Ratnael等人提出了一种称为“神经模糊分离方案”的方法，用于预防和保护WSN形成的卡纸攻击，关键思想是分离对手节点并确保正确的数据传输，可以识别和分类可疑的痕迹，并重新配置网络以对抗干扰，所提出的方法具有较高的吞吐量和具有低延迟的PDR，但具有较高的开销[5]。在文献[4]，我们提出了一种干扰动态测度的抗干扰多路径方法，但是没有对干扰的风险进行量化评估，也没能将多路径问题进行联合优化建模。综上可以看出，在抗干扰技术方面基本上都需要对干扰进行监测或识别，尤其对于智能干扰，这种开销是非常大的，但是以往研究往往没有考虑这些开销，为此本文将通过传输与监测的优化为对象开展研究，实现干扰下的无线传输监测最优。

2 模型与问题形成

图1给出了一个典型的攻击下的无线传输场景，假定攻击设备(可移动)初始位置靠近于节点3 和4，源节点不具有任何攻击相关的信息(包括移动性、位置、攻击功率等)，源节点对于攻击的认知只能通过丢包率测试来推得。由于攻击的移动性和发起的随机性，传输路径的丢包率也是随机的。假定源节点到目标节点的可用路径数为n.如果源节点可以有效监测到干扰方向，即可通过路径切换实现发起有效传输，但是这会带来监测开销，那么如何有效实现监测和传输优化便显得尤为重要。

图1 攻击场景下多路径传输示意图

图1示出了具有3条可能路径的网络。由于攻击时空多变性，要实现有效的传输，必须实现对干扰的高效监测，然后选择最佳的路径进行传输。但是这会带来一定的开销，尤其对于基于协议进行干扰监测的应用场景，监测开销会更大，所以需要在传输和监测取得一个优化折中。

考虑到干扰源是以一定分布选择非干扰(non-jamming)和干扰(jamming)动作，定义两个阶段的时长分别为Xnon、XJ.所以，从长期来看，网络节点的行为可以认为是在每个(Xnon+XJ)循环内选择干扰监测或信息传输动作(这里不具体到实际的传输方式，都归化为传输动作)，即节点的行为集为{a0,a1,…,an}，其中ai是在第i个决策阶段采取的动作，n是在一个循环内的最后一个决策阶段。

对于节点而言，可选择的动作集为{监测，传输}。当采取干扰监测动作(可以采取RSSI、丢包率等)时，其可得到的观测结果有两种，即“干扰静默”和“干扰发起”；当采取传输信息动作时，其也有两种可能的输出结果，即传输成功(比如接收到ACK)和传输失败(没有接收到ACK)。

在完美检测模式(即节点的检测干扰概率为pd=1，误警率为pf=0)和忽略捕获效应的条件下，当输出结果为“干扰发起”或“传输失败”时，则表示干扰存在。所以，只有当检测到干扰不存在时，节点才能发起传输。也就是说，当检测到干扰存在时，需要等到下一循环再进行决策阶段选择。

如图2所示，令t0表示节点检测到干扰源处于静默状态的初始时刻，为了便于分析可以设为0，{t1,t2,…,tn}分别是下一动作决策时刻和上一动作的输出时刻。由于节点对于网络所处状态的概率性，所以对于上述问题，是典型的POMDP问题。

图2 分段行为决策示意图

1)瞬时收益

定义r(j,a)为在状态j下采取动作a时的瞬时收益，定义网络所处的状态{0}表示non-jammed，{1}表示jammed.由于只有在状态j=0时，才进行决策，所以，只需分析状态j=0下的瞬时收益。

a)在状态0下，采取a=1,即处于监测行为，其瞬时收益为：

r(0,1)=prob(nonjammed@(t+Ks))(-C1)+prob(jammed@(t+Ks))(0)

(1)

b)在状态0下，采取a=2,即处于传输行为。其瞬时收益为：

r(0,2)=prob(nonjammed@(t+KT))B+prob(jammed@(t+KT))(B-C2)

(2)

则

(3)

2)信任值更新过程

Λ(t+1)=[λ0(t+1),λ1(t+1)]，由于只在状态{0}时进行决策，所以只需对状态{0}信任值λ0(t)进行更新。

a)选择a=1,即处于监测行为，如果观测值θ=0时，λ0(t+1)=1；如果观测值θ=1时，λ0(t+1)=0.

3)值函数

(4)

由以上公式可知，两个子函数对λ0(t)是线性的，而取值为值函数对两个子函数的上确面的选取，所以值函数对于λ0(t)是凸的。同时，根据子函数对于λ0(t)是线性增的，则当t给定时，值函数对于λ0(t)是增的。由于值函数对于λ0(t)是线性增的，所以存在最优阈值λth，那么当信任值λ0(t)小于λth，此时选择监测最优。但同时可以看出，最优阈值λth是依赖于时间t的。

3 数值分析

为了便于分析，这里通过设置不同的传输收益B来观察λth的变化情况，以及值函数的分布。图3(a)和图4(a)分别给出了在不同收益情况下，各时段的阈值分布图。可以看出，在传输收益增加的情况下，可以降低发起监测的概率。同时图3(b)(c)、图4(b)(c)分别给出了值函数的分布和总收益的分布情况。只要获取最优阈值λth即可实现传输监测的最优控制。

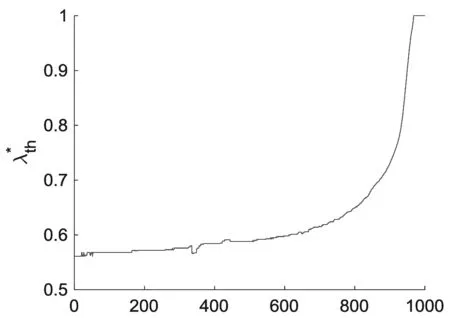
(a)阈值分布

(b)值函数分布

(c)总收益分布

(a)阈值分布

(b)值函数分布

(c)总收益分布

4 结论

本文主要对如何实现干扰监测下的优化传输进行了研究。通过将问题表述为一个部分观测马尔科夫决策问题，给出了每一阶段最优化决策判决条件，得出了最优监测控制下的传输方案。仿真结果表明了本文所提出的方案可以有效提高干扰攻击下的无线网络传输性能。