基于稀疏建模和SVM 的管道缺陷分类方法研究*

郑 林 ，张红星 ，句海洋

(1.太原卫星发射中心，山西 太原 036303；2.中电智能科技有限公司，北京 102209；3.华北计算机系统工程研究所，北京 100083；4.北京工业大学，北京 100124)

0 引言

埋地管道是最有效的油气输送手段之一，对在役管道进行无损检测和安全评价已受到各国的高度重视[1]。 管道在铺设和运行后，由于腐蚀、第三方破坏以及自然灾害等因素的影响，不可避免地会形成一些损伤，需要通过相关的检测方法及时检测缺陷，并评估其对管道安全的影响。 常规管道检测中常用的无损检测（NDT）技术有超声波检测（UT）和漏磁检测（MFL）[2]，属于管道内检测（ILI）范畴，ILI需要克服管道运行压力、流量、变形和管道清洁度对检测精度的影响，而传统的内部检测技术仅适用于已形成的宏观缺陷，对铁磁材料的应力集中和损伤早期诊断无效[3]。 另外，大多数埋地管道都具有限制清管的特点，因此在非开挖状态下，管道缺陷的检测是一个亟待解决的问题。

目前，可用的一些外部检测技术包括涡流（EC）方法[4]、导波检测（GWT）[5]、瞬变电磁法（TEM）[6]和射线扫描法[7]，以上方法称为主动式（有激励信号源）检测，但以上方法均为外部电磁激励检测方法，增加了现场检测的难度，且对于管道损伤等级的划分精度方面存在较大问题。

相关学者从不同的角度对管道缺陷处产生的缺陷磁信号与缺陷参数大小关系进行了实验和研究，针对金属磁记忆检测管道缺陷判定准则的局限性，易方等人[8]构造了五维支持向量机输入特征向量：区域信号的峰峰值、修正傅里叶系数、小波包频带能量增量、信号的检测切向梯度和检测法向梯度。管道状态划分为应力集中、微观缺陷和宏观缺陷3个等级。 张军等[9]选取磁信号的峰峰值和梯度值作为特征向量来描述缺陷信号特征，通过BP 神经网络实现了套管故障风险等级的非线性分类，实验验证了方法的有效性。 邢海燕[10]针对焊缝不同等级的磁记忆特征提取及定量评价难题，引入能够反映焊缝损伤程度的奇异谱熵、功率谱熵和小波空间能谱熵，首次提出信息熵带与D-S 理论联合的磁记忆定量评价模型。 然而，以上文献中所使用的管道缺陷识别方法存在实验样本少、识别模型普适性不足以及无现场实际验证等问题。

鉴于以上问题，为弥补现有埋地管道缺陷损伤程度分类问题的不足， 本文提出基于稀疏建模和SVM 的管道缺陷损伤程度分类模型，采用稀疏模型提取管道缺陷的本质特征向量，并将缺陷特征向量通过改进的多分类支持向量机分类，为埋地钢质管道在非开挖情况的管体损伤缺陷检测提供了一种有效的方法。

1 管道损伤信号特征提取的稀疏模型

1.1 本征模态函数基字典学习

通过实验获取的管道缺陷信号，可以利用VMD算法将其分解为本征模态函数(IMF)，IMF 是不同频率的正弦成分的合成信号，字典D=[d1；d2；…；dN]∈RN×M基元可以设计成具有不同频率、 不同相位、不同延时的信号。

1.1.1 字典初始化方法

聚类分析是数据处理领域常用的方法之一，K-means 是无监督学习的聚类算法，能够很好地处理均衡数据的聚类问题。 为确保字典学习快速收敛，使得不同原子间具备较小的相关度，并且提高字典学习的稀疏建模能力，采用基于K-means 算法对由本征模态函数构成的训练集进行分类。

首先，计算训练样本中所包含的本征模态函数之间的相关度，相关度可以表示为：

学习字典的相关度是指字典中各个原子之间相关度的最大值，可以表示为：

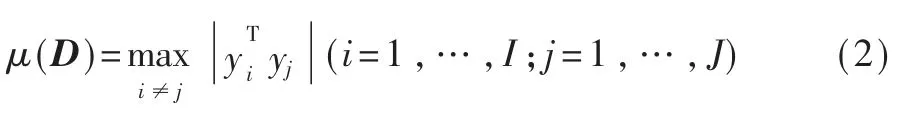
其次，计算每个本征模态函数与其他本征模态函数间的平均相关度。

然后，假设字典的维度为D∈RN×M，将平均相关度最小的M 个本征模态函数看作初始聚类中心。若在这M 个本征模态函数中， 任两个本征模态函数的相关度高于其各自相关度的均值，则将其他本征模态函数中相关度μ¯最小的本征模态函数取代以上两个本征模态函数中¯μ的本征模态函数， 重复以上过程直至收敛。

再次， 将上述得到原子作为初始聚类的中心，做进一步聚类处理，以μ¯作为衡量标准，并采用 K-means 作为聚类算法， 并将最终聚类中心作为初始字典D 中的原子。

最后，字典初始化，实现字典全部更新。

1.1.2 K 奇异值分解的字典更新方法

为防止字典更新时对矩阵的逆运算，本文采用K 奇异值分解（KSVD）算法，该算法与最优方向算法相似，均是根据迭代算法更新字典，均包含字典更新和稀疏编码。 不同之处在于， K 奇异值分解算法对字典进行按列更新时，其对应的稀疏系数同步更细，更有助于算法收敛。 更新每列原子 aj0及其对应的系数，其 中，表示矩阵 X 的第 j 行，求解公式可以表示为：

式中：Y 表示训练集；A 为稀疏模型集合；dj为字典D 中的第 j 个原子；ak为稀疏模型集 A 的第 k 行。

1.2 稀疏模型建立

对于稀疏模型的求解问题可以通过三类方法实现，分别是贪心算法、凸松弛方法以及快速近似法。常用的贪心算法有匹配追踪、正交匹配追踪、弱匹配追踪以及阈值等算法，计算信号和原子之间的内积，从而获取信号的稀疏模型，计算效率高，适用于对计算速度有要求的实际应用问题。

本节所构建的管道缺陷信号稀疏模型是为下一小节处理提供更加简洁的表达，因此，采用基于贪心算法理论的迭代阈值收缩（Iterative Thresholding，IT）算法，该算法可以准确表示管道缺陷信号。 为了高效、快速地处理字典中的信息，采用正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit，ROMP)算法，将D 中的原子的相关系数分为若干组：

在以上分组中，计算分组内的各列向量与其残差的内积，选择绝对值低于最小值二倍以下的数据放入到支撑集中，保证支撑集具备能量最大化的特点。

管道缺陷信号被表示成由VMD 分解得到IMF线性组合，所得到的模态信号近似正交，不可以直接通过分解后的信号获得稀疏模型。 在本小节借鉴层级稀疏建模理论，提出管道缺陷信号层次稀疏建模方法，在层次稀疏建模中，对可以表示成分量信号线性组合形式的混合信号，每个分量信号都有其对应的字典，故可以分别对分量信号进行稀疏建模，进而由分量信号的子字典组成混合信号的字典，可以有效且准确地对信号进行稀疏处理。

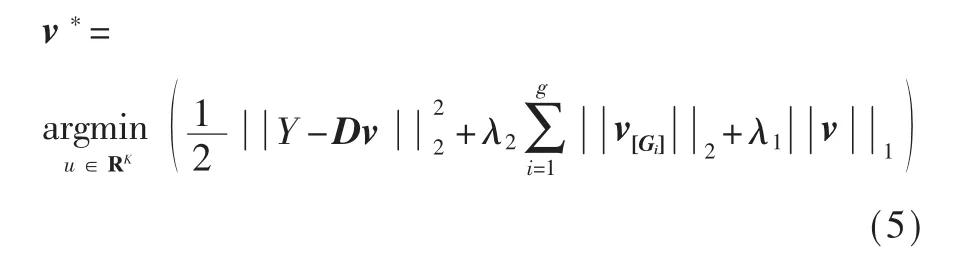
在1.1 节中，已经完成了本征模态函数基字典的构建，可以得到表征原始数据特征的各个模态分量信号，因此，在管道缺陷信号的稀疏建模中，只需对其稀疏度加以约束条件即可，可将正则项省略掉，得到比采用基于层级稀疏建模理论复杂度更低的模型。 在本节提出基于本征模态函数基字典（IMFBD）的管道缺陷信号建模方法中，利用基于正则化正交匹配追踪对管道信号建模，可以确保稀疏建模的准确度以及计算效率。

根据实际管道信号特征，本文构建一个仿真信号如下：

为了验证所建立稀疏模型的性能，对公式(6)中仿真信号进行稀疏建模处理，图1(b)表示稀疏建模过程中的一个原子，重构后信号均方根误差为0.130、标准差为0.129、相关系数为0.993、互信息为4.27，图1(d)是重构信号与原始信号的对比分析。

正交匹配追踪在稀疏建模是基于贪婪算法理论， 将寻优问题转换为搜索和字典 D中原子最大内积问题，通过迭代方式求得全局最优解。 具体实现途径是，选择一个与信号y 最为匹配的原子，构建一个稀疏逼近，并求出其残差，选择与残差最为相关的原子放入到支撑集中，然后对集合中的原子做施密特变换，进而将信号y 映射到更新后的字典中，获取信号y 在集合中的分量，在信号y中减掉该分量，从而得到残差信号，重复以上过程继续分解残差信号，直至达到预设条件终止。

1.3 基于压缩感知理论的信号特征提取方法

压缩感知技术是一种重要的信号处理方法，其改变了信号的传统处理方式， 在将信号稀疏建模后，通过压缩感知方法处理实现了信号的采样和压缩同步，对于管道缺陷信号的压缩感知可以分为稀疏建模、压缩处理以及信号重构。 通过压缩处理将稀疏后的信号映射到相应的矩阵中，所得到的矩阵即为测量矩阵，测量值可以表示为：

图1 仿真信号稀疏建模

式 中 ，Ω ∈RT×N为测量矩阵，T表示测量次数，N是信号长度。

基于IMFBD 对测量信号稀疏建模表示如下：

对于企业来说，安全生产事关经济效益和生产效率的提高，事关企业的可持续、健康发展。对于员工来说，安全事关生命，也是企业对员工的基本承诺。而对于海外项目而言，安全已经成为队伍能否进入国际服务市场首先必须跨越的一道门槛；没有高标准的安全管理体系和良好的业绩就很难通过招投标资格预审，更别说拿到项目合同。

通过公式（7）和（8）可以将测量值（也被称为感知特征系数）表示为：

本征模态函数基字典的稀疏表达磁异常信号特征提取模型流程如图2 所示，首先，对 IMF 进行字典学习；然后，建立基于IMFBD 的磁异常信号稀疏模型，并给出IMFBD 字典学习方法，包括字典初始化、基于迭代阈值收缩（IT）算法的稀疏建模以及基于 K 奇异值分解（KSVD）的字典更新；在此基础上，借鉴层级稀疏建模的思想，提出基于层次稀疏建模思想的磁异常信号稀疏建模方法。

稀疏模型由其基函数确定，基函数确定后，对感知矩阵进行测量，进而得出其测量值。 在信号重构过程中，测量值的每一个元素同等重要，因此，其中的一个或几个元素缺失依然可以对管道缺陷信号重构，解决特征信号的分类识别问题。

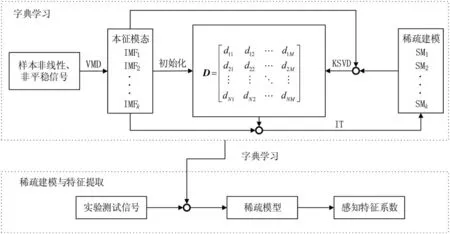
图2 基于本征模态函数基字典的稀疏模型信号特征提取过程

2 基于支持向量机的管体损伤的等级划分

2.1 多分类支持向量机的构造

本文所构建的多分类支持向量机选用的核函数由多项式核函数和RBF 核函数构成，该模型具有更强的学习能力和泛化能力，对于样本数据的分类能力更加准确。 通过将不同的核函数组合学习，可以使多分类SVM 达到适时选取恰当核函数的目的， 实现输入样本数据集到核函数维度的准确映射，并提高SVM 在管体损伤缺陷识别与分类中的精度。

为了使支持向量机具备局部最优和全局最优的性能，引入权重因子η，使其在不同情况合理选择核函数，通过输入的训练样本数据确定合理的权重因子，从而构建多分类SVM，表示形式如下：

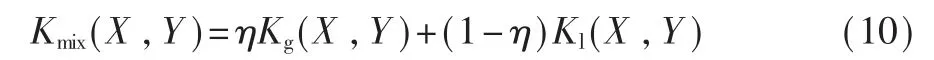
式中，Kmix(X，Y)为多分类 SVM 的核函数；Kg(X，Y)为全局核函数；Kl(X，Y)为局部核函数；η 为权重因子，0＜η＜1。

2.2 基于GAPSO-SVM 算法的管道缺陷分类模型

SVM 的参数选择对其分类准确度和学习速度有重要影响，不合理的参数将导致SVM 陷入局部最优或无法得到预期结果。 由于SVM 算法自身不足性，一些学者研究采用相关的优化算法来对其进行改造。 目前，比较常用的有遗传算法和粒子群算法等，本文结合以上两种算法，构建 GAPSO 优化模型，取其各自优点组成新的混合智能算法。

GAPSO 算法终止的原则：(1)达到优化迭代次数；(2)适应度函数的容差值连续60 次小于其预设值，即全局最优解。 初始参数设置中惯性权重参数的选择极为关键，惯性参数较大时有较好的全局搜索性能，而局部搜索能力对应着较小的惯性权重，因此，随着优化迭代次数的增加，κ 逐渐减小，确保了在算法初始具备良好的全局寻优能力，在后期具有良好的局部寻优能力。 本文 κ 值采用随迭代次数由 0.9 线性递减到 0.3 的方式 ，即 κi=0.9-0.6i/max.num。 另外，粒子群规模设置为 20，进化代数设置为 200，交叉概率设置为 0.3，变异概率为 0.015；为了平衡随机因素影响，将学习因子设为c1=c2=1.5。 为了对比分析 GA、PSO 以及 GAPSO 的计算效率，图3 采用以上设定参数对同一种群进行了计算。

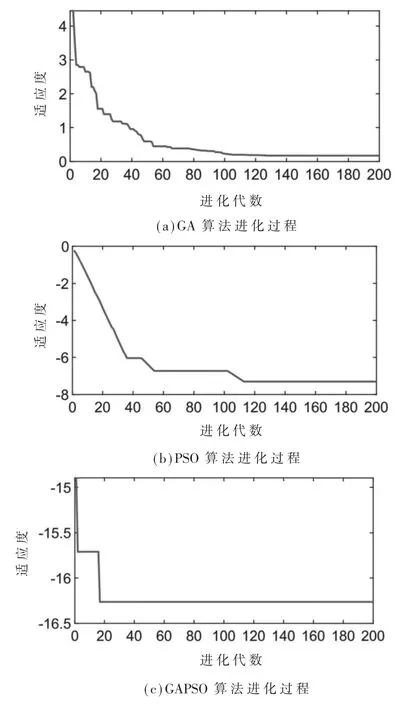
图3 GA、PSO 以及 GAPSO 性能对比分析

在 GAPSO-SVM 模型中，采用 GAPSO 算法来优化惩罚参数 c、权重因子 η 以及核函 σ1和 σ2，并构建初始粒子群向量Y：

为了得到SVM 良好的分类性能，其训练数据集的分类精度 E(yi)的适应度函数 F(yi)为：

式中，F(xi)为第 i 个个体粒子的适应度值；E(yi)为第i 个个体粒子对应的 SVM 的分类精准度。

为了确保种群在合理范围内搜索，将位置和速度固定在预设区间内，即 c 和 g 取值为[0.1，100]。GAPSO-SVM 算法流程如图4 所示。

3 实验数据分析

3.1 检测系统和实验数据采集

图5 所示是所建立的埋地管道缺陷磁异常检测的简化检测模型。

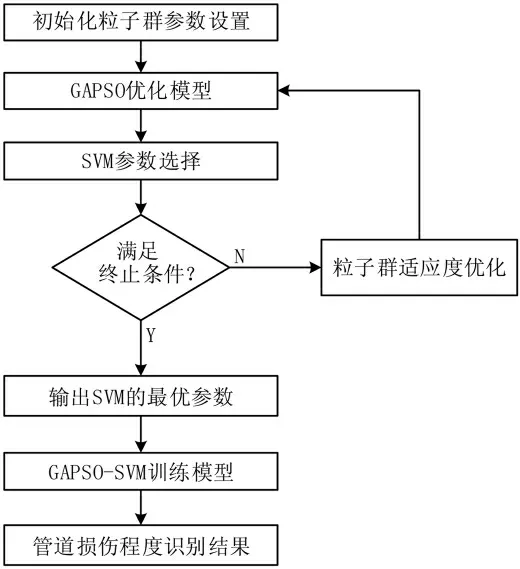
图4 GAPSO-SVM 算法流程

图5 实验检测模型示意图

实验管采用 Q235 钢材料制成，壁厚3 mm，直径75 mm。 为了研究不同缺陷的磁异常信号，在管道的不同位置制作了6 个缺陷，分别是轴向刻槽、横向刻槽、矩形刻槽、通孔、盲孔和 45°刻槽，实验检测时提离距离是管道直径的 5 倍，如图6 所示。

3.2 结果分析

为了获取SVM 的训练样本和验证样本数据集，对实验管道进行缺陷识别试验，并将管道缺陷损伤程度分为三种：低等风险、中等风险以及高等风险，其中，数据集采用3.1 节所描述的管道检测数据。对检测数据进行稀疏建模后，对样本数据与管道缺陷特征进行标记，采用管体缺陷信号的特征向量表示不同的损伤程度，每种损伤等级采集100 组样本，共 300 组样本，其中将每种等级的前 50 组作为训练样本，后 50 组作为测试样本。 根据训练样本缺陷信号与管道缺陷损伤程度对应关系，将归一化梯度能量指数（NGEI）分为三个区间，即[0，0.2]、[0.2，06]以及[0.6,1.0]，分别对应管道缺陷实际损伤程度为低等风险、中等风险以及高等风险，列举部分训练样本（管体缺陷信号的特征向量）见表1。

在选用GAPSO 优化多分类支持向量机的参数之前，首先通过人工随机选取的权重因子η、惩罚参数 c 及核函数 σ1和 σ2的方式构建多分类 SVM模型，其中权重因子 η 取值范围为[0，1]，惩罚参数 c 取值区间为[1，100]， 核函数 σ1和 σ2取值分别为[0.5，100]和[0.1，2]。 通过表2 统计试验结果，可以看出分类识别率最高达到了92.36%， 最低为72.49%。 通过分析得出，随机选取的 SVM 参数难以得到稳定且准确度较高的分类识别率，受人为主观影响因素较大。

在采用基于 GAPSO 算法优化SVM 参数选取过程中，假设权重因子 η 取值为[0,1]，核函数参数 σ1和σ2取范围是[0，10]，惩罚参数 c 的取值为[0，100]，确 定种群数目为 20，最大迭代次数为 200。 为了避免随机误差的出现，利用GAPSO 算法优化 SVM 相关参数的分别计算 10 次，通过 GAPSO 确定惩罚参数值为 30.28、权重因子 η 为 0.4 以及核函数参数σ1为2.63、σ2为 0.96， 采用优化后的参数代入由多项式核函数和高斯径向基核函数组成的SVM 中，构建管道缺陷损伤程度诊断模型，然后对测试样本进行分析。

进一步分析GAPSO-SVM 的性能，将该模型与未进行优化的 SVM、 增量型极限学习机（Increased Extreme Learning Machine，I-ELM） 以 及 BP （Back-Propagation）神经网络算法的处理结果对比分析。 为了避免偶然误差造成的影响，分别将各个模型计算10 次取平均值，计算结果见表3，采用 BP 算法和I-ELM 算法模型的平均精度分别是 79.70% 和82.74%，且不同实验组别的结果波动也较大；采用GAPSO-SVM 模型的准确率可达 93.93%，高于采用未经过参数优化的SVM 模型的结果， 且每次计算结果较为稳定。 因此，GAPSO-SVM 模型在应用于埋地管道缺陷识别和等级划分。

图6 缺陷在在实验管道上的具体位置

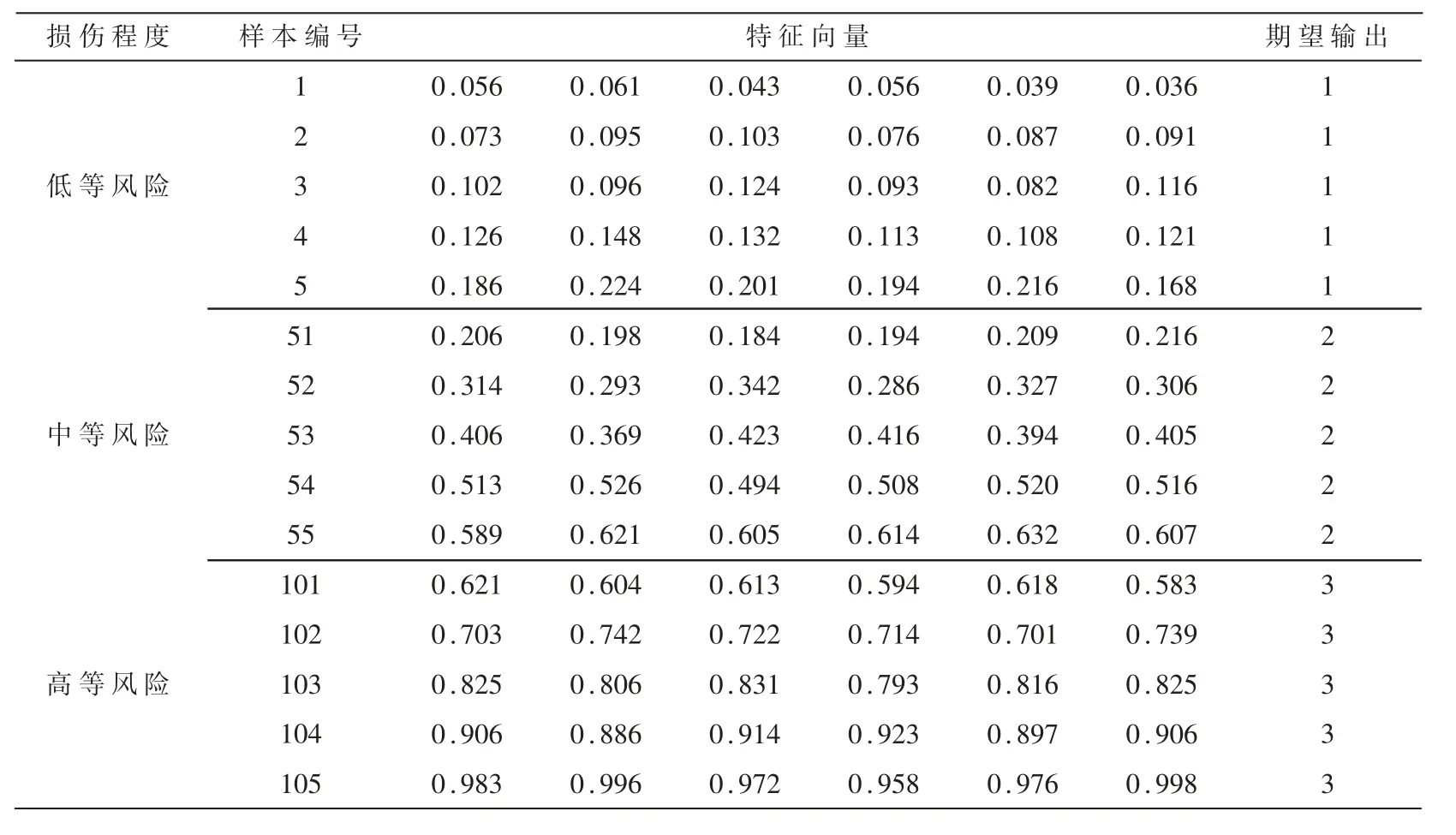
表1 管道缺陷特征信息表

表2 SVM 在不同参数下分类准确度对比

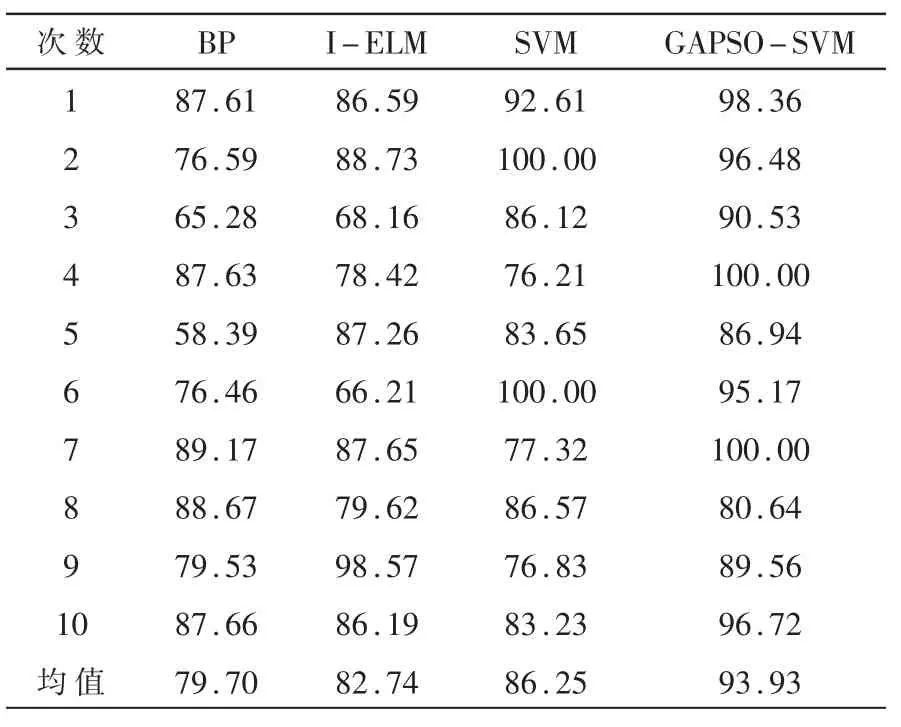
表3 测试集分类准确率（%）分析

3.3 现场检测

2017 年 10 月 30 日，对华北油田某采油厂站内消防管线开展地磁检测现场实验，该管线铺设运营时间已经超过十年，现处于在役状态。

检测结果如图7 所示，管体损伤高风险区2 处，其位置在 21.5 m 和 26.9 m；中等风险区域 3 处，分别在 42.5 m、78.0 m 以及 95.6 m 处；低等风险区域2 处，分别 在 62.0～65.7 m 和 81.2 m 处。 经 过 开 挖验证，符合本次检测分析给出的结论。

4 结束语

本文针对埋地管道非开挖缺陷损伤程度分类问题， 提出了一种基于稀疏建模和SVM 的分类模型。 通过实验数据，对比分析了使用所提出的分类模型和其他模型的缺陷识别能力，并在实际现场中验证了该模型的可行性。 本文得出以下结论：

(1)为了准确提取管道损伤信号的本质特征，本文提出了基于本征模态函数基字典(IMFBD)的管道缺陷信号稀疏建模方法，采用本征模态函数(IMF)进行字典学习，并构建基于 IMFBD 的学习字典。 在以上工作基础之上，通过压缩感知算法，对管道缺陷信号稀疏模型进行分析，提取其特征系数，并通过实验对信号重构即特征提取进行验证分析。

(2)在管道缺陷信号稀疏模型的特征提取结束后，采用基于GAPSO 的多分类支持向量机对管道损伤程度进行分类， 根据GAPSO 算法快速全局优化和支持向量机结构风险最小化的特点，构建基于稀疏建模和SVM 算法的管道缺陷损伤程度评价模型。 通过试验分析表明，本文提出的分类方法具备较高的精准度，且相比其他常用算法在决策稳定性和准确度方面具备一定优势，可以有效解决埋地管道损伤等级划分问题。

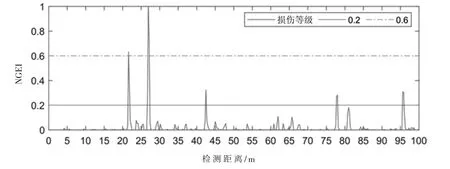
图7 埋地管道管体损伤等级划分

综上，本文提出的管道缺陷分类方法可以在不开挖的情况下直接识别管体缺陷，表明该方法是一种有效的管道本体外检测技术。