基于GWO-SVM 算法的物联网入侵检测研究*

张金霜 ，梁树杰 ，左敬龙

(1.广东茂名幼儿师范专科学校 教育信息技术中心，广东 茂名 525000；2.广东石油化工学院 网络与教育信息技术中心，广东 茂名 525000)

0 引言

随着信息通信产业的发展，物联网技术已被广泛应用于人们生产生活中，其中智能家居就是物联网技术运用的典型代表。然而物联网技术在给人们生活带来便捷的同时，也带来了新的安全威胁，如个人隐私泄露、越权操作、数据破坏等[1]。 其中，物联网的通信与信息安全问题是关键一环，通过使用网络入侵检测技术，能有效抵御或降低此类安全风险。

网络入侵检测的核心是分类算法。 尽管当下使用深度学习进行数据分类十分流行，但支持向量机(Support Vector Machine，SVM)作为一种经典的分类算法，因其具有小样本学习、避免“维数灾难”、算法鲁棒性好等优点，在网络入侵检测的研究中仍占有一席之地，具有良好的推广性和适应性。 在面向物联网环境，相较于其他常见的分类算法，如贝叶斯网络、KNN 算法、模糊聚类、随机森林等，SVM 表现出更好的综合性能[2]。

SVM 的分类效果与其参数选择有较大的关系，关于参数如何选择问题，常用的方法是使用群智能优化算法求解，如粒子群算法(Particle Swarm Optimization，PSO)、遗 传 算 法 (Genetic Algorithm，GA)、人工蜂群算 法(Artificial Bee Colony，ABC)等[3-6]。 针对部分优化算法存在收敛速度慢、容易陷入局部最优解等缺点，本文引入一种新型元启发性优化算法——灰狼优化算法对SVM 参数进行优化。

灰狼优化算法(Grey Wolf Optimizer，GWO)由学者 MIRJALILI S 等在 2014 年提出[7]，它通过模拟自然界灰狼种群等级机制和捕猎行为，确定捕食猎物的位置，实现优化搜索目的。 灰狼算法具有实现步骤简单，需调整的参数少，收敛速度快，有较强的全局搜索能力等特点，在工程领域得到广泛应用[8-10]。

1 理论分析

1.1 支持向量机

分类问题的实质就是基于训练集在特征空间中找到一个划分超平面， 将不同类别的样本分开。而多维的特征空间常常给分类带来困难。 支持向量机在解决小样本、非线性和高维特征空间中表现出独特的优势。 它是建立在统计学习理论的VC 维理论和结构风险最小原理基础上的，通过选取合适的核函数，能有效解决线性及非线性分类问题。

SVM 通过寻找一个最优超平面，使得位于超平面两侧的样本距离该超平面最大，其工作原理如图1所示。

式中，ω 为法向量，决定超平面的方向；b 为位移项，决定超平面与原点之间的距离。

由图1 可知，两个异类支持向量到超平面的距离之和为：

图1 SVM 分类原理图

为了最大化间隔，仅需最小化||ω||2，于是可将式(1)转为凸二次规划优化问题：

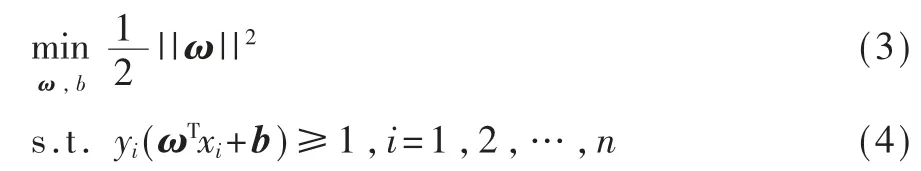
为了防止结果过拟合，提升模型泛化能力，在式(3)中引入惩罚项，目标函数调整为：

式中，ξi为随机数，称为松弛变量。C 为惩罚参数，当C 无穷大时，式(5)迫使所有的样本均满足约束(4)；当C 为有限值时，允许部分样本不满足约束。

进一步引入 Lagrange 乘子，将式(5)、式(6)转为求解对偶问题，引入合适的核函数，可将线性分类问题推广到非线性分类问题。

式中，κ(xi，xj)为核函数，αi为 Lagrange 乘子。 据 此，可得到相应的分类模型：

式中，sgn 是判别函数，用来标注样本的类别(如1 或-1)。

核函数的选择是影响分类模型效果的一个关键，其中高斯核(RBF)使用较为广泛，通过调节核函数半径σ，可实现线性与非线性两种分类器，具有很好的灵活性。 考虑到网络入侵特征向量与入侵行为类型之间存在一定的随机性和非线性，为此本文将采用 RBF 核。

1.2 灰狼优化算法

在灰狼优化算法中，每只灰狼代表种群一个潜在解。算法模拟了灰狼社会等级，分别为 α 狼、β 狼、δ 狼和 ω 狼，依次代表最优解、优解、次优解和候选解。 其中，α、β 和 δ 引导搜索，ω 跟随。

1.2.1 包围猎物

设狼群数量为 N，搜索空间维度为 M，则第 i 头狼的位置定义为 Xi，j=(Xi，1，Xi，2，…，Xi，m)，i=1，2，…，n。 则包围猎物的定义如下：

式中，t为当前迭代次数 ；A和C为系数向量 ；Xp为猎物位置，X 为灰狼位置，D 表示灰狼与猎物的距离。 向量 A 和 C 的计算如下：

其中 a 的分量在迭代过程中从 2 线性减少到 0；r1和 r2是[0，1]中的随机数。

GWO 算法中利用|A |＞1 的随机值来强迫搜索狼远离猎物， 有利于全局搜索；C 为猎物提供随机权重，这有助于在整个优化过程中显示更随机的行为，有利于搜索及避免陷入局部最优。

1.2.2 狩猎

狩猎过程中，α狼、β狼和δ狼拥有更多的猎物信息，因此每次迭代过程中，保留3 个最优解，迫使其他的ω 狼根据这3 个最优解更新自己的搜索位置，具体如下：

式 (16) 得到灰狼个体与 α、β 和 δ 这三狼的距离，式(17)、(18)决定了灰狼个体移动的位置。

1.3 GWO 优化 SVM 参数选择

SVM 的分类效果受惩罚系数 C 与 RBF 核函数半径σ 的影响，仅凭经验值难以保证分类效果，所以优化的目的在于寻找合适的参数。 目前已有研究采用各种群智能优化算法改进SVM 的参数选择。本文在前期研究的基础上，采用 GWO 优化 SVM 算法这两个重要的参数，一方面要提升分类模型的准确率，另一方面要兼顾模型的泛化能力。 最后将分类模型应用于物联网安全入侵检测系统中。 GWOSVM 算法工作过程如图2 所示。

图2 GWO-SVM 算法工作流程图

GWO-SVM 算法的具体步骤如下：

(1)对样本数据做预处理，包括字符特征数值化、规范化等；划分训练数据集与测试数据集，为后续的SVM 模型拟合与验证做准备。

(2)初始灰狼种群规模与迭代次数，将 SVM 的参数 C 和 σ 设定为灰狼个体的位置向量，即 Xi，j=(Ci，1，σi，2)。

(3)计算适应度值，将 SVM 的分类准确率作为适应度值，公式如下：

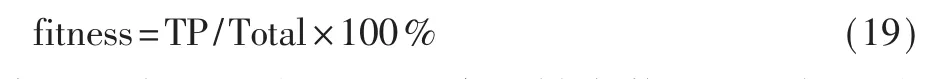
式中，TP 表示所有预测正确的样本数，Total 表示总样本数。

(4)保存最优的前3 个适应度值及灰狼位置。

(5)更新 GWO 中的参数 a、A 和 C。

(6)根据适应度更新ω 狼的位置。

(7)判断算法是否满足结束条件，若满足，则转到(8)；否则转到(3)继续迭代。

(8)获取 SVM 最优参数(C、σ)。

(9)采用最优参数训练分类模型。

(10)运用分类模型对测试样本进行分类。

2 实验分析

2.1 实验环境与数据集

实验采用 Scikit-learn 机器学习库，使用 Python语言编程。

实验采用 UNSW-NB15 数据集[11]，该数据集来自新南威尔士大学网络安全实验室，提供了在综合环境中生成的实际的异常网络流量。 相较于经典的KDD CUP 99，该数据集更贴近当下网络环境，数据内容也更新。 但该数据集的样本区分度差于KDD CUP 99，这给数据分类带来一定的挑战[12]。

为了验证算法的有效性，本文分别与原始SVM、PSO-SVM 和 GA-SVM 在 UNSW-NB15 数据集上进行对比实验。

2.2 数据预处理

由于UNSW-NB15 含有字符型常量，需要进行数值与字符特征值之间的转换，如协议字段，均使用了协议名称或简写，共包含 131 种协议。 按照协议占比排序后再转换为对应的整数，如TCP 协议占比最大，则将其转换为 2，而 UDP 占比次之，将其转换为 3，以此类推。 转换后分别用 2～132 表示。

由于各字段值域不同，有的取值较小，而有的取值特别大，如上下行流量比ttl 字段大很多，不同值域的属性对结果的影响也不一样。 因此，为了平衡各字段对结果的影响，本文采用零均值规范化方法，公式如下：

2.3 模型设置

SVM 的惩罚系数C 值越大，对分错样本的惩罚越大，训练样本的准确率越高，但模型的泛化能力就越低；反之则准确率降低，泛化能力加强。而核函数半径σ 的经验值是 1/n_features。 因此要对 GWO 算法中的狼群位置范围做合理测算。 经多次实验测试，本文将 C 值限定在 [0.1，100]，σ 值限定在[0.001，10]，且尽量均匀分布。

为进一步优化参数选择效果，防止预测结果过拟合，本文在计算适应度值时使用的是综合适应度值，即综合了两组测试结果，分别是训练数据(train_data)预测结果与测试数据(test_data)预测结果，组合比例为 4:6，即 fitness′=fitnesstrain×40%+fitnesstest×60%。

2.4 实验结果

本文实验的训练数据样本为5 000 条， 测试样本为 1 000 条，包含源数据中的各种入侵类型。 标签字段只取“正常”和“非正常”两类，分别用 1 和-1表示。 GWO、PSO 和 GA 初始化种群规模 N=100，迭代次数 t=50。

评价指标采用准确率和 F1 值。 通过实验对测试数据进行分类，其结果如表1 所示。

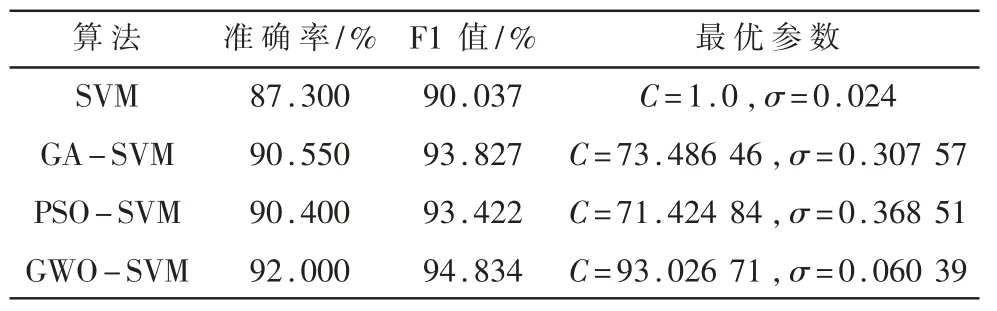
表1 各算法在UNSW-NB15 数据集上的分类结果

由表1 可知，GWO-SVM 算法得到的准确率与F1 值最高，而 PSO-SVM 与 GA-SVM 算法得到的准确率和 F1 值相当，原始 SVM 算法在选用经验值的情况下，准确率与F1 值较低。

由图3 可以看出，GWO 算法与 PSO 算法在第10 代左右都趋于收敛，但PSO 算法未得到最优结果；而GA 算法收敛速度最慢，在28 代左右才趋于收敛，得到的结果与 PSO 算法的相当。 总的来说，GWO 算法比PSO、GA 算法综合表现更好。

综上所述，使用 GWO 优化 SVM 算法具有一定的优势，GWO 算法收敛速度快，寻优效果好，有助于提升SVM 算法的分类效果及建模效率。

3 模型仿真

本研究采用ThingsBoard 框架搭建物联网平台，使用 Raspberry Pi(树莓派)作为终端设备，自行模拟和采集物联网流量数据，包括异常数据和正常数据。采用GWO-SVM 分类算法构建入侵检测模型，并使用平衡二叉决策树方法[13]，实现 SVM 算法入侵检测结果多分类。

图3 适应度值变化曲线图

仿真过程中，共采集 1 000 组测试数据，使用GWO-SVM 模型对测试数据进行多分类，结果如图4所示。

图4 仿真入侵检测结果图

仿真结果表明，使用GWO-SVM 算法得到的分类模型检测准确率高，检测性能良好，适用于物联网环境下的网络入侵检测。

4 结论

本文使用GWO-SVM 算法实现网络入侵检测。GWO 算法在求解最优化问题时有较大的优势，实验中将该算法用于优化SVM 的参数选择，从而提升SVM 的分类准确率。 实验在 UNSW-NB15 数据集基础上，将 GWO-SVM 算法与原始 SVM、PSO-SVM及GA-SVM 算法进行比较，实验结果表明，将 GWO用于优化SVM 网络入侵检测时，在分类准确率与F1 值两项指标上都有所提高，分类效果较好。

最后将模型应用于物联网环境下的仿真实验，并实现了SVM 算法多分类，仿真结果表明GWO-SVM模型适用于物联网环境下的网络入侵检测。