基于DPol-DPMZM的平坦光频梳产生方法①

林 涛，赵尚弘*，曲 光，赵海燕，魏 帅，张 昆，王国栋，李 海，李 赫，李 轩，朱子行

(1.空军工程大学信息与导航学院，西安 710077；2.空军通信士官学校，大连 116600；3.空军研究院系统工程所，北京 100074)

0 引言

光频梳由于其在光任意波形产生[1]、微波光子信号处理[2]、精密光学计量[3]、密集波分复用传输系统[4]等领域的应用而受到广泛关注。近年来产生平坦光频梳的方案有很多[5-14]。例如，在非线性光纤中应用法布里-珀罗光调制器或锁模激光器，然后在超连续介质中产生，可以产生梳齿之间具有固定相位关系的频率梳[5-6]。然而，这些方法都需要一个复杂的方案来保证稳定的运行。例如，采用反馈机制来补偿的环境不稳定性[7]。半导体激光器如基于InP的光频梳发生器可以用来克服这种缺点[8]。不幸的是，尽管这些方法可以得到较大的频率间隔，但是只能获得少量的边带，通常少于10。光纤非线性，如受激布里渊散射(stimulated Bullion scattering，SBS)和四波混合(four wave mixing，FWM)效应也可用于光频梳的生成[9-10]。然而，由于光纤非线性的低功率效率，使得光频梳的平坦度难以保证。基于电光调制器(electro-optic modulator，EOM)的光频梳发生器具有工作稳定、灵活性高、梳状间距可调等优点。基于EOM的光频梳生成方案有很多，如级联强度调制器和相位调制器[11]、级联偏振调制器[12]和级联双平行马赫-曾德尔调制器(dual-parallel Mach-Zehnder Modulator，DPMZM)[13]。然而，这些方法需要具有精确相位差、不同功率和/或不同频率的多通道射频(RF)信号来驱动多个EOMs，这导致了复杂且昂贵的系统结构和较差的可调谐性。为了克服这些缺点，人们提出了只有一个EOM的光频梳产生方案[14-15]。在文献[14]中，使用单个DPMZM生成平坦度为2.73 dB的9线光频梳。然而，由于使用了两个不同频率的射频信号，光频梳的平坦度也受到限制，系统也比较复杂。在文献[15]中，平坦度为1 dB的7线频率梳是通过只使用一个射频信号直接调制单独的DPMZM而不使用任何其他辅助设备产生的。然而，这种方法产生的光频梳的梳齿的数量是有限的。由于缺少其他可调参数来控制幅值和边带数，使得系统难以产生具有更多梳齿的光频梳。相反，DPol-DPMZM调制器有更多的可调参数，可以克服DPMZM的缺点。

在本文中，笔者提出一种新的方案来产生光频梳，该方案只使用一个集成的DPol-DPMZM，使得产生的光频梳具有更多的梳状线和更高的平坦度。根据DPol-DPMZM调制模型推导出的方程，可以从理论上得到梳状数为7、9、11、13的光频梳，并通过实验进行了验证。实验结果表明，生成的光频梳的平坦度分别为1.17 dB、0.96 dB、1.13 dB和2.01 dB, UMSR分别为10.45 dB、10.33 dB、9.54 dB和6.79 dB。此外，还证明了该系统的频率调谐性。

1 系统原理

如图1所示，整个光频梳产生系统主要由一个激光器(laser diode, LD)，一个DPol-DPMZM，两个偏振控制器(polarization controller，PC)，一个检偏器(polarizer，Pol)和一个微波源组成。DPol-DPMZM是一种集成调制器，集成了两个DPMZM，具有体积小，功能灵活的优势。假设激光器的输出信号表达为E(t)=Ecexp(jωct)，由于PC1的作用，使得光载波的偏振方向与DPol-DPMZM中的偏振分束器(polarization beam combiner，PBC)的一个主轴相对准。当光信号进入DPol-DPMZM之后，首先被功分器分成等功率的两路信号。这两路信号分别进入到上下两个DPMZM(DPMZMx和DPMZMy)中。在DPMZMx中，集成了两个sub-MZMs(MZMx1和MZMx2)和一个主调制器。同样地，在DPMZMy中也集成了MZMy1和MZMy2以及一个主调制器。与此同时，RF信号V(t)=Vmsinωmt也被电域的功分器均等地分为两路，在各路上都附带一个功率放大器和一个功率衰减器用于调整注入到DPol-DPMZM的功率，从而达到调整调制系数的目的。两路射频信号分别被用来驱动MZMx1和MZMy1，而另外两个子调制器(MZMx2和MZMy2)没有加射频信号。经过调制，DPMZMx的输出信号可以表示为

(1)

图1 基于DP-QPSK调制器的光频梳产生器的结构图

通过Jacobi-Anger展开，式(1)可写为

(2)

其中，mx是MZMx1的调制系数，定义为mx=πVmx/2Vπ。Vax=πVbiasx1/Vπ，Vbx=πVbiasx2/Vπ，Vcx=πVbiasx3/Vπ表示由DPMZMx中的三个直流偏置电压引入的相移。Vmx表示驱动MZMx1的RF信号幅度。与此同时，DPMZMy的输出信号可表示为

(3)

通过Jacobi-Anger展开，式(3)可写为

(4)

其中，my是MZMy1的调制系数，定义为my=πVmy/2Vπ。Vay=πVbiasy1/Vπ，Vby=πVbiasy2/Vπ，Vcy=πVbiasy3/Vπ表示由DPMZMy中的三个直流偏置电压引入的相移。Vmy表示MZMy1的RF信号幅度。由于y路信号上的90°偏振旋转器，使得x路信号和y路信号出现偏振正交的关系。在PBC的作用下，两个偏振正交的信号耦合在一起，成为一个同时具有两个相互垂直的偏振方向的信号，该信号可表示为

(5)

其中，ex和ey分别为两个相互垂直的偏振方向上的基向量。从PBC输出的信号经过PC2的调整，使得信号中的一个偏振方向与Pol的主轴成45°角。所以，在Pol的作用下，两个偏振方向的信息被同时合并到一个偏振方向上。通过Jacobi-Anger展开，DP-QPSK调制器的输出信号可以被表示为如式(6)所示。

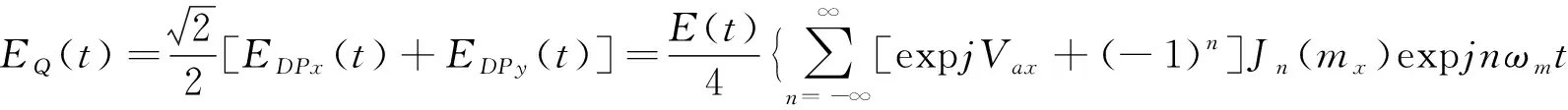
+expjVcx+expj(Vby+Vcy)+expjVcy}

(6)

DP-QPSK调制器的输出信号经过PC2的调整，使得其偏振方向与检偏器的主轴成45°的偏振角。因此，经过检偏器之后，载波信号和各个光边带可以通过式(7)和式(8)表示。

+cos(Vbx+Vcx)+cos(Vby+Vcy)+cosVcx+cosVcy]

(7)

(8)

(1)产生7根光边带

光频梳的一个很重要的特征是各个边带的幅度相等。因此，通过求解等式|EQ1|=|EQ2|=|EQ3|，寻找满足光频梳的参数设置条件。可将该等式通过一个通用的方程组进行表示，如式(9)所示。

(9)

从式(9)可以看出，方程组的解由mx和my两个调制系数确定，因此，可以利用解析几何的方法来寻求解的存在性。将方程组(9)中的所有等式相加起来，得到一个新的表达式如式(10)所示。

Z1=(J3(mx)-J1(mx))cosVax+(J3(my)-

J1(my))cosVay-[J1(mx)+2J2(mx)+

J3(mx)+J1(my)+2J2(my)+J3(my)]

(10)

用解析几何的观点，可以将式(10)的组成看成由自变量cosVax，cosVay和因变量Z1确定的一个空间曲面。假设此空间曲面Z1与另一个空间平面Z2=0有交点，则说明存在mx和my的组合使Z1=0成立，所以解[cosVax，cosVay]T存在。结果如图2所示。

通过Matlab计算，当mx=5.4，my=0.7时，得到[cosVax，cosVay]T的一组解为cosVax=0.8443，cosVay=0.9720。式(7)中的未知参数只剩下Vbx，Vby，Vcx，Vcy四个参数，通过调整这几个参数，满足条件cos(Vbx+Vcx)+cos(Vby+Vcy)+cosVcx+cosVcy= -1.8326，可以很容易的调整载波信号使得其幅度与其他边带相等，即|EQ0|=|EQ1|= |EQ2|= |EQ3|成立从而得到具有7根边带的光频梳。

图2 证明满足具有7根边带的光频梳存在的可能性

(2)产生9根光边带

为了得到具有9根光边带的光频梳，需要满足|EQ1|=|EQ2|=|EQ3|=|EQ4|。与之前的方法相似，建立关于mx，my，Vax和Vay的方程组：

(11)

将式(11)中所有的等式相加，成为一个新的等式，表示为

Z1=(J4(mx)-J1(M1))cosVax+(J4(my)-J1(my))cosVay

-[J1(mx)+2J2(mx)+2J3(mx)+J4(mx)J1(my)+2J2(my)+2J3(my)+J4(my)]

(12)

运用解析几何的思想，将cosVax，cosVay视为自变量，Z1视为因变量，与另一个平面Z2=0组合，选择mx=5.5，my=0.6的条件下，其结果如图3所示。

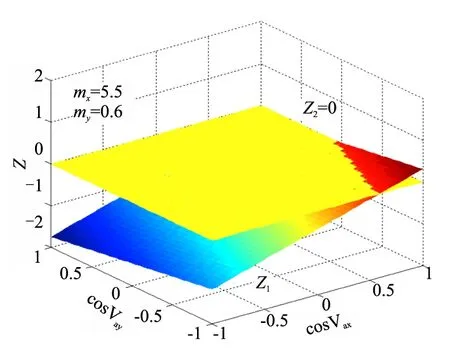
图3 证明满足具有9根边带的光频梳存在的可能性

从图3中可以看出，两个平面存在一系列的交点，因此[cosVax，cosVay]T满足光频梳产生的解存在。通过Matlab进行计算，可以得到其中一组解为cosVax=0.7643，cosVay=-0.2969。与此同时，调整其它参数，满足条件cos(Vbx+Vcx)+cos(Vby+Vcy)+cosVcx+cosVcy=0.2166，从而使得载波的幅度与其他边带相同，使得|EQ0|=|EQ1|=|EQ2|= |EQ3|=|EQ4|成立，继而得到具有9根边带的光频梳。

(3)产生11根光边带

具有11根边带的光频梳需要激发5阶光边带。因此需要提高调制系数，并调整Vax和Vby两个系数满足|EQ1|=|EQ2|=|EQ3|=|EQ4|=|EQ5|。将该关系式写成方程组

(13)

为了便于分析，将所有等式相加，得到新的等式(14)

Z1=(J5(mx)-J1(mx))cosVax+(J5(my)-J1(my))cosVay

-[J1(mx)+2J2(mx)+2J3(mx)+2J4(mx)+J5(mx)]

J1(my)+2J2(my)+2J3(my)+2J4(my)+J5(my)]

(14)

其中，cosVax，cosVay视为自变量，Z1视为因变量，结合Z2=0进行解存在性的研究。选择在mx=6.5，my=0.8的条件下，其结果如图4所示。

从图4中可以看出，两个平面存在交点，说明存在[cosVax，cosVay]T的组合使得|EQ1|=|EQ2|=|EQ3|=|EQ4|=|EQ5|成立，通过Matlab进行计算，得到cosVax=0.3873，cosVay=-0.4174。接着，调整其它参数，满足cos(Vbx+Vcx)+cos(Vby+Vcy)+cosVcx+cosVcy=0.3288，控制载波的功率，满足|EQ0|=|EQ1|=|EQ2|=|EQ3|=|EQ4|=|EQ5|，从而得到具有11根边带的光频梳。

(4)产生13根以上光边带

产生13根光边带，需要产生6阶的边带，并控制这些边带，满足|EQ1|=|EQ2| =|EQ3|=|EQ4|=|EQ5|=|EQ6|。根据该条件，建立方程组

(15)

将该方程组中的所有等式相加，可以得到

Z1=(J6(mx)-J1(mx))cosVax+(J6(my)-J1(my))cosVay

-[J1(mx)+2J2(mx)+2J3(mx)+2J4(mx)+2J5(mx)+J6(mx)]

J1(my)+2J2(my)+2J3(my)+2J4(my)+2J5(my)+J6(my)]

(16)

依照解析几何的知识，将cosVax，cosVay视为Z1的自变量，构成空间曲面，与另一个平面Z2=0相结合，选择在mx=7.3，my=0.2的条件下，其结果如图5所示。

从图5中可以看出，两个平面存在交点，说明存在[cosVax，cosVay]T的组合使得|EQ1|=|EQ2|=|EQ3|=|EQ4|=|EQ5|=|EQ6|成立，通过Matlab进行计算，得到cosVax=0.1889，cosVay=-0.6777。接着，调整其它参数，满足cos(Vbx+Vcx)+cos(Vby+Vcy)+cosVcx+ cosVcy=-1.1955，控制载波的功率，满足|EQ0|=|EQ1|=|EQ2|=|EQ3|=|EQ4|=|EQ5|=|EQ6|，从而得到具有13根边带的光频梳。但是，从分析结果来看，为了产生13根边带的光频梳，调制系数已经达到了7.3左右，接近现有调制器的极限。

从理论上分析，产生15根，17根甚至更多梳线的光频梳都是可行的。分析结果如图6所示，但是由于实验条件中半波电压的限制，无法获得更高的调制系数来满足13根以上梳线的光频梳产生。

2 实验结果

为了验证该光频梳产生器的可行性，搭建了如图7所示的实验系统。波长可调谐激光器Agilent N7714A辐射出的光信号波长为1552.5 nm，功率为13 dBm；DP-QPSK调制器的型号为Fujitsu FTM7977HQA，该调制器的消光比大于20 dB，半波电压大约在3.2 V～3.5 V之间；微波源由Agilent E8257D提供，其最大输出功率为30 dBm；电域的功率放大器使用型号为Agilent 83020A；光谱仪使用YOKOGAWA AQ6370C进行频谱观察。

首先，在DP-QPSK调制器和激光器之间连接一个PC1，通过调整PC1使得光信号的偏振方向与调制器中的PBC一个主轴对准。将微波源的频率设置为7.02 GHz、功率为3 dBm，产生正弦波信号。通过功分器将该微波信号均等地分成两路，经过功率放大器和衰减器之后，各自对MZMx1和MZMy1进行调制，而MZMx2和MZMy2不接任何微波信号。由于整个系统有6个直流偏置点和2个调制系数，总共有8个可调参数，因此很难同时控制产生所需结果，需要根据理论分析，逐步调整参数。首先将两个功率衰减器的衰减系数设为最大，再将功率放大器的功率输出设为最大，通过调整衰减器的衰减系数就能灵活控制调制系数。

(1)产生具有7根光边带的光频梳。第一步，根据之前的理论分析，控制调制系数激发出三阶光边带；第二步，调整Vbiasx1和Vbiasy1控制除载波之外的1到3阶光边带，使得所有的光边带基本处在同一幅度值；第三步，调整Vbiasx2，Vbiasx3，Vbiasy2和Vbiasy3控制载波的幅度，使得其幅度值和其他的边带相同。实验结果如图8(a)所示。从图中可以看出，产生出的光频梳具有7根光边带，0.96 dB的平坦度以及10.33 dB的杂散边带抑制比。

(2)产生具有9根光边带的光频梳。控制调制系数激发四阶光边带，其余的步骤与(1)中的同样，实验结果如图8(b)所示。从图中可以看出，系统产生了具有9根光边带的光频梳，平坦度是1.13 dB，杂散边带抑制比是9.54 dB。

(3)产生具有11根光边带的光频梳。提升调制系数，激发五阶光边带，再调整六个直流偏置点。最后得到的结果如图8(c)所示。从结果中可以得出，该方法能够产生出具有11根光边带，2.01 dB的平坦度，6.79 dB的杂散边带抑制比的光频梳。

(4)产生具有13根光边带的光频梳。如图8(d)所示，继续提升调制系数，激发六阶光边带，通过调整六个直流偏置点，产生的光频梳具有13根光边带，1.17 dB的平坦度和10.45 dB的杂散边带抑制比。

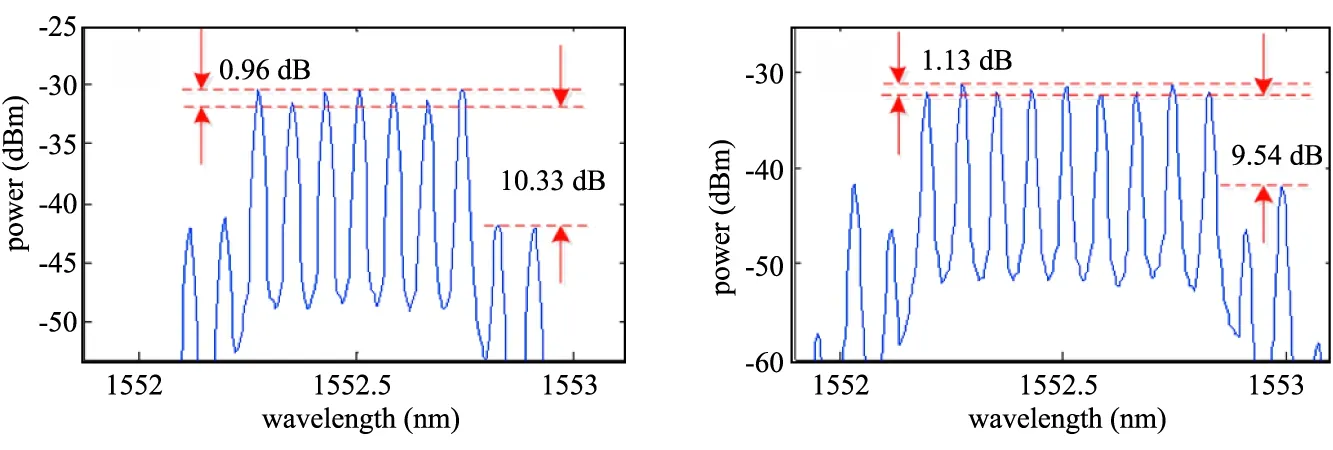
(a) (b)

(c) (d)

为了验证系统的调谐性，将具有9根光边带的光频梳作为研究对象。调制信号的频率分别设为6.02 GHz，7.02 GHz，8.02 GHz和9.02 GHz。其他的参数设置不变，通过光谱仪，可以观察到如图9所示的结果。

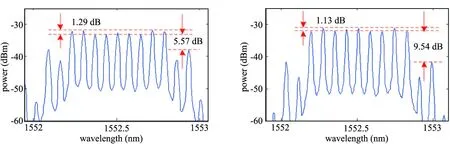
(a) (b)

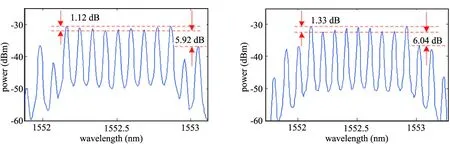
(c) (d)

从图中可以看出，当调制信号的频率设置为6.02 GHz，7.02 GHz，8.02 GHz和9.02 GHz时，其平坦度分别为1.29 dB，1.13 dB，1.12 dB和1.33 dB，平坦度变化仅为0.21 dB；杂散边带抑制比分别为5.57 dB，9.54 dB，5.92 dB和6.04 dB，杂散边带抑制比的变化为3.97 dB。因此，整体的调谐性能较好，能够通过频率在6.02 GHz～9.02 GHz之间的任何调制信号产生平坦度稳定的光频梳。

4 讨论

文中使用的双偏振双平行马赫曾德尔调制器实际上是一种电光调制器，存在直流偏置点漂移的固有问题。对于这种不足，市面上有许多公司已经研制出相应的直流偏置控制回路，可以有效缓解直流偏置点漂移带来的影响。另外，对于调制系数，使用的是安捷伦公司生产的微波源Agilent E8257D，其微波功率的抖动在0.1 dB以内，较为稳定。值得一提的是，整个实验的持续时间在2个小时以上，在这段时间内，光谱仪上显示的光频梳十分稳定。这与调制器本身的质量以及直流电源的稳定性有关。

另外，在整个实验过程中，笔者并未使用过光放大器，因此，最后得到的光频梳功率普遍偏低。要想提高功率，但不升高噪底，有以下几种选择：

1)提高激光器的功率，这种方法比较直接，但是收到了调制器本身的输入功率最大值的限制，因此并不是一个一劳永逸的方法；

2)使用窄线宽的激光器，这样的激光器的RIN很小，相应的噪底就会很低。在这种情况下使用光放大器，噪底的升高对整体光频梳质量的影响不是很大；

3)使用波分复用器来过滤出所需的信号，性能良好的光滤波器在某种程度上是具有降噪功能的[16]。可以首先对光频梳进行功率放大，然后进行光滤波，就可以有效减小噪底的影响。

4)以上三种方法相互结合，这样的效果最佳。

5 结论

本文重点研究了基于单个DP-QPSK调制器的光频梳产生方法。从实验结果来看，通过调整DP-QPSK调制器中的六个直流偏置点和两个调制系数，可以得到边带数分别为7根，9根，11根和13根的光频梳。由于受到调制器半波电压的限制，调制系数无法调得更高，因此无法产生13根以上的边带数。这四种光频梳分别具有0.96 dB，1.13 dB，2.01 dB和1.17 dB的平坦度以及10.33 dB，9.54 dB，6.79 dB和10.45 dB的杂散边带抑制比。除此之外，本章还研究了该系统的调谐性，选取具有9根光边带的光频梳作为研究对象，将频率分别设为6.02 GHz，7.02 GHz，8.02 GHz和9.02 GHz，得到四种不同频率间隔的光频梳，平坦度的变化介于1.12 dB和1.33 dB之间。由此证明了该种光频梳产生技术具有较好的频率调谐性，可满足未来星上多频段通信中的多本振信号产生需求。