基于罗德里格矩阵的水域与陆域点云配准研究

石银涛，董阿忠，赵 钢

(1.南京工业大学 测绘科学与技术学院，江苏 南京 211800； 2.江苏省水利科学研究院，江苏 南京 210017)

近年来，随着RS(Remote Sensing)、LiDAR(Light Detection And Ranging)等测绘新技术和VR(Virtual Reality)、AI(Artificial Intelligence)等计算机科学的融合发展，三维地形可视化与仿真正逐渐成为国内外众多学者研究的热点问题。目前，地形仿真比较常用的是以数字地面模型为基础来拟合地面起伏，结合相应的卫星或航空遥感影像数据给人以更加逼真、直观的场景感受[1]。对于点云建模，常见的是地表建筑物、文物、地形的三维模型重建，而对于水陆地形的点云联合仿真研究则相对较少。同时，随着测绘地理信息科学逐渐由数字化向信息化方向发展，对地理空间数据的要求也正朝着高精度、海量、现势性、可视化的方向发展，空域、陆域、水域地理空间数据的共享和集成化管理对于国民经济建设、社会发展、国家安全以及地球和空间科学研究等各方面都显得愈加重要[2]。由此可见，通过多源数据融合，实现水陆地形的联合仿真具有重要的现实意义，也是今后测绘领域三维建模的趋势之一。

利用多源数据进行地形的仿真，首先必须解决多源数据的配准问题。这是因为不同的数据源所使用的采集设备、参考坐标系、空间分辨率等各有差异，而要综合利用这些数据进行地形仿真，必须要将它们转换到同一坐标参考框架[3]。目前，水下地形数据的获取多采用多波束测深系统进行全覆盖扫测，获取的源数据为水下地形点云(简称“水域点云”)；陆域地形数据的获取多利用地面LiDAR进行采集，获取的源数据为陆域地形点云(简称“陆域点云”)。要实现水域与陆域地形的联合仿真，必须首先要完成水域与陆域点云的配准，即将两类点云转换到同一基准坐标系。目前，从国内外的研究成果来看，根据所选择的配准基元的不同，点云的配准方法大体可以分为无特征配准与基于特征的配准两类[4-5]。无特征配准本质上是基于最小二乘的最优匹配，这类方法对点云的重叠度、初始姿态等要求较高，无法适用于水陆点云的联合配准，因为水陆点云的重叠度通常较低(仅在潮间带有少量的重叠区域)[6-7]。基于特征的配准是指利用物体自身的点、线、面等几何特征或人为添加的标靶等作为同名点解算变换参数，这种方法较无特征配准具有更强的适用性，且能更好地评估配准精度[8-10]。

本文基于三维坐标转换的基本理论，探讨了罗德里格矩阵和间接平差模型在水陆点云配准参数迭代解算中的应用；并以长江南京河段梅子洲的试验为例，分析了该方法在实际工程中应用的可行性与可靠性。

1 水域与陆域点云的采集

目前，水域地形的点云获取主要通过多波束测深系统获取，其采用多组阵和广角发射、接收，从而形成条带式的密集测深数据。与传统的单波束测深技术相比较，多波束测深系统具有测量快速、精确、范围广等优势。它将测深技术从传统的点、线状延伸到面状，并进一步发展到三维立体图，因此使得海底地形测量技术发展到一个更高的水准[11]。多波束测深系统的工作原理是利用发射换能器阵列将宽扇区覆盖的声波发射到海底，利用接收换能器阵列对声波进行窄波束接收，通过发射、接收扇区指向的正交性形成对海底地形的照射脚印，对这些脚印进行恰当的处理，一次探测可以得到与航向垂直的垂面内上百个甚至更多的海底测点的水深值，实现快速连续获取测区范围内水下探测对象的表面特征和起伏变化情况，得到精确的水底地形[12-13]。

陆域点云的获取可以通过地面/移动/空载LiDAR、倾斜摄影测量等手段获取，因而在精细化地形重建中，地面三维激光扫描仪在精度、作业效率等方面具有一定的优势[14]。地面三维激光扫描仪利用激光测距原理，采用非接触式高速激光测量方式，能够自动、连续、快速地以点云形式获取地形及复杂物体三维表面的阵列式几何图形数据。在扫描仪内，扫描控制模块控制和测量每个脉冲激光的角度，针对每一个扫描点可测得测站至扫描点的斜距S，再配合扫描的水平角α和垂直角θ，可以得到每一扫描点与测站的空间相对坐标[15]。一般仪器内部坐标系统为：X轴在横向扫描面内，Y轴在横向扫描面内与X轴垂直，Z轴与横向扫描面垂直。

2 水域与陆域点云的配准

一般情况下，陆域采集的点云多使用独立坐标系，水域采集的点云多使用地方或工程坐标系，要将其联合仿真，两者之间的配准是实现水陆联合仿真的关键。点云配准是一种三维坐标转换，针对欧拉角较小的情况可采用近似处理后的布尔莎七参数模型[16-17]。常规的点云配准中，往往其近似为一种只涉及旋转和平移的刚体变换，而在本文的研究中，由于地面和水下使用不同的仪器设备进行测量，为提高解算精度，考虑了尺度变换的情况。

2.1 三维坐标转换模型

在大地测量的三维坐标转换中，Bursa-Wolf模型、Molodensky模型及武测模型应用的较广泛。针对水陆点云的配准转换，这里采用一种简化转换模型。设有陆域点云P和水域点云Q，其对应坐标系分别为SP和SQ，根据坐标转换的物理过程，则由坐标系SP到坐标系SQ的坐标转换模型为

(1)

式中：R是由α、β、γ3个旋转角所组成的旋转矩阵；T是由3个标量所组成的平移矩阵；λ是尺度因子。有时，将旋转角α、β、γ称为欧拉角，其构建的矩阵R则被称为欧拉角矩阵。

根据式(1)可以看出:三维坐标转换的过程实质上就是解算3个旋转参数α、β、γ构成的旋转矩阵R，3个平移参数构成的平移矩阵T和1个尺度因子的过程。由于转换模型一共含有7个未知量，因此至少需要3对已知同名特征点进行求解。

2.2 罗德里格矩阵的构建

陆域点云与水域点云配准过程中，涉及大旋转角的三维坐标转换，不宜使用简化的布尔莎七参数模型。原因在于，传统的七参数坐标转换以绕坐标轴旋转的3个欧拉角构成旋转矩阵，需要进行大量复杂的三角函数运算和线性化过程，并且参数初值不易确定。本文基于罗德里格矩阵和间接平差模型对点云配准参数进行迭代解算，这种方法只涉及简单的四则运算，在一定程度上提高了解算效率，能够很好地确定参数初始值，通过迭代计算保证了解算成果具有良好的精度。此外，使用间接平差模型能很方便地列出观测方程且方程个数容易确定。

(2)

2.3 参数初值的解算

在采用间接平差模型求解三维坐标转换参数的过程中，参数初值的选取尤为重要,它直接影响着平差系统的稳定性、结果的准确性以及解算效率，且不合理的初值甚至会导致平差结果严重偏离真值[19]。针对参数初值的计算，首先计算尺度因子λ0，再解算旋转矩阵R0，最后计算平移参数T0。

取任意两对同名点i、j在坐标系SQ中的距离和坐标系SP中的距离之比作为尺度参数的初值：

(3)

为提高所求初始值与真值的接近程度，也可取多对同名点，将两两之间组合求出距离比的平均值作为尺度参数的初值。

对于构成旋转矩阵R的3个独立参数a0、b0、c0的确定，在点云P和Q的任意两对同名点i、j所满足的坐标转换模型式(1)间求差，并结合罗德里格矩阵的性质可得：

(4)

(5)

式(5)只有两个独立方程，所以至少还需要1对同名点k，联合i、j两点组成如下方程：

(6)

式(6)为超定方程组，利用间接平差可解出3个独立参数初值的最小二乘解a0、b0、c0，为提高精确度，还可联合多个同名点，两两组合得到多个形如式(5)的方程组进行求解。

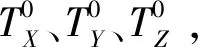
2.4 平差模型的解算

(7)

对式(7)进行整理得误差方程：

(8)

式中：误差方程系数阵

以上只是一对同名点列出的3个误差方程，对于n对同名点，则一共可列出3n个与此类似的误差方程式，进而得出法方程：

(9)

式中：法方程系数阵NBB=BTPB；常数项W=BTpl，P为观测值权阵，这里取单位阵，即P=I。

配准后i点的点位中误差为

(10)

式中:Qxixi、Qyiyi、Qzizi分别为i点在横坐标X、纵坐标Y和竖坐标Z方向的协因数。另外，在求解转换参数的过程中，可以通过迭代计算控制参数改正数在指定限差以内，求解坐标转换参数的最佳估值。

3 实验分析

堤防工程在防洪、灌溉、供水、航运、水保等方面发挥了巨大的社会效益、经济效益和环境效益。堤防工程的安全监测，不仅包括陆域的变形监测，也包括水域部分的地形变化，其真实场景的数字化仿真模型在堤防安全评价中发挥着重要的作用[21]。本文选取了长江南京河段梅子洲左岸中段作为实验对象，水域部分利用R2SONIC 2024多波束测深系统扫测，陆域堤防部分利用Faro Foucs3D地面三维激光扫描仪扫测，分别获取水域与陆域的点云数据，如图1所示。

图1 实验点云Fig.1 Experimental point cloud

利用地面控制网分别获取4对同名特征点在水域坐标系与陆域坐标系的坐标，其中陆域采用独立坐标系，水域采用BJ54坐标系，成果如表1所列。

表2 配准后同名点坐标及误差Tab.2 Coordinate and error of homonymic points after registration

对陆域点云中的所有坐标数据按求出的转换参数进行坐标转换，实现水域与陆域的点云配准。配准后的水陆联合点云如图2所示，可以看出：两者已位于同一坐标系下，实现了较为精确、严密的拼接，配准效果良好。在此基础上，对配准后的水陆联合点云进行精简、去噪等预处理操作并加以封装合并，通过曲面重构最终可以得到水陆一体化三维仿真模型。

图2 水陆点云的配准效果Fig.2 Registration effect of point clouds

4 结 语

随着测绘新技术与计算机仿真技术的发展，水域与陆域一体化的数字地形表达越来越趋于真实化与精细化，这类仿真模型在信息化测绘、洪灾模拟、淹没分析、灾情预警等工作中得到了越来越广泛的应用。由于两者参照坐标系的不同，要实现多波束获取的水域点云与地面LiDAR获取的陆域点云的联合仿真，首先必须解决两者之间的配准问题。本文在顾及水陆点云的弱重叠特征的基础上，以罗德里格矩阵为基础，详细地分析了罗德里格矩阵构建、参数初值解算、平差模型解算等过程，并以实测的水域与陆域点云数据，验证了该方法的精度与可靠性。实验证明：该方法不仅可以实现水陆点云的精确配准，且点云配准的单位权中误差和同名点的点位中误差均在毫米级。