H-ADCP代表流速与断面平均流速拟合精度研究

邓 山，胡 立，左 建，周 波，尤家伟

(1.长江水利委员会 水文局，湖北 武汉 430010； 2.长江水利委员会水文局 汉江水文水资源勘测局，湖北 襄阳 441000)

水平式声学多普勒流速剖面仪(Horizontal Acoustic Doppler Current Profiler，H-ADCP)利用声学多普勒原理进行流量测验[1]。通过将声学换能器固定安装在水下一定深度，实时监测水平层流速，采用代表流速法推算断面流量，从而实现流量在线监测。对于常年水深较大、水平层流速代表性较好的测站具有极大的实用价值，同时可为水资源监测管理、考核提供实时数据支撑[2-5]。

影响H-ADCP测验精度的外部因素较多，如测验断面及安装位置选择、设备选型与配置、不同水位条件下所测代表流速对断面平均流速的代表性等。这些因素都对H-ADCP测验精度具有较大的影响，应在安装前进行分析研究。

H-ADCP流量测验后处理主要分为以下3步：① 建立H-ADCP代表流速与断面平均流速的关系；② 根据水位面积关系用水位计算断面面积；③ 通过平均流速与断面面积计算出流量。其中第一步是关键也是难点所在，代表流速与断面平均流速关系的好坏直接决定了H-ADCP流量测验的精度。

目前H-ADCP代表流速关系拟合的主要方法为回归分析，美国地质调查局(USGU)推荐的H-ADCP代表流速关系拟合方法有简单线性回归、分段线性回归和加入水位等因素的多元回归等[6]。国内H-ADCP代表流速关系的拟合主要采用线性回归。王发君等利用回归方程建立了指标流速与断面平均流速关系[7]，鲁青等采用组合方式建立了多元回归关系，解决了南京站的流量在线监测问题[5]。但这些方法均没有考虑对H-ADCP代表流速关系拟合精度影响较大的三大问题：① 线性回归损失函数的选择；② 自变量(代表单元格)的选择；③ 比测数据的粗差剔除。本文主要针对以上3个方面问题，研究了以相对误差平方和最小作为损失函数、选择多自变量进行关系拟合、对数据进行粗差剔除等方法对代表流速关系拟合精度的影响，并以小河坝水文站H-ADCP代表流速关系拟合为例进行了验证。

1 H-ADCP代表流速关系拟合影响因素

1.1 线性回归损失函数

损失函数是将随机事件或其有关随机变量的取值映射为非负实数，以表示该随机事件的“风险”或“损失”的函数。在统计学和机器学习中被用于模型的参数估计。

使用通用软件进行关系拟合时，默认的拟合原理为最小二乘法，损失函数为误差平方和最小[8]，即：

(1)

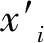
最小二乘法是一种经典方法，广泛应用于各个领域。但是由于最小二乘法本身的缺陷，使得它在水文关系拟合中存在一定的局限性。用最小二乘法进行代表流速关系拟合时，各点的相对估计误差往往分布不均匀，表现为大观测值的相对误差较小，小观测值的相对误差则很大，特别是当观测点间因变量量级相差较大时。而对于H-ADCP代表流速关系拟合而言，大流速数据和小流速数据的重要程度相当，数据质量需要用相对误差进行评价，故而用最小二乘法拟合的关系并不是最优解，通常不能满足定线误差要求。

为应对各行业的不同需求，最小二乘法有许多不同的改进方法，如加权最小二乘法[9]、最小二乘椭圆拟合算法[10]、相对误差最小二乘法算法[11-12]等。考虑水文测验的数据特点，对于H-ADCP代表流速关系拟合而言，更适合的损失函数为相对误差最小二乘法(相对误差平方和最小)[11]，即：

(2)

将线性回归的损失函数由误差平方和最小改为相对误差平方和最小，可以在一定程度上提高拟合结果的可靠性，并有效降低拟合公式的系统误差、随机不确定度及偏离数值检验的统计值，寻找到更符合水文测站实际的相关关系。

1.2 代表单元格的选取

目前，多数水文站H-ADCP代表流速关系拟合是通过Q-Monitor-H(流量通)[7]软件完成，主要步骤为：① 进行数据回放后选取数据相对稳定的单元格；② 输出不同单元格段的平均值；③ 再与实测断面平均流速进行关系拟合。采用一段单元格的平均值作为代表流速与断面平均流速建立相关关系，实际上是将多元回归问题简化为一元线性回归问题，通过这种简化后自变量变得单一，关系拟合更加简便。公式如下：

V断=aV代表+b

(3)

式中：V断为断面平均流速；V代表为H-ADCP某选定区间单元格代表流速平均值；a、b为系数。

但是，通过这种简化也难以拟合出最优线性关系，这是因为将代表流速平均，实际上是令选定区间单元格代表流速系数相同，相当于给多元回归的求解增加了多个约束条件，而这些约束条件对于提高代表流速关系拟合的精度是不利的。

在进行H-ADCP关系拟合时，可考虑直接选用各单元格流速进行关系拟合，将一元线性回归问题转化为多元回归问题，即：

V断=aiVi+ai+1Vi+1+…+anVn+b

(4)

实际上，H-ADCP每个单元格流速Vi在其垂线中的相对深度均不相同，同时各垂线平均流速对断面平均流速的代表性也各不相同，因而用各个单元格流速参与断面平均流速关系拟合，使其具有不同系数，也使得H-ADCP流量测验的物理意义更加明确。

1.3 粗差剔除

粗大误差是在一定的测量条件下，超出规定条件下预期的误差[13]。

H-ADCP关系率定产生粗大误差的原因主要有以下2个方面：① 客观原因。H-ADCP所测水层受船舶等引起的紊流影响；水中散射体浓度太大或太小；铁质物体影响ADCP磁罗经导致流向出现偏差。② 主观原因。使用的比测仪器本身存在的测验误差，如走航式ADCP比测时船速过快或不匀速等因素；还有人为计算错误、参数设置错误等。粗大误差的存在会使得关系线偏离，最终导致相关关系精度降低。而粗大误差不能仅因相对误差较大就删除，可采用拉依达准则(3σ准则)[14]进行剔除。应该注意的是H-ADCP比测数据一般为水文站基本测验数据，剔除前应对测点进行综合评判。

2 应用实例

2.1 小河坝水文站H-ADCP应用情况

小河坝水文站为嘉陵江重要支流涪江下游的出口控制站，位于东经105°50′，北纬30°11′，集水面积28 901 km2，是涪江下段基本控制站及国家基本水文站。该站测验河段顺直，河床组成主要为卵石夹沙，断面冲淤变化不大(见图1)，受下游2.5 km处潼南航电枢纽工程蓄放水影响。

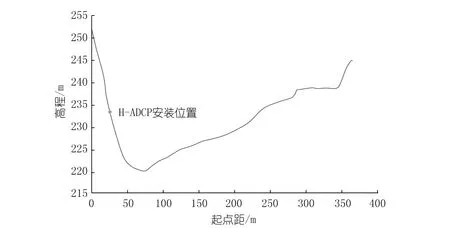
图1 小河坝水文站大断面及H-ADCP安装位置Fig.1 Main cross section and H-ADCP installation location in Xiaoheba station

小河坝H-ADCP选用Channel Master 300 kHz H-ADCP，安装位置位于起点距25.5 m、高程233.20 m处(低于潼南航电枢纽死水位235.5 m)。纵、横摇角度与初始采集安装角度值变化在±0.5°以内，且对安装位置进行了标记以确保放置位置固定。具体参数设置为：单元尺寸2 m，单元个数70个，盲区2 m，盐度为0，采样间隔5 min。本文主要利用现有条件下所获得的比测数据进行代表流速拟合关系研究，并未考虑设备安装、选型、参数设置、比测方案等因素对成果质量的影响。

采用走航式ADCP进行比测，比测时间为2019年5月14日至8月10日，共收集H-ADCP数据19 244组，走航式ADCP实测流量85次。率定期间水位变动范围为235.86～237.66 m；流量范围为132～5 460 m3/s；断面平均流速范围为0.053～2.550 m/s。

2.2 代表流速关系拟合方案制定

对小河坝站走航式ADCP、H-ADCP数据进行分析处理，计算出断面平均流速，挑选与走航式同时段的H-ADCP数据进行回放，检查回波强度曲线及水平层流速分布情况。经综合评定：4～24单元格段(离仪器距离9.4～51.4 m)流速分布均匀、回波信号稳定、流速紊动小、数据质量较好，选定用此区间的流速参与关系率定。剔除无效数据及受干扰数据，最终选定有效比测测次。点绘散点图后发现数据点呈较明显的带状，适合线性模型，且具有较高精度(见图2)。

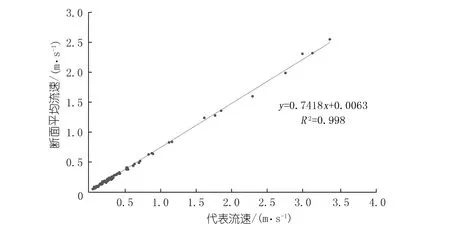
图2 小河坝站代表流速与断面平均流速关系Fig.2 Relationship between the representative velocity and the mean velocity in Xiheba station

采用线性回归进行小河坝站代表流速与断面平均流速关系拟合。为分析比较不同方法对代表流速关系拟合精度的影响，本文采用以下5种方案进行关系拟合。

(1) 方案1：常规方法。在数据稳定的4～24单元格中通过试算优选一定区间的单元格数据进行平均，用选定单元格平均流速与断面平均流速进行直线拟合。

(2) 方案2：剔除粗差后拟合。方法同方案1，但在确定拟合公式后采用3σ准则进行去粗差处理，然后重新进行关系拟合。

(3) 方案3：改变损失函数。在方案2的基础上采用相对误差平方和最小作为线性规划的损失函数进行关系拟合。

(4) 方案4：采用多元回归。在方案3的基础上采用多元回归求解，提取数据稳定的4～24单元格流速，与断面平均流速建立多元一次方程。为使关系式有物理意义，在进行规划求解时增加约束条件，使回归系数为非负值。经规划求解，选出最优方程，方程式中有9个单元系数非零，最终表达式为9元一次方程。

(5) 方案5：纯拟合分析。在方案4的基础上取消使回归系数为非负值的约束条件，进行纯数值拟合分析，经规划求解，最优方程式中21个单元系数非零，最终表达式为21元一次方程。

2.3 代表流速关系拟合精度评价

按照2.2节制定的5种方案进行关系拟合并统计拟合误差，系统误差与随机不确定度根据SL242-2012《水文资料整编规范》计算，结果列于表1。

表1 不同拟合方案误差Tab.1 Error values under different fitting schemes

注：在方案1～3中直线拟合选取的代表流速为单元格4～24之间的平均值，通过试算确定，与断面平均流速的拟合关系为最佳。表中随机不确定度取2倍标准差。

通过表1可以发现：方案1～4中，在常规方法拟合的基础上对数据进行粗差剔除；将损失函数由误差平方和最小改为相对误差平方和最小；将一元一次方程改为多元一次方程，每个步骤都能显著提高代表流速关系的拟合精度。系统误差从最初的-0.91%降到了-0.34%，随机不确定度从15.26%降到了11.85%。在方案5中，取消回归系数为非负值的约束条件虽可进一步提高拟合精度，但是通过分析发现，这样处理容易造成过拟合[15]，同时回归系数为负也让相关关系失去了物理意义，不推荐采用。

2.3.1粗差剔除对拟合精度的影响

由方案1到方案2，剔除粗差后拟合精度有了较大提升，系统误差由-0.91%降至-0.76%，随机不确定度由15.26%降至13.78%。但实际上在方案2～5中进行去粗差处理后均只剔除了一个样本数据，可见粗大误差对关系拟合精度影响较大。

2.3.2损失函数对拟合精度的影响

从方案2到方案3，将线性回归的损失函数由误差平方和最小改为相对误差平方和最小，系统误差由-0.76%降至-0.44%，随机不确定度由13.78%降至13.39%。虽然精度指标的提升并不显著，但仍然非常有必要，一方面是其在原理上更加符合水文关系拟合的需求，另一方面是当样本容量增大、样本间量级相差较大时两种损失函数对拟合精度的影响将会更加明显。

2.3.3代表单元格选取对拟合精度的影响

从方案3到方案4，通过将回归方程由一元回归优化为多元回归，系统误差由-0.44%降至-0.34%，随机不确定度由13.39%降至11.85%。

整体而言，方案4通过粗差剔除、将损失函数改为相对误差平方和最小、采用多元回归等手段，成功将误差指标降低到了规范要求以内，推荐采用此方案。

2.4 代表流速关系拟合推荐方案

2.4.1拟合结果

方案4中，H-ADCP代表流速采用5，6，13，14，17，20，21，23，24单元，拟合公式为

V断=0.07650V5+0.04650V6+0.00014V13+0.00059V14+0.03740V17+0.06760V20+0.19060V21+0.30750V23+0.051850V24+0.00510

(5)

相对误差分布如图3所示，可以看出拟合精度较好，所有样本计算相对误差均未超过15%，能够较好地拟合指标流速与断面平均流速的关系。

图3 相对误差分布Fig.3 Relative error distribution

2.4.2成果检验

需要注意的是，进行多元回归拟合时，自变量数量的增加会导致计算速度变慢、也可能造成过拟合。可将数据分为率定样本和检验样本，防止过拟合现象发生。本次研究随机预留了5组数据作为检验样本，检验结果列于表2。结果表明：检验误差均不超过9%，推荐方案的拟合关系精度较好，能够满足水文测验精度要求。

表2 检验样本计算结果Tab.2 Calculation results of test samples

3 结 论

本文对H-ADCP代表流速与断面平均流速关系拟合过程中,线性回归损失函数的选择、代表单元格的选取、粗大误差的剔除等技术进行了研究。并以小河坝水文站为例，设计了5套方案，研究了上述方案对代表流速关系拟合精度的影响。结果表明：

(1) H-ADCP代表流速关系率定时，粗大误差对关系拟合精度影响较大，必须进行剔除；应选择相对误差平方和最小作为损失函数，不仅更符合水文实际，也能提高拟合精度；将回归方程由一元线性回归优化为多元线性回归，使H-ADCP流量测验的物理意义更加明确，并能有效提高拟合精度。

(2) 对小河坝水文站代表流速关系拟合而言，最优方案是以相对误差平方和最小为损失函数，提取4～24单元格流速，与断面平均流速建立多元一次方程，并进行去粗差处理，同时约束回归系数为非负值。该方案将代表流速关系的系统误差和随机不确定度都降低到了规范要求以内，并通过了预留样本检验。

(3) 本文的研究成果可为H-ADCP及其他流量在线监测设备的代表流速关系拟合提供参考。