基于PCA-RVM的TBM掘进速度预测模型研究

张 研，曾建斌，邓雪沁

(1.桂林理工大学 广西岩土力学与工程重点实验室，广西 桂林 541004； 2.桂林理工大学 土木与建筑工程学院，广西 桂林 541004)

隧道掘进机(Tunnel Boring Machine，TBM)施工的优点在于施工快捷、优质可靠、安全环保，尤其适合中长隧道的施工，未来硬质岩体的隧道施工将普遍采用此方法[1-2]。为使该方法在工程实际中取得最佳效益，人们越来越重视施工进度及施工成本之间的关系。合理的掘进速度有利于维持围岩稳定性，降低施工造价，这对TBM隧道安全、高效施工具有重要意义[3]。

自20世纪70年代以来，涌现出一系列TBM掘进速度预测模型，包括单因素预测模型、综合预测模型、岩体分类预测模型、概率模型等[4]。其中，以CSM和NTNU模型为代表的综合预测模型应用较为广泛。CSM模型来自室内线性切割试验，但未充分考虑岩体中节理裂隙带来的影响；NTNU模型虽然较全面地考虑了各影响因素，但采用的某些指数不适用于广泛的岩石试验，限制了该模型的应用。挪威学者Barton[5]根据调研大量地下开挖工程稳定性实例提出了Q模型，该模型考虑了6项质量评价指标后，将影响掘进机和岩体相互作用的因素考虑进去，通过分析来自隧道施工的大量数据，对Q模型加以改进，确定了QTBM模型，但该模型列出的部分参数对掘进速度预测结果无实质性影响。Nelson[6]提出的概率模型采用统计分析方法能够对不同阶段的施工时间与费用数据进行概率形式的估算，但它在相似性模拟中存在一定的局限性。

近些年，随着计算机技术的高速发展，针对上述模型存在的不足，许多学者基于人工智能技术提出了一些新的隧道TBM掘进速度预测模型，它们能够弥补传统预测模型的不足。其中，以Acaroglu等提出的模糊逻辑(FL)模型、温森等提出的Monte Carlo-BP神经网络预测模型以及Mahdevari等基于支持向量回归(SVR)提出的TBM掘进速度模型为代表[7-9]。但以上模型本身还是存在一些缺陷，导致模型在应用中受到限制，如支持向量回归核函数以及参数难以确定，BP神经网络预测能力对初始训练样本的依赖性强[10]。因此，更加准确、合理的智能预测模型亟待提出。

相关向量机方法(Relevance Vector Machine，RVM)是近年来流行的机器学习方法，它具有高精度、参数自适应获取和适应小样本问题等优势，可以建立各种复杂工程问题的预测模型[11]。然而当输入样本影响因素(即样本维数)较多时，会降低RVM模型学习效率，增加计算成本。本文采用主成分分析法(Principal Component Analysis，PCA)提取数据特征、降低数据维度[12]，以降维数据作为RVM的输入量进行预测，可将RVM解决小样本复杂问题的突出优势体现出来[13]。通过RVM模型建立降维后各因素与TBM掘进速度之间的非线性映射关系，建立基于PCA-RVM的TBM掘进速度预测模型，为掘进速度预测提供了一条新途径。

1 基本原理

1.1 主成分分析法

主成分分析法的主旨在于降维，通过对初始观测样本的一系列处理，保留对样本总体贡献率较大的因素，剔除贡献率较低的因素，以此得到低维度的新变量系统[14]。设总体观测样本含有m个样本，对n个变量进行观察，构建的主成分分析观测模型如式(1)所示：

(1)

对输入数据标准化处理可避免因数据量纲造成的模型精度问题。假定观测模型的相关系数矩阵为R=(rii)，将样本矩阵Xm×n的二维向量设为Xi与Xj，则rij可由标准化后样本数据的协方差矩阵转化得到：

(2)

用雅克比方法求特征方程|λE-R|=0的m个非负特征根λ1≥λ2≥…λm≥0。

经过主成分分析，初始变量x1,x2,…,xt变换成t个综合指标因子y1,y2,…,yt，表达式如下：

(3)

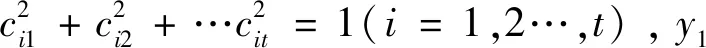
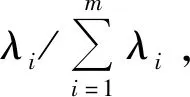
1.2 相关向量机

tn=y(xn;ω)+ξn

(4)

式中：ω为权值向量，ξn为零均值，方差为σ2的附加高斯噪声，且相互独立。故p(tn|x)=N(tn|y(xn),σ2)服从高斯正态分布，且其分布是由tn、y(xn)的值以及方差σ2所决定的。同时，y(x)的值是由核函数所决定的。RVM的原理如图1所示。

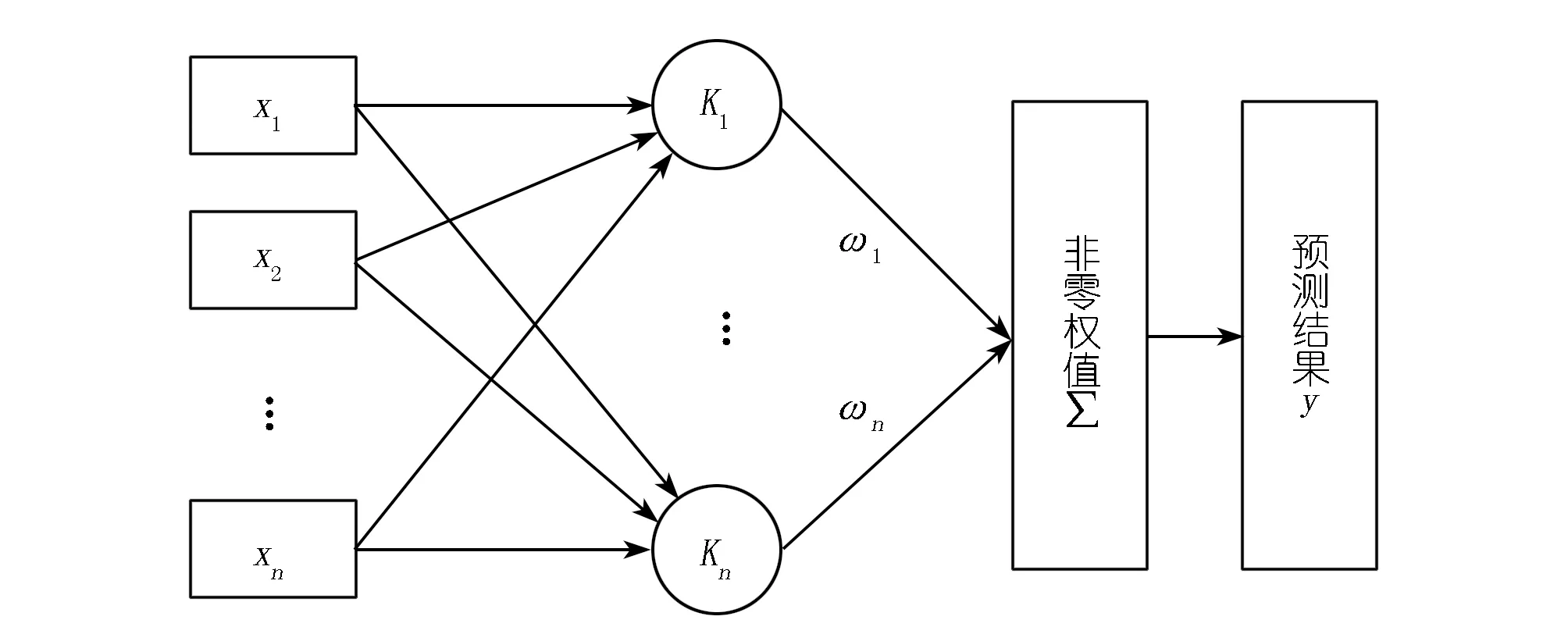
图1 RVM模型工作原理Fig.1 Working principle diagram of the RVM model

本文采用局部线性插值能力较强的高斯核函数用于TBM掘进速度的预测，其形式为

(5)

式中：xc为核函数中心，σ为函数的宽度参数。

由于前文假设tn相互独立，则训练样本集的似然函数可采用下式表达：

(6)

式中：t=(t1,t2,…,tN)T为目标向量，参数向量为ω(ω0,w1,…,ωN)T，Φ为N×(N+1)维由核函数组成的矩阵，Φ=[φ(X1)φ(x2)…φ(xN)]T，φ(xn)=[1,K(xn,x1),K(xn,x2),…，K(xn,xN)]T。

(7)

式中:α是决定权值ω的先验分布的N+1维超参数。因为高斯正态分布方差倒数的共轭概率分布服从Γ分布，假定超参数α和噪声参数σ2服从Γ先验概率分布：

P(αi)=Γ(a,b)

(8)

P(σ2)=Γ(c,d)

(9)

Γ(a,b)=Γ(a)-1baaa-1e-ba

(10)

(11)

为使得到的超参数相对均匀，通常取a=b=c=d=0。

由贝叶斯原理可以得到后验分布概率的关系式：

(12)

(13)

式中：P(ω,α,σ2|t)用积分的方法不能求解，因此可以将上式分解为

P(ω,α,σ2|t)=P(ω|t,σ,σ2)P(α,σ2|t)

(14)

经变换得出权重ω的后验分布的表达式：

(15)

其后验均值和协方差可以分别表示为

μ=σ-2ΦTt

(16)

∑=(σ-2ΦTΦ+A)-1

(17)

式中：A=diag(α0,α1,…,αN)为对角矩阵。

在更新超参数迭代学习的过程中，产生的相关向量可反映初始训练样本特征，与用来预测的样本无关[17]。在初始样本学习的过程中，α和σ2是两个必要的超参数，运用RVM方法进行学习时，超参数可自适应获取。在超先验的条件下，取P(t|α,σ2)最大。

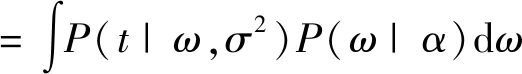
(18)

可以运用MacKay法求解α和σ2的值，令式(18)为零，通过求超参数的偏导得到：

(19)

(20)

γi=1-α∑ii

(21)

式中：μi是第i个后验平均权重，∑ii是第i个对角元素。在求解超参数的过程中，将趋向无穷大的超参数去除，以获取具有稀疏性的相关向量机模型。

设待测样本为x*，预测值为t*，则待预测的数据结果可由下式求解得到：

(22)

由于式(22)中等号右侧的被积函数都服从于高斯正态分布，故t*也服从高斯正态分布

(23)

2 基于PCA-RVM的TBM掘进速度预测模型构建

2.1 TBM掘进速度影响因素的主成分分析

为平衡TBM掘进速度与施工成本的关系，提出一种合理可行的预测模型十分必要。依照前述方法进行主成分分析，得到各主要影响因素之间的关系，利用累计贡献量这一指标确定需要保留的主要因素，将这一结果输入到RVM模型，通过模型对样本进行学习，输出TBM掘进速度的预测结果。本文以文献[8]中的5个影响因素作为TBM掘进速度(PR)主要影响因子，分别为完整岩石的单轴抗压强度(UCS)、巴西试验劈裂抗拉强度(BTS)、软弱结构面的平均间距(DPW)、冲击试验压头的最大荷载与相应的位移的比值(PSI)和隧道轴线与软弱结构面之间的夹角(α)。以上影响因素可通过岩块力学性质试验或现场监测获取，操作方便快捷。将文献[8]中的TBM掘进速度数据进行整理，以1～15号数据作为学习样本，16～25号数据作为预测样本，如表1所示。

相关向量机是监督式学习的一种，为此需要验证表1中训练样本集与预测样本集相互独立且具有联合概率分布。KS-检验(Kolmogorov-Smirnov test)可通过比较样本的经验分布函数和理论分布函数作拟合适度检验。经检验，在0.05显著性水平下，每个输入量显著地来自正态分布总体，满足RVM模型对输入样本的要求。

表1 TBM掘进速度数据集Tab.1 Data set of TBM penetration rate

对表1中数据进行标准化处理，输出检验结果，用KMO来反映各变量的相关程度，用Bartlett球形检验来验证其矩阵是否为单位矩阵。通过计算得到KMO值、Bartlett球形检验中sig值分别为0.753和0.016，结果满足进行因子分析的条件。结合本文所述两种原理的特征，采用主成分分析法对表1中的各输入变量进行降维处理，使RVM在处理小样本问题上的优势充分展现。利用主成分分析法对影响因素进行分析，得到的相关系数矩阵如表2所列。

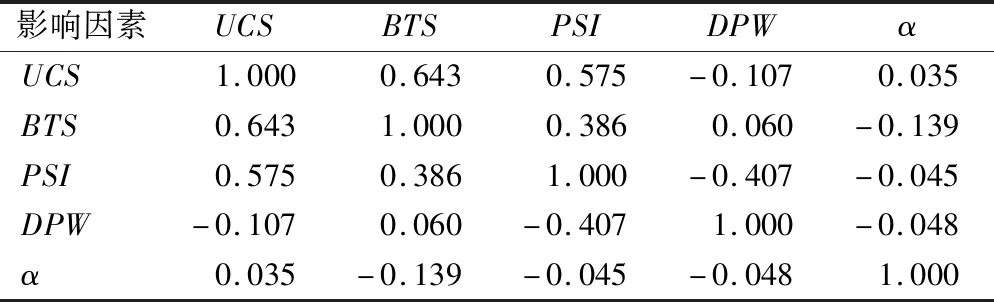
表2 相关系数矩阵Tab.2 Matrix of correlation coefficient

由表2可知：前3个影响因素的相关系数较大，反映它们之间具有较大的线性相关性。如：UCS与前3个影响因素的相关系数分别为1.00，0.643和0.575，其线性相关性依次降低；而与后2个影响因素的相关系数为-0.107和0.035，表现为负相关和几乎不相关。由此可初步判定：UCS与前3个影响因素相关性较大。为保证原始信息提取充分，确保线性变换后的新数据作为输入样本不影响相关向量机模型的稳定性，需进一步进行主成分分析。用软件进行主成分分析得到的总方差解释如表3所列。

表3中，前3个主成分的方差累计贡献率已达86.137%，所以认为前3个主成分能够反映全体变量包含的信息。各主成分的方差贡献率以及累计贡献率如图2所示。

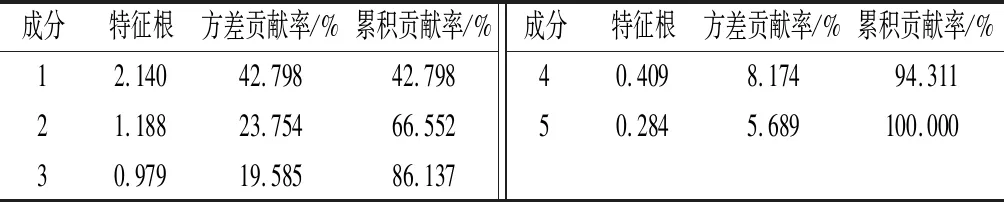
表3 总方差解释Tab.3 Explanation of total variance

因子载荷是第i个变量在第j个主成分的权重，反映了该变量在对应的主成分上的相对重要性。表4中的因子载荷矩阵反映了提取的主成分与不同影响因素之间的密切程度。

表4 因子载荷矩阵Tab.4 Factor load matrix

利用主成分分析法实现了对原始影响因素的降维，提取的3个主成分经线性变换公式获取新的变量表达式：

(24)

第一主成分y1所对应的方差贡献率最大，是反映与PSI、UCS、BTS有正相关的主成分指标，是岩石的单轴抗压强度、巴西试验劈裂抗拉强度和冲击试验压头的最大荷载与相应位移的比值的综合反映，代表该主成分与掘进部位岩石的力学性能有较大相关性。第二主成分y2对应的方差贡献率次之，主要反映影响因子α与该主成分有较大的相关性，而影响因子BTS与该主成分具有较大的负相关性，该指标主要度量隧道轴线与软弱结构面之间的夹角和岩石抗拉强度。同样的，第三主成分y3更能反映岩石抗压强度UCS和结构面间距DPW中包含的信息。

通过主成分分析，以矩阵构成的新模型代替原先的矩阵，有效降低了数据维数。降维后的3个主成分包含了5个影响因素的绝大多数信息，因此可作为TBM掘进速度预测的输入量。

2.2 TBM掘进速度预测模型

采用经主成分分析法降维后3个影响因素对应的数据集作为输入值，以掘进速度(PR)作为输出值。对上述数据标准化处理后，选择局部插值能力较强的高斯核函数对1～15号共15组样本数据进行掘进速度的验证。为了获得更有效的模型，选取最优核宽度，分别选取0.16，0.18，0.20，0.22，0.24，0.26，0.28作为高斯核宽度对模型进行对比。初始化程序后对不同高斯核宽度下验证结果的最大相对误差进行计算和对比，结果见图3。显然，高斯核宽度，迭代次数为500时，得到的最大相对误差最小。各样本掘进速度的实测值、BP神经网络预测值、RVM模型预测值以及PCA-RVM预测值的输出结果如表5所列。

图3 掘进速度对应不同高斯核宽度的最大相对误差Fig.3 Maximum relative errors of different core widths corresponded with excavation rate

由表5可以看出：基于PCA-RVM模型得到的相对误差均小于其他模型，其相对误差值最大的21号样本仅为0.41%，而BP神经网络方法预测值的最大相对误差高达17.24%，直接采用RVM方法其预测结果的最大相对误差为2.93%。采用PCA-RVM模型的预测结果均好于其他两种方式。为了更好地观察不同模型输出的预测值，将表4中3种方法的输出的掘进速度预测值进行对比(见图4)。

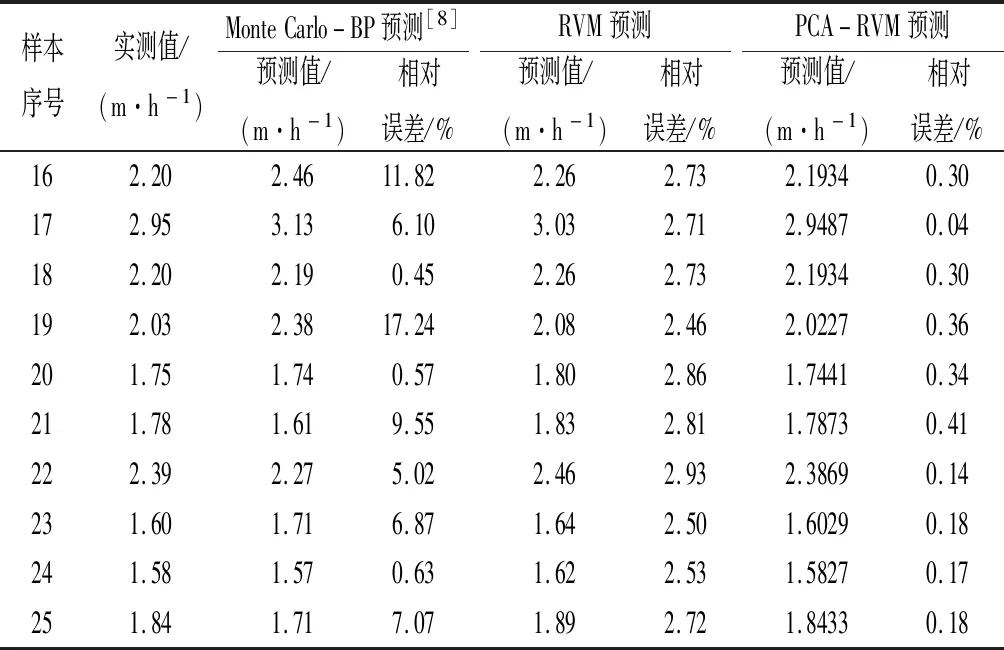
表5 不同方法的预测结果比较Tab.5 Comparison of prediction results by different methods

图4 不同方法掘进速度预测值对比Fig.4 Comparison of prediction results by different methods

由图4可见：PCA-RVM模型各预测值几乎与实际TBM掘进速度重合，而BP神经网络预测结果偏离较大，RVM模型预测值次之。从图形可直观地看出BP神经网络预测值中16，19，21号样本偏离明显，PCA-RVM模型的预测精度更高。本文还采用平均相对误差ARE和均方差FMSE来反映各模型预测结果的整体误差水平与离散程度，其计算公式为

(25)

(26)

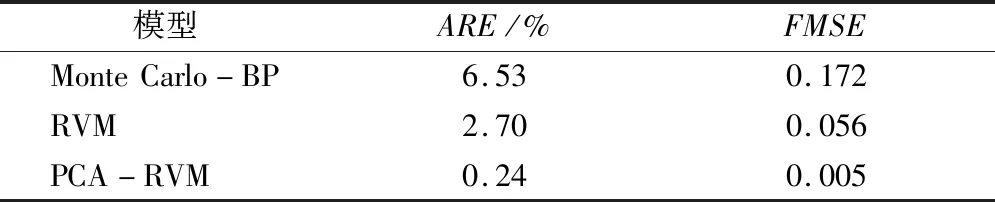
表6 不同模型ARE与FMSE对比Tab.6 Comparison of ARE and FMSE by different models

由表6可见：本文提出的PCA-RVM模型计算得到的平均相对误差为0.24%，均方差为0.005；而BP神经网络预测模型，其平均相对误差为6.53%，均方差为0.172。由此可见，与BP神经网络和RVM模型相比，基于PCA降维后得到的数据集更有利于RVM模型的预测，其预测精度高，离散型小，结果可信。

3 结 论

本文提出一种基于PCA-RVM的TBM掘进速度预测模型。通过PCA将5个影响因素降维成3个独立主成分变量，采用RVM建立主成分变量与掘进速度间的非线性映射关系，主要结论如下。

(1) 通过PCA对原始数据进行降维处理，使得降维后的数据基本能够保证原数据信息的完整性；采用RVM建立降维主成分变量与TBM掘进速度间的映射关系，进而预测TBM的掘进速度，其预测结果精确、拟合程度高、离散性小，为TBM掘进速度的准确获取提供一条新途径。

(2) 3种模型的预测结果表明，采用PCA-RVM进行TBM掘进速度预测得到的平均相对误差和均方差均低于BP神经网络及RVM模型，本文提出的模型在回归预测问题上比BP神经网络和RVM模型更有优势。

(3) 本文模型的提出是建立在获得工程实际TBM掘进速度数据的基础上，通过广泛收集样本数据，以此建立预测模型，对优化模型参数，提高模型的适用性和准确度有重要意义。