连续波泥浆脉冲发生器阀口形状拓扑优化设计

王 鹏, 田 懿, 吉进元,冯 定, 涂忆柳

(1.长江大学机械工程学院,湖北荆州 434023; 2.湖北省油气钻完井工具工程技术研究中心,湖北荆州 434023;3.四机赛瓦石油钻采设备有限公司,湖北荆州 434024)

由于地质导向和地层油藏评估的需求,井下信息需上传至地面供工程师进行分析,而连续波泥浆脉冲传输方式因其较高的传输速率[1-2]和相对低廉的价格,目前在无线传输中已成为主流[3]。为提高脉冲信号传输的速率和质量,国内外学者开展了大量研究。在提高信号传输速率方面,如采用钻井液压力正交相移键控调制解调[4]、多进制数字频率调制[5]、OQPSK调制[6]等方式等提高数据上传速率。在提高信号质量方面,一般认为连续波泥浆脉冲发生器的阀口形状将直接影响泥浆脉冲信号质量[7],为了寻求阀口形状与压力波的关系,进而设计出符合要求的阀口形状。因此，相关研究主要集中在对某一种阀口形状的设计与优化,其中阀口的形状主要有梯形[8-9]、三角形[10-15]、扇形[16]、圆形[5]、曲线[17]等。此外,在阀口形状设计方法上,主要采用的是波形最大相似理论[9],假定转阀或定阀的形状已知,或两者形状上互补,即最小过流面积为零[16],在极坐标下构建阀口的几何形状方程,通过分段积分的方式,建立不同时刻的过流面积与压力波的关系,并以其与理想压力波的相关系数最大原则,求得阀口几何形状曲线的方程形式。但是,由于阀口的曲线方程形式与面积关系推导过程非常复杂,目前主要采用外轮廓曲线方程进行阀口设计,难以实现其他形式的阀口形状设计,如内轮廓形状阀口设计、动定阀形状均未知的设计等。基于此,笔者结合连续体拓扑结构的思想,将阀口的设计区域转化成0-1拓扑结构,将阀口的旋转运动简化为矩阵平移运算,建立任意阀口形状结构参数与过流面积、压力波的关系,并通过案例分析验证该方法的可行性。

1 阀口前后压力差计算

连续波泥浆脉冲发生器的动阀在旋转过程中,泥浆由于被不断地遮挡和释放而造成阀口前后产生压力差,生成高、低压力波形,其波形产生原理如图1所示。

1.1 理论压力波

流经连续波泥浆脉冲发生器的流体,在阀前后会产生压降Δp,该压降的精确计算需借助于计算流体动力学(CFD)求解,但由于泥浆脉冲发生器阀口结构参数未知,因此在设计中无法直接采用CFD进行求解,一般采用薄壁压降计算模型[18]进行简化计算,表示为

(1)

式中,A为转阀的通流面积,m2;Q为钻井液流量m3/s;Cd为转阀阀口的流量系数;ρ为钻井液密度,kg/m3;Δp为钻井液流经转阀所产生的压降,Pa。

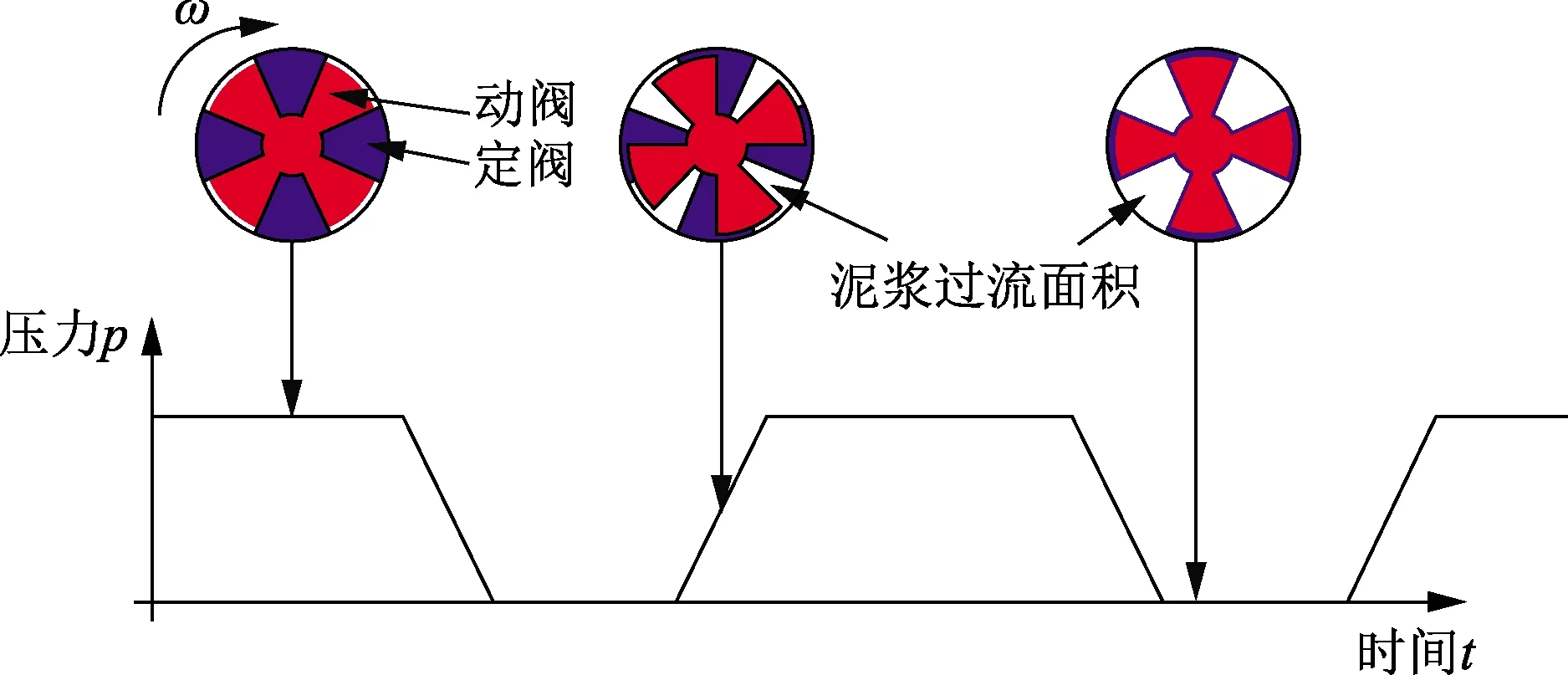
图1 连续波泥浆脉冲发生器工作原理Fig.1 Working principle of continuous-wave mud pulse generator

1.2 理想压力波

随着时间的变化,流经连续波泥浆脉冲发生器所产生的压降Δp,会生成压力波信号。该信号一般为接近于矩形波的梯形信号,该信号可以被分解成基本的谐波信号。然而,这种信号在井筒中传输时,信号中的谐波分量衰减很快,这会导致信号损失,造成地面信号解码困难。如果将信号能量集中在某个基本谐波信号频段范围,则可以减少衰减,从而减少地面解码的工作量,因此选择简谐波信号作为理想压力波。

(2)

式中,Δpmax和Δpmin分别为阀口前后最大和最小压力差,Pa;N为动阀的阀瓣个数;ω为动阀的转速,rad/s;φ为压力波信号的初始相位,rad。

2 阀口形状拓扑化处理

2.1 设计区域的拓扑结构

将动、定阀设计截面进行网格划分,角度划分间隔需要与标准的正弦波采样间隔进行匹配,具体关系为

dt=dθ/ω.

(3)

式中,dt为标准的正弦波采样时间间隔,s;dθ为角度划分间隔,rad。

在0°位置处,将设计截面剪开,并将网格以正方形网格形式展开,形成设计的拓扑区域。在区域水平方向,是沿着角度方向依次增大;区域竖直方向,沿着半径方向依次增大。区域内单元值为0,代表实体,遮挡流体;1代表空,释放流体。对于设计对象,设计的区域展开后可以表示为如图2所示,图中黑色区域单元表示为0,白色区域单元为1。

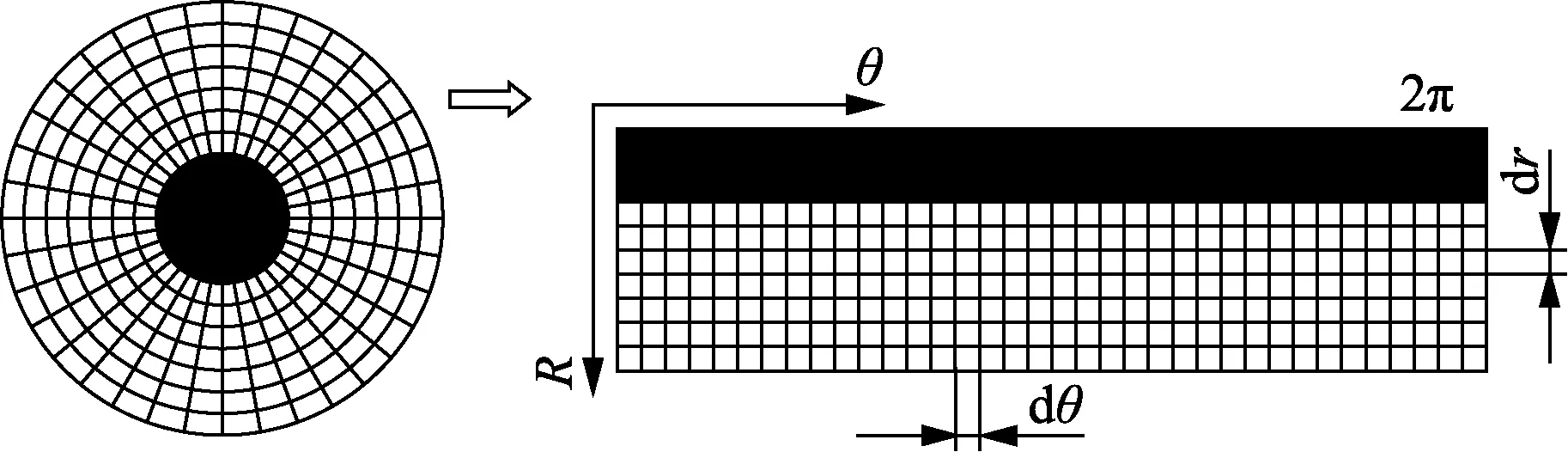
图2 阀口形状拓扑区域Fig.2 Topology regions of valve orifice shape

经过该方法处理后,动、定阀的设计区域可以分别转化成一个0-1的二维矩阵。在该截面处,每一格所占的面积可以组成一个新的二维矩阵,每一行对应的单元面积相等,取矩阵中某一列单元对应的面积,构成单元面积矩阵Am。

2.2 动定阀拓扑结构构建

阀口的形状选用最基本的几何形状组合,如直线、圆,组合构成光滑的曲线。以半径方向为纵坐标,范围[0,R];角度方向为横坐标,范围[0,θ],形成坐标系。将基本几何形状函数对应的半径和角度在设计域内离散化,将所得的离散曲线以r轴为对称轴进行对称操作,即可得到整个阀口的形状,如图3所示。该方法可以得到动、定阀的0-1矩阵,若图示对应定阀形状,则经过逻辑取反则可以得到动阀的形状。由于曲线函数的任意性，曲线可能会超出规定区域。将曲线上点(r,θ)离散后得到点(rn,θn)，若出现rn值过大而越界，则θn所在列的值均为1或0；若出现rn值过小而越界，则θn所在列的值均为0或1；其他情况，θn所在列的值自rn以下均为1或0。

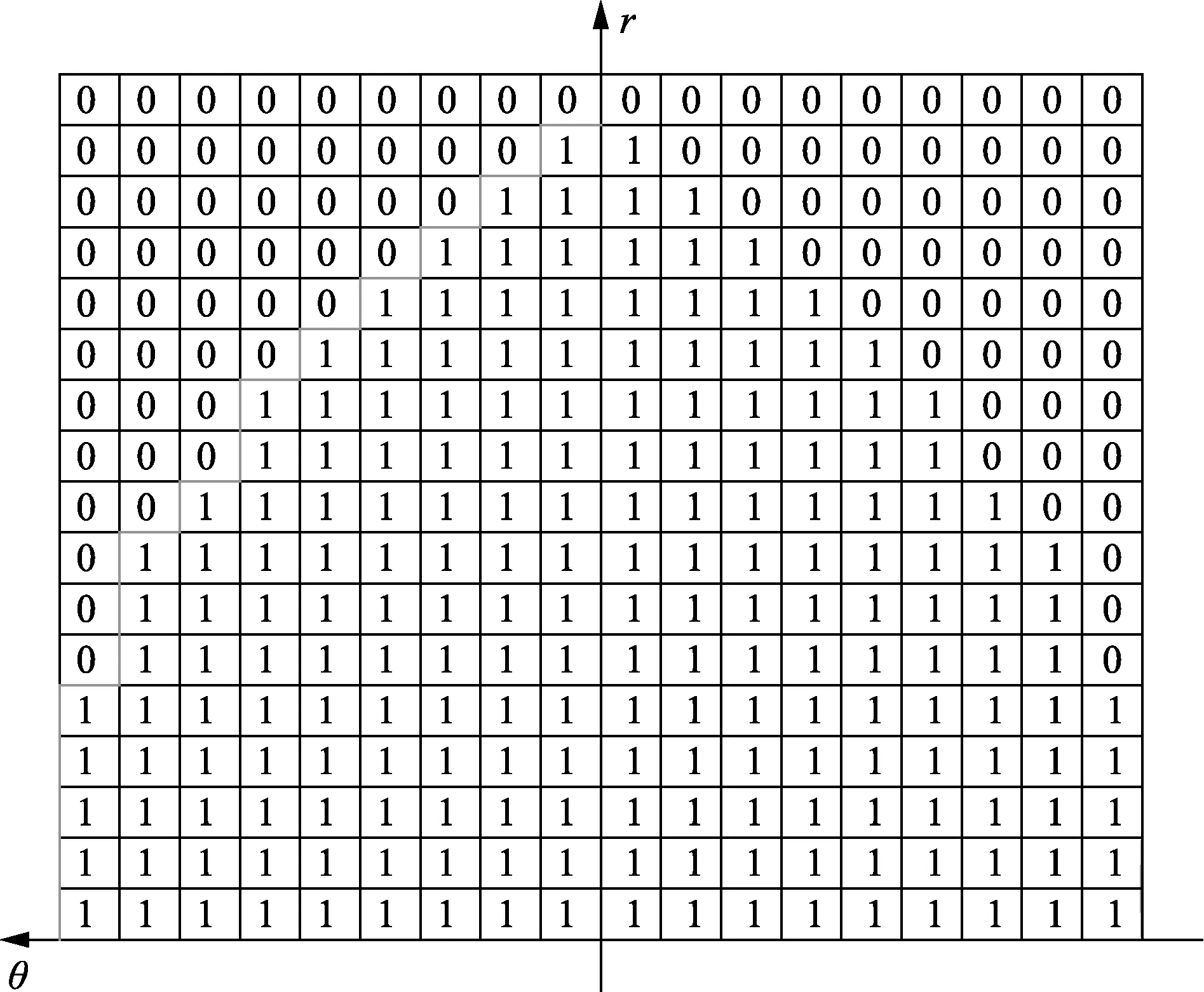
图3 阀口形状拓扑结构Fig.3 Topological construction of valve orifice shape

2.3 过流面积计算

连续波泥浆脉冲发生器的动阀在旋转过程中,过流区域的面积计算转化成动阀平移矩阵和定阀矩阵的运算,不同时刻的过流面积A(t)为

(4)

式中,R为i行j列的动阀矩阵;S为i行j列的定阀矩阵;R(t)为t时刻动阀平移α(α=ωt)角度后的动阀平移矩阵。

由式(4)可以计算不同时刻阀口的过流面积,从而求出该时刻对应的压降变化,得到随时间变化的压降信号Δp(t)。

2.4 阀口形状的评价指标

为使得不同动、定阀结构对应的理论压力波趋近于理想的压力波,借助于信号的相似理论,使用信号的互相关系数[9]作为评价阀口形状的指标:

(5)

式中,Δpi为第i次采样时间dt下的压差;μΔp和σΔp分别为所有采样压差的平均值和标准差;μΔpst和σΔpst分别为所有理想采样压力的平均值和标准差;M为采样压力数据个数。

利用信号的相关性分析,可以得到任意曲线形状对应的压降信号与理想压力波信号的相关系数,相关系数越接近于1,则所得的阀口形状越符合设计要求,这个可以做第一个目标函数f1。

设计形状对应的结构方案,产生的理论压力波应该满足最大和最小压力波的要求,则可得另外两个目标函数:

f2=|max(Δp)-max(Δpst)|,

f3=|min(Δp)-min(Δpst)|.

(6)

3 设计流程

假设定阀和动阀的阀口形状为对称几何形状,控制这些基本形状的变量为(R,θ),其中定阀对应的变量为(rs1,θs1),…, (rsn,θsn);动阀对应的变量为(rr1,θr1),…, (rrn,θrn)。通过调节变量(R,θ),可以得到不同的动、定阀拓扑结构,利用阀口形状的评价指标构建评价函数f(R,θ),对不同的形状设计结果进行多目标评价,借助于遗传算法可对此问题进行优化求解。由于遗传算法得到的结果不唯一,因此一般需要多次计算,选取评价函数值较优的结果,具体设计流程见图4。

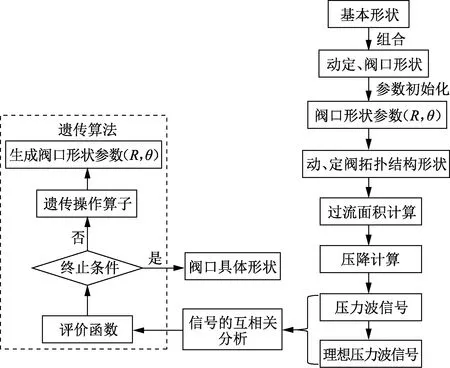
图4 阀口形状设计流程Fig.4 Design flow chart of valve orifice shape

4 计算实例

工况参数:钻井液流量0.025 m3/s,密度1 380 kg/m3,压力波信号最大值2 MPa,最小值0.27 MPa,阀口的流量系数0.7,动阀的瓣数4,旋转速度240 r/min,设计阀口截面直径为90 mm。通过阀口形状设计流程计算后,得出的定阀结构参数为:r1=18.450 mm,r2=35.100 mm,θ1=0.262 rad,θ2=0.489 rad,θ3=0.209 rad。转阀结构参数为:r1=15.300 mm,r2=41.400 mm,θ1=0.454 rad,θ2=0.541 rad,θ3=0.576 rad,对应的拓扑结构图如图5所示。设计的定、转阀形状及产生的压力信号与理想压力信号曲线如图6所示。理想结构所产生的最小、最大过流面积分别为663.450和1 803.690 mm2,产生的最小和最大压力分别为0.270和1.999 MPa,压力波信号与理想信号的相关系数为1;拓扑结构产生的最小、最大过流面积分别为671.920和1 721.070 mm2,产生的最小和最大压力分别为0.297和1.949 MPa,压力波信号与理想信号的相关系数为0.982。

可以看出,拓扑结构设计出的连续波泥浆脉冲发生器动、定阀的最小过流面积增大1.277%,最大过流面积减小4.581%,最小压力增大10.000%,最大压力减小2.501%,相关系数为0.982,减小1.800%,非常接近于1。从图6中也可以直观地看出,阀口形状拓扑优化设计结果与标准的正弦波非常接近,这也较好地验证了该方法的可行性。

图5 动定阀的拓扑结构Fig.5 Topological structure of rotor and stator valve

图6 压力信号随时间变化曲线Fig.6 Variation curve of pressure signal at different time

5 结 论

(1)验证了将阀口形状设计问题转化成拓扑结构设计方法的可行性。借助于本方法,动、定阀口形状设计不再局限于外轮廓形状的设计,而且可以同时设计动、定阀口的形状。

(2)与传统的分段积分求解动阀旋转下的过流面积方法不同,本方法只需将动阀口的拓扑矩阵按时间进行平移操作,与定阀矩阵相乘,即可计算出不同时刻的非遮挡面积(过流面积)。