木楔效应在水平定向钻回拖力预测中的分析与应用

蔡亮学, 王勐龙, 冯 宇, 徐广丽

(1.西南石油大学石油与天然气工程学院,四川成都 610500; 2.油气消防四川省重点实验室,四川成都 611731;3.西安长庆科技工程有限责任公司,陕西西安 710018)

与管线的传统开挖敷设技术相比,水平定向钻(HDD)技术在提高工效、降低造价、保护环境等方面均有独特优势,自Martin[1]首次应用该技术成功穿越帕哈罗河敷设一条管径100 mm、长度220 m的排污钢管以来,HDD技术在国内外的通讯电缆、油气管道、供水管道与电力电缆等市场中得到迅速推广[2-3]。目前,大中型HDD穿越工程的穿越失败风险较高,仍存在大量技术问题亟待解决。其中回拖力预测可为穿越工程设计、钻机型号选择、管道在施工中的稳定性评价、回拖减阻工艺制定等关键环节提供依据,受到大量学者的关注[4-6],但各种预测方法的计算结果尚难以满足工程应用需求[7-8],原因之一是未充分考虑管道回拖过程中管土耦合以及导向孔对管道的夹持作用,而管土间摩擦力是回拖阻力的主要组成部分[9],导致预测结果与工程实际有较大偏差。笔者采用Winkler模型描述土壤,按照有限元分析方法建立管土耦合作用分析模型,讨论外载荷、地基反力系数、管材弹性模量、扩径比、椭圆扁率等参数影响木楔效应系数的规律,并基于两项HDD穿越工程实例考察木楔效应对回拖力预测的影响。

1 木楔效应分析模型

1.1 物理模型与单元刚度矩阵

HDD施工中导向孔横截面的理想形状为圆形,小型HDD工程的导向孔横截面可近似视为圆形[10];而对于大型HDD工程,由于穿越曲线中含有较多曲线段,钻柱对导向孔有较严重的“啃边”现象[11],致使导向孔横截面为梨形。

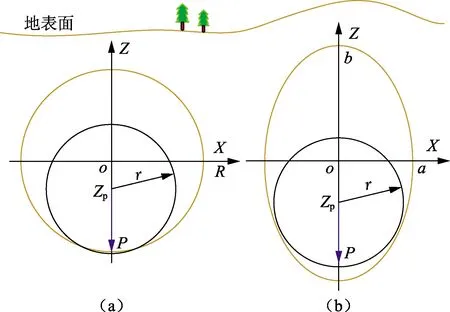
图1 物理模型示意图Fig.1 Schematic diagram of physical model

采用椭圆描述梨形截面,建立两种分析模型如图1所示。设半径为r,壁厚为t,管材弹性模量为E的无限长管道分别位于半径为R的圆形Winkler地基,短、长半径依次为a、b的椭圆形Winkler地基中,管道承受垂直向下的体积力载荷P。将管土耦合作用视为平面应变问题,取单位长度管道进行分析,建立笛卡尔直角坐标系,圆形、椭圆形地基的圆心分别为原点。由于管道承受的载荷关于Z轴对称,取其1/2,按等角度划分为n个单元,各单元长度相等,记为l,如图2所示。

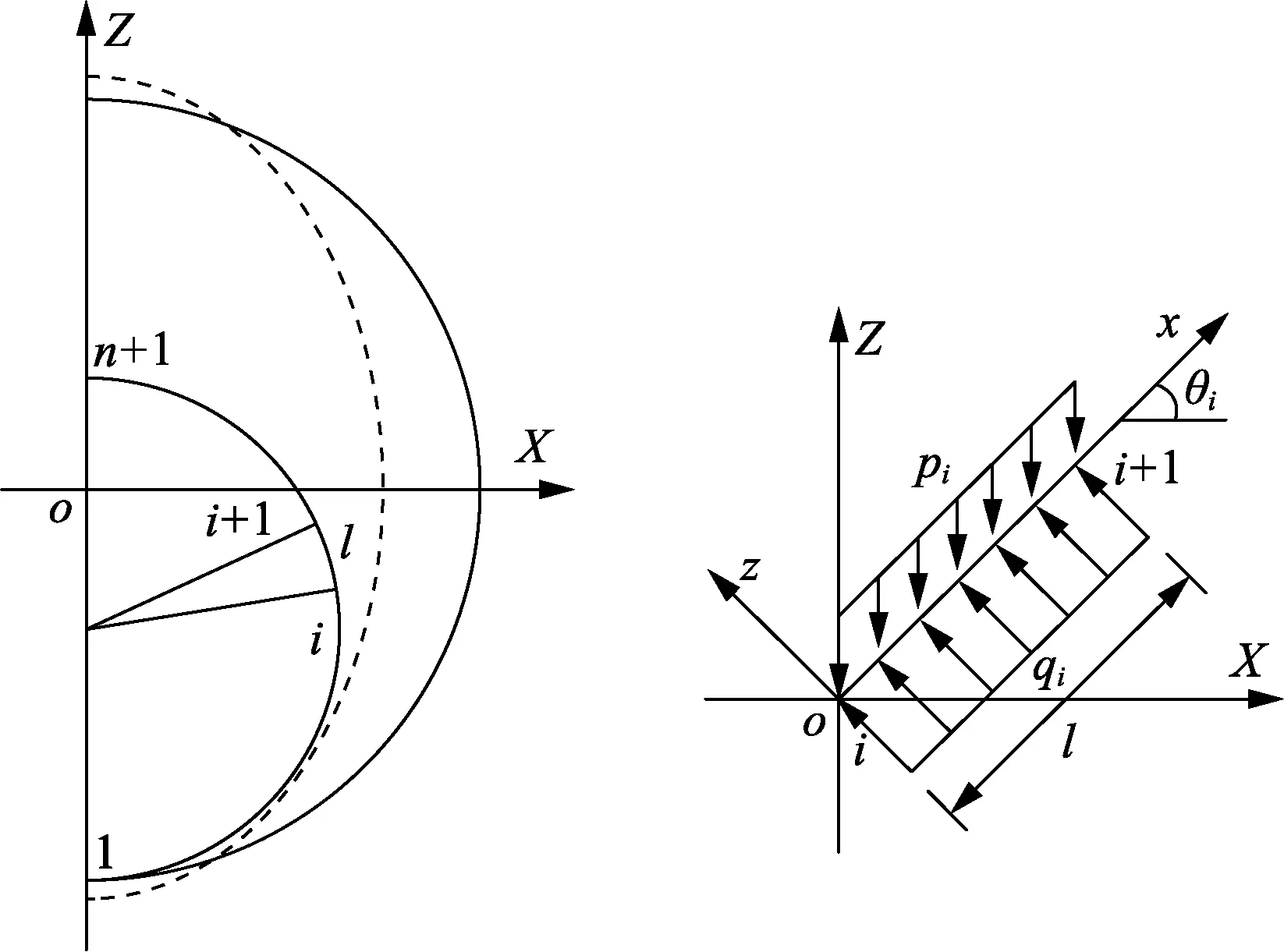
图2 管道单元划分及单元受力简图Fig.2 Element meshing of pipe and mechanics status of element

采用每个结点有3个自由度的2结点平面刚架单元进行分析,结点位移包括单元轴线方向及其垂线方向上的线位移、结点转角,结点载荷包括轴力、剪力与弯矩。分析中的单元可区分为两类,即与地基不接触的单元和与地基接触的单元;对于前者,根据最小势能原理采用变分法可得在单元局部坐标系(图2)下的单元刚度矩阵[K1,e][12],表示为

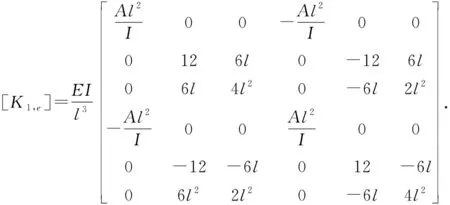
(1)

式中,E为弹性模量,Pa;I为单元的截面惯性矩,m4;l为单元长度,m;A为单元的横截面积,m2。

局部坐标系下单元平衡方程为

[K1,e]{Φe}={Pe}.

(2)

式中,{Φe}为单元的结点位移列阵;{Pe}为单元的等效结点载荷列阵。

由于存在管土耦合作用,单元刚度矩阵[K1,e]不能用于分析与地基接触的单元和推导其单元刚度矩阵。

采用Winkler模型描述地基,单位面积上管道与地基之间的相互作用力为

q(x)=kv(x).

(3)

式中,k为地基反力系数,Pa/m;v(x)为管土接触点处沿管土接触面法向的位移,m。

因管土耦合作用产生的等效结点载荷列阵{Pc,e}为

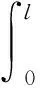
(4)

其中

[N]=[0N2N30N5N6],

N2=(l3-3lx2+2x3)/l3,

N3=(l2x-2lx2+x3)/l2,

N5=(3lx2-2x3)/l3,

N6=-(lx2-x3)/l2.

式中,[N]为形函数矩阵。

单元平衡方程为

[K1,e]{Φe}={Pe}+{Pc,e}.

(5)

将式(4)代入式(5)整理可得

(6)

则与地基接触单元的刚度矩阵为

(7)

1.2 等效结点载荷计算

如图2所示,取第i单元进行分析,记单元局部坐标系x轴与整体坐标系X轴间的夹角为θi。假定单元内管土间作用力为均布载荷qi,大小等于单元中点处的管土作用力,则局部坐标系下单元i的等效结点载荷列阵为

(8)

式中,P为管道承受垂直向下的体积力载荷,N;r为管道半径,m。

单元i不与地基接触时，qi=0；单元i与地基接触时，记管道圆心与单元中点在整体坐标系中的坐标分别为(0,Zp)和(Xm,Zm)，则

(9)

对于圆形地基：

对于椭圆形地基：

1.3 木楔效应求解步骤

(1)对管道划分单元。根据管道圆心的初始坐标计算结点坐标以及各单元局部坐标系x轴与整体坐标系X轴之间的夹角;

(2)假定管道为刚体,根据Z向的静力平衡条件通过迭代运算确定管道圆心的坐标,并判断两种单元的分界点;

(3)生成各单元的刚度矩阵与等效结点载荷列阵,并通过坐标转换[12]合并成整体刚度矩阵与整体等效结点载荷列阵;

(4)根据力的边界条件与位移边界条件修改整体刚度矩阵与整体等效结点载荷列阵;

(5)采用Doolittle分解法求解整体平衡方程,得到结点位移,进而可分析管道位移与管土间作用力。

2 木楔效应变化特性

回拖力预测模型在计算管土摩擦力时,大多直接采用管土间作用力在垂直方向(Z轴)的分力作为管土法向作用力,没有考虑导向孔对管道的夹持作用,低估了管土摩擦力;而管土间作用力在水平方向(X轴)的分力分布于管道两侧,大小相等,方向相反,尽管合力为零,但对管土摩擦力有贡献作用(图3)。管道受力状态与木楔钉入孔中时木楔受力状态相似,该现象称为木楔效应[6]。将管道从与导向孔初始界面相切位置移动至平衡位置时其圆心的位移定义为管道位移,记为wp;对于椭圆形导向孔,wp等于管道从与对应圆形导向孔的相切位置移动至平衡位置发生的位移,如图3(b)所示。定义管土间作用力与其在Z轴上分力的比值为木楔效应系数,记为Kc,将管土间作用力在X、Z轴上的分力分别记为Qx、Qz,则

(10)

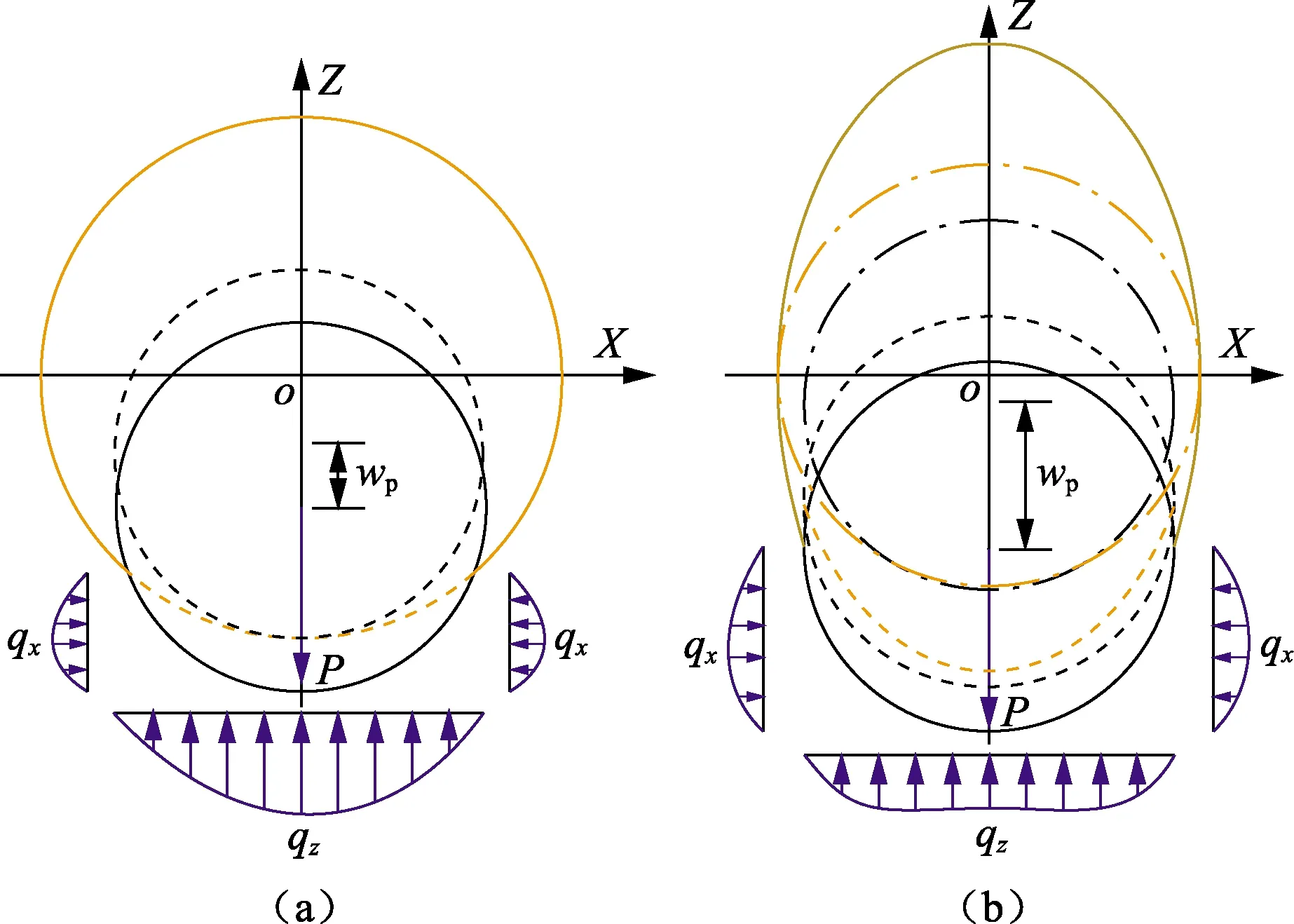
图3 管土耦合作用分析示意图Fig.3 Mechanical analysis of pipe-soil interaction

根据wp修正管道弯曲的挠度,可得管道所受外载荷P,进而计算Kc,用于求解管土摩擦力,据此修正后的管土耦合作用使回拖力预测更符合实际工况。对图1所示两种管土耦合模型进行分析,计算所需初始参数包括管道半径(109.5 mm)、壁厚(12.9 mm)、圆形导向孔半径(150 mm)或椭圆导向孔长/短半径(163 mm/150 mm)、外载荷(1 200 N)、地基反力系数(7.8×106N/m3)、弹性模量(700 MPa),通过变化单项参数研究外载荷P、地基反力系数k、管材弹性模量E、扩径比[8]、椭圆扁率α等因素对Kc、wp的影响规律。

2.1 外载荷P与Kc、wp关系

在回拖力预测模型[6]中,计算摩擦力所用的管土法向作用力仅为管土间作用力在垂直平面内的分力,可视为本文分析中管道承受的外载荷P。考察不同载荷P下木楔效应系数Kc与管道位移wp的变化规律,如图4所示。由图4可见,随着P增大,Kc与wp均呈增大趋势,wp与P呈现较好的线性关系,而Kc的增大速度随P增大趋于平缓。椭圆形地基的Kc、wp始终大于圆形地基的Kc、wp,但Kc的差别较小,在0.001 0～0.005 2内,两种地基的wp之差则维持于约0.020 m。

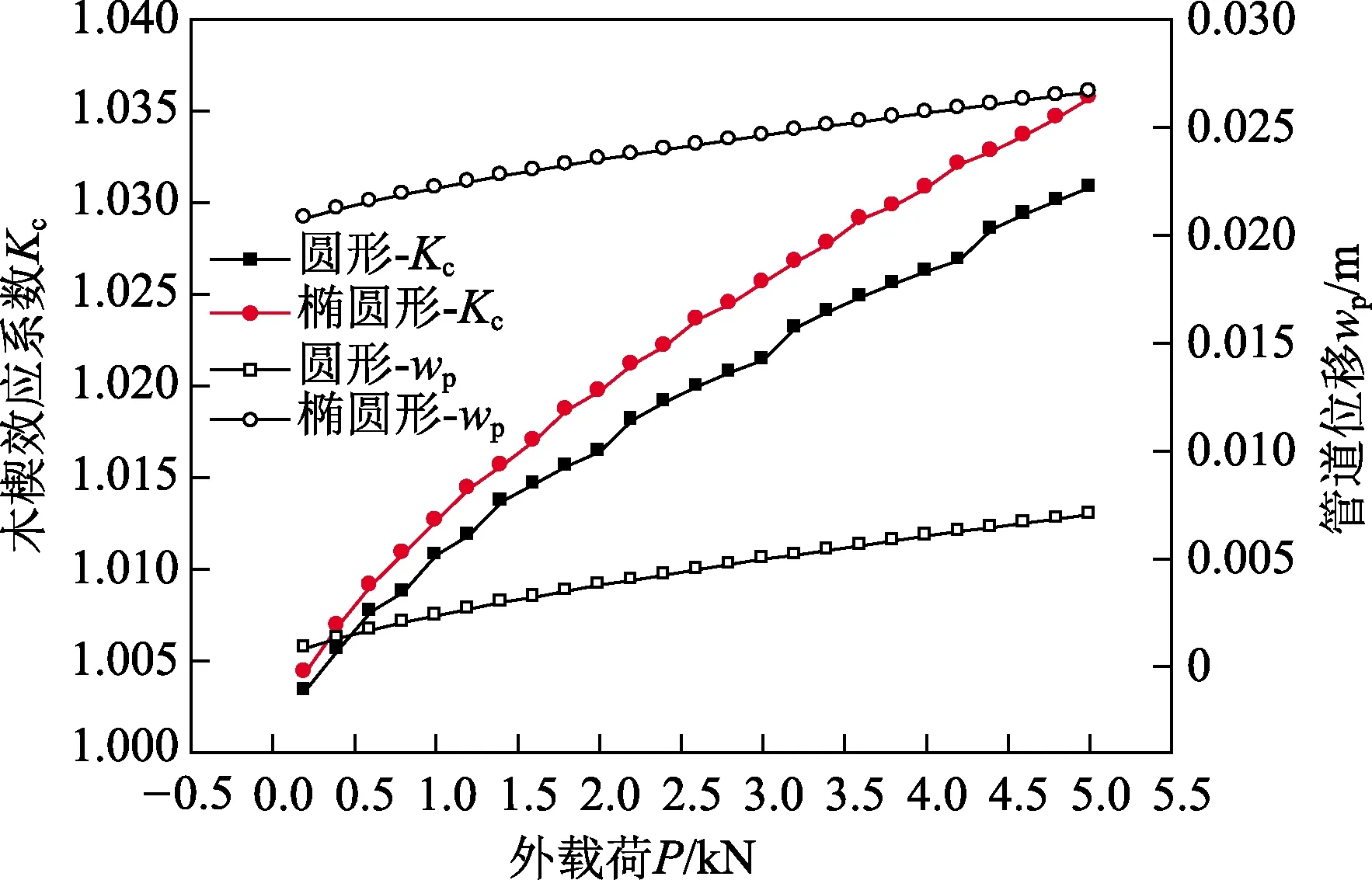
图4 P与Kc、wp关系曲线Fig.4 Influence of P on Kc and wp

2.2 地基反力系数k与Kc、wp关系

地基反力系数受基础几何形状、基础尺寸、土壤类型、上覆土厚度、作用时间等因素影响,呈现复杂的变化规律[13-14],工程中通常采用固结试验或三轴试验进行测定。例如,极软黏土、硬黏土与浸水砂的地基反力系数典型值依次为1.56×106、7.80×106和2.50×107N/m3[15]。选定范围2.0×106～ 2.6×107N/m3考察k对Kc、wp的影响,如图5所示。

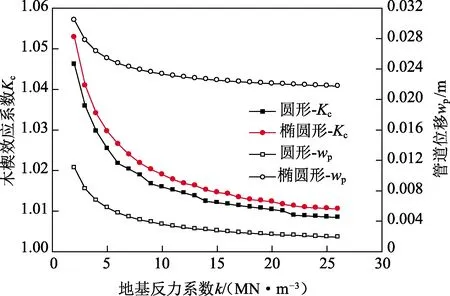
图5 k与Kc、wp关系曲线Fig.5 Influence of k on Kc and wp

由图5可以看出,Kc随k增大呈减小趋势,圆形地基对应的曲线单调递减,但椭圆形地基在k为(1.8～2.2)×107N/m3内出现相反的规律,Kc随k的增大而增大。从图5 中还可看出,椭圆形地基的Kc总大于圆形地基的Kc,两者之差在0.001 6～0.005 1。管道位移随地基反力系数的关系曲线均呈单调递减趋势,且减小速度随k增大趋于平缓。椭圆形地基的wp明显高于圆形地基的wp,两者之差维持于约0.020 m。

2.3 扩径比与Kc、wp关系

导向孔的最终孔径与管道外径之比称为扩径比,扩径比的取值与管道直径、穿越长度及施工队伍的操作水平有关[16],典型值为1.5[17]。图6给出了圆形地基中扩径比与Kc、wp的关系。从图6中可以看出,随着扩径比增大,Kc单调减小,wp单调增大。由于扩径比是水平定向钻穿越中可有效控制的参数,工程中可适当增大扩径比的取值以减小Kc。

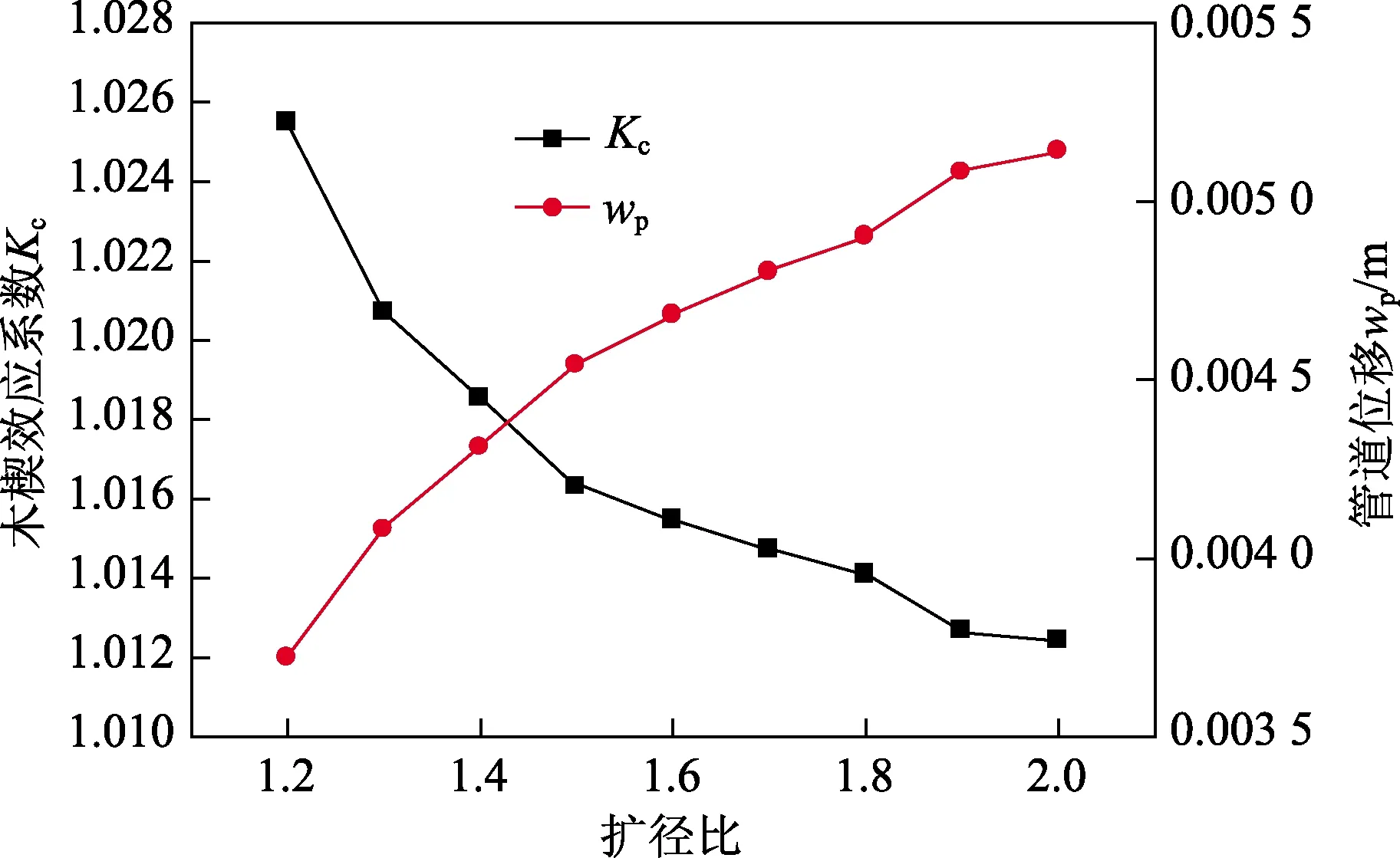
图6 扩径比与Kc、wp关系Fig.6 Influence of expanding diameter ratio on Kc and wp

2.4 椭圆扁率α与Kc、wp关系

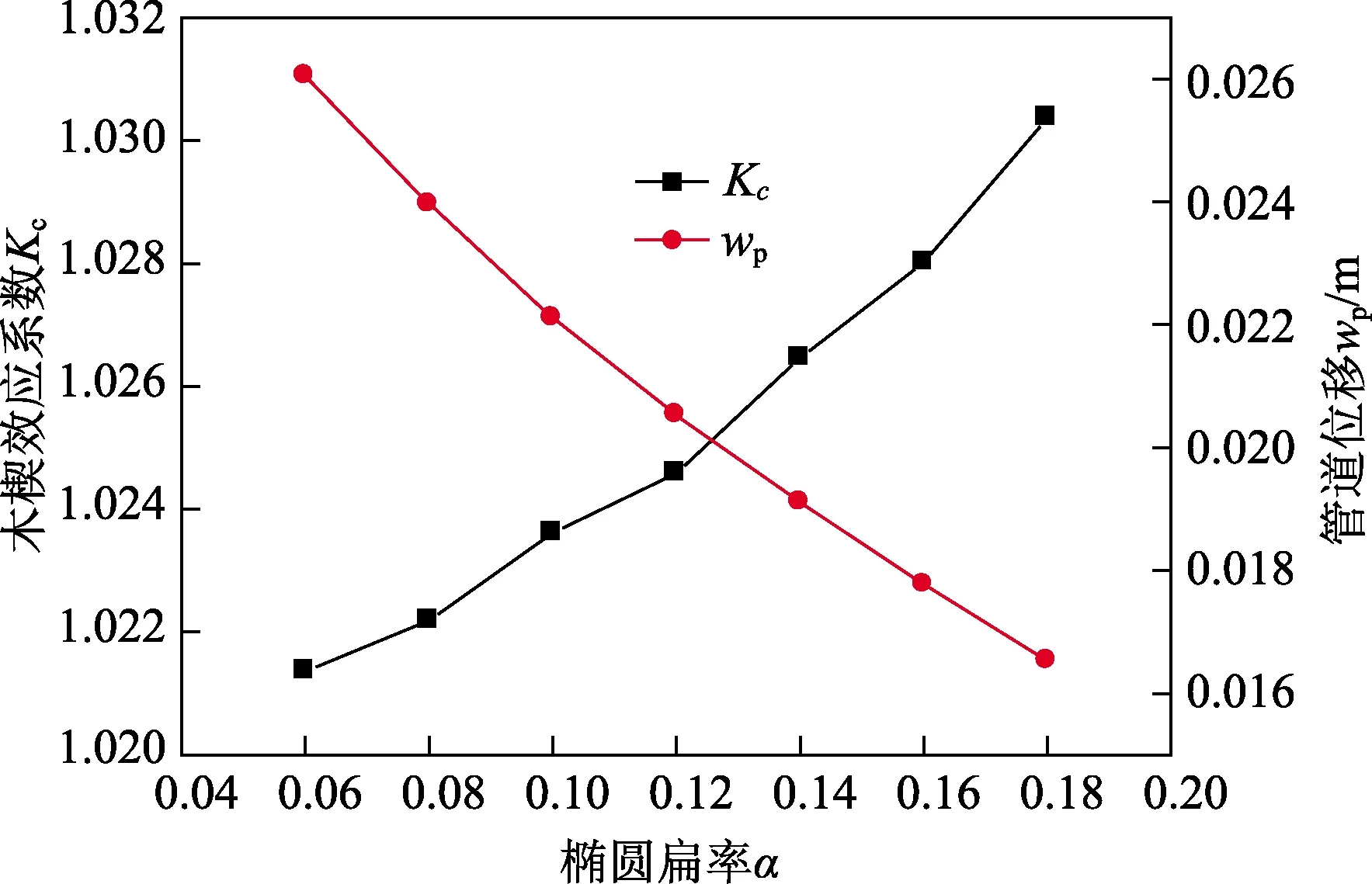
图7 α与Kc、wp关系Fig.7 Influence of α on Kc and wp

椭圆的长、短半径之差与长半径的比值称为椭圆的扁率,记为α。水平定向钻穿越工程中导向孔孔径是固定值,即椭圆短半径a为定值,变动椭圆长半径b考察α对Kc、wp的影响,如图7所示。由图7可见,当α增大时,Kc单调增大,wp单调减小,且Kc的增大速度随α增大而增加。回拖力分析中,wp减小时弯曲梁的挠度增大,所得外载荷P也增大,wp减小亦会增大Kc。这表明椭圆扁率α可迅速增大回拖力,工程中应采取措施减小椭圆扁率α,甚至避免椭圆形地基的出现。

3 木楔效应在回拖力预测中应用

3.1 木楔效应系数在回拖力预测模型中应用

水平定向钻回拖力预测模型[6]将回拖阻力拆分为4项分力,其中3项分力的计算需考虑木楔效应,包括孔内管道自重及其引起的摩擦力、导向孔方向改变引起的摩擦力、孔内钻柱承受的阻力,计算公式分别为:

(1)孔内管道自重及其引起的摩擦力[6]。

(11)

(2)导向孔方向改变引起的摩擦力。

F1=TKi(eμb-iKc-iγs-s-i-1),

(12)

F2=Kc-iμb-iPi+Kc-iμb-iPs-i-1+Kc-iμb-iPs-i-2.

(13)

(3)孔内钻柱承受的阻力。

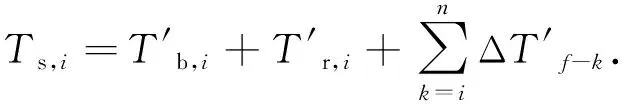
(14)

计算木楔效应系数所需的初始参数中,管道或钻柱的半径r、壁厚δ与弹性模量E以及导向孔半径R可基于穿越工程数据确定;导向孔横截面椭圆扁率α需结合实际工程条件在穿越工程实测数据范围内根据经验确定;地基反力系数k根据穿越点位置处的地层类型进行取值。外载荷P需根据阻力类型进行确定:计算孔内管道自重引起的摩擦力时P为单位长度管道引起的管土法向作用力,计算绞盘力F1时P为计算点Ki处各项阻力之和TKi因绞盘效应引起的管土法向作用力,计算管道弯曲效应所致阻力F2时P为各计算点处因管道弯曲效应引起的管土法向作用力,计算孔内钻柱承受的各项阻力时P的取值方法与上述原则相同。

3.2 实例分析

为考察木楔效应对水平定向钻回拖力预测的影响,采用Cai与Polak[6]建立的回拖力预测方法分别计算钢管、HDPE管两例穿越工程的回拖力。钢管穿越地层中,水平距入土点96 m、距出土点59 m内两段均为淤泥质粉质黏土层(计算点1、17),中间段为粉细砂层(计算点2～16);HDPE管穿越地层除入土点与出土点附近小范围地段为黏土层外,均为砂层(计算点1～16);计算中采用极软黏土、浸水砂的地基反力系数。穿越曲线结构根据导向孔钻进阶段的定位数据确定(图8),回拖力计算所需的工程数据如表1所示。两例穿越工程的回拖力实测值、预测值以及忽略木楔效应的预测值如图9所示。

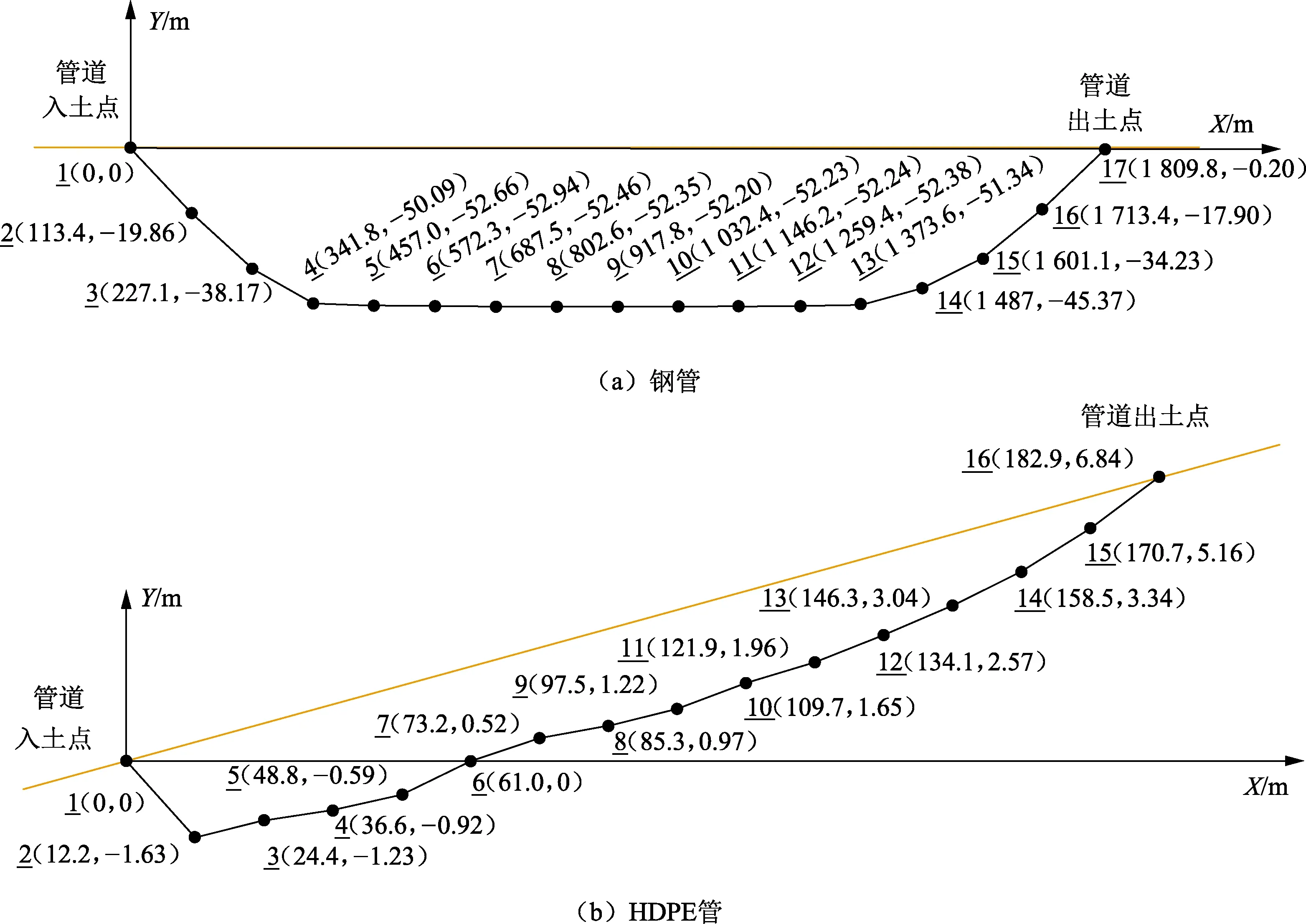
图8 工程测定的穿越曲线结构Fig.8 Measured pilotbore profile on situ

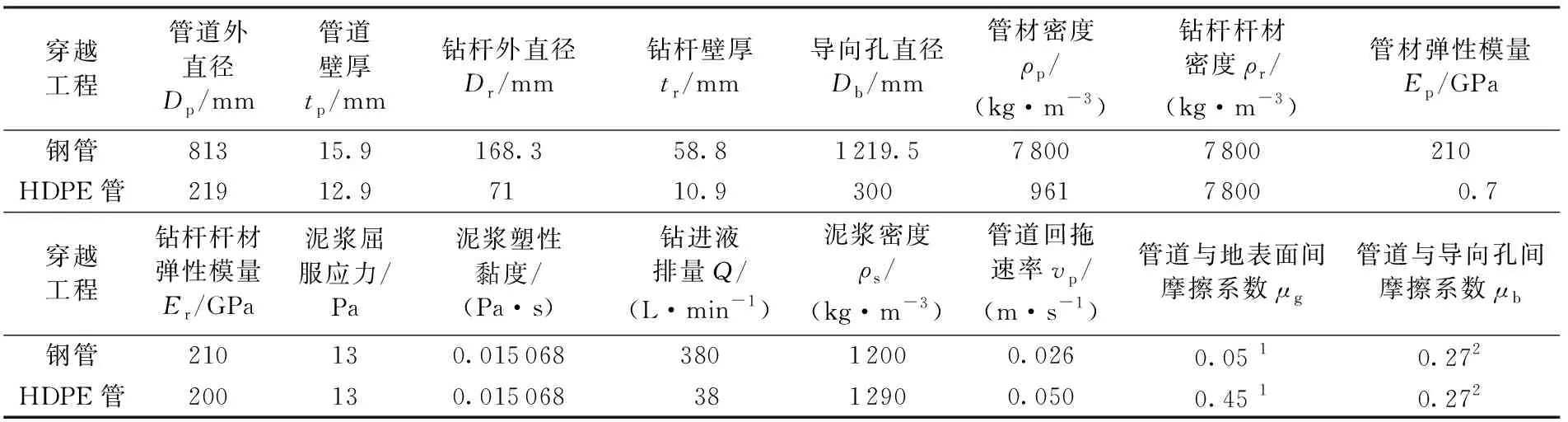
表1 回拖力预测分析所需参数

注:1. 钢管回拖时采用了注水发送沟减阻技术,管地间摩擦力大幅降低;HDPE管回拖时置于草地上,且管道与导向孔的轴线有偏角。

2. 管孔摩擦系数采用EI-Chazli等[18]的实验测定数据。

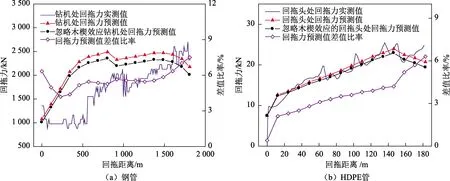
图9 木楔效应对回拖力预测影响Fig.9 Influence of wedging effect on pulling forces prediction

图9中,差值比率为两个回拖力预测值之差与考虑了木楔效应的预测值之比。由图9可以看出,在钢管穿越工程中,回拖点1、9～17处回拖力预测值与实测值有较好的一致性,回拖点2～8处回拖力预测值显著高于实测值。其原因是在回拖距离60 m后,泥浆中使用了润滑添加剂,令管道与导向孔之间的摩擦系数减小,而泥浆在反向点(约1 000 m处)后由钻柱一侧返回地面,管道与导向孔之间缺乏含润滑剂泥浆的有效补充,摩擦系数又恢复正常值;当不考虑木楔效应时,回拖力预测值下降4.3%～7.7%。在HDPE穿越工程中,回拖力预测值与实测值有较好的一致性,回拖力预测最大值23.97 kN出现于146.3 m处,而工程实际数据分别为25.44 kN、135.9 m;当不考虑木楔效应时,回拖力预测值下降0.4%～6.3%。需要注意的是,HDPE管穿越工程的差值比率随回拖距离由小变大,呈单调变化趋势,不同于钢管穿越工程。其原因为HDPE管、钢管穿越的回拖力实测值分别为回拖头处回拖力、钻机处回拖力,钻机处回拖力包含了孔内钻柱承受的阻力,而这部分阻力同样存在木楔效应现象。

4 结 论

(1)HDD回拖过程中导向孔对管道有夹持作用,管土间作用力在水平方向上存在一对大小相等、方向相反的分力,尽管合力为零,但对管土间摩擦力有贡献作用。

(2)当外载荷、椭圆扁率增大,地基反力系数、扩径比减小时木楔效应系数均增大;当外载荷、扩径比增大,地基反力系数、椭圆扁率减小时管道位移均增大。

(3)木楔效应对回拖力预测有显著影响,导致预测值减小幅度可达7.7%,在回拖力预测中不可忽略。