全轴转向双铰接车辆的轨迹跟随优化分析

周 胜，张陈林，周承明，钟汉文

（中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

随着经济的快速发展，交通拥堵问题已成为困扰城市居民出行的主要问题之一，严重制约了居民的出行和商业运输效率。铰接式车辆由于运载量大，成为解决城市道路拥堵问题以及长途货物运输的主要方案，但双铰接式汽车由于编组过长，车辆在弯道行进时会出现车道占用宽度大、转向灵活性较差等问题，限制了双铰接车辆的发展，也对车辆结构设计提出了更高的要求。车辆铰接连接方式由于连接简单、操作灵活，是一种较为普遍的车辆连接方式，国内外学者对其进行了大量的研究[1-3]。以往的研究主要集中在铰接运载货车上，由于其运行工况均为高速公路和空旷区域，所以这些研究仅关注车辆的操作性能，而不考虑车辆本身的转向灵活性与道路占用情况；另一方面，全轴转向技术的发展给长编组列车提供了全新的解决方案，可以利用车辆部分或者全部车轮的转向提高整车运行时的可靠性，减小车辆的跟随误差[4-6]。可见，目前对于双铰接车辆研究较少，且已有的研究主要集中于铰接车辆的动力学性能与自动驾驶轨迹优化，较少考虑长编组车辆转向时道路占用问题，无法很好地满足双铰接长编组车辆的设计需求[7-10]。为了解决双铰接车辆的前后轴轨迹偏移问题，本文以中车株洲电力机车研究所有限公司（简称“中车株洲所”）研制的智轨电车为基础，利用双铰接全轴转向车辆的运动学模型和弯道运行时的转向跟随模型开展研究，完成了一阶延时转向条件下车辆的轨迹跟随分析，建立了一阶延时参数计算的经验公式，并通过仿真分析验证了本文所提优化方法的有效性。

1 双铰接车辆的运动方程

通常情况下，车辆运行道路情况非常复杂，整车自由度较多。为了简化车辆的运行模型，本文在计算过程中忽略了道路竖向坡度，且不考虑横坡对跟随性能的影响。车辆正常行驶时，车身的平面运动是影响车辆通行所占用道路宽度的主要因素，所以在研究车辆运行过程中占用道路宽度时，可以忽略车辆的垂向运动，仅考虑水平面内车辆的运动过程。根据Ackermann 转向模型，带两轮的车桥结构可以被简化为中心轮模型进行分析。忽略车桥梯形转向机构对车身运动的影响，铰接车辆可以采用简化的中心轮模型进行运动学分析。本文采用智轨电车作为分析对象，车辆的结构形式如图1 所示。其中，li0为第i 节车厢前轴距车头（中间车为车厢前部铰接盘中心点）的距离，li1为第i 节车厢前轴距当前车厢质心的距离，li2为第i 节车厢后轴距当前车厢质心的距离，li3为第i 节车厢后轴距车尾（中间车为车厢后部铰接盘中心点）的距离。

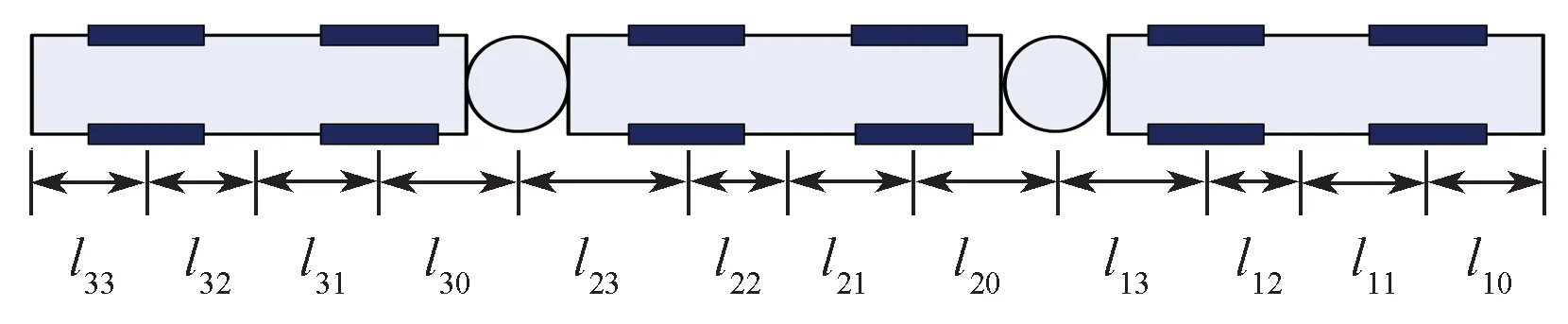
图1 全轴转向双铰接车辆的结构Fig. 1 Structure of a double-articulated vehicle with full-axles steering

智轨电车为三编组双铰接车辆，车厢之间采用铰接盘连接方式，可绕中心轴承平面内旋转。为了增加车辆的承载能力与运行时的稳定性，车辆采用6 个车轴的架构形式，即每节车厢均有两根车轴。根据图2 所示的双铰接车辆的运动模型，建立智轨电车的运动学方程。图中δi为第i 个车轮的转角，v1为第1 个车轮速度。

图2 双铰接车辆的运动模型Fig. 2 Kinematic model for a double-articulated vehicle

建立如图2 所示的固定坐标系XOY，相比车厢之间绕铰接盘的转动，由于车体的变形量较小，对道路通过性的影响可忽略不计，所以车辆底盘与车身结构可简化为刚体，仅需要考虑车身的平动与转动，即单节车厢的平面上的姿态可由3 个坐标定义，记为坐标Qi=[Ri, θi]T。其中，Ri为第i 节车厢的质心坐标向量，在固定坐标系中可表示为Ri=[xi, yi]T；θi为第i 节车厢的航向角，即车身与x 轴的夹角；φi为第i 节车厢和(i+1)节车厢之间的夹角，夹角方向以顺时针方向为负、逆时针方向为正。由于3 节车厢之间采用铰接方式连接，可以推导出铰接点处坐标的约束方程如下：

其中，Λi=[cosθi, sinθi]T。

由于Rn可以根据R1以及θi计算得到，所以表示三编组铰接车辆的姿态广义坐标可以缩减至4 个，用符号q=[R1, θ1, θ2, θ3]T表示。

根据运动学方程，利用车轮角度以及各车轮速度可以计算任意时刻整车的广义速度。

式中：vi——第i 个车轮的速度；ω1——第一节车的横摆角速度。

同理，可以根据车身姿态计算两个车厢之间的铰接角：

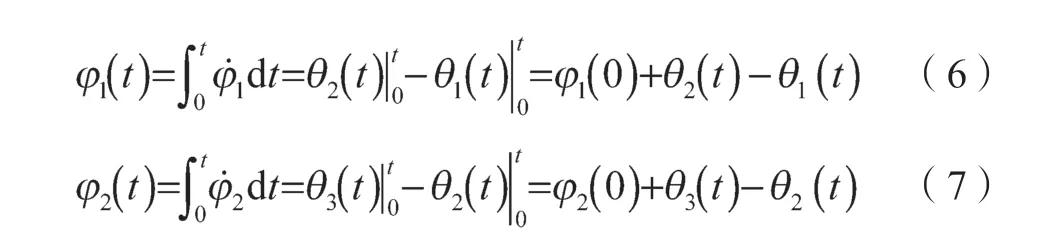
2 双铰接车辆的轨迹跟随算法

非全轴转向车辆转弯时，由于后轮与车身角度始终不变，车厢的旋转中心为后轴，即后轴的运动方向与车身保持一致，导致前后轮轨迹差的出现，增加了整车运动时占用路面的宽度。双铰接车辆由于整车车身较长，如果各轴跟随性能较差，后面车辆会放大占用道路宽度，对车辆运营造成极大的影响甚至威胁旁边车辆与行人的安全。

通常，车辆从直线进入弯道运行时分为两个阶段，即弯道进入阶段以及稳态转向阶段。弯道进入阶段为车辆从直线进入弯道且整车未完全进入弯道之前的时段；弯道稳态转向阶段为车辆完全进入弯道中、前后轮进入固定半径弯道的转向阶段。

在弯道进入阶段，为了缩小车辆运行过程中占用路面宽度，需要确保两节车厢车轮运行的轨迹与道路方向一致。本节以单节车厢为研究对象，分析车辆转弯过程中的跟随性能，然后推广至3 节车辆的结构。图3 示出不同转向策略下车辆的运行姿态，可以看出，车辆后轮不转向时会出现向弯道内侧运行的现象，车身姿态可以利用运动学方程计算，用Qi=[Ri, θi]T表示；通过调整车辆的转向（一般情况下与前轴方向相反）能够改变车辆的运行轨迹，车身姿态则变为Q′1=[R′1, θ′1]T。为使转向阶段轨迹偏差最小，车轮轨迹需要在两个阶段分段满足轨迹要求，在弯道进入阶段时，后轮的轨迹与直线重合，则

yw2(t)=0 （8）式中：yw2(t)——车辆第二个车轮的运动轨迹。

根据运动学方程计算可得

式中：v2——第二个车轮的速度；v2y——v2在y 方向的分量。

根据式（9）可以推导出

图3 不同转向情况下弯道运行的车辆姿态Fig. 3 Attitudes of the vehicle operating in curves in different steering conditions

当车辆处于稳态转向阶段时，根据Ackermann 转向定理，车辆绕一固定圆心做圆周运动；理想转向时，前轮与后轮在同一圆周上，此时前轮与后轮转向角度大小相等，方向相反，即：

根据车辆的运动过程以及智轨电车的设计要求，转向过程中，各轴的转角为小量，即。可以简化方程，令 tanδi≈δi，cosδi≈1，改写式（11）为差分方程，构建轴2 转角求解的迭代格式：

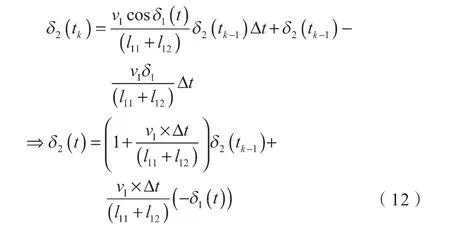
式中：δ2(t)——t 时刻δ2的值；δ1(t)——t 时刻δ1的值； δ2(tk)——t=kΔt 时δ2的值；Δt——车辆转向的最小控制时间间隔。

根据运动学方程可以离散化车辆的运行轨迹，编程计算得到前轮与后轮的轨迹（图4）。利用已知路径和车辆的实时姿态，计算车辆从开始入弯到完全进入弯道的分界时间T：当t ≤T 时，轴2 的转角满足式(10)； t＞T 时，轴2 的转角满足式(11)。从图4 中可以看出，当后轮与前轮之间的关系满足上述的转向状态时，后轮运行轨迹与前轮重合。

图4 全轴转向时的理想轨迹Fig. 4 Ideal path of the front and rear wheels in all-wheel steering condition

虽然利用式(10)和式(11)可以得到车辆理想的跟随曲线，但是由于转向是一个按路径的分段过程，需要准确地识别图3 中弯道进入阶段与稳态转向阶段的分界线，即分界时间T。实际车辆运行时，由于不知道车道状态，对T 进行计算非常困难，需要采用相似函数对车辆后轮转角进行拟合，以避免车辆运行时转向角度与路面位置相关。对式(13)进行Z 变换，可得

对式（14）取Z逆变换，可以求出时域内的δ2表达式：

从式 （15）可知，由于m1＞1，mk1 在无穷远处不收敛；随着时间增加，δ2会一直增加，不符合真实车辆转弯时的运行规律。综合式（10）与式（11）的条件，利用一阶延时函数拟合后轮的变化规律，逼近δ2理想转角。修改 m1的值，令m1=1-m2，则可以得到修正后的一阶延时转角方程，计算得到时域中δ2(t)的表达式：

随 着 时 间 变 长， 由 式（16） 可 以 计 算 得 到δ2(+∞)=-δ1，满足弯道内稳态运行的前后轴的转向条件。图5 示出采用修正后的一阶延时函数时，实际转角与理想转角的变化趋势。可以看出，利用修正参数后的一阶延时函数，实际转角与理想转角变化趋势较为接近。

图5 实际转角与理想转角的变化趋势Fig. 5 Variation trend of actual and ideal steering angles

虽然一阶延时函数与理想转向函数有一定的差距，无法满足入弯过程中的精确跟随，但通过调整一阶延时函数的参数可以改变前后轮轨迹偏差，通过调整车辆限界大小可以提高跟随精度。图6示出m1取不同值时前轮与后轮的轨迹图。可以看出，利用一阶延时函数转向近似代替车辆理想转向过程，会产生跟随误差。优化m1的大小，可以减小后轴与前轴轨迹的跟随误差，提高车辆的跟随精度。

图6 m1 变化时前后轮轨迹变化Fig. 6 Trajectories of front and rear wheels with m1 changing

3 主动转向的优化方法

根据第一列车主动转向的研究方法，可以扩展到3 列车的前后车轮的跟随方式。利用前后两个铰接点的延时跟随方式，根据式（2）～式（5）所示的车辆姿态计算过程，可以得到车辆任意时刻的姿态信息q(x1, y1, θ1, θ2,θ3)，进而求出不同时刻智轨电车的姿态以及各车轴与固定路线的横向偏差，如图7所示。

图7 双铰接车辆转弯轨迹偏差图Fig. 7 Schematic diagram of steering trajectory deviation of double-articulated vehicle

由图7 可知，双铰接车辆进入弯道过程中，车辆运行姿态对限界会产生影响，最大影响处为车辆的3 个铰接点（第3 个铰接点为车尾虚拟铰接点）。车辆运行过程中，直线区域的轨迹偏差为e1+与e1-（其中下标“＋”和“-”分别代表“正向偏差”和“负向偏差”），曲线区域的轨迹偏差为e2+与e2-。根据式（2）～式（5），可以求出3 个铰接点随时间的位置变化，分别记为(S1x, S1y)、(S2x, S2y)和(S3x, S3y)，各偏移量可以表示为

当车辆运行时的轨迹偏差最小时，路面占用宽度最小。根据式（17）的轨迹偏移量的计算方法，可以得到轨迹偏差优化目标函数和条件：

编程实现双铰接车辆3 节车厢运行轨迹偏差函数优化，最终可以求出不同速度条件下车辆的轨迹偏差最小时m1的值。利用车辆计算结果，可以求出车辆不同速度条件下的最优参数与车速之间的关系。利用函数拟合，可以得到延时函数参数与速度为线性关系：

式中：ai——线性函数系数，可以通过优化计算得到a1=0.275，a2=0.217，a3=0.260。

图8 示出采用一阶延时转向与非全轴转向的智轨电车在进入半径为20 m 弯道时，两个铰接点以及车辆尾部的轨迹跟随图。可以看出，利用最优化一阶延时函数转角方程计算得到的全轴转向方法运行的多编组双铰接车辆车身铰接点的跟随效果优于非全轴转向双铰接车辆。后轴不转向时，由于单节车厢较长，双铰接车辆最大轨迹偏差为3.5 m；采用轨迹跟随一阶延时算法后，最大轨迹偏差仅为0.8 m，后者跟随误差仅为前者的23%。可见，利用优化后的一阶延时转向能够极大减小各车厢之间的跟随误差，提高跟随精度，减小双铰接车辆在正常运营时的道路占用宽度。

图8 一阶延时转向与非全轴转向条件下的跟随效果对比Fig. 8 Following performance comparison between first-order delay steering and non-full-axle steering

4 结语

本文以智轨电车为原型，建立了全轴转向双铰接车辆的运动方程，利用轨迹跟随的优化方法与一阶延时转向方程，进行了延时转向参数的求解。结果表明，利用最优化理论求解的一阶延时转向方法能够有效地提高双铰接车辆的跟随精度，跟随误差仅为不转向铰接车辆的23%，能够大幅度减小正常运营时的道路占用宽度，节约道路建设成本，增加了双铰接车辆运营的可行性并提高了配套基础设施建设的经济性。

本研究中对双铰接车辆的运动模式以及线路情况进行了一定的简化，后续将进一步研究带缓和曲线路线的影响以及不同延时方法的可靠性。