大型直驱风电机组风剪切效应ANN 软测量方法

李志勇，王 欣，王 靛，黄国航

（1.中南大学 自动化学院，湖南 长沙 410075；2.中车株洲电力机车研究所有限公司，湖南 株洲 412001）

0 引言

近年来，国家努力建设环境友好型社会，大力发展清洁能源，尤其是风力发电。为提高效益，风力发电机组逐渐趋于大型化，尺寸逐渐增加；然而由于风速随垂直高度变化而变化，叶片在旋转过程中受力不均，致使风电机组输出转矩产生周期性波动，即风剪切效应[1]，叶片尺寸越大，风剪切效应越严重。目前风电机组设计都采用风轮中心处的风速作为单一的设计风速，这对直径小的风机而言是可行的；而对于大型风电机组，就有必要考虑风速在垂直方向上的变化问题，因为其所受风速的不均匀度更大，输出转矩波动情况更严重。风剪切效应产生的周期性转矩波动，一方面会使叶片拍打振动、塔架谐振，加快部件的损耗，影响风电机组的使用寿命；另一方面，转矩波动会经发电机由机械侧传递到电磁侧，且随着大规模的风电机组并网，含有纹波的电能会大量涌入电网，势必会导致电压波动和闪变等电能质量指标超出国家相关标准要求，严重影响电力系统的安全稳定运行[2]。解决这些问题，首先要精准量化因风剪切效应输出的转矩波动，提供数据和技术支撑对其进行补偿和控制。文献[3]通过现场实测数据证明了10～100 m 高度层，风速随高度的增加迅速增大；而100 m 以上高度层，风速随高度的增加总体呈缓慢增大趋势。风电机组风轮直径达100 m，风速在整个风轮扫掠面上是变化的——每个叶片上的微元方位角相同，在叶片的展开方向上空间位置相差会很大，所受风速相差很大，从而导致3 个桨叶所受气动载荷随方位角呈周期性变化，且如果风轮旋转频率为基准频率，则风电机组气动载荷频率为叶片数的倍频[4]。文献[5]以三桨叶为例分析了这种3 倍频脉动由风电机组机械侧传递至电磁侧的过程，输出功率含3 倍频波动。目前检测风电机组的输出转矩常用的方法是用应变法测轴系转矩[6]，即将应变片粘贴在转轴表面采集数据并分析，这种方法虽然便于应用但易受干扰且精度不高。文献[7-8]运用小波分析和傅里叶分析方法检测谐波，所使用的滤波器难以实现大功率滤波及检测，且检测过程存在延时，不符合实时性要求。

本文以直驱永磁同步发电机为研究对象，基于GH Bladed 软件搭建三桨叶含风剪切风速模型的直驱永磁同步风力发电机组的并网模型，运用基于自适应噪声对消原理的人工神经网络（artificial neural network, ANN），对从机械侧到电磁侧各环节的3 倍频波动进行实时测量，利用转速波动和定子电流纹波间接测量风剪切造成的3 倍频输出转矩波动，软测量风剪切效应。这种方法不需要增加额外的设备，应用灵活，有效解决了无法精确测量输出转矩波动的技术难题。

1 风剪切效应产生机理

风速在垂直高度上的变化规律普遍用指数函数来描述[9]。令轮毂高度H 处的风速V0为参考风速，任一高度h 处的风速V(h)以风剪切系数α 为指数，根据动量-叶素理论[10]，风剪切下某个单叶片所受等效风速模型为式中：W(r, θ)——风剪切函数；r ——桨叶叶素到转轴中点的径向距离；θ ——旋转方位角。

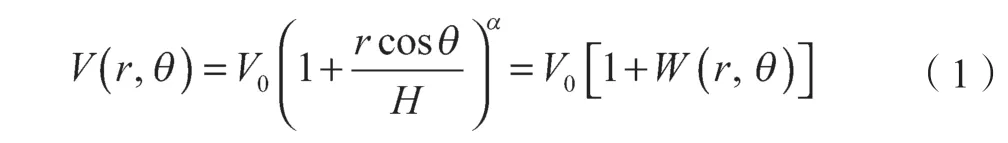
风机部分参数示意如图1 所示。将W(r, θ)项进行三阶泰勒展开，见式（2），其中的cos2θ 和cos3θ 可分解为含有cosθ，cos 2θ 和cos 3θ 的多项式。

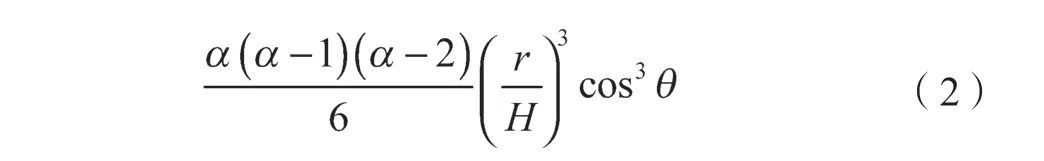
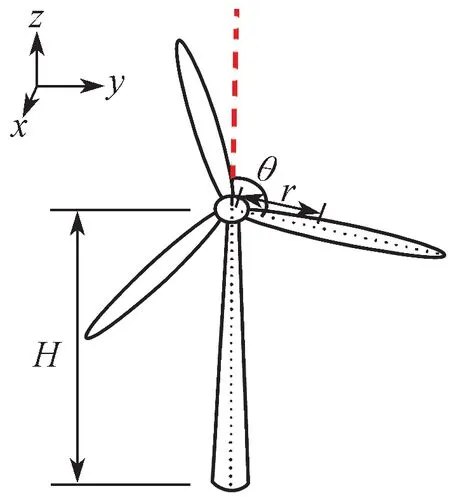
图1 风机部分参数示意Fig. 1 Schematic diagram of some wind turbine parameters

风轮旋转时，等效的风轮输出转矩如式（3）所示：

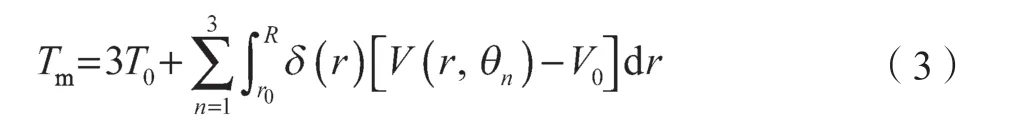
式中：T0——平均风速V0在桨叶根部产生的稳态转矩；r0——叶根部到转轴中点的径向距离；R——叶尖到转轴中点的径向距离；δ(r)——桨叶叶素到转轴中心的距离为r 时，气动负载的影响系数；n ——桨叶数量。

水平轴三桨叶风电机组运行时，3 个对称桨叶的风剪切效应叠加，会导致风剪切效应等效风速中的cosθ项为0；cos2θ 项是直流偏移量；而cos3θ 项则是波动量，且α 越大，波动量越大[11]，风电机组输出含3 倍频的转矩波动。本文设置R=30 m，H=70 m，α=0.3 进行模拟，如图2 所示，风电机组运行时，风速的垂直变化会造成输出转矩的周期性波动，即风剪切效应，波动频率为风轮转速基准频率的3 倍。

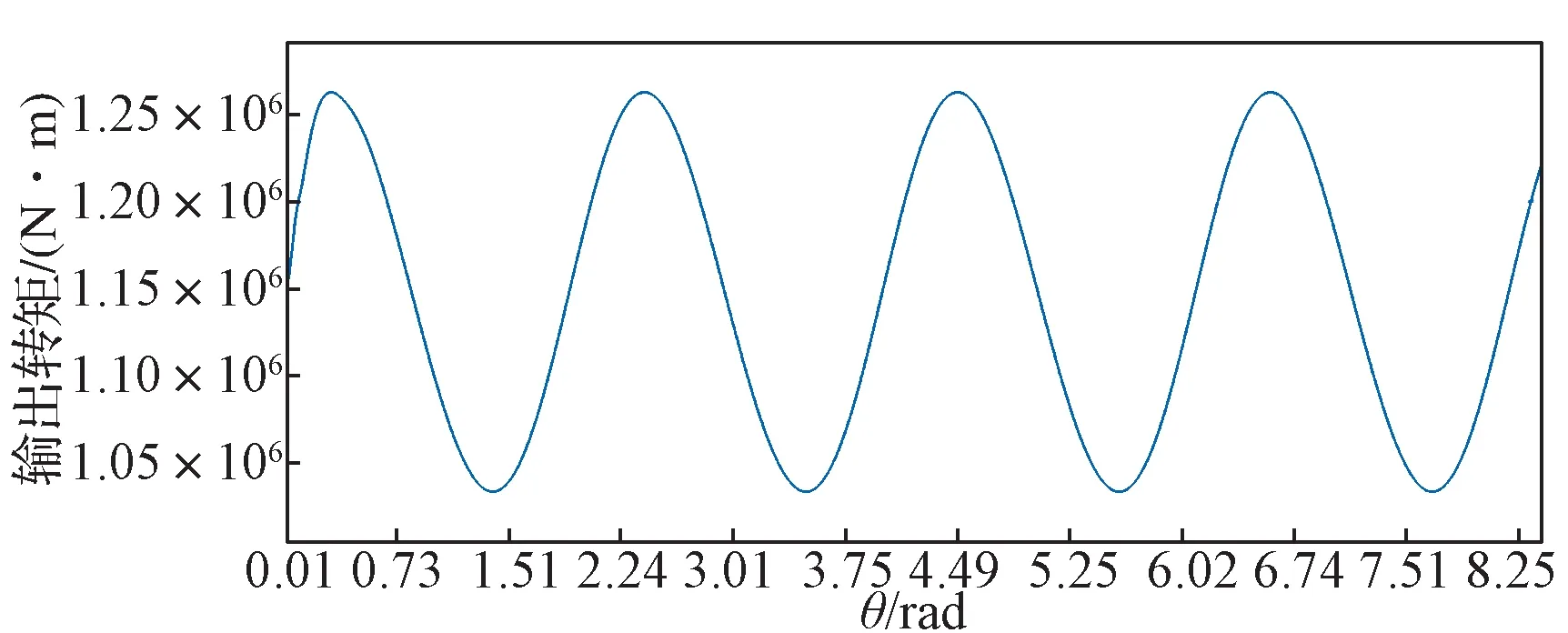
图2 受风剪切影响风电机组的输出转矩Fig. 2 Output torque of wind turbine affected by wind shear

2 风剪切效应下波动传递机理

风剪切效应引起的3 倍频波动会传递到多个环节，包含发电机转速、双PWM 变流器输入电流、变流器输出电压以及并网电流[5，12]，这与风电机组输出功率的3 倍频波动相吻合。

发电机转速是根据最大功率跟踪理论确定的[13]，其取风轮扫风面的平均风速。不同风速下，风电机组的最大功率点不同，转速亦不同。若直驱永磁同步电机为理想电机[14]，风电机组在平均风速不变的情况下运行时，在某个周期内电磁转矩不变，与持续存在周期性波动的输出转矩产生周期偏差。式（4）表明，为了保持转矩平衡，发电机转速产生周期性的波动，且波动频率与输出转矩波动频率一致，此时输出转矩的波动分量传递到转速环节，转速以额定转速频率为基准频率产生了3 倍频波动。

式中：J——转动惯量；ω——实际转速；Tm——输出转矩；Te——电磁转矩；np——发电机极对数；isq——发电机定子q 轴电流；ψf——永磁体磁链。

风电机组启动后趋于稳定，转速波动分量将经过转速外环传递至机侧变流器电流内环中；同时，由于转速波动具有周期性和持续性，发电机所输出的定子电流同样将持续地发生周期性变化，且纹波频率一致。此时，由风剪切效应所造成的输出转矩波动通过转速环传递至发电机组的电磁侧，式（5）表明，纹波进一步传递到电磁转矩中。直驱型风电机组运行时产生的风剪切效应，即输出转矩波动，通过机侧变流器传递到转速环节和定子q 轴电流中（图3）。图3 中，ωref为参考转速。

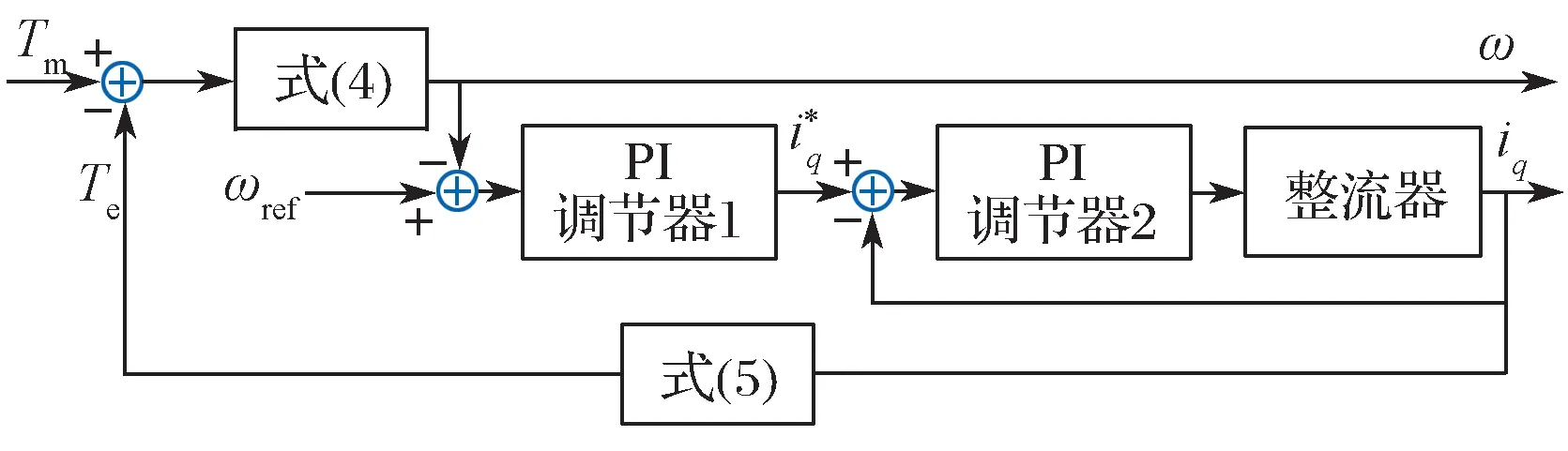
图3 直驱风电机组机侧变流器系统框图Fig. 3 Block diagram of machine-side converter system for direct-drive wind turbine

3 基于ANN 的输出转矩波动软测量

基于ANN 的输出转矩波动软测量以发电机转速传感器和电流传感器采集的信号为基础，通过ANN 信号检测，提取转速和电流中特定频率的波动信号；再经相关的约束计算，观测到输出转矩的波动信号。这种观测方法应用灵活，实时性好，准确度高。

3.1 基于ANN 的信号检测原理

ANN信号检测是基于自适应噪声对消原理[15]（图4），把一个信号从噪声中分离出来。检测系统有两个输入，原始输入（s+n0）和参考输入n′0。s 与n0和n′0分别不相关；n0和n′0相关，为噪声干扰。参考通道的作用就在于检测干扰，并通过自适应滤波器调整其输出n*0，使其在最小方差下最接近n0；同时，n*0与系统输出y 的误差信号e 用于调节自适应滤波器的参数。这种检测方法只需要了解被测信号的频率特征，不需要其他先验数据就可以实现在线实时检测。

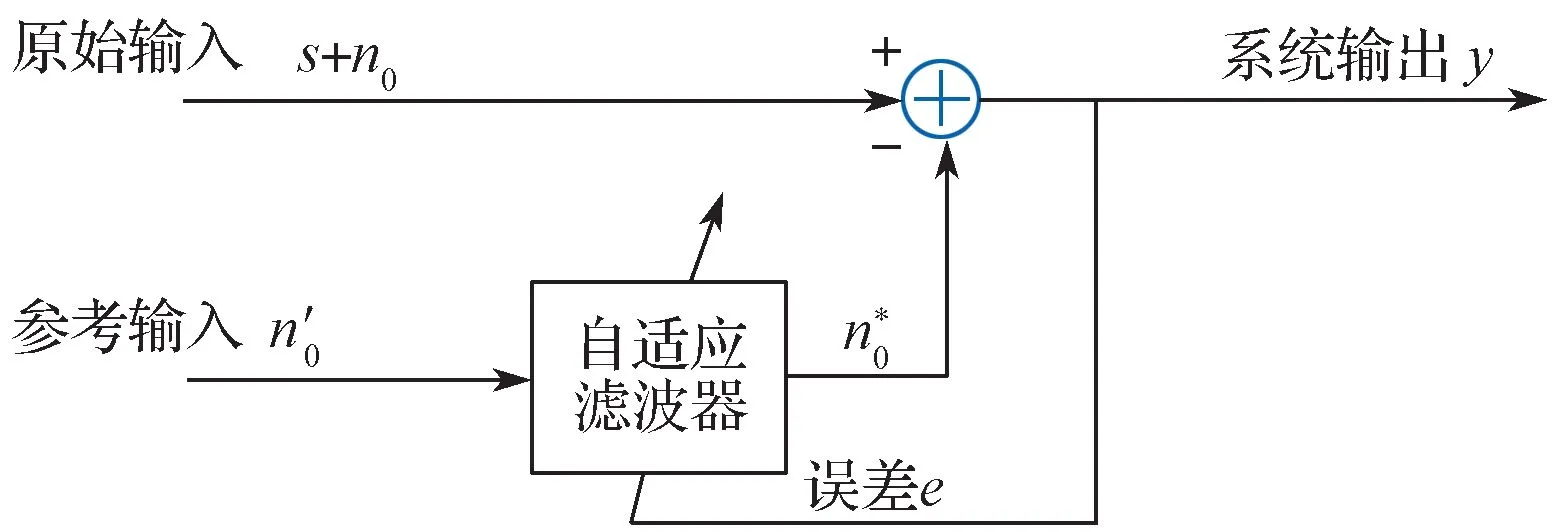
图4 自适应对消法原理图Fig. 4 Principle diagram of adaptive cancellation

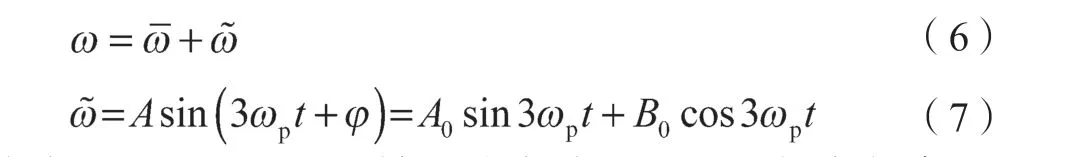
已知风电机组转速波动频率是基准频率的3 倍，即额定转速频率的3 倍。把转速分解为稳定分量和波动分量，表示为式中：——发电机转速稳定分量，也是额定频率；——发电机转速波动分量；ωp——风电机组额定转速频率；φ——转速波动相位角；A0——转速波动正弦分量幅值；B0——转速波动余弦分量幅值；A——转速波动幅值，

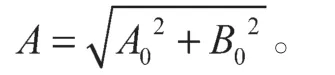
基于式（7）的分解，利用自适应噪声对消原理对转速波动分量进行检测和提取。取ω 作为原始输入信号，作为“噪声干扰”信号，也作为需要检测的信号；取频率为3ωp的正弦、余弦信号作为参考输入，其与“噪声干扰”信号 的正弦和余弦分量有关。经过自适应滤波器在线学习，得到“噪声干扰”信号的正弦、余弦分量在最小均方误差下的最优逼近值。

图4中的自适应滤波器实际上就是利用ANN实现的。基于最大功率点跟踪控制下的风电机组额定转速信号，通过锁相电路PLL，得到正弦和余弦信号sin ωpt 和cos ωpt；再倍频得到3 倍频正弦和余弦信号，将其作为ANN 的参考输入，输入和输出之间的映射关系比较简单，ANN的输出又可由参考输入线性组合而成。考虑到实际操作的可实现性并为提高检测速度，ANN 的结构应该尽可能简单，而单个神经元正好符合这一特点，且具有一定的映射能力和自适应学习特性。基于此，设计了由单个神经元组成的自适应滤波检测电路，其结构原理如图5所示。图中，参考输入是sin 3ωpt 和cos 3ωpt；输出为wssin 3ωpt 和wccos 3ωpt，分别是逼近的正弦和余弦分量，其中ws和wc分别是对应的权值。

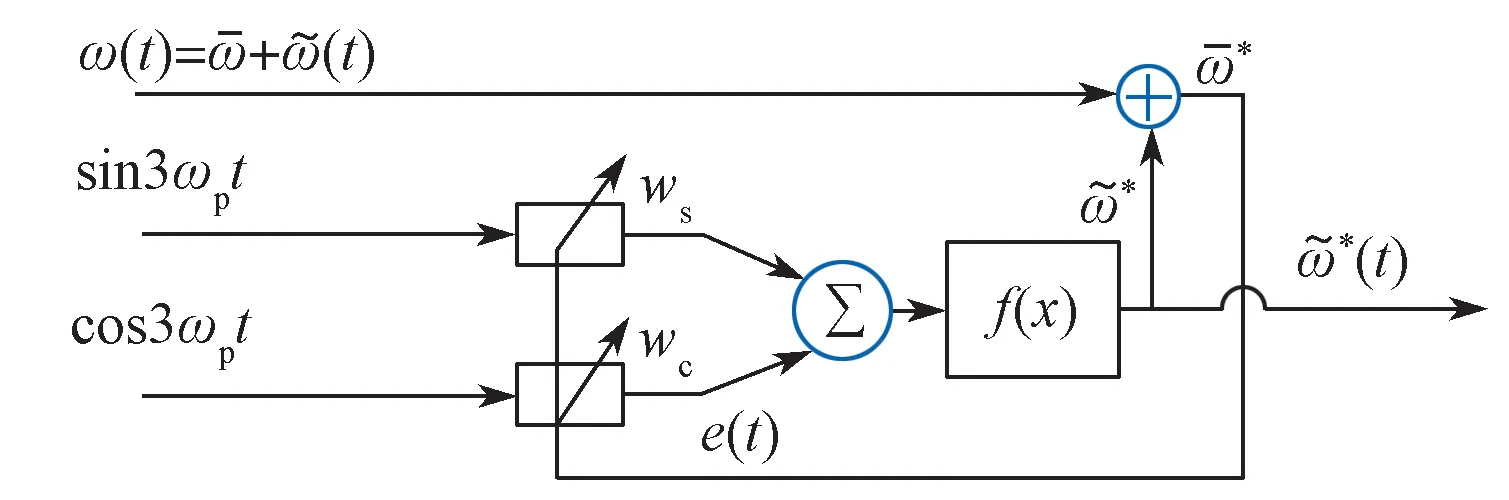
图5 ANN 自适应转速波动检测示意图Fig. 5 Schematic diagram of the speed fluctuater detecter by adaptive ANN

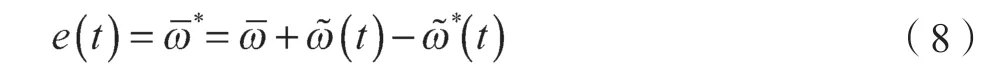
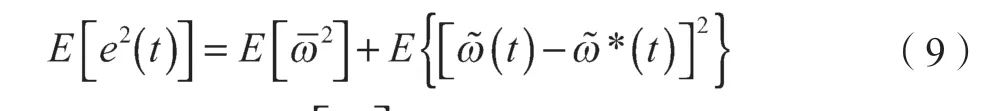
3.2 神经元学习算法

由图5 可知，单神经元模型可作为一个多输入单输出的处理元件。

输入矢量：

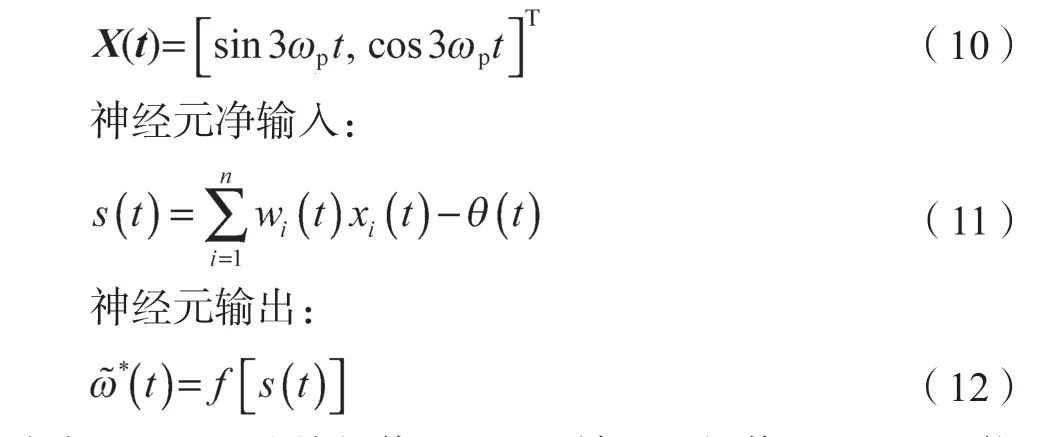
式中：wi——连接权值；θ ——神经元阈值；f(x)——激活函数。

神经元学习采用最小均方（LMS）算法e(t)来调节权值w：

式中：η——学习率，0＜η ≤1（η 取值太大，影响学习的稳定性；取值太小，会使收敛速度过慢）；含α 的项为惯性项，其可以加快收敛速度，0＜α ≤1 。

经过若干次迭代，E[e2(t)]逐渐趋向于最小值，权值逼近最优值，完成纹波信号的动态检测。

3.3 输出转矩波动软测量

电磁侧电流纹波的检测原理同上，即式（6）～式（15），检测出定子q 轴电流3 倍频纹波，定子q 轴电流可以表示为

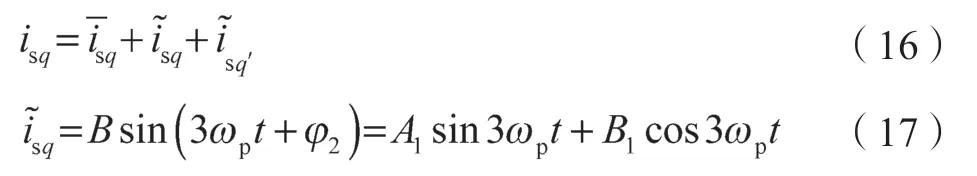
风剪切效应软测量方法，输入量为发电机定子电流和风轮转速，转速经过锁相倍频器得到正弦和余弦信号，以此作为ANN 参考输入项；转速和定子电流信号作为ANN 原始输入项，经过ANN 自适应噪声对消检测电路，得到定子电流纹波和转速波动，对这两个波动量作约束计算，可观测到输出转矩波动，具体流程如图6 所示。

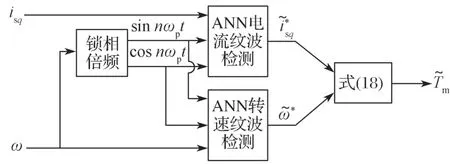
图6 风剪切效应软测量流程Fig. 6 Soft-sensing flow chart of wind shear

4 仿真验证

为了验证这种软测量方法的有效性，借助GH Bladed 平台，搭建了功率为2 MW，ωref=1.5 rad/s，ηp=30 的受风剪切影响的直驱永磁同步风力发电机并网模型，分别在转速环、定子电流环增加ANN 纹波检测网络，对转速波动和定子q 轴电流纹波进行检测，然后经过约束计算模块观测输出转矩波动。

在仿真中，ANN 初始权值和阈值为零，参考输入中的基准频率，仿真时间为10 s。转速及检测出的波动波形如图7 所示，转速波动检测过程中，多次调整学习率η 并在3 s 内完成跟踪，准确检测出转速波动的3 倍频波动含量。定子q 轴电流及检测出的纹波波形如图8 所示，尽管定子q 轴电流含有较多的高次谐波分量，ANN自适应学习算法在1～2 s 内完成收敛，输出了逼近于定子电流3 倍频纹波含量的信号。上述两项波动量经过约束计算观测到输出转矩波动波形，与输出转矩作差后得到幅值变化很小，近似于稳定分量的波形（图9），表明观测到的输出转矩波动和输出转矩3 倍频波动分量几乎没有相位差，幅值误差1%左右。上述仿真分析表明，在合适的学习率的情况下，这种风剪切效应软测量方法能够准确检测出风剪切在机械侧和电磁侧造成的波动，能够实时精准量化风剪切效应，为风电机组在线补偿和控制等进一步的相关研究奠定科学有效的基础。

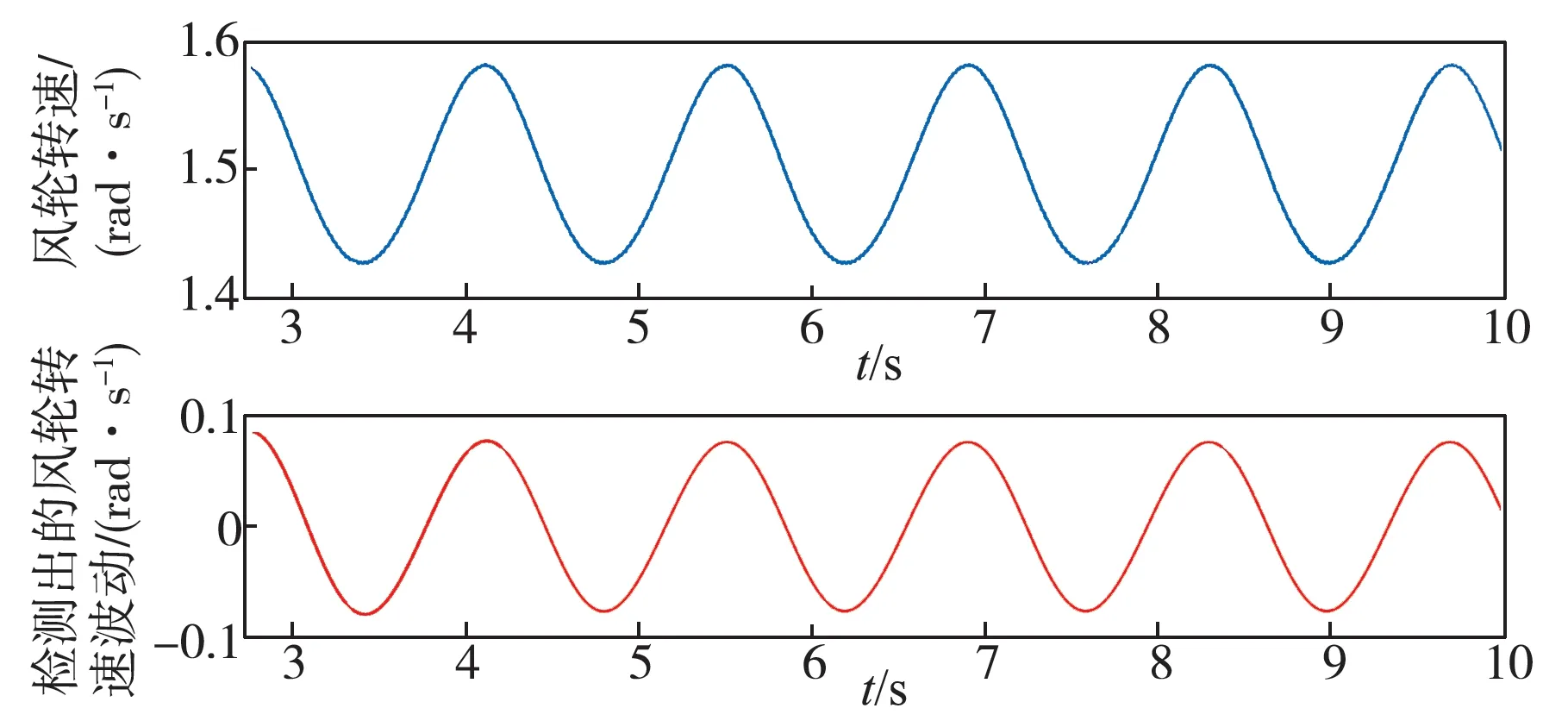
图7 风轮转速波形和检测出的波动含量波形Fig. 7 Speed waveform and measured fluctuation waveform

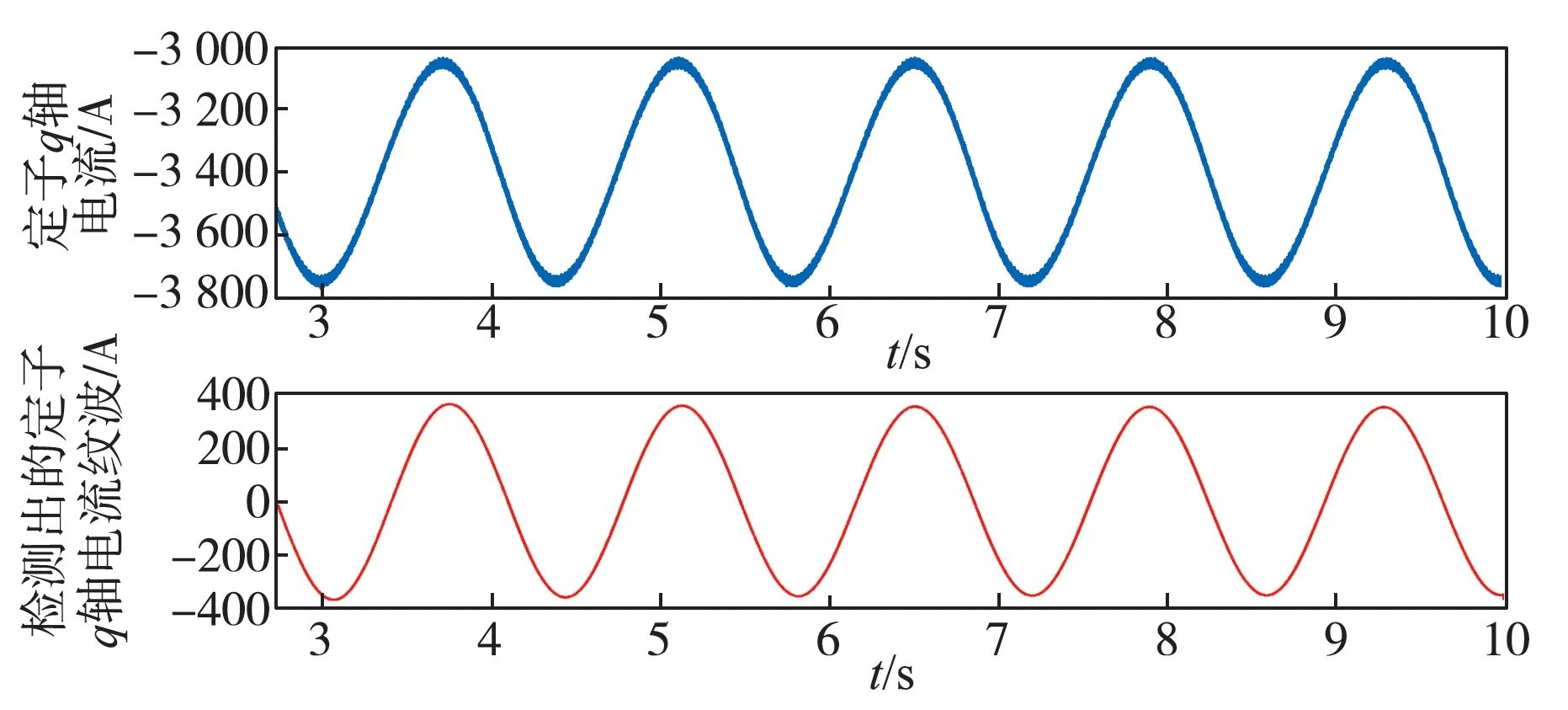
图8 定子q 轴电流波形和检测出的波动含量波形Fig. 8 Stator q-axis current waveform and measured fluctuation waveform

图9 输出转矩波形和检测出的波动含量及其作差波形Fig. 9 Output torque waveform,measured fluctuation waveform and difference waveform

5 结语

本文根据自适应噪声对消原理和单神经元的特性，结合检测的实时性要求，提出了一种基于ANN 的大型直驱风电机组风剪切效应软测量方法。其系统拓扑结构简单，应用灵活，响应速度快。仿真研究表明，这种软测量方法能在线实时测量出风剪切下风轮输出转矩波动，而且具有很高的精度，特别适用于桨叶长、塔筒高的大型风力发电机，解决了风剪切效应难以量化的难题，为延长设备使用寿命、抑制风电并网电压波动提供了研究基础。由于实际工程对波动检测有更高的动态要求，文中运用的ANN 信号检测方法由单个神经元组成，动态性能和自适应性有限，在后续的研究中将考虑采用多级神经元学习算法，进一步提高测量方法的实时性和准确度。