带广义积分边值条件的分数阶朗之万方程的解①
商启发, 周宗福
(安徽大学数学科学学院,安徽 合肥 230601)
0 引 言
分数阶微分方程是由整数阶微分方程演变而来的,能够处理整数阶微分方程无法解决的问题。分数阶微分方程在许多科学领域有着重要的运用,例如: 数学建模、物理、化学、生物技术、光学、热学和信号处理等。因此分数阶微分方程变得越来越重要,引起了广大学者的关注。关于分数阶微分方程边值问题的研究已有许多优秀的成果[1-3]。朗之万方程是物理数学中的一个重要方程,是用来描述布朗运动的。近年来分数阶朗之万方程受到了许多学者的关注,关于这方面的成果可见文献[4-8]。
文献[9],研究了下列具有广义分数阶积分边值条件的分数阶朗之万方程的解的存在性问题:
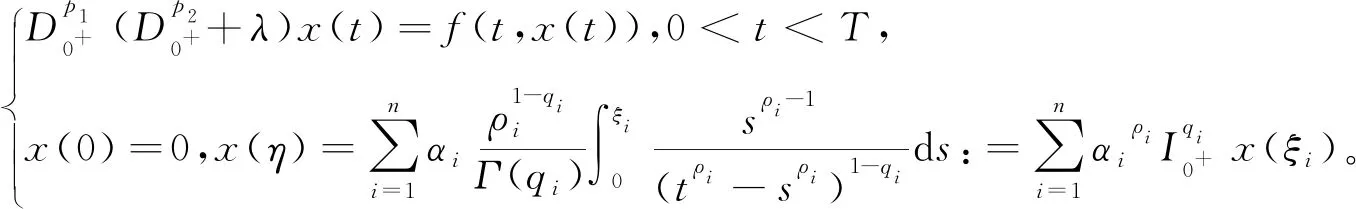
其中
文献[10],研究了下列具有非局部积分边值条件的非线性朗之万方程的解的存在性问题:
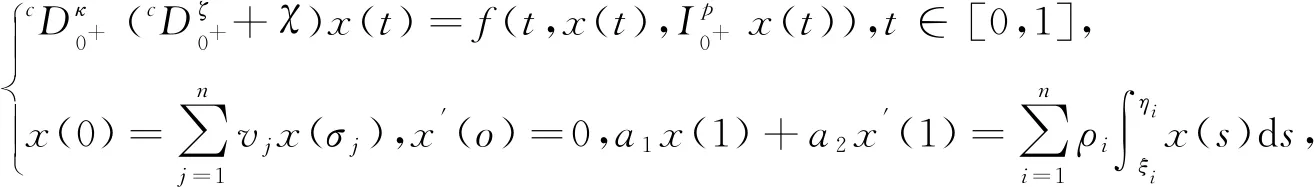
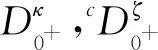
受到以上文献的启发,研究了一类分数阶朗之万微分方程的边值问题见式(1)
(1)
其中0<α≤1,1<β≤2,a,b,λi∈R且
利用Banach压缩映射原理和Leray-Schauder度理论给出了边值问题(1)解的唯一性与存在性充分性条件。
1 预备知识
定义1.1[11]连续函数f:(a,+)→R的α阶Caputo分数阶导数定义为
其中n-1<α≤n,n∈N+,Γ(·)是伽马函数。
定义1.2[11]连续函数f:(a,+)→R的α阶Caputo分数阶积分定义为
其中n-1<α≤n,n∈N+,Γ(·)是伽马函数。
引理1.3[12]如果α>0,则有
其中ci∈R,i=1,2,…,n。n为不小于α的最小整数。
为了方便起见,引入下面标记:

等价于积分方程:
(2)
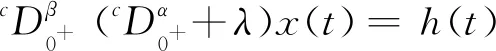
(3)
其中c0,c1,c2∈R。
从而
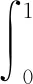
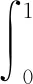
(4)

将c1代入(4),即得到(2)。证毕。
2 主要结果

定义算子T:E→E,
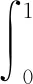
首先,利用Banach 压缩映像原理来讨论边值问题(1)解的存在唯一性。
定理2.1假设下面条件成立:
(H1) 存在L>0,使得|f(t,x,y)-f(t,x1,y1)|≤L(|x-x1|+|y-y1|),其中t∈[0,1],x,x1,y,y1∈。若
则边值问题(1)存在唯一解。
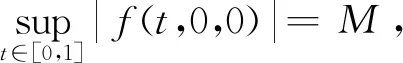
作BR={x∈E:‖x‖≤R}。下证TBR⊂BR,∀x∈BR。

对x,y∈E,t∈[0,1]
‖x-y‖+|λ|Λ(0)‖x-y‖+Ω‖x-y‖=
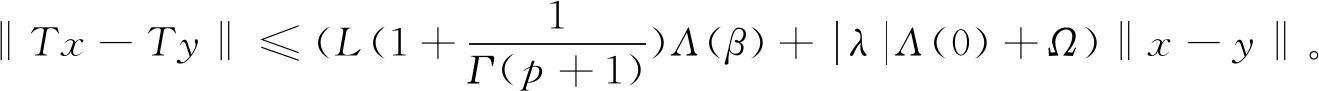
接下来利用Leray-schauder度理论来研究边值问题(1)解的存在问题。
定理2.2假设下面条件成立:
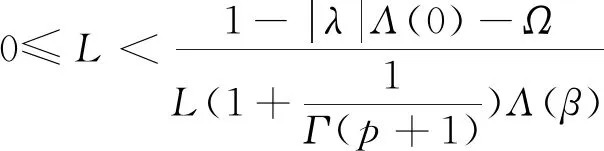
|f(t,x,y)|≤L(|x|+|y|)+M,
则边值问题(1)至少存在一个解。
证明:先证T在E是全连续的。下证T是全连续的,根据f的连续性可知T是连续的。令S={x∈E:‖x‖
|λ|rΛ(0)+rΩ。
于是TS是一致有界的。设t1,t2∈[0,1]且t1 即知,当t1→t2时,有|Tx(t2)-Tx(t1)|→0。因此TS是等度连续的。由Arzela-Ascoli定理,可知TS是列紧的,从而T在E上是全连续的。 作Bc={x∈E:‖x‖≤c,c>0},使得x≠kTx,∀x∈∂Bc,∀k∈[0,1]。令hk(x)=x-kTx,由拓扑度同伦不变性知 deg(h1,Bc,0)=deg(h0,Bc,0)=deg(I,Bc,0)=1≠0, 根据Leray-Schauder度的可解性知, h1(x)=x-Tx=0, 在Bc上至少由一个解。假设x=kTx,其中x∈∂Bc,k∈[0,1],则∀t∈[0,1],由 |x(t)|=|kTx(t)|≤|Tx(t)|≤ |λ|Λ(0)+Ω)‖x‖+MΛ(β), 从而 |λ|Λ(0)+Ω)‖x‖+MΛ(β), 因此 令 则对任意x∈∂Bc由x≠kTx并且k∈[0,1]。因此方程 h1(x)=x-Tx, 在Bc上至少由一个解,即T在Bc上至少存在一个不动点,从而边值问题(1)至少有一个解,证毕。 研究了一类带有广义分数阶积分边值条件的非线性分数阶朗之万方程解的唯一性和存在性。运用的方法是Banach压缩映像原理和 Leray-Schauder度理论。3 结 语

