软土地基上加筋挡土墙的破坏机理探讨①

张俊腾，曹文峰，袁亚芳，尤文贵，陈雪冰

(福建农业职业技术学院，福建 福州 350119)

0 引 言

软土在我国分布甚广，工程实践经常会碰到，而现有的可供设计人员参考的标准性规范关于加筋挡土墙的规定都没有考虑软土地基的影响。因此，对软土地基上的加筋挡土墙的研究具有重要的现实意义。Jewell[1]对建造在软土地基上的堤坝的破坏机理进行了研究，软土地基的剪切应力受到堤坝内部的水平压力的影响。试验结果表明，对堤坝内部进行加筋处理能够抑制水平压力的发展，进而减少软土地基的水平方向的变形。Bergado[2]在泰国曼谷软土地基上建造了一座高6m的加筋挡土墙并且进行了实测试验和数值模拟，结果显示数值模拟和实测数据较为吻合，软土地基加大了挡墙的水平位移和竖向位移。此后，Tanchaisawai[3]引用Bergado(2000)的实测数据采用Plaxis有限元软件进行了数值模拟分析。在国内，吕鹏、杨广庆[4]也对软土地基上的加筋挡土墙进行了数值模拟，研究了其变形和应力特性。目前仅陈建峰[5-6]对软土地基上柔性加筋挡土墙的剪切带进行了探讨，但是只分析了筋材长度的影响而且其破坏模式均是深层滑动。因此，在此基础上参照Tanchaisawai(2008)引用Bergado(2000)实测数据，引入HSS本构模型，重点从剪切带(破裂面位置[7])入手，进一步分析软土地基上柔性加筋挡土墙的破坏机理。

1 数值模型

1.1 模型的建立

所采用的挡墙的几何模型、施工过程、各土层参数均与Bergado[2]一致。根据试验挡墙数据：挡墙高6m，风化层厚度为2.5m，风化层下面为8.5m厚软土层，软土层下面为坚硬的砂土，筋材间距为0.5m，长度为6m，如图1。Richard[8]通过试验指出，柔性面板的加筋挡土墙的变形比刚性面板的更加显著。柔性加筋挡墙的构造区别于刚性加筋挡墙的关键在于：墙面由土工材料返向包裹，包裹长度按照《铁路路基支挡结构设计规范》2006版取2m，加筋体为弹性材料，刚度K=EA=1000 kN/m，其中E为弹性模量，A为横截面积。挡墙采用逐级填筑的方法施工，施工过程如图2。为了更好的考虑土体结的影响，采用考虑几何非线性大变形对有限元网格的影响：模拟施工过程每层固结时间为3d，总工期为36d，有限元模拟的阶段为0d-200d。

陈建峰(2012)在采用有限元软件Plaxis建模的时候除了填土和砂垫层采用M-C模型外，其余土层均采用HS[9]模型。考虑到Bergado(1995)在试验的过程当中虽然出现了挡墙和基地的较大变形，但是土体颗粒的应变很小(3%以内)，如果用破坏状态下的土体参数来反映土体在低应变状态下的力学特性显得不太合理。因此采用建立在HS基础上经过改进的HSS[10]模型，后者的参数只比前者多了两个：小应变模量和剪切应变水平。HSS模型对这两个参数极其敏感，因此准确选取这两个参数对数值模拟至关重要。这两个参数要通过现场震测和小应变三轴试验才能较为准确的获取，笔者根据经验数据：

γ0.7=0.0002

(1)

(2)

表1 各土层计算参数

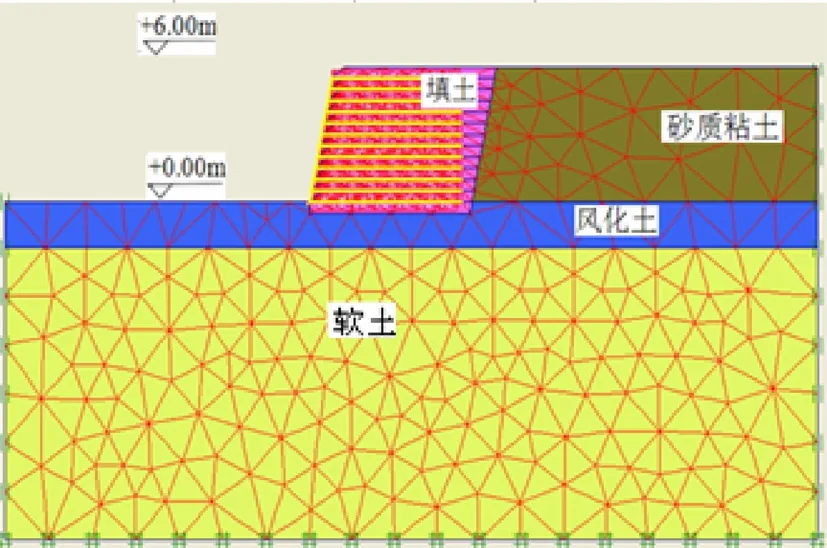
图1 挡墙的有限元模型

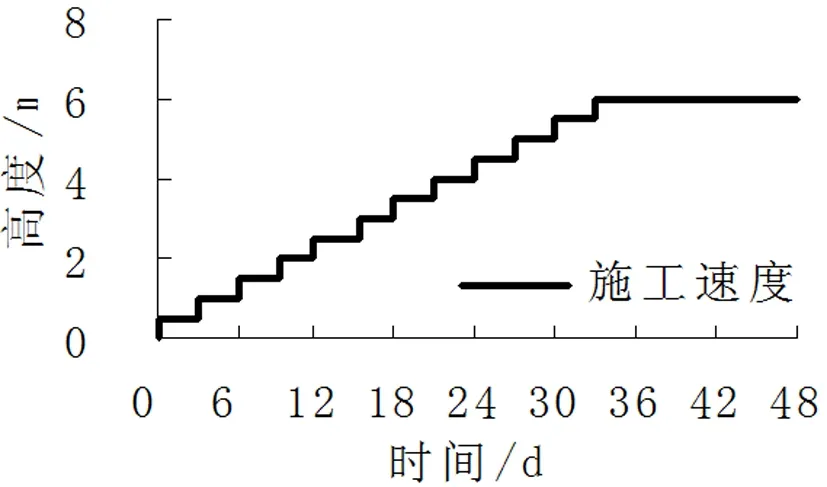
图2 有限元的施工模拟过程

1.2 计算结果比较

为了能够与实测结果值进行比较，本节的基底沉降值选取考虑土体固结至第60d的计算值。由图3可值，第60d时挡土墙基底最大值位于离墙趾6m处(墙趾坐标为0，5m)，其值约为150mm。 五年后Bergado(2000)用有限元软件进行了数值模拟，其计算结果比实测值略大但是总体规律与实测值基本吻合。采用HSS本构关系的有限元软件进行了补充计算，计算结果显示基底沉降曲线与实测值更加吻合。值得说明的是Bergado(2000)在数值建模时采用的本构关系为：填土MC(摩尔库伦)，地基土SSM(软土蠕变)。已有很多文献指出：挡墙的水平位移沿着墙身向上不断增大，沿着基底向下不断减小。Bergado(1995)的实测结果也验证了此规律。由图4可知，第126d时Bergado(2000)的有限元计算结果除了基底的水平位移与实测值相差较大外，其余基本上与实测值吻合。这可能是因为SSM模型过高的估计了基底土体的弹性范围或者是不能考虑挡墙实际施工过程受到卸载重加载的影响。采用HSS模型在计算水平位移时墙身和基底均与实测结果吻合，这说明采用HSS模型比采用SSM模型计算加筋挡土墙的结果更加准确。

Rankine,1857根据挡墙与墙背土体之间的位移关系将墙背土压力分为三种：1)主动土压力σa，2)静止土压力σo，3)被动土压力σp。三者之间的关系为：σaσoσp，具体公式如下，

(3)

σ0=γhk0

(4)

(5)

其中Ka=tan2(450-φ/2)，k0=1-sinφ′，

KP=tan2(450+φ/2)，h为挡墙高。

图3 挡墙第60d基地沉降的实测值与数值计算值

图4 挡墙中心线水平位移实测值与数值计算值

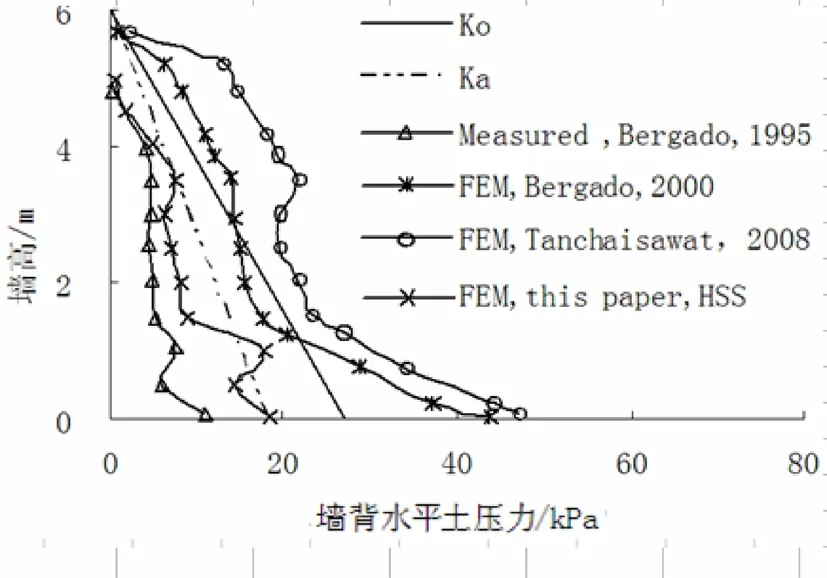
图5 挡墙墙背土压力的实测值与数值计算值

由图5可知，加筋挡土墙的墙背土压力实测值比主动土压力小很多，说明加筋能够有效抑制挡墙内部应力的发展。Bergado(2000)的有限元计算值比实测值略大总体上分布在主动土压力线附近。采用HSS模型计算的土压力值分布在静止土压力线附近，比前者更加接近实测值。有趣的是Tanchaisawai (2008)也采用SSM模型进行了数值模拟，但是他的土压力计算值比实测值大很多，其数值甚至分布在静止土压力线外。这可能是Tanchaisawai (2008)缺乏更详细的试验资料，因此建模时没能很好的选取计算参数。

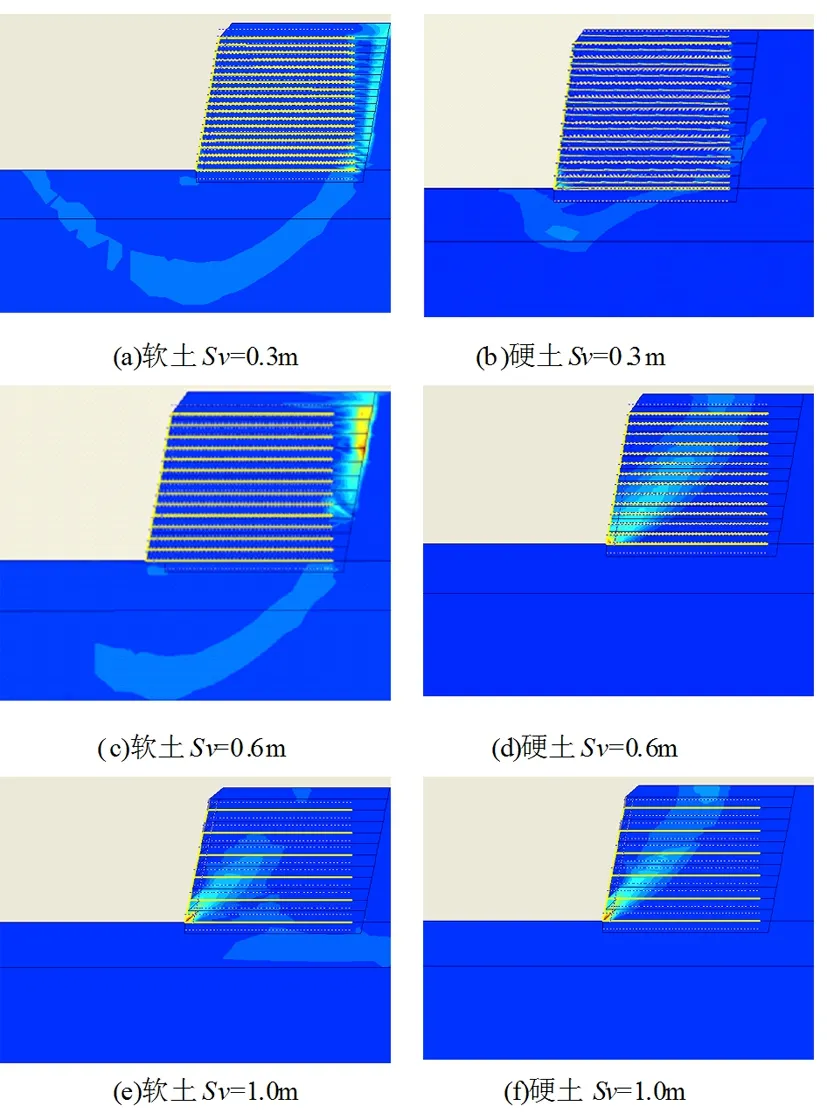
图6 不同加筋体间距Sv加筋挡土墙的剪切带

2 结果分析与讨论

2.1 加筋体间距影响分析

为了更好的分析软土地基对加筋挡土墙的影响，采用坚硬土地基与之对比。硬土层的内聚力取30 kPa，内摩擦角取30，另外硬土层的压缩模量取20000 kPa，其余参数参照软土层。

图6中的(b) 、(d)、 (f)为硬土柔性加筋挡土墙的剪切带，不难看出加筋体间距Sv=0.3m时挡墙发生滑移破坏，Sv=0.6m和1.0m挡墙发生倾覆破坏。说明，加筋体间距过大的话则不能形成形成一个有效的筋土组合体。对于硬土上的挡墙，发生倾覆破坏时破裂面始终在传统0.3H法确定的范围内。再比较软土地基上的剪切带位置，当加筋体间距为Sv=0.3m和Sv=0.6m挡墙处于深层滑动破坏状态，而当加筋体间距Sv=1.0m时挡墙的剪切带位置与硬土的一样出口位于墙趾，如图6(a) 、(c)、 (e) 、 所示。这说明，软土地基上的加筋挡土墙受加筋体间距影响既有可能发生倾覆破坏也可能发生深层滑动破坏。倘若用摩擦加筋原理来解释筋土组合体的稳定性的话：填土够密实和加筋体间距足够使加筋体上下层的土体能够传递其摩阻力和法向应力，从而形成一个能够与土压力相抵消的“承压拱”。至于破坏模式是前者还是后者，主要取决于挡墙的筋土组合体的稳定性与地基土的相对稳定性。

2.2 加筋体长度影响分析

在加筋间距不变的情况下通过改变加筋体长度同样可以改变筋土组合体的内摩擦力，从而改变筋土组合体的稳定性。如图7(a) 、(b)，当加筋体长度L=0.4H时挡墙不能形成有效的筋土组合体，这时挡墙只能靠土体自身的强度来维持其稳定性，使得倾覆破坏先于滑移破坏发生。如图7(c) 、(d)，当加筋体长度L=0.9H时，软土地基上的挡墙发生深层滑动破坏，硬土地基上挡墙依旧发生滑移破坏。如图7(e) 、(f)，当加筋体长度L=1.2H时，软土地基上的挡墙发生深层滑动破坏，硬土地基上挡墙发生滑移破坏。这说明了，对于软土地基上的加筋挡土墙当加筋体长度较大时，深层滑动破坏先于倾覆破坏发生，当加筋体长度较小时则发生倾覆破坏的趋势，而且破裂面的位置已经超出了《铁路路基支挡结构设计规范》2006规定的加筋体最小长度0.8h的范围，如图7(a)(c)(e)所示。

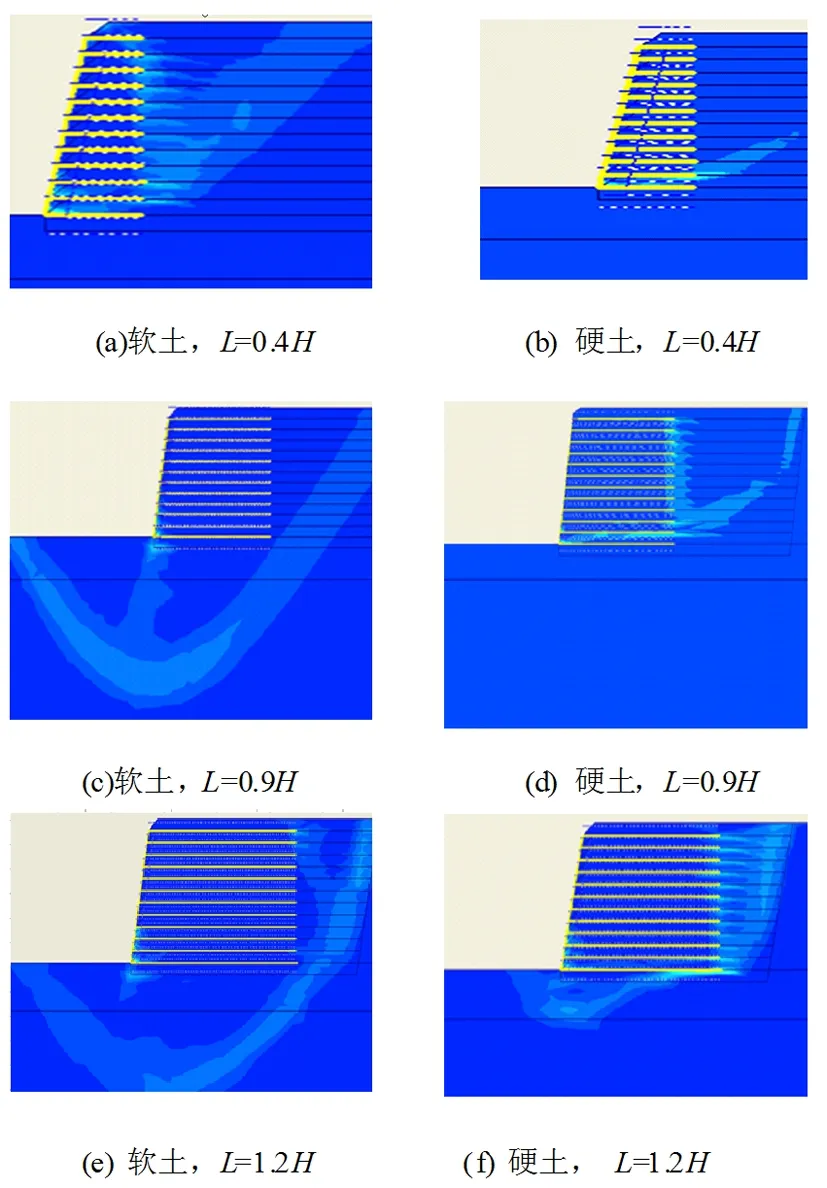
图7 不同挡墙厚度加筋挡土墙的剪切带

2.3 地基土强度影响分析

现有的规范计算边坡和挡墙的稳定性所采用的公式大多是基于极限平衡法和解析法推导而来。其原理是预先假定一个滑动面，然后将滑动面以上的土体划分成有限个小刚体再计算安全系数，然后重复以上步骤多次，最后找出最小安全系数和所对应的滑动面。采用有限法分析稳定性所采用的方法是强度折减法。

如图8(a)(b)(c)所示，地基土的内摩擦角为不变，而内聚力从15 kPa减少到10kPa时其剪切带均从墙顶的加筋体末梢剪入，而从距墙趾h远处剪出呈弧形性状，属于典型的深层滑动破坏。不同的是，其剪切带的宽度和深度呈逐渐加大的趋势。如图8(d)(e)，保持内聚力为10kPa不变，继续减小内摩擦角，除了原有的剪切带加大外，还有另外一个剪切带开始从墙趾往下发展并与前者汇合呈“锚形”性状。继续减小地基土的强度，第三条剪切带也随之出现，如图8(f)。这时候的地基根本无法承载力挡墙的重量，所以才会呈地基整体失稳破坏的趋势。说明了采用强度折减法分析挡墙的稳定性更加贴近实际。

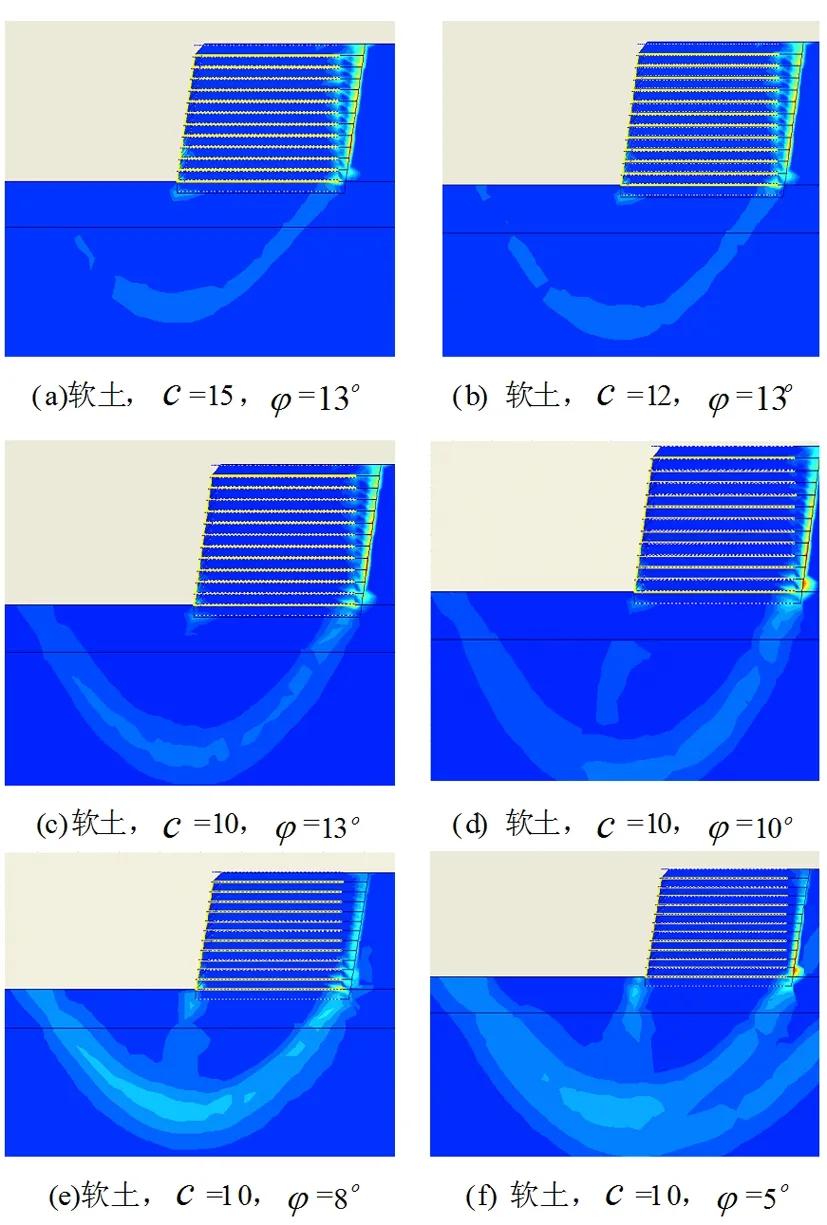
图8 不同地基土强度加筋挡土墙的剪切带

3 结 语

通过数值模拟软土地基上柔性加筋挡土墙的性能特性得出一下结论：

(1)采用HSS本构模型分析软土地基上加筋挡土墙的工作性状比HS和SSM本构模型更准确。

(2)采用强度折减法分析软土地基上加筋挡土墙的稳定性更加贴近实际。

(3)软土地基上加筋挡土墙的破坏模式不但受加筋体长度的影响，还受加筋体间距、加筋体长度和地基土强度等因素的影响。其破坏模式有可能是倾覆破坏，也可能是深层滑动破坏，甚至是地基整体失稳破坏。挡墙先破坏还是地基先破坏主要取决于筋土组合体与地基土的相对稳定性。

(4)在设计软土地基上的柔性加筋挡土墙墙时，设计人员不可生搬硬套规范，应该综合考虑多种因素的影响，并且采用有限元软件进行补充计算。对于重要工程更应该采用两种以上不同力学模型的有限元软件仔细分析。