九相感应电机切套运行的非线性磁路计算

李永佳，郑晓钦

(青岛大学 电气工程学院，青岛 266071)

0 引 言

推进系统是舰船综合电力系统最重要的组成部分之一，而推进电机又是推进系统的核心，其重要性显而易见[1]。高可靠性是对推进电机最基本的要求，同时，效率、功率密度、容错能力、适用范围等也是推进电机必须考虑的考量标准[2-3]。多相感应电机结构简单、运行可靠，变频器供电模式下又可以克服电网供电的诸多弊端，已成为舰船选择推进电机时的首选。

为确保电机的高可靠性指标，多相感应推进电机设计时通常以一套三相或五相对称绕组为基本单元，几套基本单元共同构成电机所有绕组，每套基本单元通过控制器可实现自由投入、切出运行，实现低压大功率的驱动策略[4-5]。此外，多套多相的设计结构还使得电机某一相发生故障时可以主动切出故障绕组所在的整套绕组，电机转而工作在切套工况，既可以简化容错控制方式，又可以使电机其余各套绕组受到故障影响降到最低，从而保证推进系统的可靠性[6-9]。

多相感应电机在缺相故障工况下特有的切套运行性能对评估推进系统可靠性极为重要。大容量多相感应电机正常运行性能分析需要考虑铁磁材料的饱和因素影响，而多套多相绕组投入切出运行时饱和程度会随之改变。因此，为精确分析多套多相感应推进电机不同套数绕组投切时的运行性能，必须根据绕组具体套数投切情况，重新对切套运行的磁路进行计算。目前,常用的磁路分析方法主要有解析磁路法[10-11]、磁网络法[12]、有限元法[13-15]和分布磁路法[16-17]。解析磁路法是以磁动势计算为基础，通过转差率及各种系数的循环迭代计算，最终求得气隙磁通密度最大值。该方法优点在于思路清楚，易于理解，缺点在于计算过程过于依赖经验系数、饱和系数进行修正，影响了磁动势计算的准确性。磁网络法的计算基础是磁网络，在电机模型中磁网络由等效磁动势源和等效磁阻构成，并由此建立磁动势计算方程，求解方程得到气隙磁密的分布情况。该方法应用时可以充分考虑齿槽效应与饱和效应的变化影响，但是磁网络模型复杂不易理解，建立难度大，缺乏通用性。有限元法将电机模型划分为很多小的子域，建立基于磁场中各种定理、条件的方程等限制条件求数值解。该方法优点在于有限元模型可以考虑齿槽效应等因素的影响，计算精度较高，缺点在于有限元法计算过程复杂，花费时间长。分布磁路法是以基波磁动势为计算基础，将电机模型进行分块，气隙中心线处对应多个节点，根据节点处的磁势迭代计算得到每个节点处的气隙磁密。分布磁路法从根本上取消了修正系数，避免了修正系数对计算结果的影响，此外还有计算速度快、精度高、适用范围广等许多优点。

针对九相感应电机切套运行的特殊工况，本文采用分布磁路法计算具体套数绕组切出时的磁路，得到反映切套前后三种工况下磁路变化的具体数组，拟合得到相应的励磁电流、励磁电感之间的非线性关系曲线，利用有限元仿真方法验证了本文分布磁路法磁路计算的正确性。

1 九相感应电机绕组结构

本文研究的九相感应电机绕组构成为三套三相开端绕组，每套绕组三相间相差2π/3电角度，每两套三相绕组偏移π/9电角度，构成中性点独立的半对称绕组结构。当发生缺相故障需切套运行时电机共有三种运行状态，即三套三相绕组运行、两套三相绕组运行、一套三相绕组运行。图1分别给出三种运行状态下的绕组变化情况。

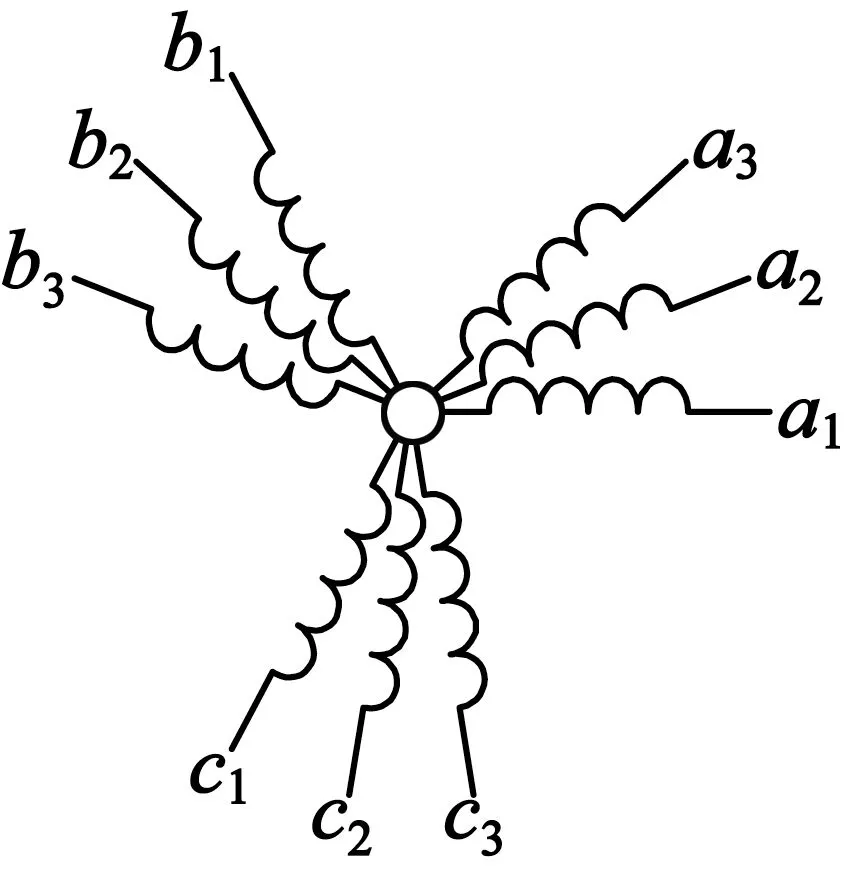
(a)三套绕组

2 分布磁路法计算过程

分布磁路法是一种对多个磁回路进行迭代计算的数值方法，对计算区域进行等间隔周向分块处理，根据处理后气隙中心线各节点处的磁势迭代，求得各节点磁密，进而计算励磁电感。

九相感应电机正常运行时，基波励磁电流产生的基波磁势幅值：

(1)

式中：W为每相串联总匝数；kw1为基波绕组系数；p为极对数；Im为基波励磁电流有效值。

2.1 磁路模型的建立

对于九相感应电机，由于磁场在同一个磁极内为偶对称，相对的磁极为奇对称，因此应用分布磁路法计算九相感应电机磁路时不需要计算整个区域，只计算1/2个极距即可。周向用通过圆心的N+1条射线将磁路模型等间隔分为N块，径向分为5个区域，分别为转子轭部区(Ⅰ)、转子齿部区(Ⅱ)、气隙区(Ⅲ)、定子齿部区(Ⅳ)、定子轭部区(Ⅴ)，如图2所示。

2.2 气隙磁密的确定

在计算气隙磁密的实际值时，首先给定励磁电流Im初值，则第i节点的气隙磁动势可表示：

(2)

第i节点处的气隙磁密：

(3)

式中：ge为考虑齿槽效应后的等效气隙长度；kst为预取饱和系数；μ0为空气磁导率。

若已知所有节点处的气隙磁密Bg(i)(i=1，2，…，N+1)，根据磁通连续性原理，可求得所有节点处的定、转子齿部磁密Bt1(i)，Bt2(i)，定、转子轭部磁密Bc1(i)，Bc2(i)。对应的磁场强度Ht1(i)，Ht2(i)，Hc1(i)，Hc2(i)可以通过查定、转子铁心材料的磁化曲线得到。

图2中加粗黑实线所围回路即为经过第i节点的磁回路，求该磁回路的磁压降，分析可知,其由五部分构成，分别为第i节点处的气隙磁压降Fg(i)，第i节点至第N+1节点间的定、转子齿部磁压降Ft1(i)，Ft2(i)，第i节点至第N+1节点间的定、转子轭部磁压降Fc1(i),Fc2(i)。五部分的值分别如下：

(4)

Ft1(i)=Ht1(i)ht1

(5)

Ft2(i)=Ht2(i)ht2

(6)

(7)

(8)

式中：ht1，ht2分别为定、转子齿高；lc1，lc2分别为定、转子一个极的轭部长度。

闭合回路总磁压降:

FΣ(i)=Fg(i)+Ft1(i)+Ft2(i)+Fc1(i)+Fc2(i)

(9)

闭合回路总磁压降应等于i点的气隙磁磁势，即式(9)应等于式(2)。由于迭代是针对所有节点进行的，故采用式(10)来作为两部分相等的判别公式。

(10)

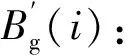
(11)

式中：kb为经验系数，取值范围为0.05～0.5。

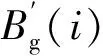
2.3 励磁电抗的确定

当气隙基波磁密幅值Bgm已知时，即可求得每极磁通最大值Φm：

(12)

励磁电感的值：

(13)

3 九相感应电机切套运行磁路计算

对九相感应电机进行磁路计算时，首先确定一个励磁电流的工作范围，对励磁电流值以一定的数值间隔累加，直到覆盖整个工作范围。每改变一次励磁电流值，则重新进行一次气隙磁密和励磁电感的计算过程，得到一组反映励磁电流与励磁电感关系的二维数组。当九相感应电机发生缺相故障时，可以主动切出这一相绕组所在的一套三相绕组，这时电机工作在对称缺相工况下。磁路非线性时励磁电抗计算流程图如图3所示。

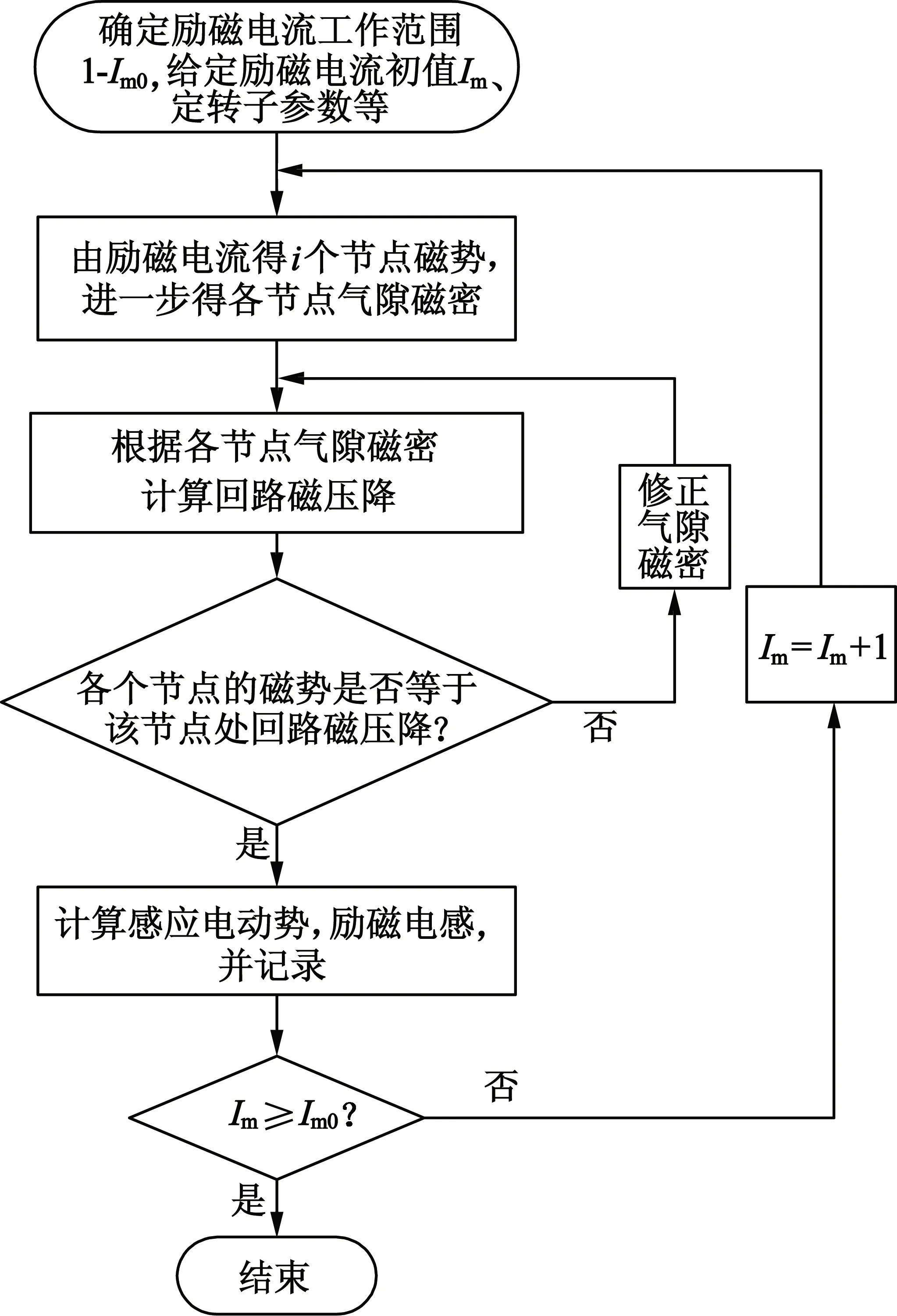
图3 磁路非线性时励磁电感的计算流程

将磁路计算得到的数据进行拟合，即可得到此时磁路的非线性关系曲线。九相感应电机正常运行时的非线性曲线如图4所示。九相感应电机切套运行又可以分为切出一套绕组运行和切出两套绕组运行两种工况，对应的励磁电流与励磁电感关系曲线如图5、图6所示。

图4 九相感应电机全绕组运行

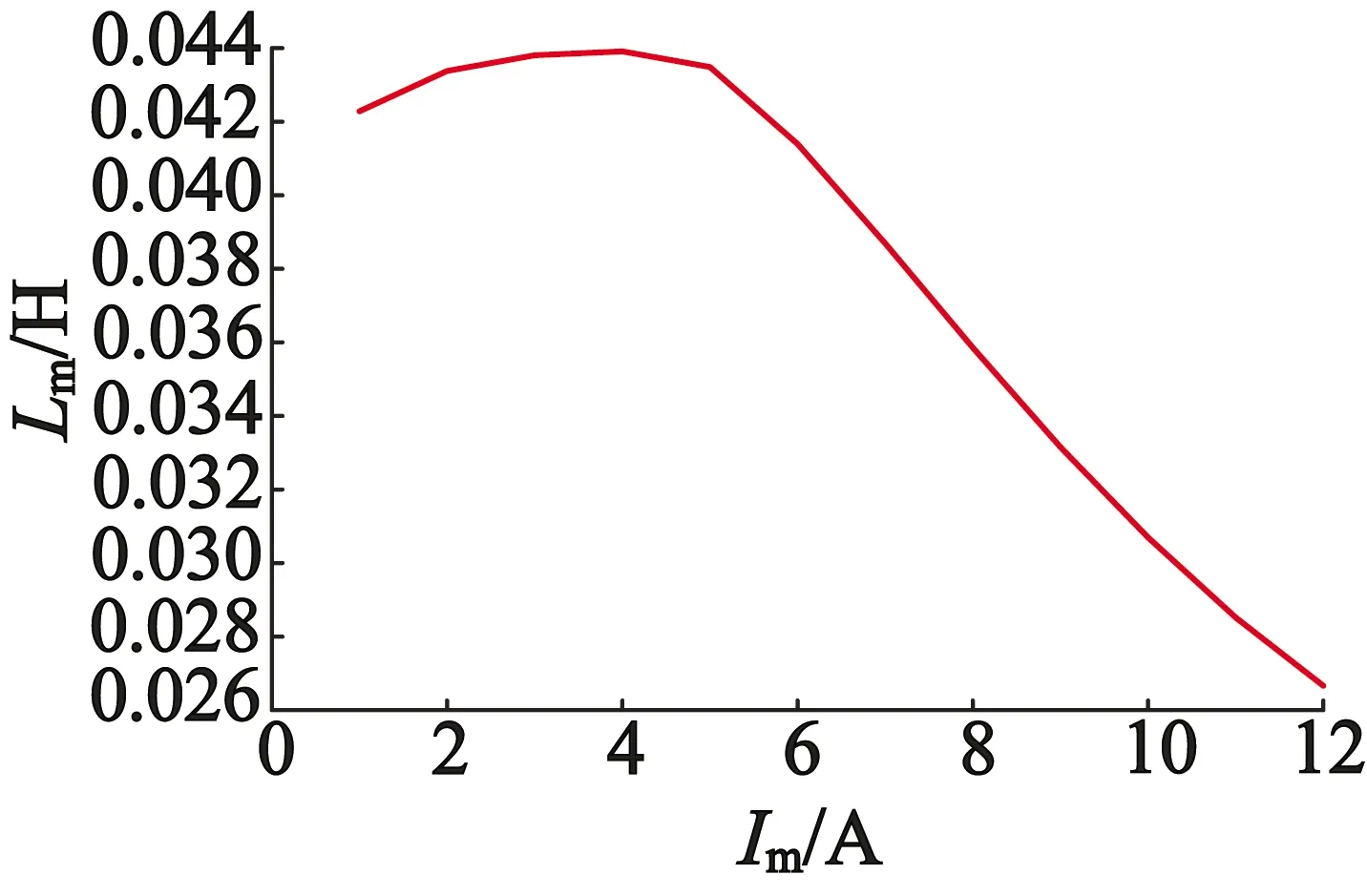
图5 九相感应电机切出一套绕组运行

图6 九相感应电机切出两套绕组运行

4 有限元验证

为验证分布磁路法计算结果的正确性，建立九相感应电机有限元模型进行仿真，电机参数及仿真模型如表1和图7所示。

表1 8 kW九相感应电机主要参数

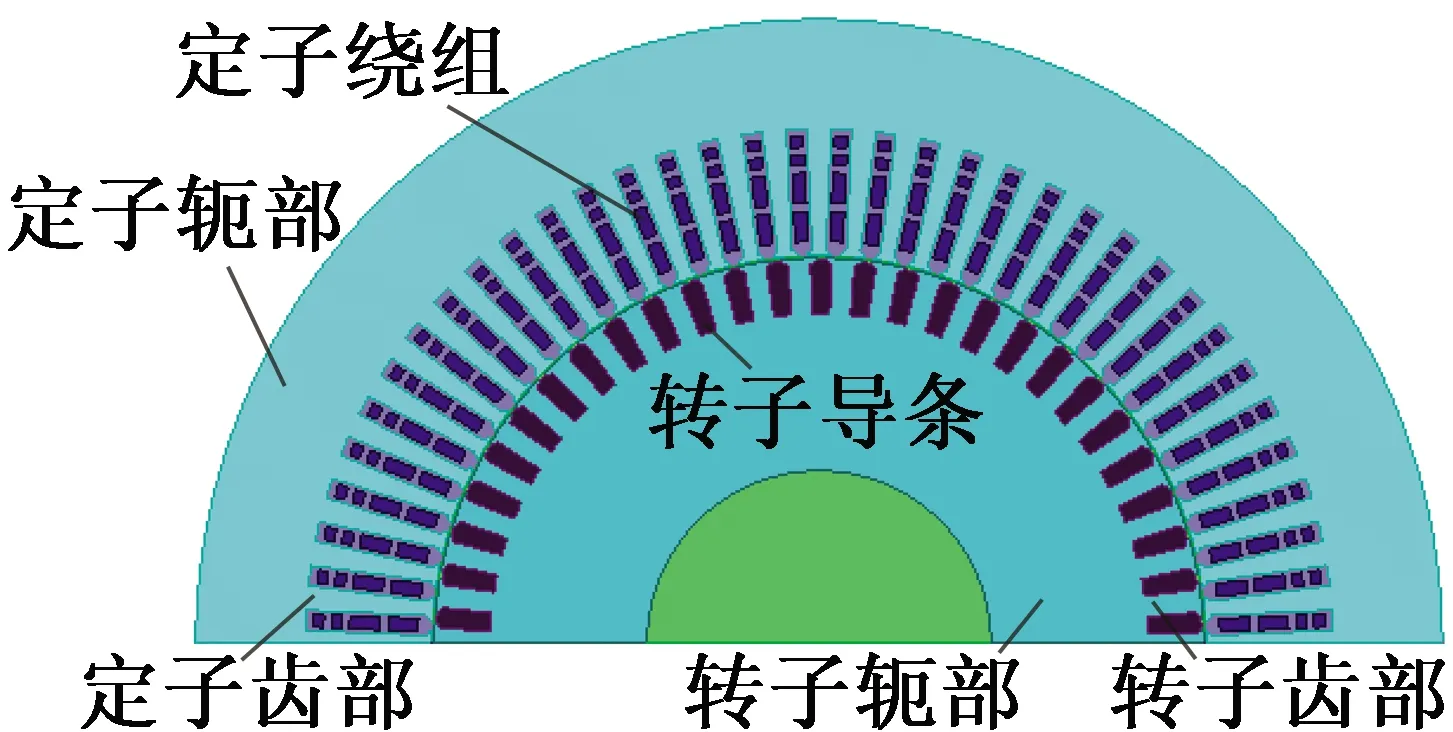
图7 8 kW九相感应电动机有限元模型

对九相感应电机进行空载运行仿真，其定子电流即为励磁电流。选取电机运行稳定后几个周期的定子电流、电压数据，利用傅里叶分解程序对其进行处理后得到定子基波电流、电压的幅值和相位，根据式(14)可以求出相应的励磁电抗。

(14)

式中：Xm为励磁电抗；U，φU分别为某一相电压的幅值和相位；I，φI分别为某一相电流的幅值和相位。

为避免偶然性，减小仿真误差，取三组定子电压、电流值分别进行处理计算，认为三组励磁电抗的算术平均值为励磁电抗仿真值。利用有限元软件分别仿真九相感应电机三套三相绕组全部正常运行、切出一套三相绕组运行以及切出两套三相绕组运行时的磁路变化情况，并计算对应工况下励磁电感，与磁路法计算结果进行对比验证，三种工况下的磁力线分布图如图8～图10所示，对应的磁路法与仿真法对比验证如表2～表4所示，误差计算以仿真值为基准。

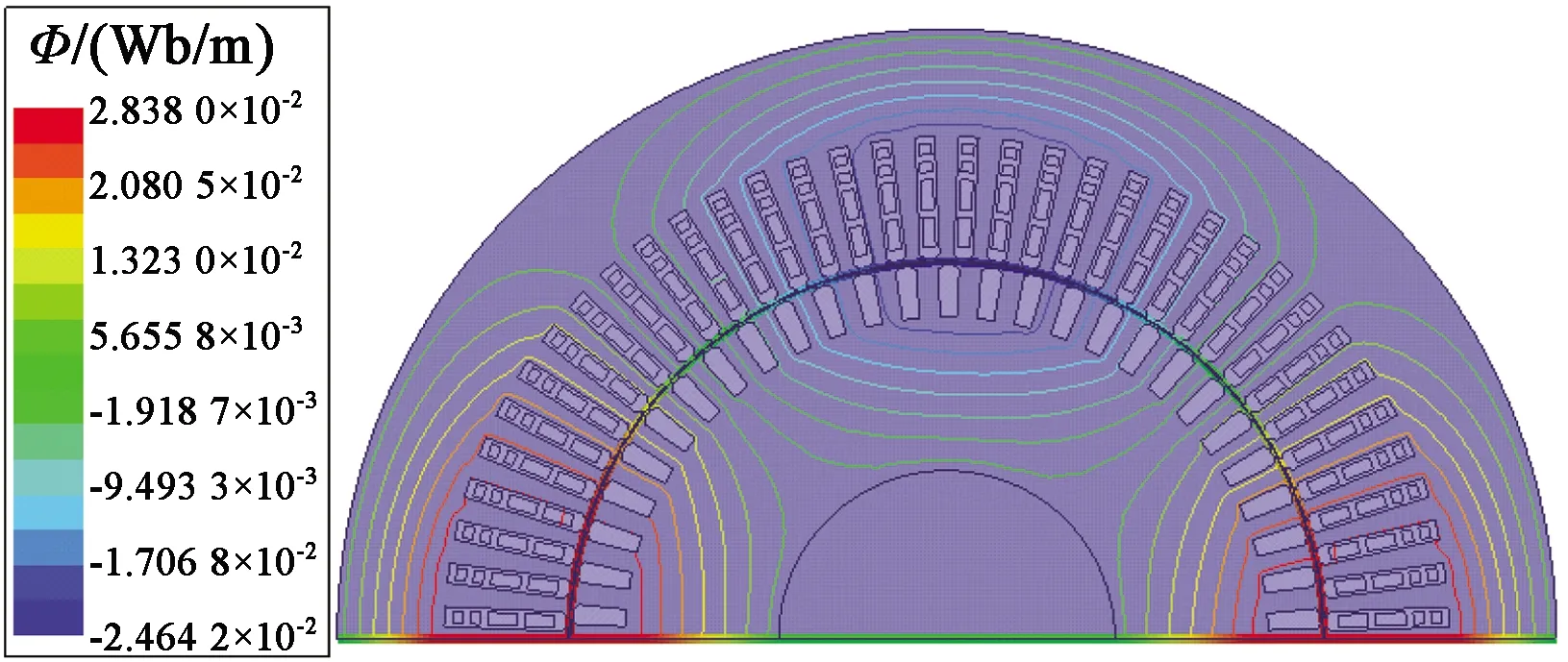
图8 九相感应电机正常运行磁力线分布图

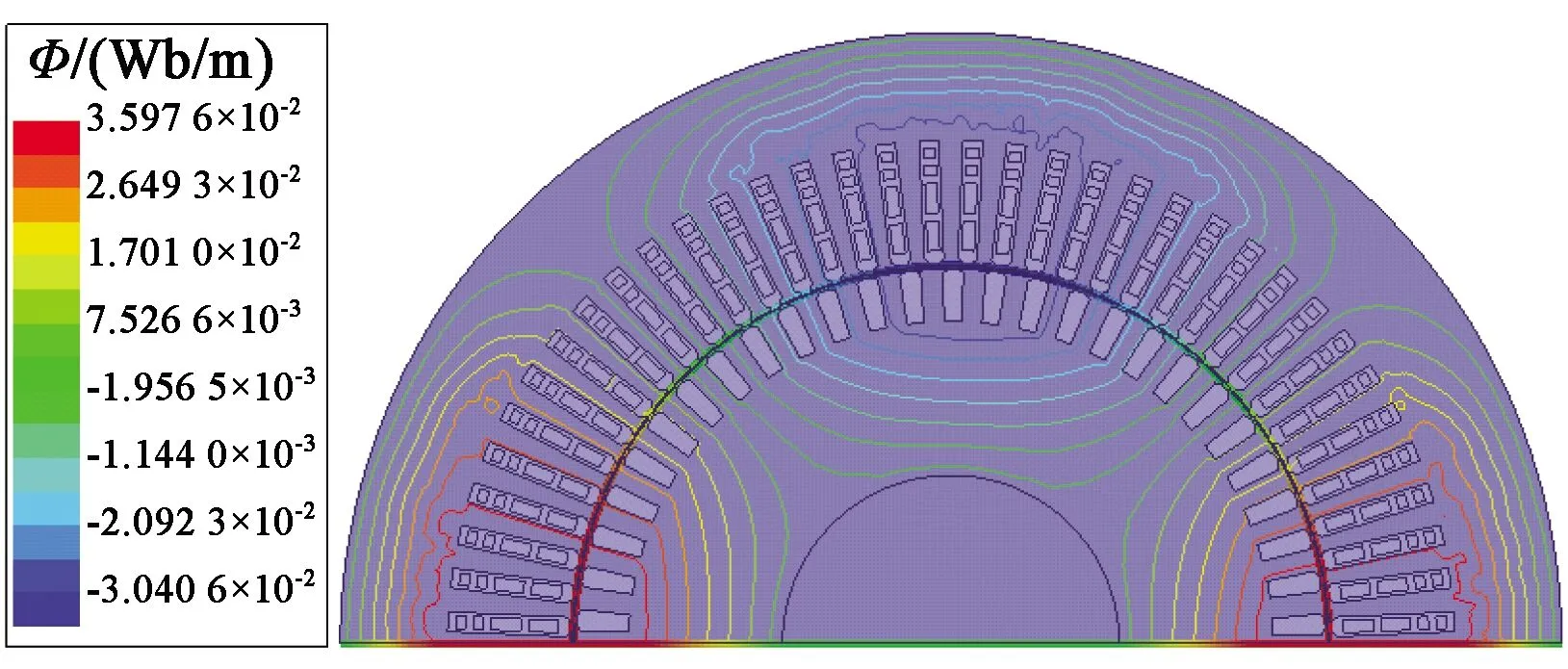
图9 九相感应电机切出一套绕组运行磁力线分布图

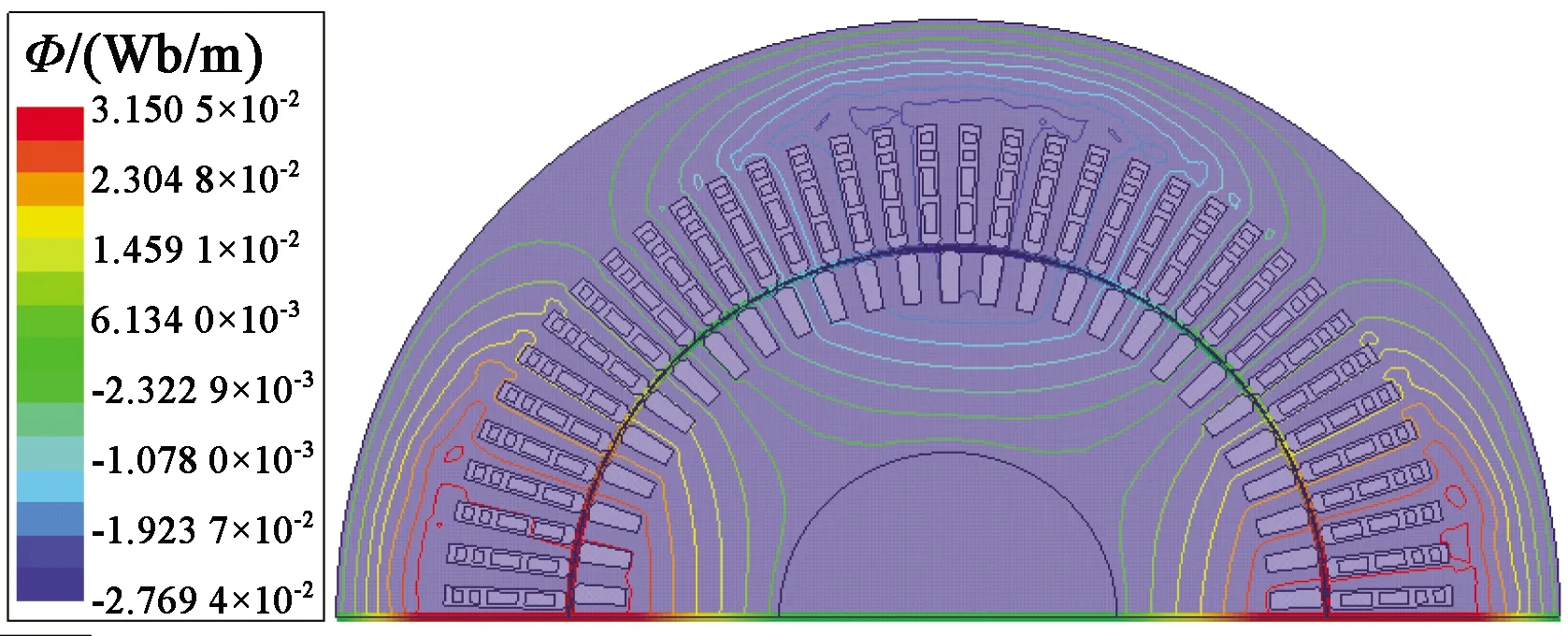
图10 九相感应电机切出二套绕组运行磁力线分布

由表2～表4可以看出，有限元仿真结果与分布磁路法的非线性计算结果吻合度较高，误差约在5%以内。造成误差的主要原因是分布磁路法与仿真计算漏阻抗存在差异，电压等级越低，漏阻抗在磁路中占比越大，所引起的误差越大。

表2 正常运行计算值与仿真值对比

表3 切出一套绕组运行计算值与仿真值对比

表4 切出两套绕组计算值与仿真值对比

5 结 语

本文以一台三套三相绕组构成的九相感应电机为研究对象，研究了多套多相绕组结构的感应电机在正常运行工况及切出不同套数绕组运行工况下的磁路饱和特性变化情况，得到了三种工况下励磁电流与励磁电感的非线性关系曲线，任意励磁电流下对应的励磁电感可直接进行非线性插值求取。在曲线达到顶点前电机工作在不饱和区，励磁电感随励磁电流的增大而增大。顶点之后电机磁路达到饱和状态，电机工作在饱和区，励磁电感随励磁电流的增大而减小。

利用有限元软件进行了九相感应电机正常运行与切出一套、两套绕组运行三种工况下的磁路仿真，对分布磁路法的计算结果进行了验证，仿真结果与计及磁路饱和时的非线性计算结果较为吻合，验证了九相感应电机磁路的非线性，为掌握九相感应电机切套工况下的电机性能指标打下了基础。